基于能量法的独塔斜拉桥施工索力优化研究

2021-07-22金俊杰

湖南交通科技 2021年2期

金俊杰，沈勇

(湖南省交通建设工程监理有限公司，湖南长沙 410015)

独塔斜拉桥一般适用于跨径较小的斜拉桥，其结构特点为刚构体系，主梁可采用多种截面形式，相比于大跨径多塔斜拉桥，独塔斜拉桥非线性效应不明显，刚度更大，内力和挠度控制简单，是一种连续梁桥的常见改良形式，在我国桥梁建设中得到了广泛应用。在独塔斜拉桥中，索力控制至关重要，它决定了斜拉桥成桥后的内力和刚度分布。目前已有众多学者开展了独塔斜拉桥的研究，韩伟[1]以某铁路独塔斜拉桥为工程背景，基于无应力状态法对斜拉桥成桥索力进行了研究；李鸿波等[2]将粒子群算法成功应用于某矮塔斜拉桥索力调整中，并取得了良好的效果；孙全胜等[3]以主梁和主塔运营阶段内力为目标，研究了斜拉索张拉方案与张拉次数对斜拉桥主梁内力的影响；孙平宽等[4]研究了索力与合理成桥状态之间的影响，确定了合理索力的调整方法。

大量研究成果表明：斜拉索索力优化方法众多，不同优化方法得到的合理索力值也并不完全相同。目前在独塔斜拉桥索力调整中，应力平衡法以及影响矩阵法占据了主导地位，两种优化方法的精度较高。但是索力调整过程繁杂，需要对每个施工阶段进行正装迭代求解，计算量庞大，而能量法则能有效避免以上两种方法的短板，以主梁弯曲应变能为优化目标可有效避免复杂的计算过程，大幅提高计算效率。本文以某独塔斜拉桥为工程背景，基于能量法对斜拉索施工期索力进行了优化，研究成果可为该类工程调索提供参考。

1 工程概况及有限元建模

某双跨不对称独塔斜拉桥，墩塔梁固结。设计荷载等级为公路 — Ⅰ级，桥跨布置为(102+130)m，斜拉桥主梁为预应力混凝土结构，斜拉索按照扇形双索面布置，斜拉索采用高强度预应力钢绞线，每跨分别布置18对，全桥共有72根斜拉索。主梁结构形式为单箱双室截面，混凝土材料标号为C50，主塔混凝土材料标号为C40。桥型布置见图1。

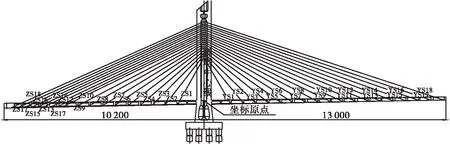
图1 桥型立面布置示意图(单位： cm)

使用有限元软件建立该桥仿真分析模型，主塔采用梁单元模拟，墩底固结，斜拉索与主塔之间共节点，索梁之间使用弹性连接模拟，主梁桥面使用梁格法模拟，约束条件使用简支梁边界，根据设计图纸模拟其施工阶段，有限元模型见图2。

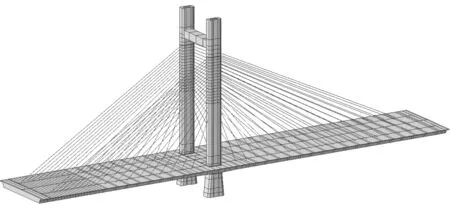
图2 有限元模型示意图

2 基于能量法的索力优化数学模型

混凝土斜拉桥体系中，索力调整的目标是保证主梁在施工及成桥运营状态下不出现开裂，故主梁拉应力应尽可能小，即主梁弯曲应变能应尽可能小，以弯曲应变能表示的优化目标公式可表述为式(1)形式。

(1)

式中：U为主梁弯曲应变能；M(s)为主梁各节段弯矩；Q(s)为主梁各段剪力；EI为主梁弹性模量，在索力优化过程中，忽略弹性模量变化对索力的影响，将弹性模量视为定值。

在式(1)中，仅考虑了弯矩及剪力效应对主梁弯曲应变能的贡献，轴向力偏心造成的弯矩和扭矩效应后继再进行研究。设定目标函数后，设置对应的约束条件及评价函数。对于该桥可将以下条件作为约束条件： ① 混凝土主梁在施工及考虑10a收缩徐变时主梁混凝土拉应力不超限，即σimax≤1.83 MPa；②根据设计文件，该桥斜拉索应保持3倍以上安全系数，即σfmax≤620 MPa；③ 混凝土主塔在各工况下拉应力不超过C40混凝土抗拉强度设计值，即σTmax≤1.71 MPa。

根据以上目标函数及约束条件，以斜拉索索力为设计变量，即可构建完整的数学优化模型。在模型优化过程中，应构造合适的评价函数对优化方向进行限制，以便加快其迭代速度，每次对斜拉索索力的调整必将引起拉索伸长或缩短，当拉索变化量在沿索长方向上变化量为最小时，此时由索力形成的主梁弯曲应变能则最小，因此评价函数可设置为以下形式。

(2)

式中：u表示各斜拉索沿索长方向的位移量。

由于斜拉索优化是一个复杂的迭代过程，若使用正装迭代法则需计算每根索的影响矩阵，而高次超静定体系中，求解影响矩阵极其繁琐且容易出错，而基于遗传理论的优化算法通过建立输入层和输出层的映射关系，可规避正装法中对影响矩阵复杂刚度矩阵的求解。

遗传算法求解索力的主要流程如下：① 以斜拉索索力为自变量，生成初始迭代种群，在Matlab中设置输入及输出层参数；② 以式(1)作为目标函数，同时把约束条件输入至Matlab中，调用神经网络模块进行全局优化，以式(2)作为评价函数，每次迭代优化后对其进行拉索位移量检验，将各斜拉索索力方向的位移量作为一种群，使用评价函数对种群里每个个体进行验证，若满足评价函数要求，则进行下一步迭代，若不满足要求，则重新进行计算，直至满足要求为止; ③ 对于不满足要求的种群，引入精英策略，对初始种群进行优化，提高种群优秀个体百分比，然后再重复以上步骤；④优化完成后，进入后处理提取结果。

3 优化结果

在Matlab中完成优化过程后，将设计变量优化结果输入至有限元模型中，提取该状态下主梁力学响应结果。为节约篇幅，表1仅给出右跨索力优化前后的对比结果。

表1计算结果表明：相比于设计索力，优化后部分节段索力值变化较为明显，如初始索力较小的YS1～YS2、YS17～YS18节段，优化后索力值有明显增大，变化幅度均在10%以上，而对于中间索力值较大的节段，优化后索力值则有了一定程度的下降，如YS9～YS10节段，优化后索力分别下降了6.97%、6.68%。通过对初始索力调整，实现了索力在沿主梁方向的重分布，降低了各斜拉索索力之间的差值幅度，索力分布更为均匀。

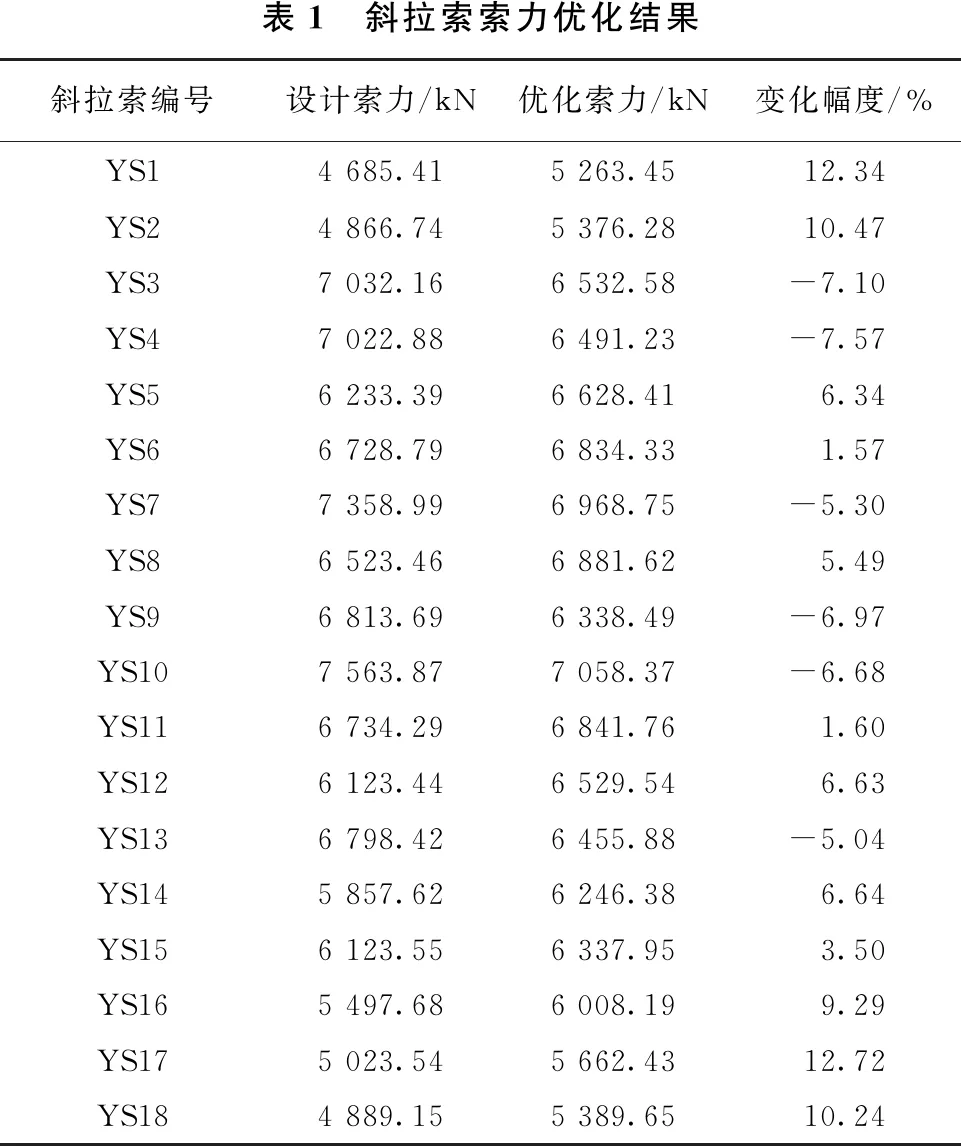
表1 斜拉索索力优化结果斜拉索编号设计索力/kN优化索力/kN变化幅度/%YS14 685.415 263.4512.34YS24 866.745 376.2810.47YS37 032.166 532.58-7.10YS47 022.886 491.23-7.57YS56 233.396 628.416.34YS66 728.796 834.331.57YS77 358.996 968.75-5.30YS86 523.466 881.625.49YS96 813.696 338.49-6.97YS107 563.877 058.37-6.68YS116 734.296 841.761.60YS126 123.446 529.546.63YS136 798.426 455.88-5.04YS145 857.626 246.386.64YS156 123.556 337.953.50YS165 497.686 008.199.29YS175 023.545 662.4312.72YS184 889.155 389.6510.24

为验证索力优化效果，应对目标函数进行检验，在各项指标中，主梁最大拉应力能直接反映节段弯曲应变能的变化，因此，在有限元模型中提取各节段在施工过程中最大拉应力，并将优化前后结果进行对比(见表2)。

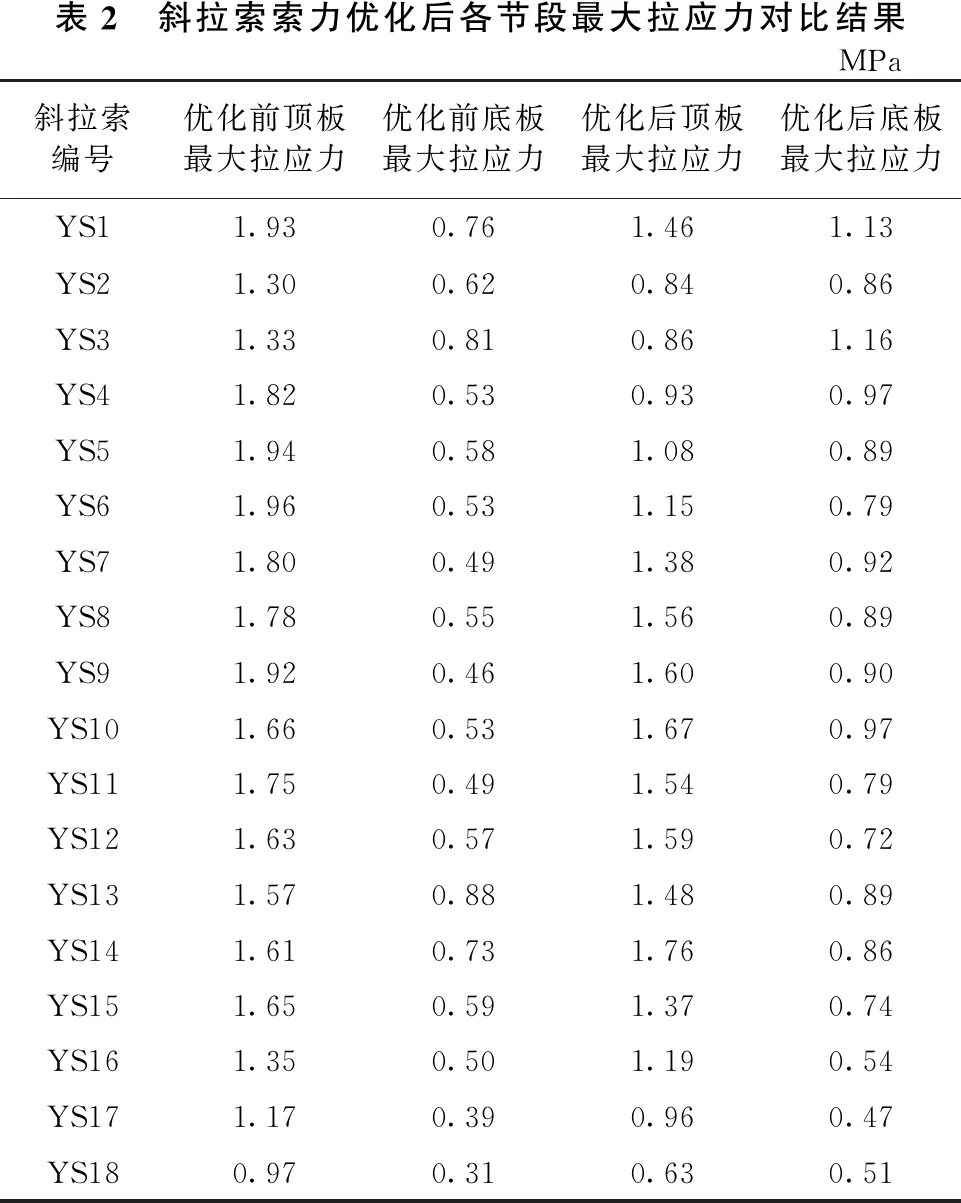
表2 斜拉索索力优化后各节段最大拉应力对比结果 MPa 斜拉索编号优化前顶板最大拉应力优化前底板最大拉应力优化后顶板最大拉应力优化后底板最大拉应力YS11.930.761.461.13YS21.300.620.840.86YS31.330.810.861.16YS41.820.530.930.97YS51.940.581.080.89YS61.960.531.150.79YS71.800.491.380.92YS81.780.551.560.89YS91.920.461.600.90YS101.660.531.670.97YS111.750.491.540.79YS121.630.571.590.72YS131.570.881.480.89YS141.610.731.760.86YS151.650.591.370.74YS161.350.501.190.54YS171.170.390.960.47YS180.970.310.630.51

表2列出了斜拉桥右跨各节段在施工过程中的最大拉应力对比结果，在索力优化前，部分节段混凝土顶板最大拉应力已超过主梁材料限值，而底板拉应力值较小，这是由于设计索力一般未考虑施工期的临时荷载，导致部分节段索力结果偏小，索力调整后优化了主梁受力状态，各节段顶板拉应力均有不同程度下降，并且均在材料强度允许范围内；优化后底板拉应力有一定增大，这是由于部分节段设计索力较小，底板部分材料未充分发挥其性能，通过调整索力，改变了应力在截面上的分布，由表2可知，优化后底板最大拉应力相比材料抗拉强度限值仍有较大富裕度，故认为优化程序取得了良好的效果，通过对索力实施调控，有效控制了混凝土主梁在施工期拉应力。