基于图论方法的SHA-1 差分路径的精准概率计算*
2021-07-22李婧瑜李德刚
李婧瑜, 杨 阳,2, 曾 光, 李德刚
1. 中国人民解放军战略支援部队信息工程大学 数学工程与先进计算国家重点实验室, 郑州 450001
2. 中国科学院 软件研究所 可信计算与信息保障实验室, 北京 100190
1 引言
SHA-1 算法由美国国家安全局[1]设计, 1994 年被美国国家标准与技术研究院(NIST) 发布作为联邦信息处理标准(FIPS), 该算法一经提出就受到各国密码学家的广泛关注. 2005 年, 王小云教授[2]通过模差分攻击技术和消息修改技术把对SHA-1 随机碰撞攻击的复杂度降到了269, 这也是首次将SHA-1 随机碰撞攻击的复杂度降到生日攻击以下. 随后, 很多团队尝试利用该方法对减轮的SHA-1 算法进行碰撞攻击[3–6]. 直到2017 年, Stevens 与Google[7]宣布了一个成功的SHA-1 碰撞攻击, 并且发布了两份内容不同但SHA-1 散列值相同的PDF 文件作为证明. 这是目前为止对SHA-1 的最好的随机碰撞攻击结果.对SHA-1 的另一攻击手段是选择前缀碰撞攻击, 这一类的攻击最好结果由Leurent 和Peyrin[8]在2020年发布, 他们以263.4的复杂度完成了对SHA-1 的选择前缀攻击.
在对SHA-1 的随机碰撞攻击和选择前缀攻击过程中, 构造差分路径和根据差分路径寻找碰撞是两种攻击中共同的步骤. 在构造差分路径方面, 现已由早期的手动构造方法[2]发展为自动化的差分路径构造算法[9–11]. 差分路径的成立概率很大程度上决定了寻找碰撞的成功率和复杂度, 所以对概率的高精度刻画在攻击过程中是十分重要的. 在早期的SHA-1 碰撞攻击研究过程中, 往往以充分条件的个数来决定差分路径成立概率[12,13], 设由差分路径推导的充分条件的个数为k, 则认为该差分路径成立的概率大约为1/2k. 2007 年, Mendel 等人[14]提出了在允许比特扩展且局部碰撞之间相互独立的条件下, 对攻击复杂度的评估方法. 2011 年, Manuel[15]证明了目前公布的扰动向量只有Type-I 和Type-II 两类. 随后,Stevens[11]提出了联合概率的概念, 给出的概率模型是在同时满足所有局部碰撞的条件下得到的, 对差分路径的成立概率刻画的精度更高.
本文对Stevens 提出的基于联合概率的差分路径概率模型进一步分析, 给出其中第三部分的所有结构和相应的概率特征, 最后给出实例以佐证.
2 SHA-1 算法
SHA-1 算法采用MD 迭代结构, 可以将任意长度的输入消息压缩成160 比特的Hash 值. 算法分成消息填充、消息扩展和压缩函数三个部分.
消息填充在输入消息的最后先填充一个1, 再填充若干个0, 使得填充后的消息长度l满足l ≡448 mod 512, 再将原始消息的长度转换成64 比特二进制的形式填充到消息末尾, 此时消息长度是512 的整数倍, 这就是消息填充过程.
消息扩展设填充后的消息长度为512K比特, 每个512 比特为一个消息块, 分别记为M0,M1,···,MK−1. 消息扩展过程是将每个512 比特的消息块扩展成80 个32 比特的消息字. 每个消息块由16 个32 比特的消息字组成, 将第k+1 个消息块Mk记为W0,k,W1,k,··· ,W15,k, 则对Mk的消息扩展准则如下式, 其中RL(W,b) 代表将32 比特向量W循环左移b比特:
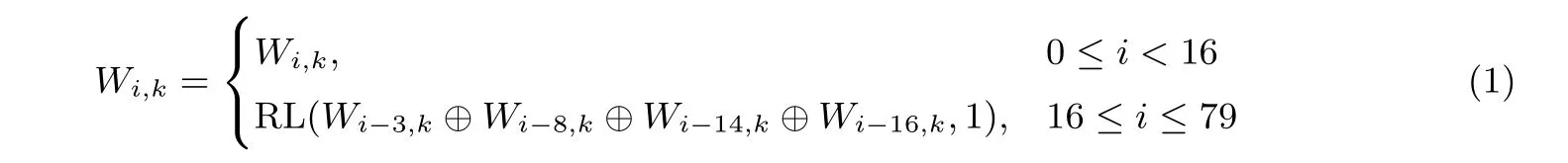
接下来扩展后的消息块依次进入压缩函数, 当处理第k+1 个消息块Mk时, 压缩函数以Mk和上一个消息块的压缩函数输出IHVk=(ak,bk,ck,dk,ek) 作为输入(ak,bk,ck,dk,ek为32 比特消息字), 输出结果为160 比特的消息摘要IHVk+1, 即IHVk+1= Compress(IHVk,Mk), 处理第一个消息块M0的初始值取值为IHV0=(a0,b0,c0,d0,e0):

这样, 最后一个消息块MK−1进入压缩函数后的输出结果IHVK即为最终的SHA-1 哈希值.
压缩函数第k+1 个消息块Mk经过消息扩展后进入压缩函数的过程如下: 由上一步的压缩结果IHVk= (ak,bk,ck,dk,ek), 令5 个寄存器的初始值为(Q0,Q−1,Q−2,Q−3,Q−4) = (ak,bk,RR(ck,30),RR(dk,30),RR(ek,30)), 其中RR(W,b) 代表将32 比特向量W循环右移b比特.
然后进行4 轮(每轮20 步) 迭代计算, 每次迭代均输入一个扩展后的消息字, 第t(0≤t ≤79) 步的迭代方程为:Qt+1=RL(Qt,5)+Ft+RL(Qt−4,30)+Wt,k+ACt. 其中:
(1)Ft=ft(Qt−1,RL(Qt−2,30),RL(Qt−3,30)),ft是以三个比特为输入的布尔函数, 其在每一轮的表达式分别为:
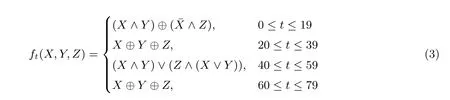
(2) ACt是轮常数, 其在每一轮的取值如下:
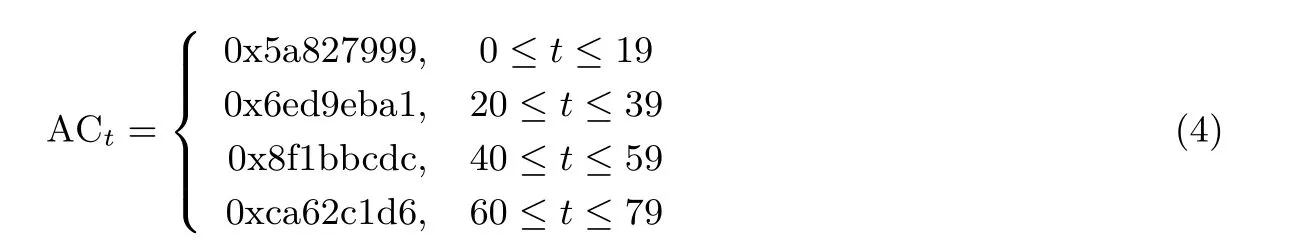
80 步迭代之后, 压缩函数的输出为IHVk+1= (ak+1,bk+1,ck+1,dk+1,ek+1) = (ak+Q80,bk+Q79,ck+RL(Q78,30),dk+RL(Q77,30),ek+RL(Q76,30)).
3 基于联合概率的差分路径概率模型
为了完整性, 本节介绍文献[11] 所提出的一种新的基于联合概率的差分路径概率模型. 该模型通过提出概率实验1, 从理论上对差分路径的概率进行了精准刻画. 进一步, 为了方便对实验的成功率进行刻画, 将实验1 改进得到概率实验2. 然而, 在概率实验1 和2 中, 都存在取值空间过大、无法穷举的问题.为了解决这一问题, 文献[11] 结合图论方面的知识, 通过对差分路径上的寄存器差分和布尔函数差分的拆

概率实验1
对于第一块消息, 随机选择初始寄存器值 ˆQtb−4,··· ,ˆQtb和第tb到te步的扩展消息字ˆWtb,··· ,ˆWte, 然后计算第一块消息在第tb到te步的布尔函数值并更新寄存器值, 其中t=tb,··· ,te:
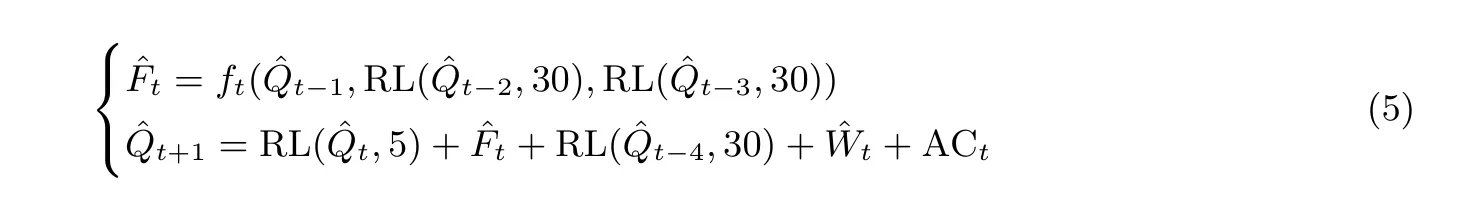
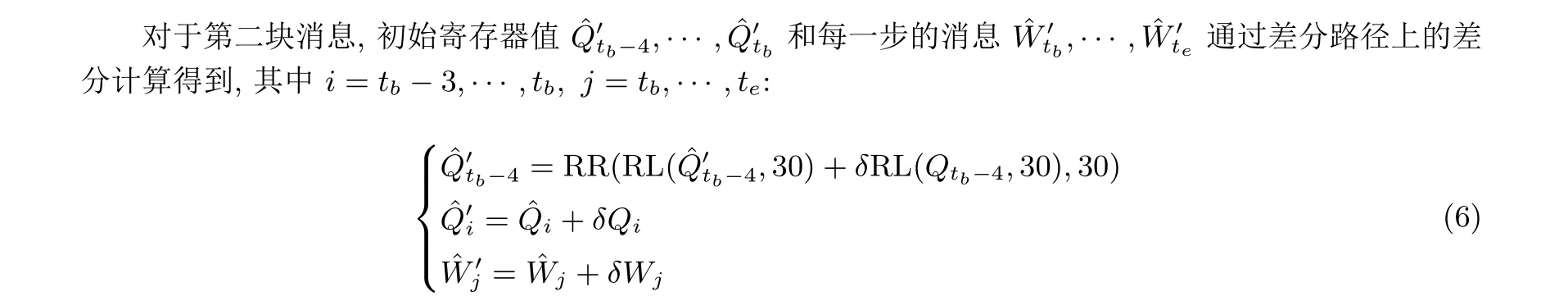
然后根据SHA-1 算法的压缩函数计算每一步的布尔函数值, 并更新寄存器值, 其中t=tb,··· ,te:
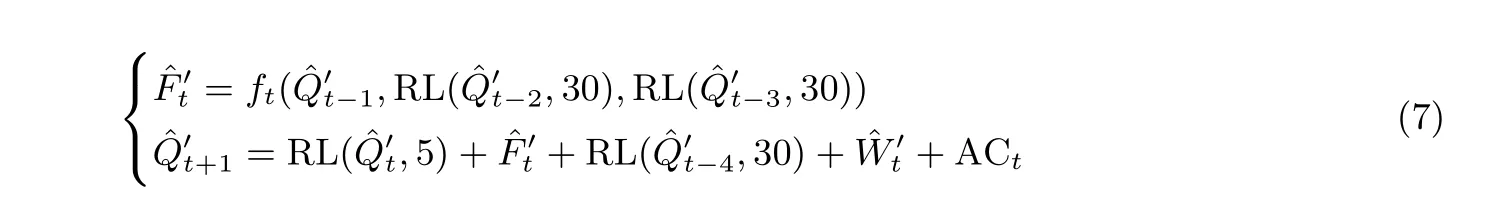
得到两块消息相关变量的取值后, 判断两个消息块的寄存器差分和布尔函数差分是否与差分路径吻合, 即判断:

对于第二块消息, 各个变量的计算方法与实验1 一致. 判断实验是否成功的条件也与实验1 一致.
可以看到, 实验1 在第一块消息上首先随机选择消息字, 再计算寄存器值. 而实验2 与这一过程相反,即先随机选择寄存器值, 再计算消息的值. 经过实验1 到实验2 的转变, 随机选择的变量完成了由两类向一类的整合(实验1 需要随机选择寄存器值和消息值两类变量, 而实验2 中需要随机选择的变量只有寄存器值一类).

第一部分
设差分路径上非零的寄存器差分对应的比特位集合为GΔQ={(j,i)|∆Qj[i]̸= 0, j ∈ {tb −3,··· ,te}, i ∈{0,··· ,31}}. 对于集合GΔQ中元素(j,i), 为了取得实验2 的成功, 若∆Qj[i] = +1,则随机选择的第一块消息的 ˆQj必须满足 ˆQj[i] = 0; 若∆Qj[i] =−1, 则随机选择的第一块消息的 ˆQj必须满足 ˆQj[i] = 1, 这两种情况的成立概率均为1/2. 所以GΔQ中的比特位满足差分路径的概率为pΔQ=2−|GΔQ|.
第二部分
给定差分路径上第t步的布尔函数的三个输入寄存器差分为∆Qt−1,∆Qt−2,∆Qt−3, 对于满足这三个寄存器差分的3 对寄存器取值, 将第b比特上所有可能的布尔函数输出差分组成的集合记为Vt,b:

设SF={(t,b)||Vt,b|> 1}, 考虑满足以下两个条件的寄存器比特位(j,i): 1○对应的寄存器差分为零, 即∆Qj[i]=0; 2○(j+1,i),(j+2,i −2),(j+3,i −2) 中至少有一个在集合SF中. 即

第三部分

命题2在上述分割方法下, 差分路径的概率分解成若干个因子的乘积:

4 基于图论方法的精确概率特征计算
本小节对第3 节中的第三部分概率做进一步的理论分析. 按照第3 节的分割方法, 第三部分主要考虑布尔函数输出差分不唯一时的成立概率. 对于SHA-1 算法在后三轮所采用的布尔函数—异或函数和择多函数, 分析总结其输出差分规律. 进一步, 结合图论相关知识分析第三部分中连通分支的结构特征和概率特征. 首先提出本文所涉及的图论的基本概念.
定义1一个集合的元素和它们之间的某种关系称为图. 具体地说, 图是一个二元组(V,E), 其中集合V称为节点集, 集合V中由两个元素组成的无序对的集合E称为边集. 图的节点集中的元素称为节点,边集中的元素称为边. 节点的数目|V| 称为图的阶, 边的数目|E| 称为图的边数.
例 1给定G= (V,E), 其中节点集V={v1,v2,v3,v4,v5}, 边集E={(v1,v2),(v3,v4),(v1,v5),(v5,v5)}. 这便定义出一个图. 节点v1和v2称为边(v1,v2) 的端点, 反过来也称边(v1,v2)连接节点v1和v2.
定义2(点和点的相邻) 如果图上两点被同一条边相连, 则称该两点在图中相邻.
定义3(点和边的关联) 如果在图G中节点v是边e的一个端点, 则称节点v与边e在图G中相关联.
定义4(节点的度) 图G中节点v所关联的边的数目称为节点v的度, 记为dG(v) 或d(v).
定义5图G中一个点边接续交替出现的序列w=vi0ei1vi1ei2···eikvik称为图G的一条途径, 其中vi0,vik分别称为途径w的起点和终点,w上其余节点称为中途点. 图G中边不重复出现的途径称为迹. 图G中顶点不重复出现的迹称为路.
定义6设G是一个图,V′⊆V(G). 以V′为节点集, 以G中两端点均属于V′的所有边作为边集所组成的子图, 称为G的由节点集V′导出的子图, 简称为G的点导出子图, 记为G|V′|.
定义7(图中两点的连通) 如果在图G中u,v两点间有路相通, 则称节点u,v在图G中连通. 若图G中任两节点都相通, 则称图G是连通图.
定义8(图的连通分支) 若图G的节点集V(G) 可划分为若干非空子集V1,V2,···Vw, 使得两节点属于同一子集当且仅当它们在G中连通, 则每个点导出子图G|Vi| 为图G的一个连通分支(i=1,2,··· ,w).G的连通分支的个数称为G的连通分支数.
在本文所涉及的图中, 节点分为两类, 一类代表寄存器比特位, 另一类代表布尔函数比特位. 另外, 图中相邻的两个点属于不同类节点, 即边的端点均为一个寄存器比特位和一个布尔函数比特位.
定理1对于异或函数f(X,Y,Z)=X ⊕Y ⊕Z, 给定X,Y,Z上的差分∆X,∆Y,∆Z, 定义集合
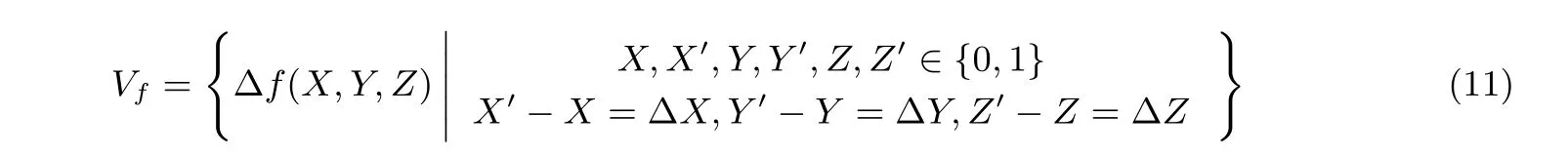
则|Vf|> 1⇔∆X,∆Y,∆Z中有且仅有一个为非零, 即存在六种输入寄存器差分的取值使得布尔函数的输出差分不唯一, 这六种取值分别为三个输入中的其中一个为正差分或负差分.
证明:1)|Vf|>1⇒∆X,∆Y,∆Z中有且仅有一个为非零.
在布尔函数f(X,Y,Z) =X ⊕Y ⊕Z的三个输入比特上, 每个比特上的差分都有三种取值: 0、+1和−1, 所以三个输入比特差分共有27 种取值情况. 将∆X,∆Y,∆Z的27 种取值遍历, 计算每种取值下的集合Vf, 将所有|Vf|> 1 的情况汇总得到表1(左), 可以从中发现寄存器差分的规律: 输入寄存器差分∆X,∆Y,∆Z中有且仅有一个为非零.
2) ∆X,∆Y,∆Z中有且仅有一个为非零⇒|Vf|>1.
当∆X,∆Y,∆Z中有且仅有一个为非零时, 由表1(左),|Vf|>1.
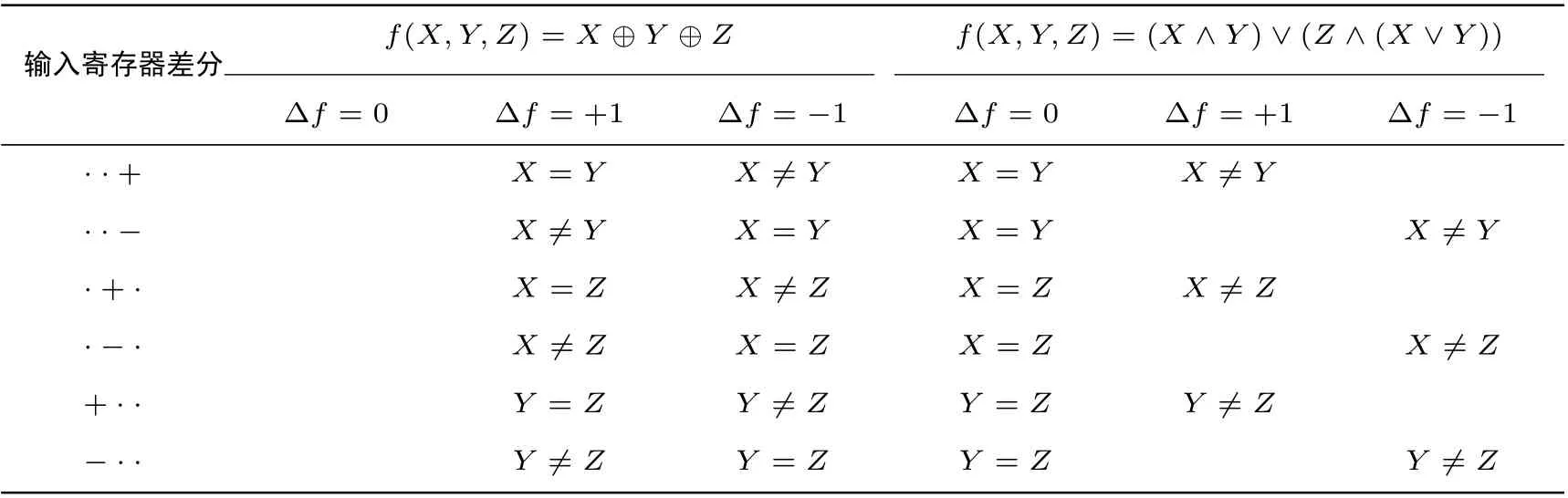
表1 布尔函数输出差分不唯一的所有情况Table 1 All cases where Boolean function output difference is not unique
表注: 每个Vf中的元素下的等式或不等式是为了得到相应的输出差分而对两个不存在差分的寄存器的取值提出的制约条件. 以第一行为例, 当三个输入寄存器比特上的差分为··+ 时(即∆X=0、∆Y=0和∆Z=+1),集合Vf中存在两个元素: +1 和−1. 其中,∆f(X,Y,Z)=+1 时要求X′=X=Y=Y′,而∆f(X,Y,Z)=−1 时要求X′=X,Y=Y′,X ̸=Y.
定理2将定理1 中的异或函数替换成择多函数f(X,Y,Z)= (X ∧Y)∨(Z ∧(X ∨Y)), 结论依然成立.
证明:将异或函数替换成择多函数f(X,Y,Z) = (X ∧Y)∨(Z ∧(X ∨Y)), 同样计算27 种输入差分取值下的集合Vf, 将|Vf|>1 的情况汇总得到表1(右). 其余证明过程与定理1 同理.
根据定理1 和定理2 可以得到以下定理和推论:
定理3连通分支FQk中每个布尔函数比特位的度均为2.
证明:在连通分支FQk(k=1,2,··· ,K) 中, 对于(t,b)∈SF, 由定理1 和定理2 可知,Ft[b] 的三个输入寄存器差分∆Qt−1[b], RL(∆Qt−2,30)[b], RL(∆Qt−3,30)[b] 中有且仅有一个为非零, 其中20≤t<79,b=0,1,··· ,31. 即在连通分支FQk(k=1,2,··· ,K) 中, 每个布尔函数比特位(t,b)∈SF一定与两个输入寄存器比特位相连接, 故而该点在连通分支中的度为2.

定义9将含有l个布尔函数比特位、l+1 个寄存器比特位的连通分支称为l-l+1 型连通分支.
综合以上分析, 所有连通分支的类型为1-2 型、2-3 型、3-4 型等. 显然, 1-2 型和2-3 型连通分支只有一种结构, 而3-4 型连通分支由于一个寄存器比特位的度的不确定性可以分为两种结构, 图1 列举了1-2型、2-3 型、3-4 型连通分支的所有结构. 在每个类型的连通分支中, 上层节点均为布尔函数比特位, 自左向右分别记为F1,F2,··· ,下层节点均为寄存器比特位, 自左向右分别记为Q1,Q2,··· .
定理4在由Type-I 和Type-II 类扰动向量得到的差分路径中, 图1 中3-4 型(2) 的结构不存在.
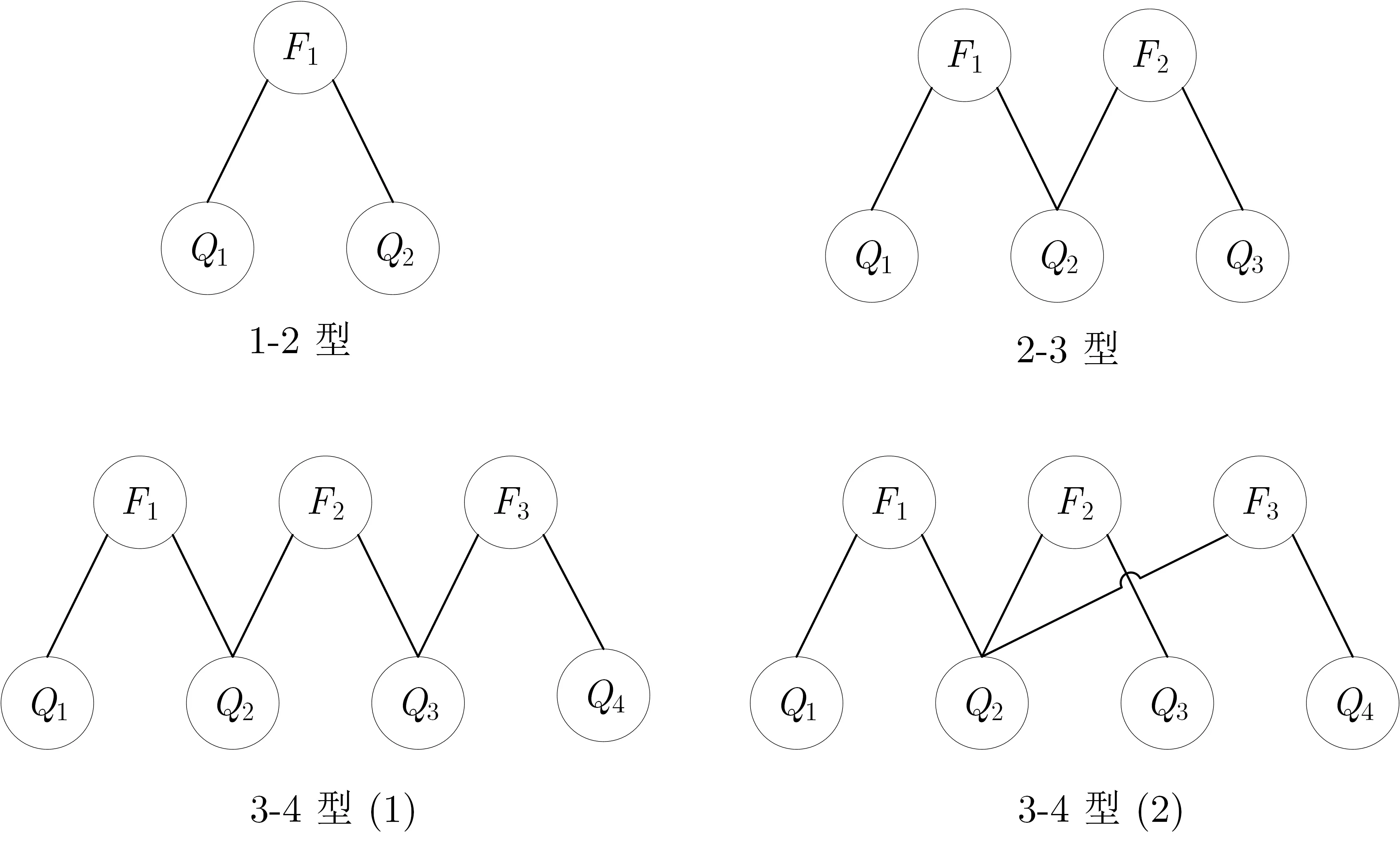
图1 连通分支的结构Figure 1 Structure of connected branches
证明:首先分析一个寄存器比特位在连通分支中的结构特点. 对于寄存器比特Qj[i], 其中i=0,1,··· ,31 且20≤j<79, 存在三个布尔函数比特位以其作为输入, 分别为
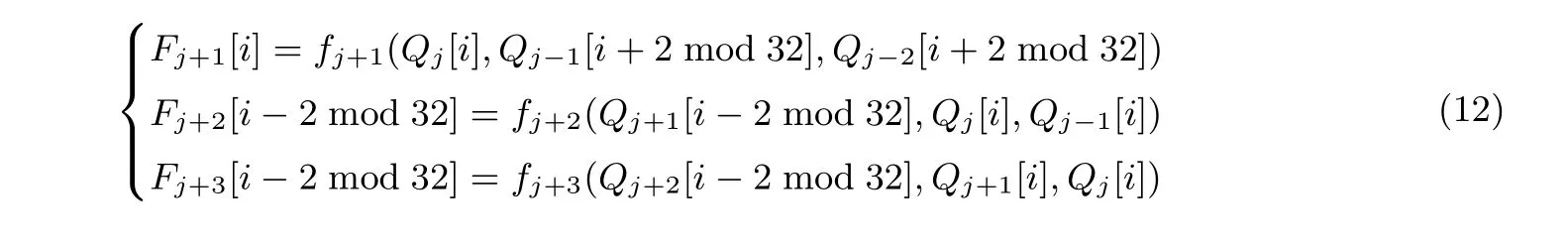
由集合SQ的含义以及定理3, 当∆Qj[i] = 0 且三对寄存器比特Qj−1[i+2 mod 32] 和Qj−2[i+2 mod 32]、Qj+1[i −2 mod 32] 和Qj−1[i]、Qj+2[i −2 mod 32] 和Qj+1[i] 中至少有一对比特上的差分为零和非零的组合时, 有(j,i)∈SQ.
下面证明连通分支中一个寄存器比特位的度不可能为3.
假设(j,i)∈SQ且在连通分支中的度为3, 则(j,i)∈SQ与三个布尔函数位(分别为(j+1,i),(j+2,i −2),(j+3,i −2)∈SF) 相连接, 则三对寄存器比特Qj−1[i+2 mod 32] 和Qj−2[i+2 mod 32]、Qj+1[i −2 mod 32] 和Qj−1[i]、Qj+2[i −2 mod 32] 和Qj+1[i] 上的差分均为零和非零的组合, 具体有8种情况见表2.
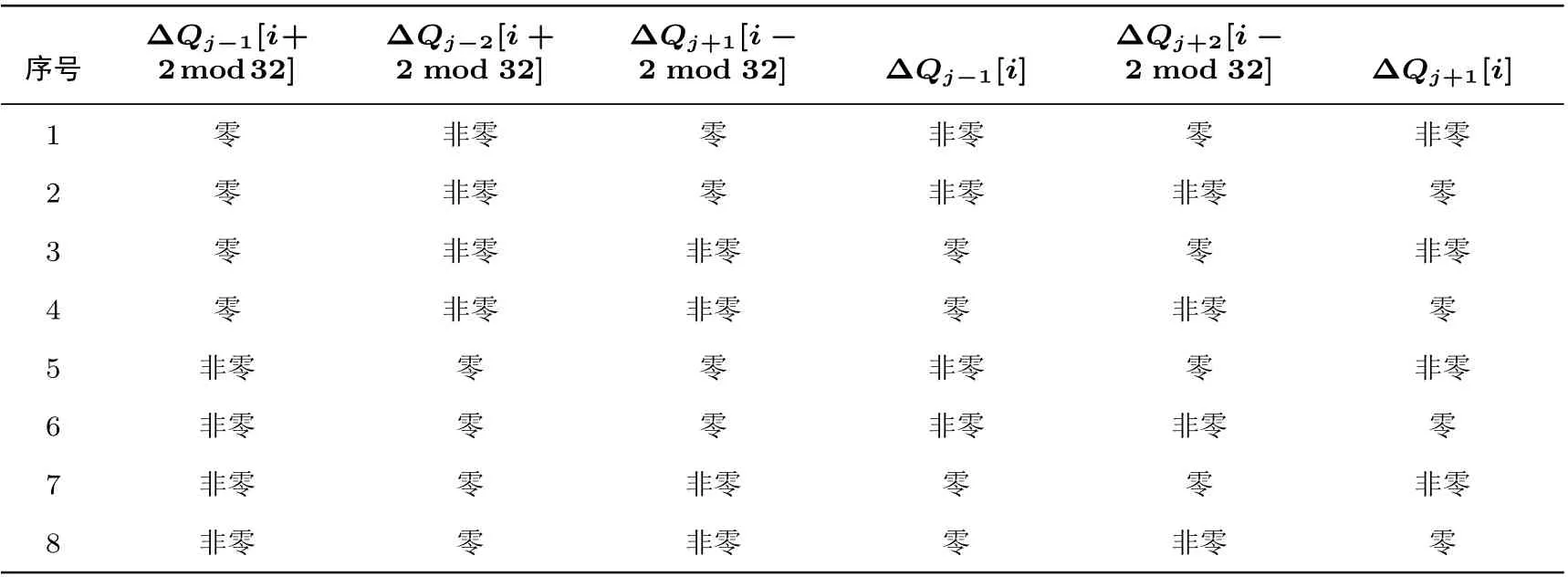
表2 d((j,i))=3 时要求寄存器差分的取值情况Table 2 Value of register differential required for d((j,i))=3
针对表2 中的第一种情况进行分析: 首先, 在后60 步差分路径上, 寄存器上的差分(不考虑差分的正负) 与扰动向量是一致的, 即∆Qj[i]̸= 0 当且仅当扰动向量满足DVj−1[i] = 1, 反之, ∆Qj[i] = 0 当且仅当扰动向量满足DVj−1[i] = 0. 所以, 表2 的第一种情况要求扰动向量满足: 对于i= 0,1,··· ,31 和20≤j< 79, DVj−1[i],DVj−2[i+2 mod 32],DVj[i −2 mod 32],DVj+1[i −2 mod 32] 的取值为0, 而DVj−3[i+2 mod 32],DVj−2[i],DVj[i] 的取值为1. 文献[15] 中证明了最优扰动向量存在两类(Type-I和Type-II), 目前为止对SHA-1 的碰撞攻击中用到的扰动向量有
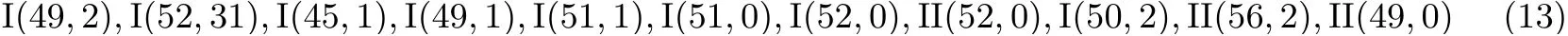
附录列出了这些扰动向量的后60 步在通式I(K,0) 和II(K,0) 中涉及的最大范围. 将上述条件和附录对比发现Type-I 和Type-II 类扰动向量不能满足表2 中第一种情况. 对表2 中另外7 种情况进行同理分析, 最终结论为: 对于Type-I 和Type-II 类扰动向量, 表2 中的8 种情况均不可能存在, 故连通分支中寄存器比特位的度小于3, 即图1 中3-4 型(2) 的结构不存在.
定理5在由Type-I 和Type-II 类扰动向量得到的差分路径中, 图1 中3-4 型(1) 的结构不存在.
证明:对于图1 中3-4 型(1) 的结构, 固定Q2点为(j,i), 在此基础上分析其他寄存器比特位和布尔函数位的取值情况. 与Q2点相连的两个布尔函数位F1和F2从(j+1,i),(j+2,i −2),(j+3,i −2) 中选择, 由于F1和F2两点在3-4 型(1) 结构中的地位是不对等的, 所以共有6 种选择. 然后, 在F2的除Q2外的两个输入寄存器比特中选择一个确定为Q3点(2 种选择), 再在以Q3点为输入的除F2外的两个布尔函数位中选择一个确定为F3(2 种选择). 最后确定Q1和Q4(均有2 种选择). 所以, 在固定节点Q2点后, 3-4 型(1) 结构的连通分支上所有点的取值共有6×2×2×2×2=96 种情况.
与定理4 的证明过程同理, 将96 种情况对照附录进行分析, 发现Type-I 和Type-II 类扰动向量不能满足上述条件. 另外发现有些情况本身就存在矛盾. 总之, 96 种情况均不可能存在, 所以3-4 型(1) 结构的连通分支在由Type-I 和Type-II 类扰动向量得到的差分路径中不可能存在.
推论2在由Type-I 和Type-II 类扰动向量得到的差分路径中, 本文的概率模型的第三部分中连通分支的结构只可能有1-2 和2-3 型两种.
证明:假设存在l-l+1 型连通分支(l> 3), 则一定内嵌有3-4 型(1) 和3-4 型(2) 结构. 结合定理4 和定理5, 在由Type-I 和Type-II 类扰动向量得到的差分路径中, 只可能有1-2 和2-3 型两种结构的连通分支.
定理6l-l+1 型连通分支SQ中寄存器比特位的取值满足差分路径的概率为2/2l+1.
证明:设一个l-l+1 型连通分支SQ中的寄存器比特位分别为(j1,i1),··· ,(jl,il),(jl+1,il+1), 对应Qj1[i1],··· ,Qjl[il],Qjl+1[il+1]. 其中一个位置Qjm[im],m=1,2,··· ,l在取定0 或1 其中一个值后,由表1 可以确定这些比特位的取值以得到差分路径指定的布尔函数输出差分, 即与Qjm[im] 的关系都确定为“相等” 或“不相等”. 也就是说, 当确定Qj1[i1],··· ,Qjl[il],Qjl+1[il+1] 中的其中一个取值后, 其余比特位的取值也随之确定. 所以Qj1[i1],··· ,Qjl[il],Qjl+1[il+1] 一共在两种取值下可以满足差分路径. 而l+1 个比特位的取值空间中存在2l+1个元素, 所以这些比特位满足差分路径的概率为2/2l+1.
5 实例及评估
本节以三段具体的差分路径为例, 对其分别按照实验的方法、计数充分条件的方法和本文第3、4 节的方法进行概率计算, 综合三个结果对本文的概率模型进行评估.
实例1
2005 年,王小云[2]针对SHA-1 算法提出了模差分攻击的方法,以269的复杂度给出了对全轮SHA-1算法的碰撞攻击. 随后文献[16] 对其用到的差分路径进行了全轮分析, 本文以文献[16] 整理的差分路径进行概率分析. 以文献[16] 中Figure 3 的第46–56 步的差分路径(记为P46–56) 为例进行概率分析, 差分路径及对应的充分条件如表3, 表中的数字代表存在扰动(第2 列) 或差分不为零(第3–7 列) 的比特位,“-” 代表32 位无扰动或全零差分.
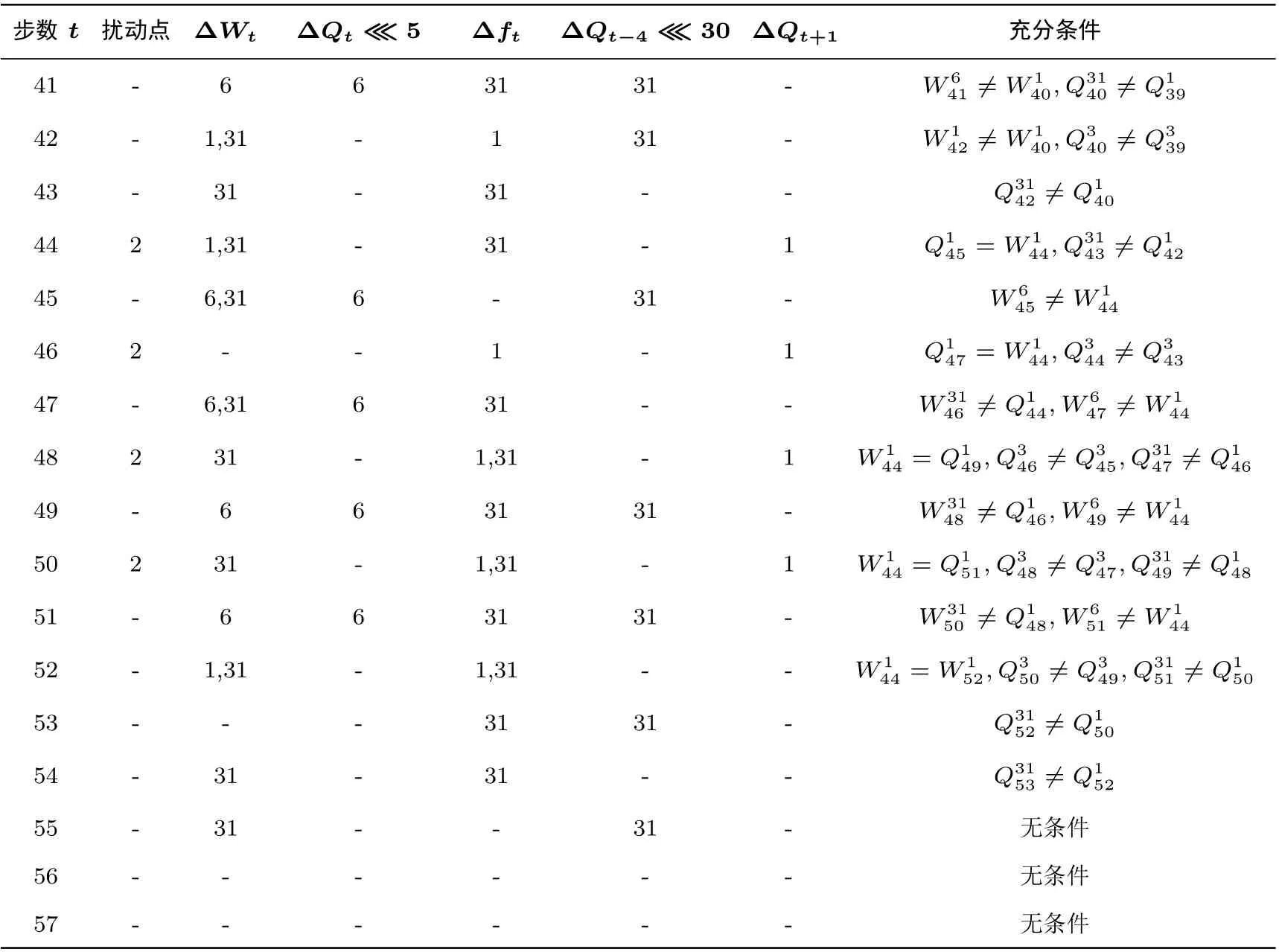
表3 第46–56 步上的差分路径Table 3 Differential path over Steps 46–56
命题3当按照充分条件的个数计算差分路径的概率时, Pr[P46–56]=1/219.
证明:由于在第46–56 步上的充分条件的个数为19, 根据每个充分条件成立的概率为1/2 的原则,所以差分路径P46–56的概率为1/219.
命题4当按照本文的差分路径概率模型计算概率时, Pr[P46–56]=1/216.
证明:当按照第3 节和第4 节中的差分路径概率模型, 差分路径上寄存器差分的情况为:
(1)δRL(Q42,30)=0;
(2) ∆Q43,∆Q44,∆Q46,∆Q48,∆Q50上无差分, ∆Q45,∆Q47,∆Q49,∆Q51均在第1 位上存在正差分;
(3)δQ57=0.
进而可以确定集合GΔQ为GΔQ={(45,1),(47,1),(49,1),(51,1)}, 共四个元素, 所以这一部分对应的概率为1/24.
然后确定集合SF的所有元素. 对于(t,b)∈SF, ∆Qt−1[b],RL(∆Qt−2,30)[b],RL(∆Qt−3,30)[b] 中至少有一个输入差分为非零. 故将每个非零寄存器差分作为布尔函数的输入, 他们影响的所有布尔函数差分如表4, 其中“无” 代表布尔函数输出的32 个比特上差分均为0.
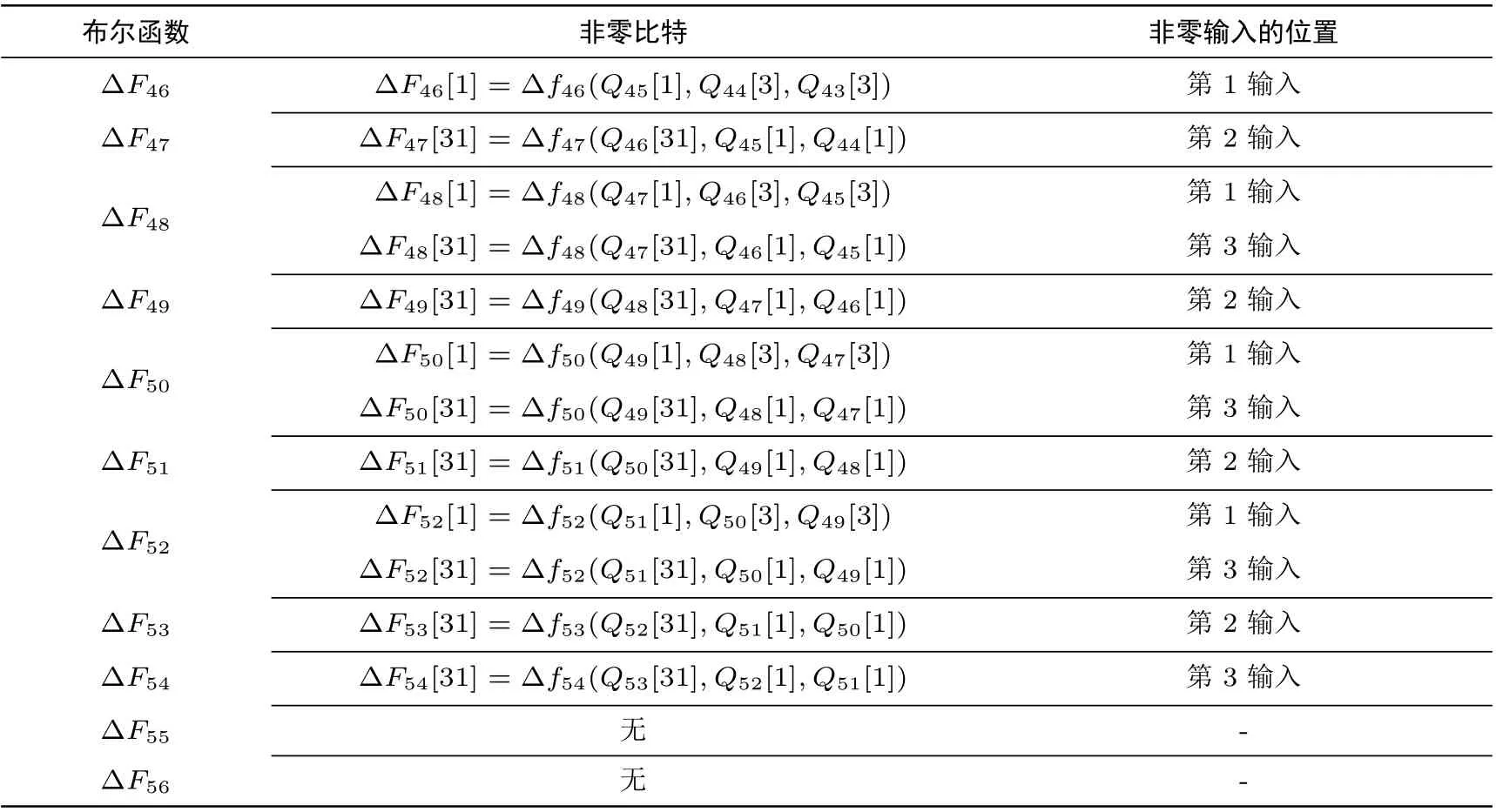
表4 差分路径P46–56 上非零布尔函数差分与非零输入的关系Table 4 Nonzero Boolean function differences and nonzero inputs on differential path P46–56
这 12 个布尔函数比特位均满足有且只有一个输入差分非零, 根据定理1 确定集合SF={(46,1),(47,31),(48,1),(48,31),(49,31),(50,1),(50,31),(51,31),(52,1),(52,31),(53,31),(54,31)}. 进而集合SQ={(44,3),(43,3),(46,31),(44,1),(46,3),(45,3),(47,31),(46,1),(48,31),(48,3),(47,3),(49,31),(48,1),(50,31),(50,3),(49,3),(51,31),(50,1),(52,31),(52,1),(53,31)}.SF和SQ形成集合FQ, 对于(j,i)∈SQ和(t,b)∈SF, 若Qj[i] 是Ft[b] 的一个输入, 则在FQ 中将(j,i) 和(t,b) 连接起来.所连成的图如图2 所示(图2与图1的节点排列方式相同, 连通分支的布尔函数节点位于上层, 寄存器节点位于下层).
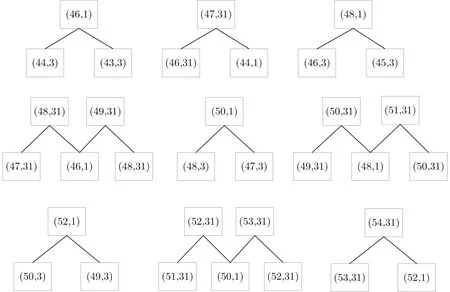
图2 第46–56 步差分路径的所有连通分支Figure 2 All connected branches of differential path over Steps 46–56
可以看到, FQ 中的元素一共形成9 个连通分支, 其中有6 个1-2 型连通分支和3 个2-3 型连通分支.依据定理4, 1-2 型连通分支的概率为2/22, 2-3 型连通分支的概率为2/23. 综上, 这段第46–56 步的差分路径成立概率为2−4×(2/23)3×(2/22)6=1/216.
实例2
本文还对文献[16] 中Figure 3 中的第66–79 步的差分路径进行了相同过程的概率分析, 按照充分条件的个数计算得到的差分路径的概率为1/230, 而按照第3 节和第4 节中的差分路径概率模型计算得到的概率为1/221, 其中第三部分的连通分支结构都是1-2 型的, 具体计算过程不再赘述.
实例3


命题5当按照充分条件的个数计算差分路径的概率时, Pr[P8–16]=1/233.
证明:由于在第8–16 步上的充分条件的个数为33, 根据每个充分条件成立的概率为1/2 的原则, 所以差分路径P8–16的概率为1/233.
命题6当按照充分条件的个数计算差分路径的概率时, Pr[P8–16]=1/228.
证明:当按照第3 节和第4 节中的差分路径概率模型, 差分路径上寄存器差分的情况为:
(1)δRL(Q4,30)=24+25+26+27+28−29−228+231;
(2) ∆Q5–∆Q16上的差分如表5;

表5 第8–16 步上的差分路径P8–16Table 5 Differential path over Steps 8–16
(3)δQ17=231.
进而可以确定集合GΔQ为∆Q5–∆Q16上所有差分为非零的比特位, 根据表5 可知GΔQ中共有18个元素, 所以这一部分对应的概率为1/218.
然后确定集合SF的所有元素. 对于(t,b)∈SF, ∆Qt−1[b], RL(∆Qt−2,30)[b], RL(∆Qt−3,30)[b] 中至少有一个输入差分为非零. 将由表5 中布尔函数上的非零差分总结在表6 中, 分析非零寄存器差分的输入情况.
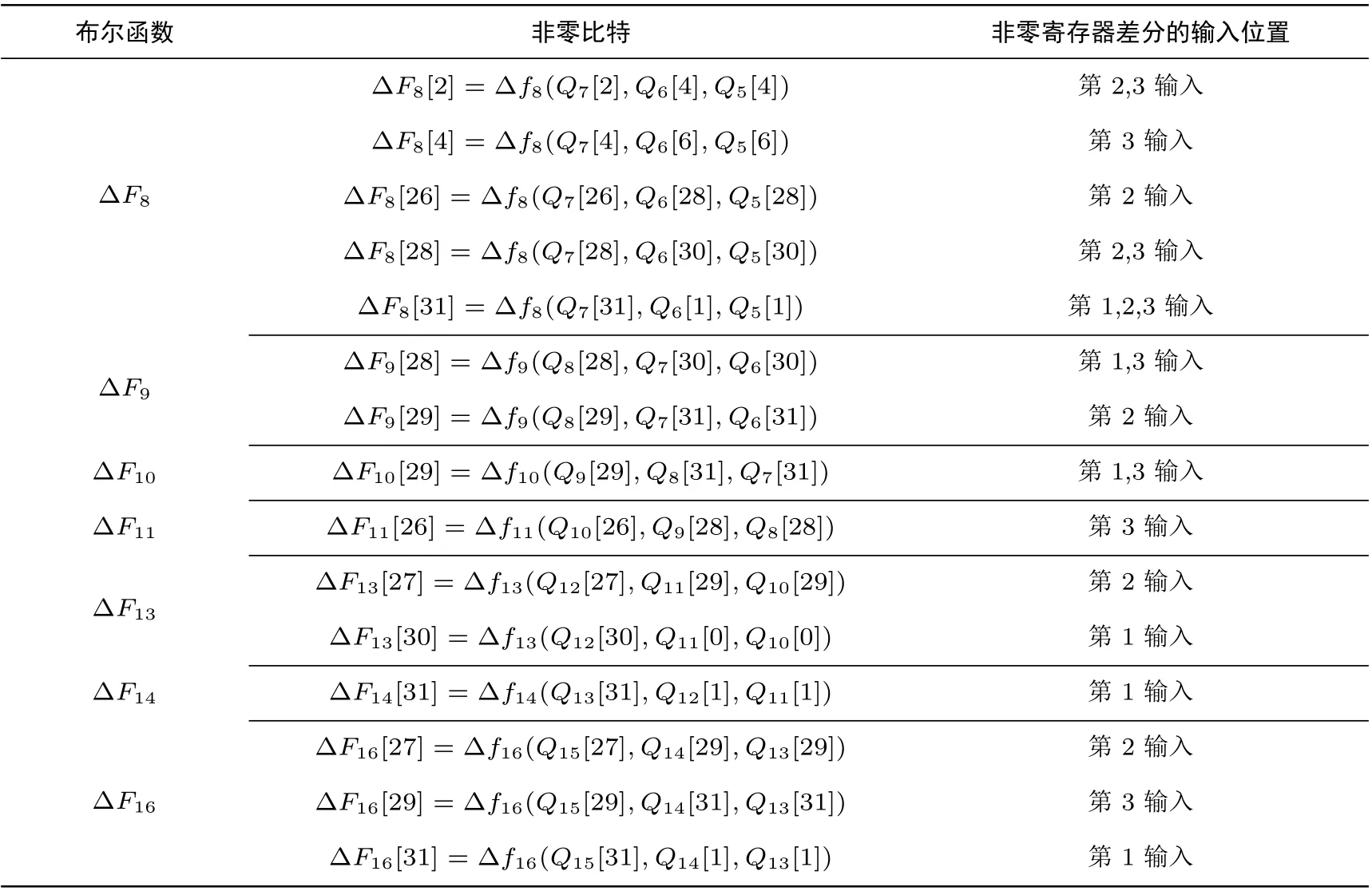
表6 差分路径P8–16 上非零布尔函数差分与非零输入的关系Table 6 Nonzero Boolean function differences and nonzero inputs on differential path P8–16
由定理1 可知, 当存在两个及以上的输入存在非零差分时, 布尔函数的输出值唯一. 所以可以确定集合SF为:
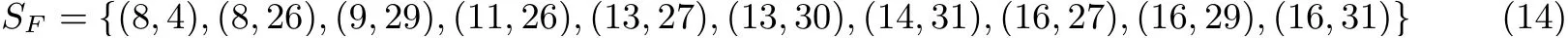
进而集合SQ为:
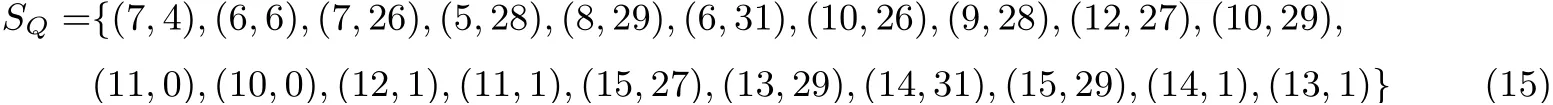
SF和SQ形成集合FQ, 对于(j,i)∈SQ和(t,b)∈SF, 若Qj[i] 是Ft[b] 的一个输入, 则在FQ 中将(j,i) 和(t,b) 连接起来. 所连成的图如图3 所示(图结构和节点的含义同图2):

图3 第6–18 步差分路径的所有连通分支Figure 3 All connected branches of differential path over Steps 6–18
可以看到, FQ 中的元素一共形成10 个1-2 型连通分支. 依据定理6, 每个1-2 型连通分支的概率为2/22, 所以第8–16 步的差分路径成立概率为2−18×(2/22)10=1/228.
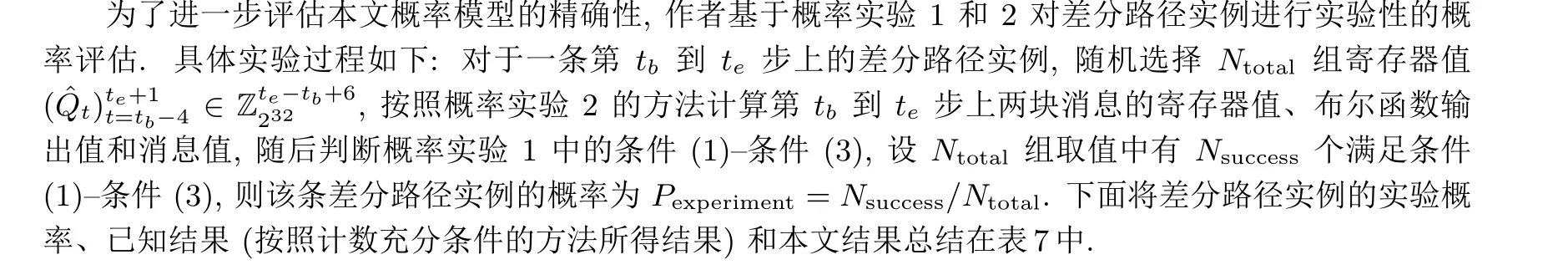
本节的差分路径实例从涵盖的轮数上看, 既包含了第一轮的非线性路径, 也包含了后三轮的线性差分路径部分, 实验结果可见本文的概率模型在刻画差分路径成立概率上的优越性. 从表7 的结果中可以发现,相较本文的概率模型, 按照充分条件的个数计算得到的差分路径概率偏小. 这是因为本文的概率模型是针对差分路径的整体进行概率分析的, 而充分条件个数的方法将差分路径中的局部碰撞视为相互独立的. 由于各个局部碰撞成立的充分条件可能会同一寄存器比特或消息比特做出约束, 充分条件之间存在内在的联系, 所以按照每个充分条件的成立概率均为1/2、同时所有充分条件独立的计算方法会使计算结果偏小.

表7 差分路径实例的不同概率分析结果对比Table 7 Comparison of different probability analysis results of differential paths instance
6 总结
在对SHA-1 的碰撞攻击过程中, 差分路径的构造是非常重要的步骤, 将会直接影响后续寻找碰撞消息对的复杂度. 差分路径的成立概率是考察其优劣的一个重要衡量指标, 所以更精确地刻画差分路径成立的概率有助于对差分路径进行准确评估, 进而对整个碰撞攻击的复杂度进行精准评估. 随机碰撞分为差分路径构造和消息搜索两个阶段, 利用本文的概率模型对文献[16] 中后三轮的差分路径进行分析, 得到其成立概率为1/292, 而该段差分路径成立的充分条件个数为113 个, 这说明本文方法更贴近实际概率. 需要说明的是基于该路径, 消息搜索阶段可利用消息递归技术和高级消息修改技术进一步降低复杂度, 致使差分路径概率与真实的碰撞攻击复杂度存在差距. 本文对Stevens 提出的基于联合概率的差分路径概率模型进行分析, 得出了其中第三部分连通分支的结构特征和概率特征. 从理论上证明了对于两类最优扰动向量, 不存在包含3 个及以上布尔函数比特的连通分支, 明确了每一类连通分支对应的成立概率. 完善之后的概率模型使得差分路径的概率计算过程更为简单, 且较之前的计算方法误差更小.
