ZUC-256 算法的快速软件实现
2021-07-22贾文义朱桂桢
白 亮, 贾文义, 朱桂桢
兴唐通信科技有限公司, 北京 100191
1 引言
祖冲之序列密码算法(即ZUC 算法, 为了和ZUC-256 算法区分, 下文中我们将其称为ZUC-128算法) 使用128 比特密钥, 能够提供数据的机密性和完整性保护功能. 2011 年9 月在日本福冈召开的第三代合作伙伴计划(3GPP)[1]系统架构组(SA) 会议上, ZUC-128 算法被批准写入3GPP 长期演进(LTE) 系统标准规范[2], 用于LTE 空口数据传输保护, 是我国首个成为国际标准的密码算法. 3GPP 基于ZUC-128 算法, 结合LTE 系统实际工作输入输出需要, 制定了机密性保护算法(128-EEA3) 使用规范和完整性保护算法(128-EIA3) 使用规范. 在5G R15 版本标准制定过程中, 3GPP 中国参会企业代表与ETSI SAGE、GSMA 等共同对128-EEA3/EIA3 标准进行了修订, 将ZUC-128 算法作为5G 空口机密性和完整性保护算法(128-NEA3/NIA3) 推进成为了5G 标准. 随着量子计算不断发展, 在2017 年3GPP 安全组(SA3) 的会议上, 多个企业提出了5G 中使用256 比特对称密码算法的需求. 为此, 3GPP SA3 专门开展研究项目, 探讨256 比特密码算法在5G 中应用相关问题[3]. 在研究项目中, 空口机密性和完整性保护算法是各国企业关注的重点: 美国AT&T 等公司提出未来5G 标准应当使用AES-256 算法, 提供抗量子计算攻击的能力; 我国于2018 年初公布了使用256 比特密钥、基于ZUC-128 算法设计的ZUC-256 序列密码算法(草案)[4]; 欧洲爱立信等公司在2018 年底提出了256 比特的SNOW-V 序列密码算法[5]. 与128 比特密钥的ZUC-128 算法相比, ZUC-256 算法对初始化进行了重新设计, 增加了初始化向量(IV) 长度以提供足够的安全冗余; 能够支持多种长度的消息认证码(MAC), 以应对5G 潜在的多安全级别的需求. 除了安全性, 空口密码算法在终端芯片和网络侧设备中实现性能、对于现有设备的影响(如升级、改造成本影响), 也是3GPP 重要考察指标. 由于AES-256 算法与现阶段标准化的AES-128 算法(128-NEA2/NIA2) 相比仅增加了轮数, 因此对于终端芯片设计的影响非常小; 在网络侧无论是使用专用硬件实现还是基于通用服务器虚拟化实现(如使用Intel X86 架构CPU 的通用服务器, 可以利用Intel专门的指令集进行加速), 性能都能够满足5G 需求. 欧洲爱立信公司提出的SNOW-V 算法复用了AES轮函数的结构, 在网络侧进行通用服务器虚拟化实现时, 能够直接使用AES 算法的全部指令集, 加解密速度高于AES; 但是在终端芯片中很难复用已有硬件. ZUC-256 算法主体结构与ZUC-128 相同, 对于终端十分友好; 但是Intel 处理器没有专门针对ZUC-128 算法设计指令集, 因而ZUC-256 算法在通用服务器上性能能否满足5G 通信加密标准的高速要求, 即在纯软件实现条件下达到20 Gbps 的下行速度[6], 成为了标准推进中的关键问题.
截至目前, 国内外学者对ZUC-128 算法实现的研究主要集中在其硬件FPGA 实现[7–11]以及在高通Hexagon DSP 架构上的软件优化[12–14]. 然而, 公开的文献中ZUC-128 的软件实现方法仅限于查表实现, 受限于密钥流生成阶段的查表运算, ZUC-128 算法在软件上的性能表现并不太理想. ZUC-256 算法作为ZUC-128 算法的升级版本, 也面临着相同的困境. 2008 年3 月, Intel、AMD 处理器厂商宣布在其x86 架构处理器上推出用于AES[15,16]加/解密运算的AES-NI 指令集[17], 采用AES-NI 指令集的单指令多数据(Single Instruction Multiple Data, SIMD) 技术[18,19]实现AES 算法的软件实现性能是采用查表方法的3.5 倍. 近些年来, 随着SIMD 技术的不断完善, 它的高效软件实现性能使得越来越多的密码算法将其应用到软件实现上, 例如2012 年, Seiichi 和Shiho[20]将SSE 指令结合bit-slice 技术[21]应用到PRESENT[22]和Piccolo[23]算法上, 使二者实现吞吐量分别达到4.73 和4.57 cycle/byte; 2013 年Neves 和Aumasson[24]将AVX2 指令集应用到杂凑密码算法SHA-3 的候选算法BLAKE[25]上并提高了其实现性能. 因此, 利用SIMD 技术快速软件实现ZUC-256 算法成为重要研究内容. 不久前, 以色列的两位学者利用AES-NI 指令集对ZUC-256 的密钥流生成算法的查表运算进行软件优化, 速度提升了4.5倍; 其核心思想是直接从ZUC-256 的S-盒的数学逻辑结构入手, 利用查表指令和AES-NI 指令集实现多路并行计算, 从而完全避免建大表[26]. 但是, 文献[26] 中仅给出了ZUC-256 的密钥流生成算法的快速软件优化实现方法, 并没有给出MAC 生成算法的软件优化实现方法.
本文主要的工作是对ZUC-256 的软件实现进行整体优化, 包含密钥流生成算法和MAC 生成算法.对于密钥流生成算法, 我们对文献[26] 中的密钥流生成算法实现方法进行优化, 包括S-盒查表方法以及向量转换的优化等; 对于MAC 生成算法, 我们将文献[12] 中对ZUC-128 的软件优化技术, 包括延迟模约方法和构造泛哈希函数方法, 推广到了ZUC-256 的MAC 生成算法中. MAC 生成算法的软件实现主要有两大瓶颈需要突破, 一是明文消息的比特判断, 二是密钥流每次只能进行“1-比特” 运算. 对于前者我们利用SIMD 技术中的比较指令来规避比特判断, 据我们所知, 我们是第一个将这种想法应用到序列密码之中的, 但是这种方法依旧无法实现每次按字操作计算. 从MAC 生成算法的设计角度来看, 密钥流和明文消息可以看成是一个GF(2m) 域上的线性泛哈希函数[27], 而这刚好是MAC 生成算法的核心. 2010 年,英特尔推出的一个新的指令, 无进位乘法指令PCLMULQDQ, 它最大的特点是支持GF(2m) 域上的乘法,该指令常常被用于信号处理、有限域、纠错码和密码学中. 对于密码学, 以前的一些研究结果表明可以利用无进位乘法指令来有效实现许多密码算法, 包括但不限于: AES-GCM 中的GHASH 算法[28]、二元域上的椭圆曲线[29,30]以及Koblitz 曲线中的椭圆曲线[31]. 同传统的GF(2m) 域上的乘法相比, 无进位乘法指令在软件实现上有着非常明显的速度提升. 我们利用PCLMULQDQ 指令将MAC 生成中的比特滑动异或转化为GF(2m) 上的多项式乘法运算, 达到了每次按字计算而非比特计算的快速软件实现目标, 速度至少可以提升2.5 倍[12].
本文探讨ZUC-256 流密码算法在x86 架构处理器上的软件优化实现方法, 将SIMD 技术的并行性应用到ZUC-256 的软件优化实现中. 实验结果表明, 与目前基于查表实现密钥流生成的方法相比, 利用SIMD 技术的软件实现性能具有明显优势; 此外利用无进位乘法指令实现MAC 生成可以做到每次按字操作.
本文的结构如下: 首先第2 节概述预备知识, 简要介绍ZUC-256 算法流程. 接下来第3 节利用SIMD技术实现密钥流生成算法以及实现MAC 生成算法. 在第4 节, 我们对第3 节中的方法进行优化以及将其他一些优化方法应用到ZUC-256, 并对比测试结果. 最后第5 节对本文做一个总结.
2 预备知识
本节首先介绍一些符号定义, 然后简要介绍ZUC-256 算法.
2.1 符号定义
下面介绍后文将要使用到的符号定义.

下文中的十六进制值均以前缀0x 表示(如0x3B 为十进制的59).
2.2 ZUC-256 密钥流生成算法
ZUC-256 算法的完整描述在文献[4] 中, ZUC-256 密钥流生成算法包括两个阶段: 初始化阶段和密钥流生成阶段, 这两个阶段操作相似. 每个阶段都包含三个部分:
(1) LFSR. 496-比特长的线性反馈移位寄存器, 由16 个31-比特记忆单元变量{s15,s14,··· ,s0}构成, 这些单元均定义在集合{1,2,··· ,231−1}上;
(2) BR. 比特重组层, 从LFSR 层中抽取一些内部状态, 并拼接成4 个32-比特字{X0,X1,X2,X3};
(3) FSM. 有限状态自动机, 输入由BR 层决定, 包含2 个32-比特字R1与R2作为FSM 中的记忆单元变量.
令p=231−1, Hp={1,2,··· ,p}为不大于p的所有正整数集合. 定义LFSR 反馈函数F1:H5p →Hp为以下函数:


(1)X0:=FH(s15≪1)||FL(s14),X1:=FL(s11)||FH(s9≪1),X2:=FL(s7)||FH(s5≪1),X3:=FL(s2)||FH(s0≪1).
(2)Z:=((X0⊕R1)⊞R2)⊕X3,W1:=X1⊞R1,W2:=X2⊕R2.
(3)R1:=S(L1(FL(W1)||FH(W2))),R2:=S(L2(FL(W2)||FH(W1))).
(4)s16:=F1(s0,s4,s10,s13,s15).
(5){s0,s1,··· ,s15}:={s1,s2,··· ,s16}.
(6) 返回密钥流字Z.
在初始化阶段, 密钥载入过程首先将一个256-比特的种子密钥SK 和一个184-比特的初始向量IV 打入到LFSR 的记忆单元变量{s15,s14,··· ,s0}中作为其初始状态; 其次, 令非线性函数F的两个记忆单元变量R1和R2为0; 最后运行初始化迭代过程32 次, 完成密钥载入过程. ZUC-256 密钥流生成算法在完成初始化阶段以后, 依次执行LFSR 层、BR 层和FSM 层进行状态更新, 完成一次迭代过程, 在此过程中不输出任何密钥流字, 随后进入到密钥流的输出过程.
2.3 ZUC-256 MAC 生成算法

(2) 初始化Tag:=(z0,z1,··· ,zt−1).
(3) 当i=0 到l −1 时执行:
(3.1)Wi:=(zt+i,zt+i+1,··· ,z2t+i−1);
(3.2) 若mi=1, 则Tag=Tag⊕Wi.
(4)Wl:=(zl+t,zl+t+1,··· ,zl+2t−1).
(5) Tag=Tag⊕Wl.
(6) 返回Tag 作为MAC 输出.
在MAC 生成阶段, 为了防止伪造攻击, 对于不同长度的认证标签, 在初始化阶段所采用的常数均不相同, 同时也异于ZUC-256 密钥流生成算法中采用的常数.
3 基于x86 平台上的SIMD 技术并行实现ZUC-256
SIMD 最大的优点在于它的并行性, 该技术可实现同一操作并行处理多组数据. 目前支持SIMD 技术的处理器厂商主要有Intel、AMD、ARM 等, Intel 处理器中的SSE/AVX 指令集及AMD 处理器中的SSE/XOP 指令集中的指令均采用SIMD 技术, 大多数PC 及服务器采用的是Intel 处理器. 本文使用的是基于Intel 处理器的SIMD 并行技术.
SIMD 技术可用于并行计算, 寄存器的长度有128 比特(SSE 系列)、256 比特(AVX2) 和512 比特(AVX512), 使用SIMD 技术对ZUC-256 算法进行优化的点主要是考虑可以并行计算逻辑运算、查表运算和模加运算等. 由于ZUC-256 中计算的基本单元为32-比特的字, 因此, 除了建大表, 对单密钥或单IV模式(不使用SIMD 进行并行计算的算法实现模式) 的优化基本不可行. 以下针对ZUC-256 的优化均为多密钥或多IV 模式下的优化.
(1) 对于支持128-比特寄存器的系统(SSE), 可以并行处理4 条数据的运算操作;
(2) 对于支持256-比特寄存器的系统(AVX2), 可以并行处理8 条数据的运算操作;
(3) 对于支持512-比特寄存器的系统(AVX512), 可以并行处理16 条数据的运算操作.
接下来我们通过利用SIMD 技术分别优化实现ZUC-256 的密钥流生成算法和MAC 生成算法.
3.1 密钥流生成算法的SIMD 实现
从ZUC-256 密钥流生成算法的描述可知, 在FSM 层需要用到两个8-比特的S-盒对32-比特的字进行四次查表运算. 在单密钥模式中, 我们可以通过建大表以空间换时间的方式快速实现查表运算, 但如果在多密钥模式中使用SIMD 技术并行处理多条数据, 即使建大表也不能实现多条数据并行查表运算操作,打破了SIMD 的并行性. 因此如何利用SIMD 技术既能快速实现ZUC-256 算法又能继承其并行性是我们整个工作的核心. 在本节中我们收集归纳了几种ZUC-128 和ZUC-256 的优化方法, 并将ZUC-128 的优化方法适当推广到ZUC-256 中, 最后分析其优缺点和可行性.
3.1.1S0-盒的SIMD 实现[26]
S0为3 个4 比特变换P1、P2和P3(见表1) 通过3 轮Feistel 结构迭代产生,S0-盒的结构图具体见图1.

表1 S0-盒查表运算中P1/2/3 变换Table 1 P1/2/3 maps used during S0 S-box algorithm
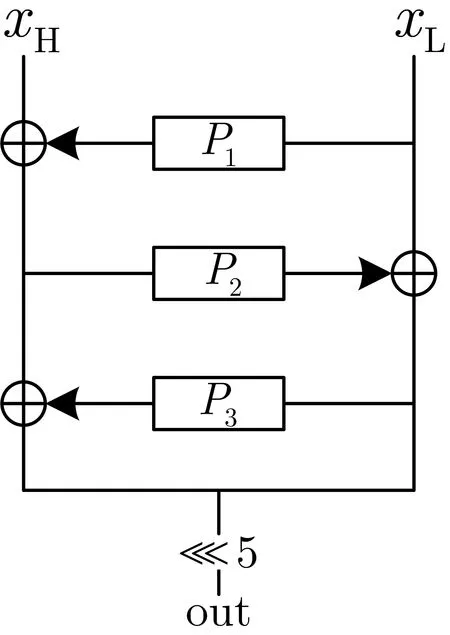
图1 S0-盒结构Figure 1 Algebraic structure of S0-box
令x为8-比特字节输入, 令xL、xH分别为其低4-比特和高4-比特, 以下为S0-盒的实现详解.
(1)t=P1[xL]⊕xH;
(2) outL=P2[t]⊕xL;
(3) outH=P3[outL]⊕t;
(4) out = out ≪5;
(5) 返回out.
为了利用 SIMD 技术实现P1、P2和P3变换, 可以借助字节查表指令 PSHUFB, SSE 中的_mm_shuffle_epi8 (AVX2 中的_mm256_shuffle_epi8 以及AVX512 中_mm512_shuffle_epi8), 该指令接受两个16-字节(或32-字节或64-字节) 的向量: 以第一个向量map 作为表, 第二个向量mask中的元素作为索引值进行查表得到一个16-字节(或32-字节或64-字节) 的向量. 例如: 令mask={15,14,··· ,0},则_mm_shuffle_epi8(P1,mask)={9,3,··· ,9}为P1的反序.算法1展示了利用AVX2实现S0-盒的具体过程(SSE 与AVX512 类似).

算法1 ZUC-256 S0输入: 32-字节向量in输出: 32-字节向量out定义: byte_low4_mask = _mm256_set_epi8(0x0F)定义: byte_hi3_mask = _mm256_set_epi8(0xE0), byte_low5_mask = _mm256_set_epi8(0x1F)定义: p1_mask = _mm256_set_epi32(0x09030507,0x0C000400,0x0A020F0F,0x0E000F09)定义: p2_mask = _mm256_set_epi32(0x0209030F,0x0A0E010B,0x040C0007,0x05060D08)定义: p3_mask = _mm256_set_epi32(0x0D0C0900,0x050D0303,0x0F0A0D00,0x060A0602)1. 程序S0(in)2. hi = _mm256_and_si256(_mm256_srli_epi32(in, 4), byte_low4_mask);3. low = _mm256_and_si256(in, byte_low4_mask);4. r = _mm256_xor_si256(hi, _mm256_shuffle_epi8(p1_mask, low));5. s = _mm256_xor_si256(low, _mm256_shuffle_epi8(p2_mask, r));6. t = _mm256_xor_si256(r, _mm256_shuffle_epi8(p3_mask, s));7. tmp = _mm256_or_si256(s, _mm256_slli_epi32(t, 4));8. low = _mm256_and_si256(_mm256_srli_epi32(tmp, 3), byte_low5_mask);9. hi = _mm256_and_si256(_mm256_slli_epi32(tmp, 5), byte_hi3_mask);10. out = _mm256_or_si256(low, hi);11. 返回out.
需要说明的是_mm256_set_epi32 指令只允许8 个32-比特的字作为输入, 按先高位后低位的顺序排列,算法1中的p1_mask、p2_mask 和p3_mask 应当分别输入两次P1、P2和P3的值(AVX512 需要输入四次), 即p1_mask = _mm256_set_epi32(0x09030507, 0x0C000400, 0x0A020F0F, 0x0E000F09,0x09030507, 0x0C000400, 0x0A020F0F, 0x0E000F09), 因此在实际的C 代码中需要输入两次. 在这里由于篇幅原因,算法1中只输入了一次, 下文中情形类似.
3.1.2S1-盒的SIMD 实现[26]
从2.2 节可知,S1是基于有限域GF(256) 上的逆函数构造的, 与分组密码AES 的S-盒类似, 它们之间仿射等价. 记FAES表示模本原多项式fAES(x)=x8+x4+x3+x+1 的有限域GF(256), AES 算法的S-盒(记为SAES) 的构造为:SAES(x)=A·x−1+D, 其中A为二元矩阵,D=0x63; 同时记FZUC表示模本原多项式fZUC(x) =x8+x7+x3+x+1 的有限域GF(256),S1-盒的构造为:S1(x) =M ·x−1+B,其中B=0x55,M为二元矩阵. 二元矩阵A和M具体如下:
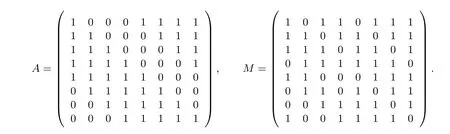
由于S1-盒的构造和SAES-盒的构造是仿射等价的, 因此, 存在一个域FZUC到域FAES的同构映射φ,

其中,K为一个二元可逆矩阵, 文献[26] 中给出了一种计算矩阵K的方法. 因此在同构映射φ下对任意的x ∈FZUC都存在唯一的y=Kx ∈FAES, 通过利用AESENCLAST 指令来计算y−1∈FAES, 最后乘以K−1便可得到x−1∈FZUC, 这样便可以通过AES-NI 指令集来达到实现并行查S1的目的. 首先将SAES-盒转化为:
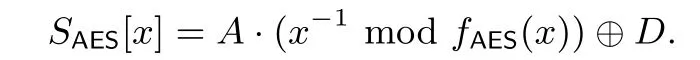
同时,S1-盒:

在同构映射φ下, ZUC-256 算法的加密S1-盒可以等价的构造为:
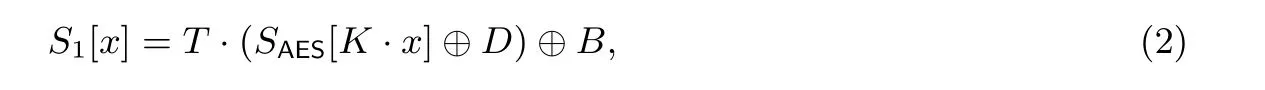
其中T=M·K−1·A−1, 根据文献[26] 给出的方法计算矩阵K,K共有8 种选择, 在这里选择以下的K值, 同时矩阵T也可以被同步计算出来.
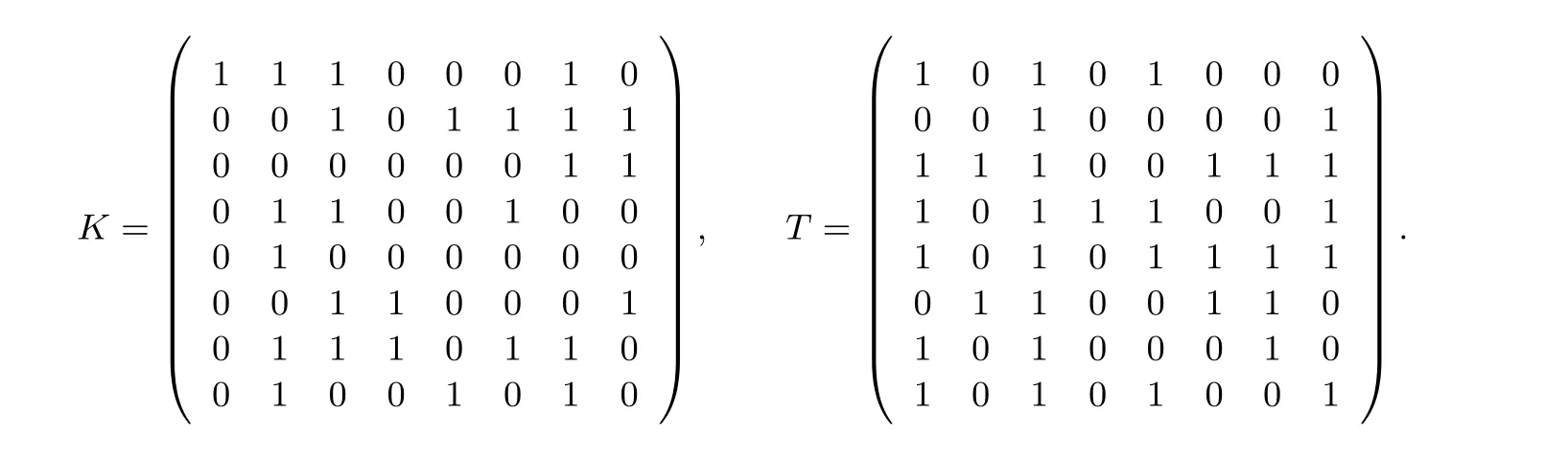
公式(2)中的S1-盒的计算可以分解为矩阵乘法、SAES-盒查表以及异或运算, 而矩阵乘法可以转换为2次查表(4 进8 出) 和1 次异或运算, 以下为S1-盒的实现详解.
(1) 计算y,K1,K2.

(2) 计算z=SAES[y]⊕D, 使用AESENCLAST 指令时需要注意行移位变换;
(3) 计算w,T1,T2.

AESENCLAST 指令用于实现分组算法AES 的最后一轮函数, 包括: 行移位变换、字节替代即SAES、轮密钥加. 对上述步骤(2) 中的y进行逆行移位变换以及将轮密钥置为D, 利用AESENCLAST 指令便可得到z进而计算出S1.算法2为S1-盒用AVX2 实现的具体过程(SSE 与AVX512 类似).

算法2 ZUC-256 S1输入: 32-字节向量input输出: 32-字节向量output定义: k_mask1 = _mm256_set_epi32(0xD3D20A0B,0xB8B96160,0xB3B26A6B,0xD8D90100)定义: k_mask2 = _mm256_set_epi32(0x29AB63E1,0xEE6CA426,0x0F8D45C7,0xC84A8200)定义: t_mask1 = _mm256_set_epi32(0x5B867FA2,0xA479805D,0x538E77AA,0xAC718855)定义: t_mask2 = _mm256_set_epi32(0x47DE73EA,0x33AA079E,0xD940ED74,0xAD349900)定义: aes_row_invshift = _mm256_set_epi32(0x0306090C,0x0F020508,0x0B0E0104,0x070A0D00)定义: aes_cancelkey = _mm_set_epi8(0x63)1. 程序S1(input)2. low = _mm256_shuffle_epi8(k_mask1, _mm256_and_si256(input, byte_low4_mask));3. hi = _mm256_shuffle_epi8(k_mask2, _mm256_and_si256(_mm256_srli_epi32(input, 4),byte_low4_mask));4. tmp = _mm256_shuffle_epi8(aes_row_invshift, _mm256_xor_si256(hi, low));5. tmp = _mm_aesenclast_si128(tmp, aes_cancelkey);6. low = _mm256_shuffle_epi8(t_mask1, _mm256_and_si256(tmp, byte_low4_mask));7. hi = _mm256_shuffle_epi8(t_mask2, _mm256_and_si256(_mm256_srli_epi32(tmp, 4), byte_low4_mask));8. output = _mm256_xor_si256(low, hi);9. 返回output.
注意在算法2中步骤5 和6 只允许接收16-字节的输入, 这是因为Intel 目前只给出16-字节的AES-NI 指令集, 因此当使用AVX2 和AVX512 指令集时分别需要调用2 次和4 次AESENCLAST 指令,单次查S1-盒的效率会比SSE 低, 但是对比经典查表方法这依然是非常高效的.
3.1.3 延迟模约[12]
在计算LFSR 时,为了保证公式(1)的正确性,需要对(1)式中的每次乘法和加法结果进行模约运算. 文献[12] 中提出延迟模约方法对单密钥模式下的ZUC-256 密钥流生成算法进行优化, 其主要思想是: 模数p= 231−1 对于加法模约运算是非常快速的, 只需要用到与运算和移位运算(对任意x,y,z ∈Hp,k ∈Z,k=x+y, 则z=x+ymodp= (k& 0x7FFFFFFF)+(k ≫31)), 但乘以一个2 的幂的乘法模约运算需要用到循环运算, 这对软件优化来说需要更多开销, 如何减少乘法模约运算?
令k ∈Z, 则k=(1+28)s0+220s4+221s10+217s13+215s15的计算是在整环Z 上的乘法和加法,没有模约处理, 很明显k< 222·231=253; 然后计算k′=(k& 0x7FFFFFFF)+(k ≫31)<232−2, 只需要对k′再进行一次加法模约处理可以得到kmodp, 因此计算公式(1)整个过程只需要两次加法模约,在单密钥模式下, 如果需要, 还可以使用汇编语言提升速度.
然而, 若在公式(1)中应用延迟模约方法, 需要将32 位上的加法和乘法操作对应转换到64 位上, 这对于多密钥模式来说需要较大开销(例如: 对于一个8×32-比特的向量, 将其转换为8×64-比特的向量, 则需要两个256-比特的向量进行存储以及其它操作, 最后再将其转为一个8×32-比特的向量), 经过测试, 在多密钥模式应用延迟模约比乘法模约运算开销更大. 因此, 延迟模约技术适合应用到单密钥模式(如果不使用汇编, 对比乘法模约, 提升幅度也并不高), 在多密钥模式下, 使用乘法模约开销会更少.
3.2 MAC 生成算法的SIMD 实现
利用SIMD 技术并行实现MAC 生成算法首先需要解决两个问题, 一是明文消息的比特判断, 二是密钥流每次只能进行“1-比特” 运算. 在本节中, 我们给出了MAC 生成算法的两种SIMD 实现方法.
3.2.1 利用比较指令生成MAC 的SIMD 实现
2.3 节描述了MAC 的生成, 从其描述步骤(3.2) 可知, 每次迭代都需要对明文消息的每1-比特进行判断. 然而, ZUC-256 算法的基本单元都是32-比特的字, 按比特判断不仅会降低软件整体性能, 而且不利于使用SIMD 技术并行处理多条数据, 因此我们的目标是尽量避免明文消息的比特判断以及每次迭代都是按字计算而不是按比特计算. 为了方便描述, 在本文中我们主要针对认证标签长度为32-比特的MAC 生成(64-比特= 2×32 比特, 128-比特= 4×32 比特).
假设生成的密钥比特流为z0,z1,···, 明文比特序列为m0,m1,···, 则2.3 节中MAC 生成描述步骤(3) 中的Wi可以等价转化为Wi=mizi‖mizi+1‖···‖mizi+31. 以下为MAC 生成算法的前32 次迭代的一个等价转换.
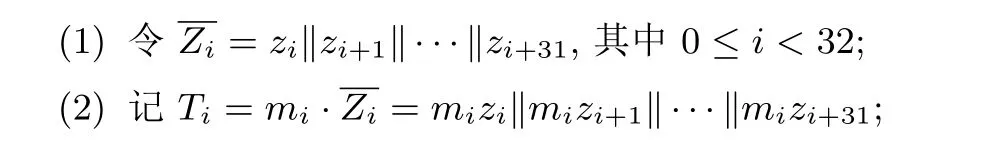
(3) 则Tag=Tag⊕T0⊕T1⊕···⊕T31.
在单密钥模式下, 上述的Ti在本质上依旧避免不了对明文序列的判断, 但是在多密钥模式下, 我们可以利用比较指令PCMPGTD 来很好的规避这一问题,算法3展示了利用AVX2 中的PCMPGTD 指令生成32-比特Tag 的部分过程, 对应2.3 节中的描述步骤(3).

算法3 ZUC-256 MAC 生成算法-1输入: 32-字节向量密钥流组∗vecz, 8×L 个32-比特明文数组∗msg输出: 32-字节向量vtag定义: V2ZERO = _mm256_setzero_si256()1. 程序MAC_Generate(vecz, msg)2. i 从0 到L −1 依次执行:3. r = _mm256_loadu_si256(msg + 8×i);4. j 从0 到31 依次执行:5. s = _mm256_slli_epi32(r, j); t = _mm256_cmpgt_epi32(V2ZERO, s);6. u = _mm256_srli_epi32(vecz[i+2], 32 −j);7. v = _mm256_slli_epi32(vecz[i+1], j); w = _mm256_or_si256(u, v);8. vtag = _mm256_xor_si256(vtag, _mm256_and_si256(w, t));9. vtag = _mm256_xor_si256(vtag, tmp); tmp = vtag;10. 返回vtag.
算法3的主要思想是利用_mm256_cmpgt_epi32(a, b) 的输出结果, 该指令接受两个256-比特的向量, 按有符号的32-比特进行比较, 大于输出0xFFFFFFFF, 否则输出0; 因此将明文消息字进行左移, 然后与0 进行比较, 如果移位后的明文消息字最高位为1, 则为负数, 经过比较指令后输出0xFFFFFFFF,再经过与运算就可以取出Wi.
3.2.2 利用无进位乘法指令生成MAC 的SIMD 实现
算法3中虽然利用PCMPGTD 比较指令规避了明文序列的判断, 但是在步骤7 中的或运算等价于在密钥比特流上按比特滑动, 这类似于字循环操作, 并不利于软件优化; 除此之外, 在步骤4 中仍然需要执行32 次才能处理一个明文消息字, 换句话说, 这在本质上是按比特计算, 依然没有达到真正意义上的按字计算. 文献[12] 给出一种方法, 在单密钥模式下利用无进位乘法指令PCLMULQDQ 来快速生成ZUC-128的MAC, 可以每次迭代处理一个明文消息字. 与ZUC-128 流密码中的MAC 生成算法相比, ZUC-256 在算法结构上并没有太大的改变, 因此我们可以将文献[12] 中的方法推广到ZUC-256 的MAC 生成算法的多密钥模式中, 并优化了其方法中的某些步骤, 以此加速其实现进程.
假设生成的密钥比特流为z0,z1,···, 明文比特序列为m0,m1,···, 则密钥比特流和明文序列可以看做是一个F2[x] 上的线性泛哈希函数的输入. 2010 年, Intel 在他们的32 纳米处理器家族上引进了一种新的指令PCLMULQDQ; 令人感到惊喜的是, 该指令可以计算两个64-比特数的无进位乘法乘积, 即计算两个在F2[x] 上次数最多为63-次的二元多项式的乘积(最多为126-次的多项式). 在实现性能方面,PCLMULQDQ 能够在14 个时钟圈内执行, 这远快于经典的F2[x] 上的多项式乘法运算. 因此我们可以利用无进位乘法指令PCLMULQDQ 来计算MAC 生成. 下面我们展示如何利用PCLMULQDQ 指令快速生成MAC, 首先我们将2.3 节MAC 生成描述步骤(3) 中前32 次计算等价转换为另一种描述.
(1) 令r=(m31,m30,··· ,m0)T;
(2) 令 矩阵
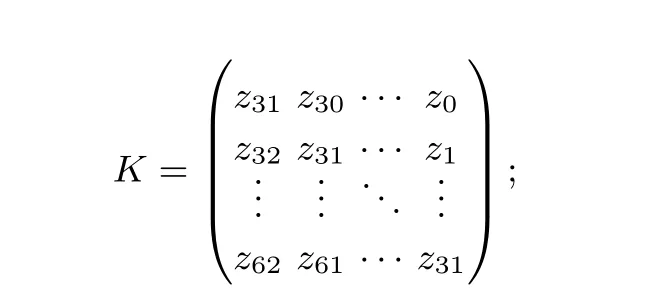
(3) 则Tag=Tag⊕(K·r).
注意K · r是在域F2上进行的, 即操作运算中的加法为异或运算. 令m,p,p1,p2,q ∈F2[x],m=m0+m1x+···+m31x31为F2[x] 上的一个31-次多项式, 其序和第一个明文消息字的序相反;p1=z31+z30x+···+z0x31为第二个密钥流字作为F2[x]上的一个31-次多项式;p2=z63+z62x+···+z32x31为下一个密钥流字;p=p1x32+p2为两个密钥流字构成的63-次多项式;q=mp=q2x64+q1x32+q0为多项式m和p的乘积, 我们将证明q1(一个32-比特的字, 作为多项式的系数) 和K·r是等价的.

因此MAC 的生成运算可以等价转化为F2[x] 上的多项式乘法. 在实际的软件实现中, 首先将消息字的反序(将反序结果转换为64-比特, 高32 位为0) 和两个32-比特密钥流字作为PCLMULQDQ 指令的输入, 取出其运算结果中的q1便可得到K ·r. 对后续的所有明文消息字重复同样的步骤直到我们获得最终的MAC 码, 达到了每次按字计算而非比特计算的快速软件实现目标.算法4为AVX2 中的PCLMULQDQ 指令生成32-比特Tag 的实现过程.
在算法4中, PCLMULQDQ 指令需要输入两个128-比特向量以及一个控制选择位, 该指令根据控制选择位每次选取两个128-比特向量中某两个64-比特数计算得到一个128-比特向量, 这在AVX2 和AVX512 中需要多次调用才能得到结果, 其效率会比SSE 低. 除此之外, 在步骤3 中还需要对明文序列字进行反序处理, 目前SIMD 技术在x86 平台上还没有提供比特反序的指令, 如果未来Intel 提供比特反序的指令, 利用PCLMULQDQ 指令会有更进一步的优势.
4 方案优化与试验结果
在本节中我们将第3 节中的技术应用到ZUC-256 算法中, 并对其中一些技术方法做进一步的优化;在4.4 节中我们对比几种不同方法实现ZUC-256 流密码算法的软件性能, 并分析其结果. 我们已将完整的C 实现代码(AVX512 版本) 公开发布在GitHub 网站上: https://github.com/Nonights/ZUC256.
4.1 S-盒优化

算法4 ZUC-256 MAC 生成算法-2输入: 32-字节向量密钥流组vecz, 8×L 个32-比特明文数组msg输出: 32-字节向量vtag (8 个并行的32-比特Tag)1. 程序MAC_Generate(vecz, msg)2. i 从0 到L −1 依次执行:3. r = Word_reverse(_mm256_loadu_si256(msg + 8×i)); /∗对每一路消息字进行反序处理∗/4. s[4] = Expandtovec128(r); /∗将r 的每路数据扩展为64 比特并转换成4 个SSE 中的向量∗/5. w[4] = Storetovec128(vecz[i+1], vecz[i+2]); /∗将两个密钥流向量转换成4 个SSE 中的向量∗/6. j 从0 到3 依次执行:7. u[j] = _mm_clmulepi64_si128(s[j], w[j], 0x00);8. v[j] = _mm_clmulepi64_si128(s[j], w[j], 0x11);9. tmp = Loadtovec256(u[4], v[4]); /∗取出每路中的q1 并生成一个32-字节向量∗/10. tmp = _mm256_xor_si256(tmp, temp); temp = tmp; /∗更新tmp, temp 的初始值置为0 ∗/11. vtag = _mm256_xor_si256(_mm256_xor_si256(vecz[0], tmp), vecz[L+1]);12. 返回vtag.
在第3 节中,算法1和算法2的输入输出均为32-字节的向量(针对AVX2), 然而回顾ZUC-256 算法描述中对于查表操作S(Y3||Y2||Y1||Y0) =S0(Y3)||S1(Y2)||S0(Y1)||S1(Y0), 即在单密钥模式下,S0-盒只对字Y的奇字节位进行查表, 而S1-盒只对字Y的偶字节位进行查表; 换句话说, 在多密钥8×32 模式下, 对于一个32-字节的向量vecs,S0和S1只需要分别对其奇字节位和偶字节位进行查表. 第一种方法是利用算法1和算法2先分别计算出S0(vecs) 与S1(vecs), 然后再分别取出奇字节和偶字节, 最后再移位异或得到S(vecs); 然而以这种方法查表计算, 会浪费很多开销, 因为S0不需要对vecs中的偶字节位进行查表, 同理S1也不需要对vecs中的奇字节位进行查表. 第二种方法如下: 在单密钥模式下, 假设R1=S(X3||X2||X1||X0) =S0(X3)||S1(X2)||S0(X1)||S1(X0),R2=S(Y3||Y2||Y1||Y0) =S0(Y3)||S1(Y2)||S0(Y1)||S1(Y0), 则令R′1=S0(X3||Y3||X1||Y1) =S0(X3)||S0(Y3)||S0(X1)||S0(Y1),R′2=S1(X2||Y2||X0||Y0) =S1(X2)||S1(Y2)||S1(X0)||S1(Y0), 最后再通过移位、与和异或便可得到R1和R2, 避免不必要的开销. 除此之外, 在使用第二种方法实现S时, 还可以利用混合指令VPBLENDVB和移位指令VPSLLD (或VPSRLD) 进一步优化实现,算法5为2.2 节里描述步骤(3) 中R 的AVX2 实现(SSE 和AVX512 类似).

算法5 ZUC-256 R输入: 32-字节向量l1, l2输出: 32-字节向量r1, r2定义: even_byte_mask = _mm256_set1_epi32(0x00FF00FF)1. 程序R(l1,l2)2. a = S0(_mm256_blendv_epi8(l1, _mm256_srli_epi32(l2, 8), even_byte_mask));3. b = S1(_mm256_blendv_epi8(_mm256_slli_epi32(l1, 8), l2, even_byte_mask));4. r1 = _mm256_blendv_epi8(a, _mm256_srli_epi32(b, 8), even_byte_mask);5. r2 = _mm256_blendv_epi8(_mm256_slli_epi32(a, 8), b, even_byte_mask);6. 返回r1, r2.
4.2 向量转换优化
目前, Intel 只提供了AESENCLAST 和PCLMULQDQ 的SSE 指令, 即只允许128-比特的运算操作,因此当使用AVX2 和AVX512 时分别需要调用2 次和4 次相应的SSE 指令. 例如在AVX2 指令集中,对于一个256-比特的输入向量vec, 当调用AESENCLAST 指令时, 需要将vec 转换为两个128-比特的向量; 这里有两种转换方法, 一种是利用memcpy 命令或者利用指针进行强制转换, 然而这种方法不是并行处理的. 另一种方法是利用转换、提取和插入指令, 这种方法可以保证算法过程的并行性; 其次对比第一种方法, 后者在多次调用中性能会有明显提升.算法6为算法1中步骤5 的具体AVX2 实现.

算法6 ZUC-256 USE_AES-NI输入: 32-字节向量tmp输出: 32-字节向量tmp 1. 程序USE_AES-NI(tmp)2. _mm256_storeu2_m128i(temp, temp + 1, tmp); /∗temp 为两个128-比特的临时向量组∗/3. temp[0] = _mm_aesenclast_si128(temp[0], aes_concelkey);4. temp[1] = _mm_aesenclast_si128(temp[1], aes_concelkey);5. tmp = _mm256_loadu2_m128i(temp, temp + 1);6. 返回tmp.
算法6中的方法依然可以推广到AVX512, 在AVX512 中需要用到四次512-比特到128-比特向量转换、四次AESENCLAST 指令调用和四次128-比特到512-比特向量转换, 性能相对会进一步下降. 利用SIMD 技术实现MAC 生成时, 调用PCLMULQDQ 指令和AESENCLAST 情形类似, 但是需要注意明文消息的注入(每一路32-比特消息需要进行反序处理并扩展为64-比特, 高32-比特为0) 和密钥流字的顺序.
4.3 LFSR 层的移位操作优化
除了算法本身的优化以外, 还可以通过增加代码的复杂度减少LFSR 层的移位操作来提升性能. 在密钥流生成阶段, 每一轮迭代对BR 层、FSM 层和LFSR 层的状态进行更新, 当明文消息流足够长的时候,代码中for 循环也在增加. 注意到LFSR 层, 每次只对最后一个寄存器的值进行更新, 而其他值都是由后一个寄存器的值覆盖更新, 在16 个迭代中所有值全部被更新, 因此可以通过多轮连续迭代减少移位操作.例如在密钥流生成阶段, 在一个循环内做16 次迭代可以最大程度的减少移位操作.
4.4 试验结果
在本小节中, 我们将测试不同方法的软件实现性能, 分为密钥流生成和MAC 生成两个大类(见表2);注意我们以文献[4] 中的参考代码为基准, 其余实现方法都是在此基础上进行优化. 我们对比文献[12] 中的延迟模约方法、文献[26] 中的SIMD 技术和本文的优化SIMD 技术分别实现ZUC-256 密钥流生成算法的软件性能, 以及对比文献[26] 中的无进位乘法方法、本文中的比较指令(方法1) 和无进位乘法指令(方法2) 的SIMD 技术分别生成MAC 的软件性能.

表2 对比测试版本Table 2 Eight versions of test
我们分别在2 个不同处理器平台上对ZUC-256 的软件实现性能进行评估,一个是Intel(R)Core(TM)i3-6100 CPU @3.70GHz, 该平台有4GB 内存, 系统类型为32 位Win7 操作系统, 记为Platform1; 另一个平台是Intel(R) Xeon(R) Gold 6128 CPU @3.40 GHz, 128 GB 内存, 64 位Win10 操作系统, 记为Platform2. Platform1 和Platform2 分别使用Visual Studio 2015 软件和Visual Studio 2017 软件进行性能测试, 同时两个平台除了算法本身的优化外, 没有对软件进行额外的优化设置, 均使用的是软件默认设置. Platform1 和Platform2 中运行软件的解决方案配置均采用Release 模式, 前者解决方案平台使用x86, 后者使用x64.
表2 中的测试方法均使用C 代码实现, 没有使用汇编语言; 其中文献[4] 和文献[12] 中的四种方法均为在单密钥模式下的软件实现, 而剩余四种方法利用SIMD 技术并行实现. 除此之外, Platform1 中使用的SIMD 技术均为AVX2, Platform2 中的SIMD 技术均为AVX512. 图2、图3、图4 和图5 分别展示了两个不同平台上ZUC-256 密钥流生成和MAC 生成的各个实现方法的软件性能. 评估ZUC-256 密钥流生成算法和MAC 生成算法的软件实现性能指标是算法每秒钟处理数据的比特数, 即bps; 在本文中,1 Gbps = 109bps. 在Platform1 中, 我们将LFSR 层的移位操作优化技巧应用到本文的3 个实现方法中, 和没有增加代码复杂度的实现方法相比, 速度提升了大约15%. 从图2–图5 可以发现, 密钥流生成算法和MAC 生成算法的最优软件实现性能结果均为AVX512 版本, 密钥流生成算法的AVX512 版本实现性能可以达到21 Gbps, 相较于目前已知的最优实现方法[26]性能提升了30%, 而AVX2 版本的实现性能则提升了56%, 主要原因在于编译软件的不断智能化, Visual Studio 2017 对于代码中的类似LFSR 层的移位操作会自行进行优化(注: 由于文献[26] 的参考文献中给出的完整实现代码所在网址无法打开, 我们对比的结果是通过利用文献[26] 中给出的方法然后自行编写的代码运行得出的, 但文献[26] 中结论表示AVX512 版本比AVX2 的实现性能稍差, 这与理论逻辑不符, 并且我们的运行结果也验证了这一点).MAC 生成算法同文献[4] 中的无优化实现方法相比性能提高了20 倍. 在表2 中我们只列举了一部分优化方法的组合对比, 然而某些不在表2 中的其他的优化方法组合可能会有更进一步的速度提升, 在这里我们就不对所有可能的组合进行一一测试.

图2 四种ZUC-256 密钥流生成实现方法在两个平台上的性能表现Figure 2 Performance of four different methods of ZUC-256 crypt on two platforms

图3 四种32 比特MAC 生成实现方法在两个平台上的性能表现Figure 3 Performance of four different methods of 32-bits MAC generation on two platforms

图4 四种64 比特MAC 生成实现方法在两个平台上的性能表现Figure 4 Performance of four different methods of 64-bits MAC generation on two platforms

图5 四种128 比特MAC 生成实现方法在两个平台上的性能表现Figure 5 Performance of four different methods of 128-bits MAC generation on two platforms
5 结论
在本文中, 我们给出了ZUC-256 序列密码算法的整体快速软件实现方法, 包括密钥流生成算法和MAC 生成算法. 密钥流生成算法是基于文献[26] 中提出的方法基础上快速实现的, 我们一方面优化了S-盒的查表操作, 避免了不必要的查表开销; 另一方面, 在调用AES-NI 指令集时, 我们还对向量转换方式进行优化, 保证了SIMD 实现过程的并行性. 实验结果表明, 我们的优化方案和文献[26] 相比软件实现性能具有较大优势, 在Intel(R) Core(TM) i3-610 处理器和Intel(R) Xeon(R) Gold 6128 处理器上的软件实现性能分别提升了56% 和30%, 并且在后者处理器上的软件实现性能可以达到21 Gbps, 超过了5G 系统中的下行速度要求. 由于ZUC-128 算法和ZUC-256 算法中的MAC 生成算法大体结构是一样的, 文献[12] 中构造的无进位乘法方法依然可以应用到ZUC-256 的MAC 生成算法中; 同无优化的MAC 生成算法的软件实现性能相比, 我们利用无进位乘法指令并行实现MAC 的方法具有非常明显的优势. 但是, 在密钥流生成算法和MAC 生成算法中用到的AESENCLAST 指令和PCLMULQDQ 指令目前只允许输入128-比特的向量(SSE), 因此使用AVX2 和AVX512 指令集需要多次调用, 性能会有所降低.Intel 在2019 年5 月发布的白皮书中提出未来要扩展现有的指令集, 尤其是都规划了AESENCLAST 指令和PCLMULQDQ 指令的AVX2 和AVX512 版本[32]. 等到这些指令集正式发布以后, 相信ZUC-256算法的软件实现性能会有更进一步的提升.
