屈曲分析在底盘悬架开发中的应用

张旭，刘大勇

（氢澈科技（天津）有限公司，天津 300380）

前言

强度、刚度及稳定性是材料力学中提到的构件的三要素，但在乘用车底盘悬架开发过程中，一些结构件在受压时由于承载力不足而出现结构失稳，导致结构件的功能失效，这类问题称为屈曲问题。

针对此问题，本文详细阐述了屈曲分析的基本原理和分析方法，研究总结了悬架开发中需要进行屈曲分析的结构件以及对应的屈曲分析方法，对于悬架开发具有较强的指导意义。

1 屈曲分析的基本原理

1.1 屈曲特征值分析

特征值屈曲分析也可以说是线性屈曲分析，与结构的几何刚度矩阵有关。为求解特征值，首先求解线性加载状态{P0}的载荷位移关系，即给定{P0}，求解下列方程：

从而得到：

{u0}=加载{P0}的位移结果；

以及{σ} ={u0}引起的应力结果。

假设位移很小，因此可给出任意状态下（{P}，{u}，{σ}）的增量平衡方程：

其中：

Ke=弹性刚度矩阵；

[Kσ（σ）]= 在应力状态{σ}下计算的初始应力矩阵；

假设特征值是加载的载荷{P0}的线性函数，即：

{P}=λ{P0}

{u}=λ{u0}

{σ}=λ{σ0}

从而得到：

因此，增量平衡方程可写为：

当失稳状态开始时，即承载能力达到极限值，此时{△P}≈0，代入公式（3）可得：

为了公式（4），则有：

求解公式（5）可得到结构在加载状态{P0}下的屈曲特征值λ和屈曲模态，再通过线性计算得到屈曲临界载荷。

求解公式（5）可得到结构在加载状态{P0}下的屈曲特征值λ和屈曲模态，再通过线性计算得到屈曲临界载荷。

1.2 非线性后屈曲分析

在计算非线性屈曲时，采用弧长法（RIKS法）较为合适。弧长法是一种用于得到不稳定或负刚度矩阵问题的数值稳定解的方法，它能够有效地分析结构非线性前后屈曲及屈曲路径跟踪，并方便查看结构件的后屈曲状态，因此也被称之为后屈曲分析，具有较强的工程指导意义。

弧长法属于双重目标控制方法，即在求解过程中同时控制载荷因子和位移增量的步长。

其基本控制方程如下：

其中：

△λ为载荷因子增量数值；

φ为载荷比例系数，用于控制弧长法中载荷因子增量所占的比重；

△l为固定的半径。

在求解过程中，载荷因子增量△λ在迭代中是变化的，下列非线性静力平衡的迭代求解公式中存在n个未知数，即：

i=0,1,2，这样，在弧长法中一共存在n+1个未知数，根据约束方程：

即为附加的控制方程，问题才能得到解答，此时，可以根据φ值得取值分为两种弧长法，其中，φ≠0时的弧长法称为球面弧长法，φ=0时的弧长法称为柱面弧长法[1]。

当承受较大载荷时，材料非线性以及大变形等非线性因素导致结构件并不是在理想屈曲强度处发生屈曲。而特征值屈曲分析是完全线性分析，仅可用来预测理想弹性结构的理论屈曲强度。

因此，特征值屈曲分析通常得到的非保守结果即通过该方式计算得到的临界失稳载荷偏大，不适用于实际工程结构上的屈曲分析。

与特征值屈曲分析相比，非线性屈曲分析考虑了材料非线性及几何非线性，更为符合工程实际，因此，通常采用该方法对结构件进行屈曲分析。

2 二力杆结构屈曲分析

在汽车悬架中，有些受压部件当受到较大压力时，杆件可能由于突然变弯而失去承载能力，影响该部件甚至整个系统的正常工作，如E型多连杆中的控制臂、稳定杆连接杆等，如果屈曲临界不足就容易出现此类问题。

2.1 控制臂屈曲分析方法

如图1所示为某车型后E型多连杆式的后上控制臂，控制臂内点通过衬套与副车架连接，控制臂外点通过衬套与轴节连接。由于这种形式的控制臂所受力矩非常小，因此，可将其近似看作二力杆，主要承受拉压载荷[2-3]。

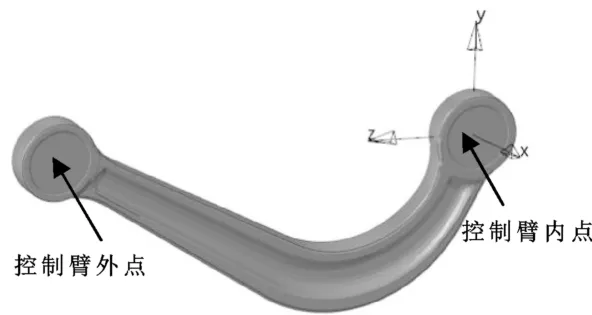
图1 二力杆式控制臂

通过有限元的方法对其进行屈曲分析，在控制臂内点建立局部坐标系，其中X向为轴向方向，Z轴由控制臂内点指向控制臂外点，Y向根据右手定则自动生成，将控制臂内点和控制臂外点均置于该局部坐标系下。

边界条件：约束控制臂内点的1、2、3、6自由度，约束控制臂外点的1、2自由度。

加载方式：在控制臂外点沿局部坐标系Z向负向加载一个足够大的压缩载荷，使得屈曲临界载荷得以复现。

在考虑材料非线性和几何非线性后，采用RIKS法对其求解即可找到屈曲临界载荷点。

2.2 稳定杆连接杆屈曲分析方法

如图2所示为某车型的稳定杆连接杆，两个球头连接点，一端连接在稳定杆上，另一端与轴节连接。与控制臂不同，稳定杆连接杆是真正意义上的二力杆，只承受拉压载荷，而不传递力矩。

图2 稳定杆连接杆

通过有限元的方法对稳定杆连接杆进行屈曲分析，在球头连接点1建立局部坐标系，其中X向为轴向方向，Z向由球头连接点1指向球头连接点2，Y向根据右手定则自动生成。将球头连接点1和连接点2均置于该局部坐标系下。

稳定杆连接杆的屈曲分析方法与二力杆式控制臂相同。

边界条件：约束球头连接点1的1、2、3、6自由度，约束球头连接点2的1、2自由度。

加载方式：在球头连接点2处沿局部坐标系Z向负向加载一个足够大的压缩载荷，使得屈曲临界载荷得以复现。

在考虑材料非线性和几何非线性后，采用RIKS法对其求解即可找到稳定杆连接点的屈曲临界载荷点。

3 前下摆臂屈曲分析

除了主要承受拉、压力的杆件结构外，一些薄壁件在承受较大压力时，也容易发生屈曲，如麦弗逊独立悬架中的前下控制臂的屈曲就属于此类问题。

作为汽车悬架系统中传力和导向的重要部件，其一端通过橡胶衬套与副车架连接，另一端通过球铰与转向节连接，将作用在车轮上的载荷传递给车身，使得车轮能够按照一定轨迹运动，因此，如果前下摆臂失效将直接影响车辆的正常行驶，对其进行屈曲分析很有必要[4-6]。

图3 麦弗逊式独立悬架前下摆臂

在对前下摆臂进行屈曲分析时，约束前下摆臂前、后点的平动自由度，和外点的Z向自由度。

考虑材料和几何非线性后，在前下摆臂外点分别加载X向和Y向载荷，用RIKS法计算分别得到对应方向上的屈曲临界载荷。

4 结论

本文介绍了屈曲分析的基本原理，研究总结了悬架中应着重进行屈曲分析的结构件，包括E型多连杆中的控制臂、麦弗逊式独立悬架中的前下控制臂、稳定杆连接杆等结构，并确定了各结构件对应的屈曲分析方法，对于悬架开发具有重要的指导意义。