基于Logit模型的地铁站台乘客候车区域选择行为研究*

方 勇 王澄斐 胡 华

(上海工程技术大学城市轨道交通学院， 201620， 上海∥第一作者， 讲师)

地铁站台候车乘客在空间上的分布不均衡性会降低站台的乘降效率，对地铁的运营效率与服务水平有直接影响，甚至在高峰时段会诱发站台乘客的安全事故。因此，充分了解地铁站台乘客的候车区域选择行为，建立地铁站台候车乘客的分布模型，对优化站台的设施布局及客流组织均具有重要的理论和实际意义。

目前对城市轨道交通车站站台候车乘客的研究多集中在聚集人数以及客流分布上，而对候车区域选择行为的研究较少。文献[1]计算了不同发车间隔以及上下行列车不同到达间隔的站台聚集人数；文献[2]构建了候车区域乘客分配的函数模型；文献[3]借鉴用户平衡模型，建立了站台上乘客分布的数学模型；文献[4]采用增量分配法对站台候车乘客进行动态分配；文献[5]建立了基于效用函数站台乘客候车路径选择模型；文献[6]基于乘客自身选择特性及候车区域特征建立了乘客候车位置选择的Logit模型。本文在总结已有研究成果的基础上，确定乘客选择候车区域的影响因素，将站台候车区域划分成若干个候车子区域(以下简称“候车子区”)。为简化计算模型，采用Logit模型对站台乘客的候车区域选择行为进行研究。

1 站台候车子区的划分

地铁站台候车乘客的分布受到站台楼扶梯、疏导栅栏、立柱[7]等的影响。此外，站台候车乘客以各车门为中心进行排队候车，因此列车的编组数及车门数对站台候车乘客的分布也会产生影响。一般情况下，站台候车乘客的分布特征在空间上呈现以各站台楼扶梯为中心的分布不均衡性、在相邻车门候车点之间的相对均匀性，且易受站台疏导设施的影响。

本文将地铁站台候车子区定义为在同1个站台候车区域内具有一定交通关联度和交通相似度、面积相近的若干个子区域。本文主要考虑了距离原则[8]和站台候车客流的分布特征，对站台候车区域进行候车子区的划分[9]，以简化计算模型、突出站台候车客流分布特点。以上海轨道交通9号线七宝站为例进行地铁站台候车子区划分，如图1所示。

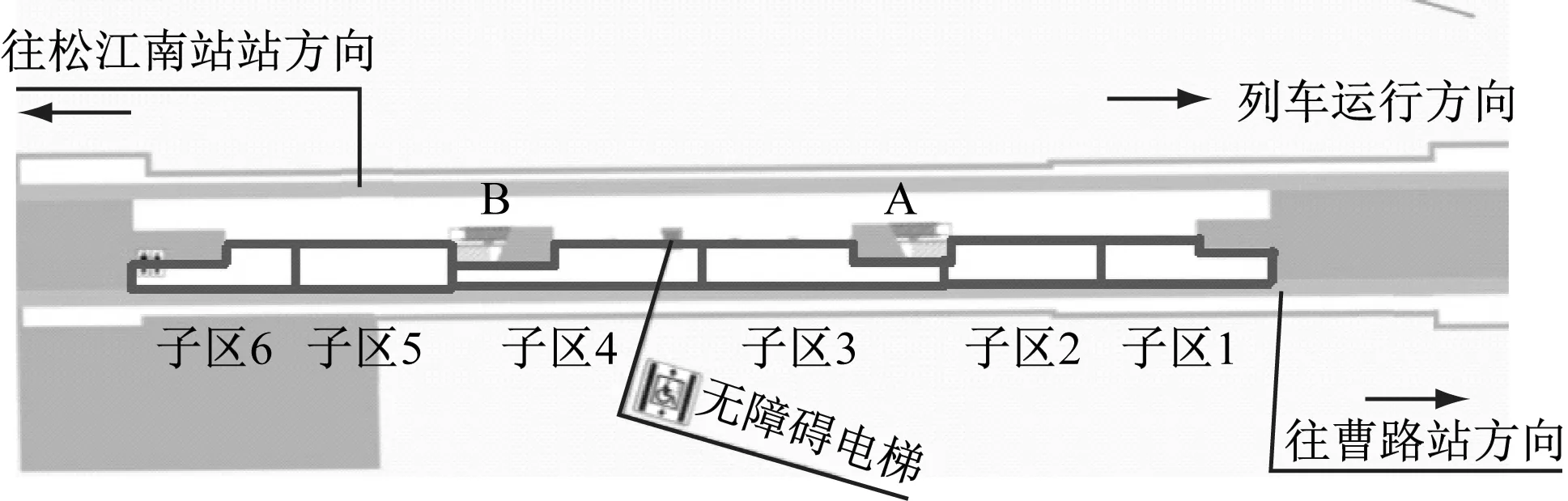
图1 七宝站站台候车子区的划分

候车子区的具体划分方法如下：

1) 由于站台候车乘客以各站台楼扶梯为中心呈现出不均衡分布，本文以各站台楼扶梯的站台入口处作为候车子区的参考分割线，将站台候车区域划分为各站台楼扶梯的前方区域和后方区域。

2) 由于相邻车门候车点处的候车乘客分布具有相对均匀性，本文以1节车厢长度作为候车子区的参考长度，对各站台楼扶梯的前方区域和后方区域进行子区划分，使得各子区之间的长度差异较小。

3) 在站台候车区域内，将列车运行方向的车头处对应的候车子区标号为1，向后依次对各候车子区进行标号。

2 影响因素分析

地铁站台候车乘客以站台楼扶梯为起点，根据自身属性以及周围设施环境条件进行相应的行为选择，最终在某个候车子区内停留，排队候车。乘客对候车子区的选择行为决定了站台候车客流的分布情况，因此需要分析地铁站台乘客候车子区选择的影响因素，提出其指标定义及量化方法。

2.1 乘客至候车子区的距离

如图2所示，以乘客在候车子区2内候车为例，乘客到达站台的起始位置是指乘客所通过的站台楼扶梯与站台连接处的中点位置(点O)，候车子区中心是指该候车子区2条对角线的交点处(点P)。乘客至候车子区的距离是指乘客到达站台的起始位置与各候车子区中心的距离(OP)。一般情况下，候车乘客会更愿意选择离自己距离较近的位置候车。

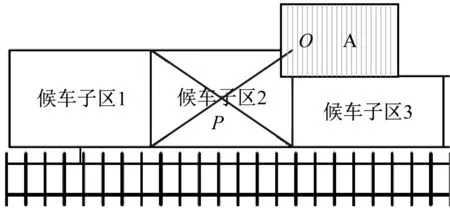
图2 乘客至候车子区的距离示意图

2.2 站台入口处的累计候车乘客数

站台入口处的累计候车乘客数是指从上1班列车驶离车站起，至候车乘客到达站台的时间内，某站台楼扶梯处累计通过的进站乘客数量。一般情况下，站台入口处的累计候车乘客数与该站台楼扶梯附近候车子区内的候车人数成正比。

2.3 候车子区相对乘客拥挤度

候车子区相对乘客拥挤度是指在乘客到达站台时，各候车子区的客流密度与各候车子区的平均客流密度之比。候车子区相对乘客拥挤度与各候车子区的候车人数、子区面积大小有关。若各候车子区的面积相等，则候车子区相对乘客拥挤度就是各候车子区乘客人数与候车子区平均乘客数之比。一般情况下，乘客会倾向于选择乘客拥挤度相对较小的子区作为其候车等待的区域。候车子区i的相对乘客拥挤度可表示为：

(1)

式中：

γi——候车子区i的相对乘客拥挤度；

ρi——候车子区i的客流密度；

ρj——候车子区j的客流密度；

n——站台的候车子区数。

2.4 乘客候车时长系数

乘客候车时长系数是指乘客到达站台时刻与即将抵达的下1班列车到站时刻的时间差与列车发车间隔之比。一般情况下，乘客候车时长系数越小，则乘客到达站台后等待下1班列车到站的时间越短，即乘客对候车子区的选择时空范围越小。乘客候车时长系数可表示为：

r=(t1-t2)/Δt

(2)

式中：

r——乘客候车时长系数；

t1——乘客到达站台的时刻；

t2——乘客到达站台后下1班列车的到站时刻；

Δt——列车发车间隔。

2.5 站台视野度

站台视野度是指乘客到达站台时，候车子区在视野范围内的可视程度。一般情况下，遮挡建筑物数量、乘客至候车子区之间的车门前最大排队人数、乘客与子区的相对距离均与视野度成反比。第i个候车子区的站台视野度可表示为：

ωi=1/(li+qi+mi)

(3)

式中：

ωi——乘客到达站台候车子区i时的视野度；

li——候车子区i与乘客所在候车子区之间相隔的子区数；

qi——乘客至候车子区i之间各车门前的最大排队人数；

mi——乘客至候车子区i之间遮挡建筑物(如楼扶梯、立柱等)的数量。

3 候车子区的选择模型

3.1 前提假设

1) 该模型针对的是从乘客到达站台后至与下1班列车到站的时间段内，站台乘客对候车区域的选择行为问题，且不考虑列车到站后候车乘客根据车厢拥挤情况在邻近候车点的2次选择。

2) 若地铁站台为岛式站台，则将站台候车区域平均分为上行候车区域和下行候车区域，再分别建立候车子区选择模型。

3.2 多项Logit模型

站台候车乘客对候车子区的选择本质是1个离散的选择行为，Logit模型是经典的离散选择模型。由于所研究的站台候车子区选择之间不存在递增或递减的次序关系，因此本文采用无序多项Logit模型[10]。根据效用最大化理论，当候车子区i的效用值Vi大于其他候车子区的效用Vj时，乘客会选择在候车子区i进行候车。

P(y=i)=P[Vi≥Vj]

(4)

式中：

P(y=i)——乘客选择候车子区i时的条件概率值。

式(4)中，设共有n个候车子区，且i≠j，因此i,j的取值范围均为1,2,…,n。式(4)可演变为：

(5)

且满足：

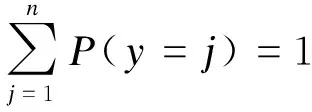
(6)

Vi是乘客对第i个候车子区选择方案的效用值，采用线性加权的形式表示各项影响因素的综合效用值。本文选取最后1个类别作为参照变量，即选取第n个候车子区作为参照变量。Vi的计算公式如下：

(7)

式中：

m——乘客选择候车子区影响因素的总数;

Xk——乘客选择候车子区的第k项影响因素；

βk——模型的回归系数，表示第k项影响因素对乘客选择候车子区的影响权重；

αi——候车子区i的回归截距。

对于不同的候车子区，其模型的回归截距αi和系数βk也不同[11]。本文利用SPSS软件进行多项logistic回归分析，采用极大似然法对参数进行估计，通过似然比检验和伪R方对模型拟合情况进行检验[12]。

4 实例计算分析

本文选取上海轨道交通9号线七宝站下行站台的候车区域为案例，研究站台候车乘客对候车子区的选择行为。七宝站为岛式站台，站台设置2处楼扶梯，列车为6节编组，每节车厢有5扇车门，其中：楼扶梯入口处A(见图1)对应自列车运行方向车头处顺数的第10扇车门，楼扶梯入口处B(见图1)对应自车尾处倒数的第9扇车门。

本文的样本数据来自2019年1月5日7:30—8:30七宝站下行站台候车区域的4个监控视频，共采集1 358名站台乘客对候车子区的选择行为。图3为部分乘客数据采集情况截图。

图3 采集有效样本示例截图

4.1 参数估计

本文采用SPSS软件对采集得到的1 358个有效数据进行多项logistic回归分析。如表1所示，将拟定的5个乘客选择候车子区影响因素(X1、X2、X3、X4、X5)作为自变量，将乘客候车子区选择结果作为因变量，通过自变量的似然比检验，以0.050作为显著性水平，可知这5个影响因素对乘客选择候车子区均具有显著的影响效果。

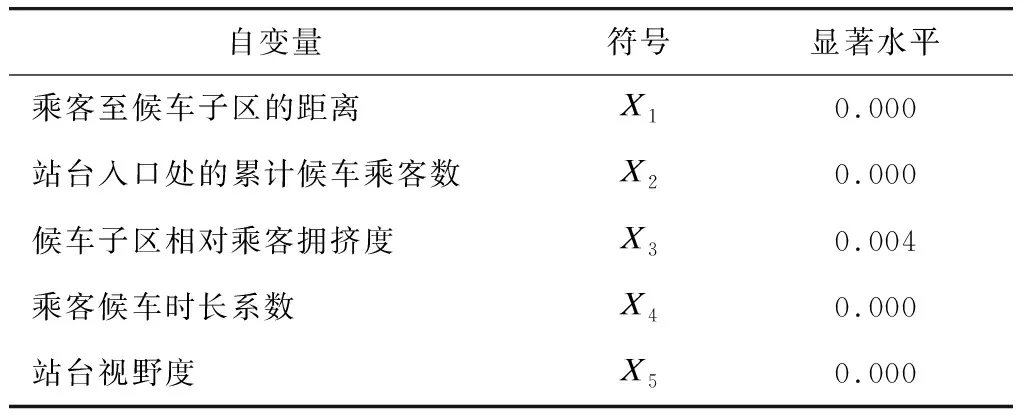
表1 自变量参数表

以最后1个因变量类别(即乘客选择候车子区6)作为参照类，进行回归参数估计。根据式(7)，拟合得到候车子区1～5的站台乘客选择Logit模型方程分别为：

V1=109.886-2.570V1-0.388X2-4.775X3-

14.300X4-13.104X5

(8)

V2=181.608-5.396X1-0.463X2+0.078X3-

25.337X4-16.396X5

(9)

V3=192.769-4.595X1-0.559X2-10.424X3-

9.657X4-48.864X5

(10)

V4=167.154-4.540X1-0.278X2-2.566X3-

4.236X4-30.765X5

(11)

V5=165.293-5.294X1-0.208X2+0.311X3-

8.972X4-16.511X5

(12)

4.2 模型检验

采用SPSS软件对该模型进行似然比检验，得到似然比卡方检验的显著性(P值)为0.000，小于0.050，说明模型整体具有统计性、拟合度高；进行伪R方拟合，得到Cox&SnellR方、NagelkerkeR方、McFaddenR方的值均较大，分别为0.901、0.930、0.666，说明模型具有一定的解释力度，拟合度高。

表2为各候车子区的预测结果精度，采用SPSS软件得到各候车子区内候车客流的预测值及其百分比校正值。选取各候车子区百分比校正的均值(75.5%)作为该模型的总体预测准确率，说明该模型总体上能够较好地拟合候车乘客在各候车子区的分布情况，但在各候车子区的拟合结果准确率上存在一定的差异。

4.3 影响因素分析与优化建议

通过上述研究成果可知：

1) 在七宝站的早高峰时段，站台视野度的系数绝对值普遍较大，因此站台视野度对候车子区选择的影响程度最大，即站台候车乘客会优先选择在自己视线范围内视野度较好的区域进行候车。

2) 乘客至候车子区的距离与候车子区选择显著负相关，说明站台候车乘客更愿意选择距离近的候车子区。

表2 预测结果精度

3) 候车子区相对乘客拥挤度对不同的候车子区呈现出不同的相关性，即当站台各候车子区的拥挤度都较大时，乘客对候车子区相对拥挤度的敏感性降低，乘客则更愿意选择视野度和距离都较优的候车子区2和候车子区5。

4) 乘客候车时长系数对候车子区2和候车子区5的影响程度较大，说明随着候车时间的增加，乘客候车时长系数减小，站台候车乘客会更倾向于选择候车子区2和候车子区5。

5) 站台入口处累计候车乘客数的相对大小会造成候车子区选择的差异性，即当楼扶梯A处的累计候车乘客数较大时，A处的累计候车乘客数对附近候车子区的影响程度大于楼扶梯B处。

为了进一步改善站台候车乘客的不均衡性，根据上述分析结论，本文提出以下建议：①在站台楼扶梯临近候车子区的地板上设置禁停标线，以保留乘客走行空间、改善站台视野度；②当下1班列车还有较长时间才能到站时，及时将客流引导至距离站台楼扶梯较远的区域进行候车；③将客流引导的重心从站台转移至站厅，在站厅增设客流诱导电子装置，根据现场实际客流分布情况将乘客引流至拥挤度较小候车子区附近的站台楼扶梯处。

5 结语

本文将乘客至候车子区的距离、站台入口处的累计候车乘客数、候车子区相对乘客拥挤度、乘客候车时长系数、站台视野度作为影响乘客选择候车区域的自变量，在实测数据基础上利用Logit模型建立了地铁站台的乘客候车子区分布模型。实例分析表明，该模型能够较准确地拟合站台候车乘客的分布情况。在未来研究中，可针对不同站台设施的布局类型分类建立或完善该模型，并引入元胞自动机模型对站台候车乘客的分布情况进行仿真模拟。