HHT在提取Lamb波特征参数中的应用

张 燕

(南京航空航天大学 金城学院，南京 211156)

0 引 言

兰姆波Lamb是一种典型的超声波，它可以在均匀的平板结构内远距离的传播，并且能够敏感感知平板结构细微的损伤。当Lamb波在传播中碰到结构损伤，传播特性会明显发生改变。因此，超声波被广泛应用于板状材料结构的损伤检测[1]。比如在航空飞行器的结构健康检测中，常采用Lamb波对机身机翼等大面积材料结构进行快速检测和数据提取，它的特点是可以对监控数据进行实时提取，快速分析得出结论。传统的Lamb波信息提取方法是Cross-borehole法，方法在很多工业技术工程上都取得不错的效果，但是其缺点是所需传感器数量多，排布密集[2]。在大面积的结构损伤检测中，还有待进一步优化。

近年来，许多信号时频分析方法被研究并用于处理Lamb波信号。其中应用最普遍也较为成功的方法就是希尔伯特-黄变换，简称HHT。算法是美国学者Norden E. Huang在1998年提出的一种新的时频域信号分析方法，它的内容包括：任意一种信号都可以经过经验模式分解法(EMD)分解成固有模态函数(IMF)，然后再对IMF函数进行Hilbert变换得到Hilbert谱[3]。方法最早应用在海洋检测工程中，对非线性数据进行HHT谱分析得到了良好的效果，随后在土木工程结构损伤监测、地震信号分析等领域也验证了其效果。利用HHT对平板结构中Lamb波数据进行分析和处理，获取损伤检测中的时间延迟、能量损耗等特征，并且有效地避免了Lamb的反射和散射所带来的信号混叠。同时进行了实验验证和数据分析，证实了HHT在Lamb信号处理中的有效性和可实用性。

1 HHT算法实现

1.1 兰姆波特性介绍

在结构损伤检测中通常采用窄带脉冲信号作为激励信号，以便于得到信号能量集中而且成分简单的超声Lamb波[4]。产生窄带脉冲信号经常采用Hanning加窗函数，加窗函数具有带宽窄，能量集中的特点，能够明显体现结构损伤的特征[4]，其表达式如下：

(1)

其中，A是信号幅值，H(t)是Heaviside阶跃函数，fc是中心频率采用典型值125 kHz，n是波峰数，该值的选取是降低信号处理复杂程度的关键，为了减少信号混叠，在项目中n=5。

1.2 经验模式分解过程

HHT方法可分为经验模态分解(EMD)和Hilbert变换两个步骤[5]。

EMD分解的核心理念是利用时间序列上、下包络的平均值来确定原始信号的“瞬时平衡位置”，再进一步提取出固有模态函数(IMF)。IMF分量是一种数据序列，需要同时满足两个条件：所有极大值点形成的包络线和所有极小值点形成的包络线的平均值为零，这样可以避免瞬时频率受到非对称波形的影响；整个数据范围内，极值点和零交叉点的数量需要相等，最多相差一个。

根据文献[6-9]，EMD分解步骤具体解析如下：

① 根据3次样条函数对局部极大值点和极小值点进行拟合分别得到和下包络线。

② 计算上包络线fmax(t)及下包络线fmin(t)的均值m(t)=[fmax(t)+fmin(t)]/2。

③ 通过做减法，得到第一个组件h(t)=f(t)-m(t)；如果h(t)不满足固有模态函数的两个条件，就把h(t)当成原始信号，再重复步骤①-③，直到满足条件为止，定义一个IMF ：I1(t)=h(t)。剩余量r(t)=f(t)-I1(t)仍然包含具有更长周期组件的信息，因此把它看作一个新的信号，重复上述过程，可以获得I2(t)，I3(t)，…，当r(t)满足了单调序列或常值序列条件，则停止筛选，认定已完成提取内在模函数的任务，最后的r(t)作为余项，它是原始信号的趋势项。

根据以上步骤可将原始信号f(t) 分解成n个IMF分量及1个趋势项，详见式(2)：

(2)

EMD分解会直接影响HHT方法的分析效果，而在采用EMD分解方法时面临的难题是，由于信号两端不可能同时处于极大值和极小值，所以“筛”过程中构成上、下包络的3次样条函数在数据序列的两端会有发散现象。再者，Hilbert变换过程中，信号的两端也会出现强烈的端点效应。因此，为了确保包络线抵达端点，需要对信号左右两端的极大值和极小值向外延拓[10]。

在实际应用中，几乎没有严格满足IMF两个筛选条件的信号，或者要花费很长的筛选时间，因此可以采用标准偏差SD作为结束筛选的条件，SD的定义见式(3)：

(3)

式(3)中h1(k-1)(t)和h1k(t)代表两个连续筛选的结果。SD的典型值是0.2～0.3，也可以根据实际情况进行调整，获取稳定性良好的线性的IMF分量。此外，可以通过控制筛选次数来保证程序的执行时间及有效性。

1.3 Hilbert谱

按照式(4)，将任一IMF分量Ij(t)进行Hilbert变换：

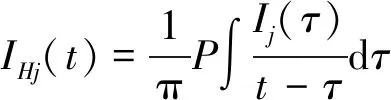
(4)

式(4)中，P是Cauchy主值。

根据式(5)构造解析信号Zj(t)：

Zj(t)=Ij(t)+iIHj(t)=aj(t)eiθ(t)

(5)

式(5)中，aj(t)代表解析信号的瞬时幅值，θj(t)代表相位。

IMF分量的瞬时频率由式(6)表示：

(6)

在同一时频空间内，表示各IMF分量的瞬时幅值与时间和瞬时频率的对应关系，就得到信号的Hilbert谱H(ω，t)，该频谱能够全面反映信号能量在时频域的分布[11]。另外，由式(7)和式(8)可以获取边际谱h(ω)，它反映了信号中不同频率分量能量的大小，还可以获取瞬时能量水平EI(t)，它反映了信号不同时刻能量的变化：

(7)

(8)

实现HHT的流程图如图1所示。

图1 经验模式分解及Hilbert变换流程图Fig. 1 Flowchart of empirical mode decomposition and Hilbert transform

2 实验验证

在结构损伤检测实验中采用复合材料层合板作为Lamb传播介质，其结构常会产生诸如脱层、孔洞以及裂纹等损伤，结构界面会在损伤部位发生变化，从而导致Lamb波在传播中发生能量变化、反射波等。

对Lamb波信号进行HHT分析，得到Hilbert谱、瞬时能量密度谱和边际谱，根据这些数据获取原始信号的特征参数组：Lamb波传播速度、瞬时能量密度谱能量峰值、能量峰值所在时刻、边际谱中心频率及对应峰值等。在结构损伤检测实验中，可以根据实际需要合理选择这些参数。如图2显示了在无损伤平板结构和有损伤平板结构中的Lamb信号经过HHT处理，获取瞬时能量密度水平，从图3中可以发现：损伤信号的能量峰值相比无损信号有了明显衰减，图3边际谱，到达峰值的时间也出现些许延迟。这些关键信息都是结构损伤检测中的判断依据。

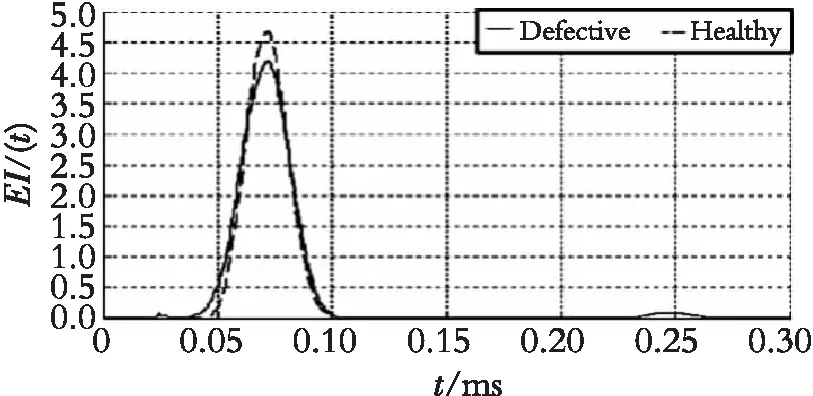
图2 瞬时能量密度水平Fig.2 Instantaneous energy density level

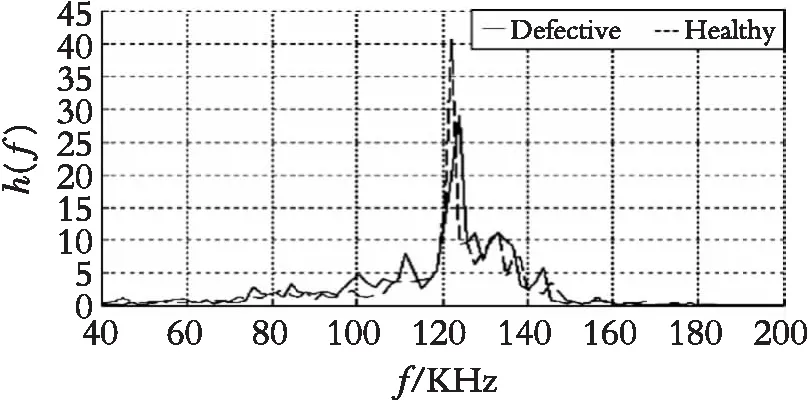
图3 HHT边际谱Fig.3 Marginal spectrum of HHT

3 结 论

对超声Lamb波信号进行了HHT分析，详细介绍了希尔伯特-黄变换的建模方法和步骤，其经验模式分解方法可以有效滤除干扰信号的IMF分量，获取信号的能量和时间信息。复合材料板损伤实验证明了HHT方法具有良好的时频分辨率，尤其是瞬时能量密度和边际谱可以准确有效地提取信号的能量衰减信息和时间延迟信息，对于结构疲劳、微型损伤的早期在线检测提供了可行的方法。