基于到达时间差的曲线交叉点测向算法研究*
2021-07-21刘青琨孙广慧崔逊学
刘青琨, 孙广慧, 崔逊学
(安徽理工大学 电气与信息工程学院,安徽 淮南 232001)
0 引 言
信号源目标定位通过利用一些已知位置的基站或传感器以及测得的信号特征值来求解目标所在的位置。信号源目标定位通过测量信号到达基站或传感器的到达时间(Time of Arrival, TOA)、到达时间差(Time Difference of Arrival, TDOA)、入射角(Angle of Arrival, AOA )等参数,再根据相关的定位算法来估计目标的位置[1]。在各种定位技术中,TDOA技术有着较好的定位性能,得到了研究人员的重视[2]。
基于到达时间差的TDOA测量方程中曲线交叉点参量的计算[3]是两个非线性方程求解未知变量的重要问题。文献[4]中,作者提出了一种思想,对于TDOA双曲线解析方程,从笛卡尔坐标系变换到极坐标系,并通过极向旋转的方法计算出两条双曲线交叉点的位置参量;文献[5]假定已知三维空间中信源的高度,使得目标位置限定在双曲线上,且将TDOA双曲线简化为一条相切的直线,由此确定两条相切直线的交点,作为TDOA双曲线交叉点的近似位置。这些方法虽然在一定程度上可以对交叉点进行求解,但是计算的过程较为繁琐,计算量也比较大,对交叉点的估计精度不高。计算出TDOA曲线交叉点参量后,接着就要研究如何确定权值与组合。文献[6]提出每3个传感器构成一组,根据各传感器至目标的高度差以及测量的TDOA,先估计出目标的二维坐标,然后计算各组传感器与初步估计的目标坐标构成的几何位置关系形成的CRLB,以此作为权重计算出目标位置。但是这些方法并不能合理的确定交叉点的权值,因此,对目标位置的估计并不理想。
针对传统的基于到达时间差的曲线交叉点测向精度不高、权值确定困难的问题,提出一种采用旋转坐标系求出交叉点,根据几何精度因子GDOP来加权不同交叉点参量的方法。从而改善了TDOA曲线交叉点计算过程繁琐,对交叉点的估计精度不高的问题。采用GDOP指标对各交叉点参量取权重综合,很大程度提高了对目标位置的定位精度。
1 到达时间差原理
图1为TDOA的测向原理图,设定位系统共有N号传感器参与定位,其坐标为si=[xi,yi,zi]T,接收到的信号传播时间为ti。将距离信号源近的设为参考传感器,同时将它的位置设为坐标原点,即s0=[x0,y0,z0]T。在以参考传感器为原点,半径为30 m的圆内放置其他的传感器[7]。
设s为去除参考传感器后,其他传感器组成的矩阵s=[s1,s2,…,sN-1]T,到达时间差向量τ=[τ1,τ2,…,τN-1]T,其中τi=ti-t0。信号源真实的位置坐标γ=[φ,θ]T,φ为信号源的方位角,θ为信号源的俯仰角。
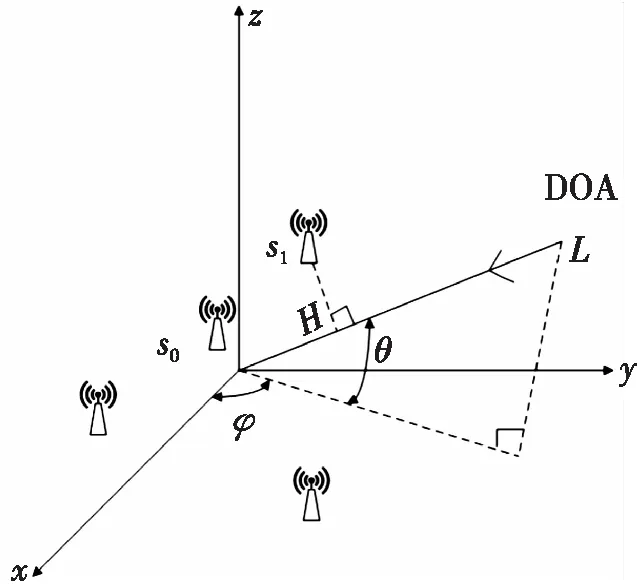
图1 传感器测向原理图Fig. 1 Schematic diagram of sensor direction finding
L为信号传播方向的一点,到基准传感器s0的距离约为1 km。传感器si向s0L作垂线,交点为H。则有s0H长度cτi等于si在s0L上的投影,c为波速。即有如下的TDOA关系:
cτi=sik
其中k为信号的方向[8]矢量。
写成矩阵方程形式:
假定n=[n1,n2,…,nN-1]T为TDOA测量噪声矢量,有

TDOA的协方差矩阵如下:
运用最小二乘法来进行计算,则目标函数可表示为
根据最小二乘原理,W=Cov-1(n)为协方差矩阵求逆[9],获得以下的结果:
2 交叉点算法原理
2.1 TDOA曲线交叉点算法
假设TDOA测量基准传感点位于坐标轴原点,第i,j号传感点是不属于基准的其他两个传感点,其位置分别为si=[xi,yi,zi]T和sj=[xj,yj,zj]T。旋转坐标轴的方法如图2所示。
(1) 旋转过程中坐标原点o保持不动,原x轴旋转后形成的x′轴,指向并通过坐标si。
(2) 在以o,si,sj等3点构成的平面上,在垂直于x′轴的直线上过o点,按右手系确定y′轴的正向。
(3) 在x′oy′平面过o点的垂直线上,按右手系确定z′轴。

图2 坐标轴旋转示意图Fig. 2 Diagram of coordinate axis rotation
根据所设计的坐标轴旋转方式,可确定出坐标变换矩阵Φ,其中Φ矩阵的各列分别是3个旋转后坐标轴的方向余弦。
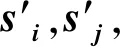
(1)

k=Φk′
(2)
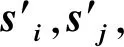
(3)
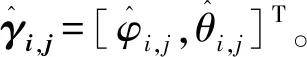
算法两条TDOA测量方程曲线的交叉点的算法
输入:si,sj,τi,τj,c;
设置零点近似范围的微小正数ζ;
fori=1 :N-1
forj=i+1 :N
计算法线向量ax,ay,az,Φ(:,1),Φ(:,3),Φ(:,2);
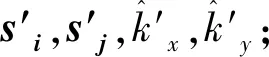
无解
else


end
end
end

2.2 GDOP加权测向算法
假设共有N+1个传感器,令第N+1号传感器为TDOA的测量基准传感器,并位于坐标系原点,并假定第i,j,N+1号传感器与信号源构成的几何结构对应的精度因子为GDOPi,j,令向量g为[g]l=1/GDOPi,j,其中i=1,…,N-1;j=i+1,…,N;l=1,…,N(N-1)/2。将归一化后的GDOPi,j;加权向量记作ρ,则[ρ]l=[g]l/‖g‖1,l=1,…,N(N-1)/2。
(4)
3 仿真实验
3.1 参数设置
均方根误差(RMSE)显示了计算得到的估计位置结果与真实位置结果之间的偏差[10]。克拉美罗下界[11](CRLB)是衡量一种定位算法的性能的指标。将求出的均方根误差与CRLB进行比较[12],以此来判断定位算法的性能。
对仿真实验进行参数设置:使用Matlab进行模拟实验,蒙特卡洛实验为50 000次。实验采用6个传感器进行测向,传感器在半径为30 m的圆形区域内,传感器z轴的坐标在[-5,+5]的区间内。TDOA测量误差服从高斯分布[13],标准偏差在0~25 ms之间。系统误差服从高斯分布,标准偏差在0~15 m之间。
3.2 实验结果分析
模拟实验结果图形中图例的含义分别是:LLS为线性最小二乘法、TS为泰勒级数展开法、EWI法为均等加权的交叉点估计结果、BGI法为最大权重对应的交叉点估计结果、WI法为根据GDOP确定的综合权重对应的交叉点估计结果。
如图3所示,随着信号噪声的增加,所有算法的方位角均方根误差都在不断地增加。LLS和TS的均方根误差较大,在EWI法、BGI法和WI法中,WI法的均方根误差要低于EWI法和BGI法,并且WI法最接近CRLB。
如图4所示,在信号噪声较小时,所有算法的俯仰角均方根误差都比较接近。在信号噪声较大时,LLS和TS的均方根误差都比较大,EWI法、BGI法和WI法的均方根误差十分的接近,但WI法要低于其他两种算法。
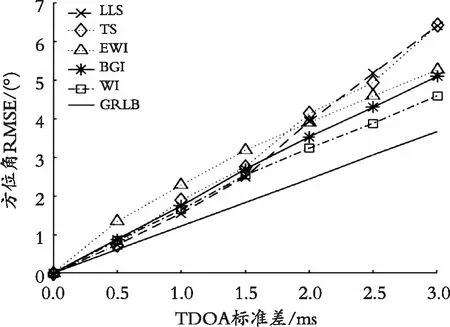
图3 方位角RMSEFig. 3 Azimuth RMSE

图4 俯仰角RMSEFig. 4 Elevation RMSE
实验结果得出,根据GDOP确定的综合权重对应的交叉点估计结果WI法要比均等加权的EWI法和取最大权重对应的BGI法有着更小的定位误差,算法的定位性能要优于其他的方法。因此采用综合加权估计的WI法更能接近克拉美罗下界,提高了对交叉点估计的精度,具有较高的定位性能。所以,选择WI法作为最终的交叉点估计结果。
4 结束语
研究了两条TDOA曲线交叉点的坐标参量计算,这是由两个非线性方程求解两个未知变量的典型难题。针对这一问题,通过坐标系旋转,获得两个非线性方程关于两个未知变量的解析解,即方位角和俯仰角,改善了曲线交叉点测向精度不高的问题;与传统的加权方法相比,采用GDOP指标综合加权估计的WI法对目标位置的估计更加准确,有着更好的定位性能。由于参与定位传感器之间的几何排布结构会产生定位误差,下一步研究将改变传感器的数量和改进传感器的几何排布结构来获得更高的定位性能。
