基于神经网络的基坑紧邻环境多因素预测
2021-07-21仲志煜李建春王月峰
仲志煜,李建春,,张 琦,王月峰
(1.东南大学 苏州联合研究生院, 江苏 苏州 215123;2.东南大学 土木工程学院, 江苏 南京 211189)
随着城市化进程的不断推进,高层建筑的发展伴随着深基坑工程日益增多,其不断增加的深度与规模都对周边紧邻环境形成了巨大的挑战。深基坑工程本身具有空间效应[1]、区域性和独特性。其安全事故往往呈现突发性、随机性的特征。仅凭工程师的工程经验及现场的实时监测难以识别所有的安全隐患,因此有效的预测手段是目前学者及工程师们的研究重点。
传统的预测方法主要有针对平稳序列的自回归模型、灰色理论模型等。自回归模型应用广泛,适用于基坑监测数据的短期预测[2]。灰色系统理论和改进后的无偏灰色模型也多次被应用于深基坑工程预警中[3]。但基坑的破坏往往是受到突发事件的影响,这种突发性的因素导致传统预测模型陷入窘境。而基于神经网络等的机器学习算法,有着计算机的自动建模、实时更新、持续拓展的优势。
目前应用于基坑研究中的神经网络种类丰富,有BP(Back-propagation)神经网络、循环神经网络、径向基神经网络等,也有根据不同条件加入相应算法,或与其他预测方法相结合,提出改进后的融合神经网络。例如,钟国强等[4]在广义回归神经网络的基础上加入混合蛙跳算法,优化了网络的平滑因子,成功对基坑周边地表沉降进行了预测。万荣辉等[5]基于脊波神经网络,使用粗糙集理论算法来对网络中的参数进行优化,完成了对基坑开挖过程中土体变形的预测研究。夏磊凯等[6]将灰色模型与神经网络结合,预测了短期基坑沉降。但在对基坑预测的研究中,多数是认为某一环境只与该点的历史数据有关,很少考虑多个监测点位数据之间的相互影响。国内从20世纪末开始关注深基坑开挖对邻近环境的影响,认为基坑工程不仅需要控制基坑本身安全性和地表沉降,还要关注地下管线、隧道等周边环境的变形控制[7-8]。
笔者拟结合小波分析的降低噪声功能和多元长短时记忆神经网络(LSTM)在长时空分析上的优点,提出WA-LSTM(Wavelet Analysis-long Short-term Memory)预测模型,依托上海徐家汇中心深基坑工程,以地铁结构变形、地表沉降、地下水位变化、支护变形、支撑内力、墙体测斜、管道变形、土体测斜等监测数据为输入数据集,探讨WA-LSTM模型对深基坑工程中紧邻环境时序数据的预测性能,利用多特征LSTM模型将多条序列无缝建模以实现深基坑多个紧邻环境之间的共同分析。并与单特征LSTM、不含小波降噪的LSTM预测结果进行对比分析,以期对深基坑紧邻环境安全态势分析问题提供新的思路。
1 WA-LSTM模型原理
WA-LSTM建模思路的具体过程如下:首先将深基坑工程各紧邻环境的监测数据归一化为[0,1],用小波分析算法将其分解成低频和高频序列;其次将低频子序列提取,同时进行相关性分析,选择不同的输入组合;对每个输出项进行相空间重构,使用排列熵算法选择重构维数和延迟时间。最终将数据集转换为监督学习问题,划分为训练集和测试集,构造成多元LSTM模型,对设定的输出集进行预测。建模流程如图1所示。
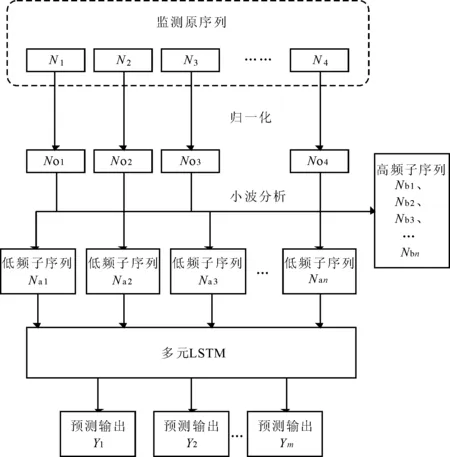
图1 深基坑环境预测WA-LSTM建模流程
1.1 小波分析
小波分析是一种关于时间-频率的分析方法,由Morlet首次提出,是在傅里叶变换的基础上通过一系列运算,对信号(数据)进行不同尺度的分析。近年来,小波分析在各领域科学家的推动下成为了研究热点[9-10]。比利时科学家Daubechies构造的Daubechies Wavelet(dbN)函数是目前最常用的小波分析函数,具有较好的正则性。dbN函数中的N为小波函数消失矩的阶数,N越大,高频子带的小波系数就越小,小波逼近光滑信号的能力越强。本文也采用dbN函数对监测数据进行多尺度分解。因各序列的时频特征相差较大,故采用了不同阶数的dbN函数进行分解。
1.2 LSTM模型
循环神经网络(RNN)将时间长度的概念引入模型,能实现对时间序列数据的建模运算,但RNN存在一些固有问题,无法处理长时数据,同时很容易产生梯度爆炸问题,因此LSTM作为解决短时记忆问题的循环神经网络的一种解决方案,通过增加“遗忘门层”来实现筛选、丢弃、调整信息等功能,近年来被广泛应用于各学科领域,如预测人类行进路径[11]、网约车短时需求量[12]、COVID-19疫情发展趋势[13]等,其网络逻辑架构如图2所示。
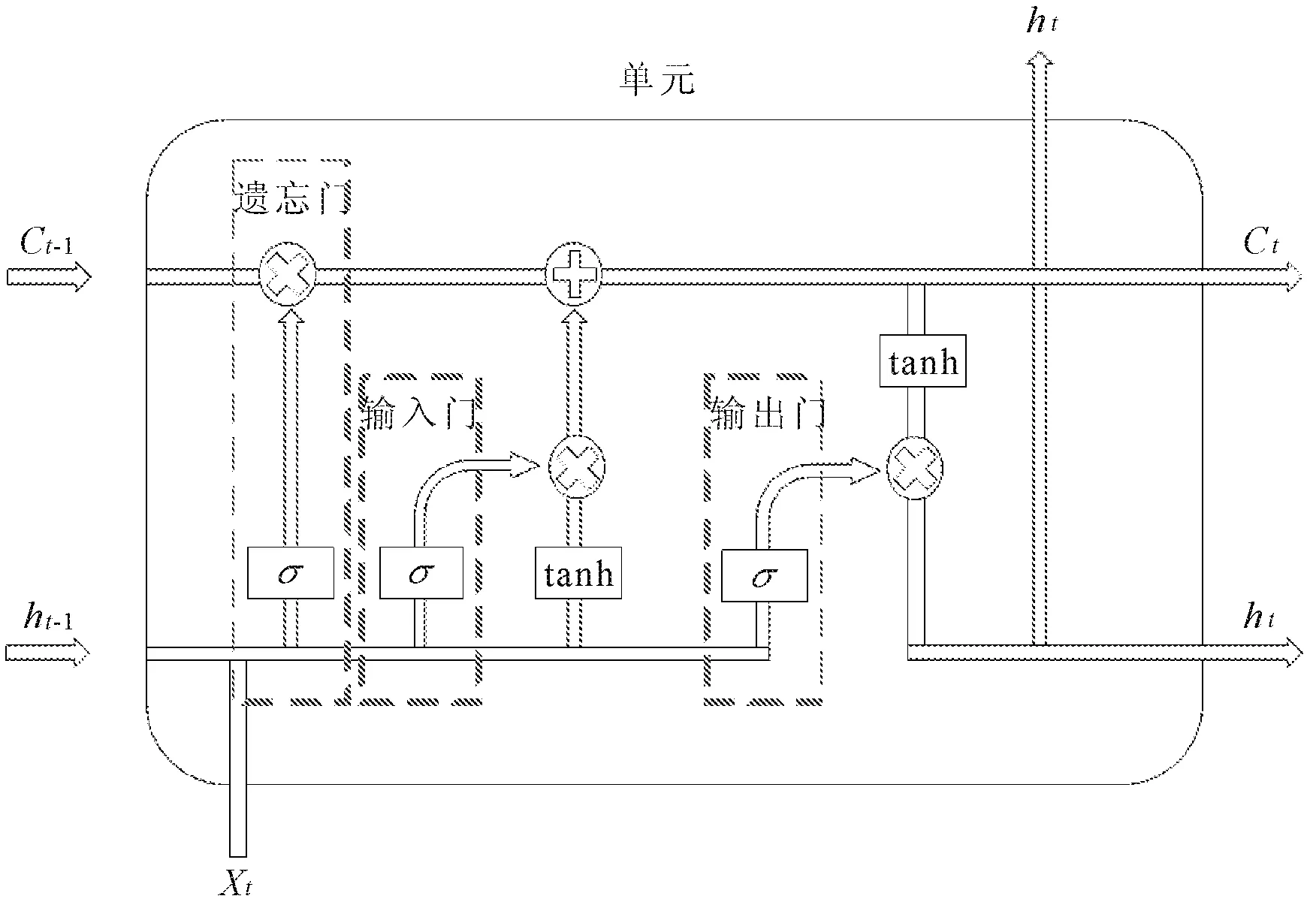
图2 LSTM逻辑架构
LSTM在隐藏神经元开辟的单元中实现传递长时记忆的流程为:单元中输入上一时刻的隐状态ht-1、ct-1和当前时刻的输入Xt,通过式(1)得出期望写入的新记忆流ct、ht。
(1)
式中:σ为激活函数;f(t)为遗忘门,控制信息的记忆与遗忘;i(t)为输入门,控制新记忆的写入;o(t)为输出门,控制期望写入的新记忆输出到下一隐藏层;C(t)为新记忆细胞,tanh为记忆细胞的激活函数。Wf、Wi、Wo、Wc、Uf、Ui、Uo、Uc为单元的权重矩阵。bf、bi、bo、bc为单元的偏置矩阵。
1.3 排列熵算法
排列熵是评估一维时间序列复杂度的一种平均熵参数。它的基本原理是:对时间序列Xi进行相空间重构(重构维数为m,延迟时间为τ),对重构矩阵内的每一行进行数值大小升序排列,得到一组各元素所在列的索引排序,共k组,计算每组索引排序出现的概率为Pj,定义排列熵如式(2)所示:
(2)
Hp值的大小为时间序列的复杂程度,Hp越小,时间序列越规则,可预测性越好;Hp越大,则序列越随机,越不易预测。
2 案例研究
2.1 数据描述
本文数据来源于上海徐家汇中心深基坑工程,该工程位于上海市徐家汇商圈核心地带,总用地面积约66 000 m2,基坑最大深度约33 m。基坑围护采用“地下连续墙+三轴搅拌桩+高压旋喷桩+工法桩”形式,支撑体系采用“钢筋混凝土对撑结合角撑”、“边桁架+钢支撑”形式,支撑立柱采用“型钢格构柱+立柱桩”的形式。基坑紧邻市政管道、高层建筑、道路等对沉降敏感的环境。地铁9号线盾构隧道横穿部分基坑,隧道直径约6.2 m,隧道顶覆土埋深7 m~14 m。
文中选取坑外地下潜水、坑外地表沉降、管道收敛、地铁结构垂直位移、围护墙顶竖向位移、立柱垂直位移、支撑轴力、坑外土体测斜、墙体测斜九类监测数据,分别简写为:SW、DB、9ZXL、9XJ、W、LZ、ZL、XTX、XCX。各环境选取3个测点。以2019年1月7日至2019年11月4日总共305天的监测数据作为实验数据集。
2.2 分析环境
实验操作系统为Windows10,编程语言为Python3.7,算法平台为Keras(基于Tensorflow2.0)。
2.3 性能指标
本文选用均方根误差(RMSE)、平均绝对误差(MAE)和拟合优度(R2)作为实验的性能指标, 如式(3)、式(4)、式(5)所示:
(3)
(4)
(5)
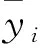
2.4 小波分析
首先对原始数据集Xi{i=1,2,…,n}进行归一化处理,如式(6)所示:
(6)
式中:Zi是归一化后的序列;Xmax和Xmin为该序列中最大值和最小值。
衡量去噪效果可以通过对比不同去噪函数之间的残差标准差、残差绝对偏差两个参数。残差即原序列与去噪后的序列之差,残差越大,被消除的噪声越多,序列就越光滑,丢失信息越多。残差标准差和绝对偏差越小,表示序列之间相似度越高。本文去噪参数均选用固定形式软阈值和无标度白噪声。以地下水位SW33监测序列为例,不同dbN函数的去噪效果如表1所示,去噪后的序列如图3所示。
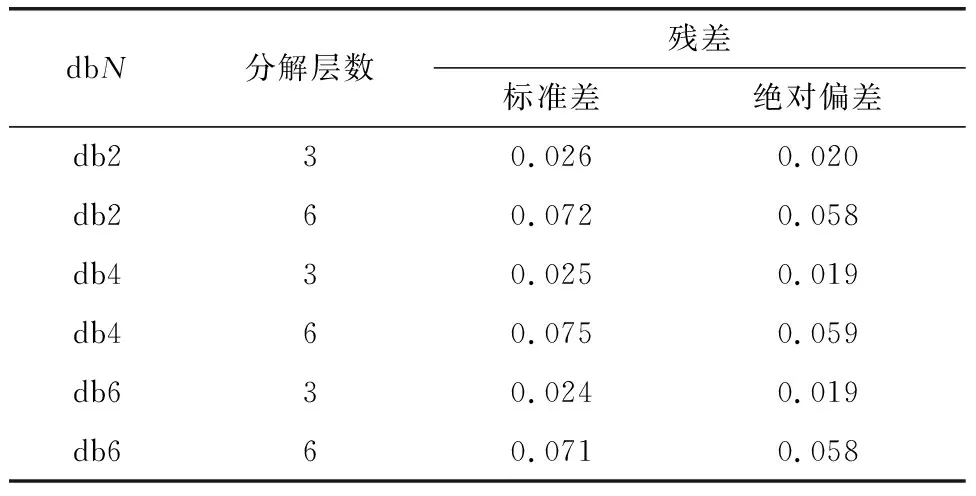
表1 SW33去噪参数对比
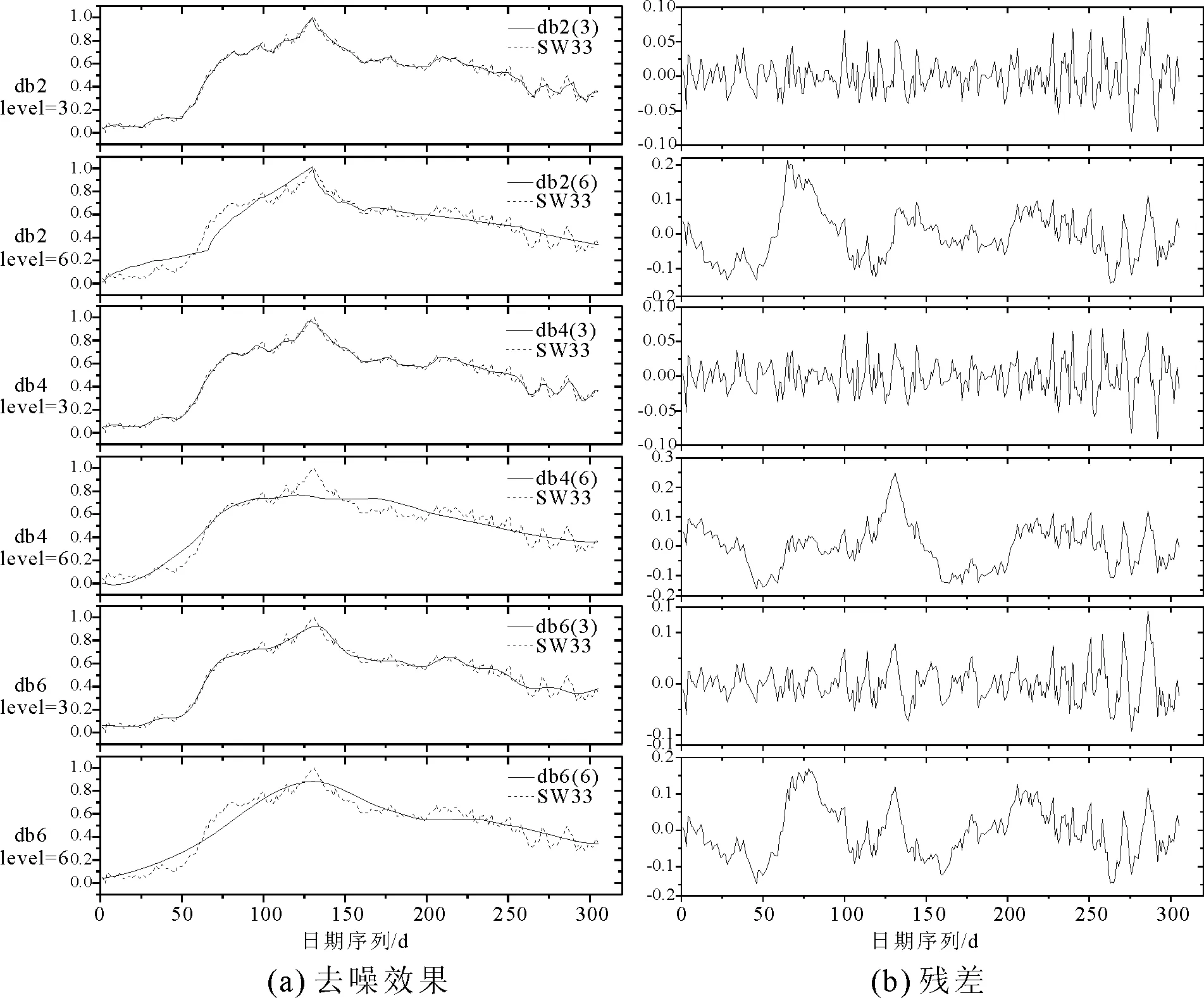
图3 不同dbN函数的去噪效果和残差图
由图3可知,消失矩N对低层数分解的影响较小,而分解层数对去噪效果影响较大,层数越高,去噪后的序列越平滑,但相应的残差呈现较为明显的波动趋势,原序列本身的信息可能被消除。为保留原序列本身的信息,同时进行适当去噪,本次实验均使用db3及db4函数进行分解。
基于数据集不同的噪声大小,不同测点数据采用不同的dbN函数,如表2所示,同时提取坑外地下潜水、坑外地表沉降等九类监测项的低频子序列a3,各取一个测点为例汇总如图4所示。
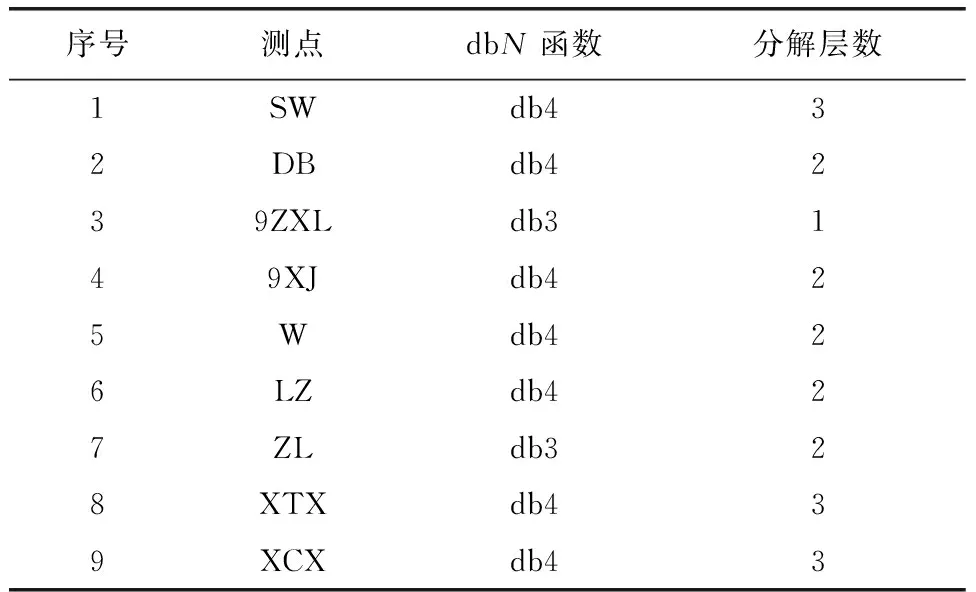
表2 dbN函数及阶层的选用

图4 9项小波低频序列汇总
2.5 相关性分析
深基坑紧邻环境之间的影响关系互不相同,影响力大小受测点空间距离、内在因果关联等因素影响。计算皮尔逊(Person)相关性系数可以衡量两个连续序列随时间共同变化的关联度。以[-1,1]区间衡量相关性强度,-1为完全负相关,0为不相关,1为完全相关。以热力图形式表示相关性大小,-1和1为黑色,0为白色,如图5所示。

图5 各序列相关性大小
皮尔逊分析结果表明,地表沉降、地铁结构位移、围护墙顶竖向位移、立柱垂直位移、坑外土体测斜、墙体测斜之间有很强的相关性。以此结果作为初步筛选依据,选取三类典型环境:地表沉降、地铁结构位移、坑外土体测斜为输出项,制定表3多因素实验方案。

表3 多因素实验方案
2.6 多元LSTM模型构建
Keras在LSTM的参数选择上提供了多种初始化方案,本文采用Glorot均匀分布初始化器,它是根据权值张量中的输入和输出单位的数量构造相应的均匀分布并从中抽取样本。本文采用自适应矩估计算法自动为模型中的每个参数(权重)使用自定义学习率,初始学习率为0.001。同时使用排列熵算法,设定延迟时间为1,重构维数为[1,10]之间,对输出项进行排列熵计算,选取最小熵值的重构维数m作为LSTM输入的预测所用天数,即用前m-1的数据预测下一天的数据。
本文将输入数据集中前259 d数据作为训练集,后43 d数据作为测试集。本次实验分为三组,分别以坑外地表沉降、地铁结构垂直位移、坑外土体测斜为输出项,每组设立单因素、双因素、三因素和多因素不同输入项。并设置LSTM层数为1,时间步长为1,隐藏层维度为100,每个批结束后,重置LSTM的内部状态。
2.7 实验结果分析
本次实验各模型的损失函数表现相近,其中单因素输入、双因素输入、三因素输入模型的MAE值均在遍历20次时已趋于稳定,而多因素输入在600次左右达到平衡。以DB46实验组为例,各模型的损失函数如图6所示。

图6 4组WA-LSTM模型损失函数图
具体预测性能结果可见表4,三组实验均运行良好,MAE在每次遍历时均有波动,但都稳定在较低水平。三组实验中双因素LSTM测试的RMSE值均为最低,R2最接近1,预测误差最小。随着输入项的增加,多变量LSTM的训练时间也随之增加。三组实验的测试结果均能体现:双因素>单因素三因素>多因素(三因素以上)的预测精度。而多于三因素的输入需要更大的批次大小和遍历次数,使得网络泛化性不佳。为更好的对模型进行评估,本文对原始序列、WA-LSTM(双输入)、WA-LSTM(单输入)、不含小波的LSTM模型的预测结果进行对比分析,后43 d的数据结果如图7—图9所示。
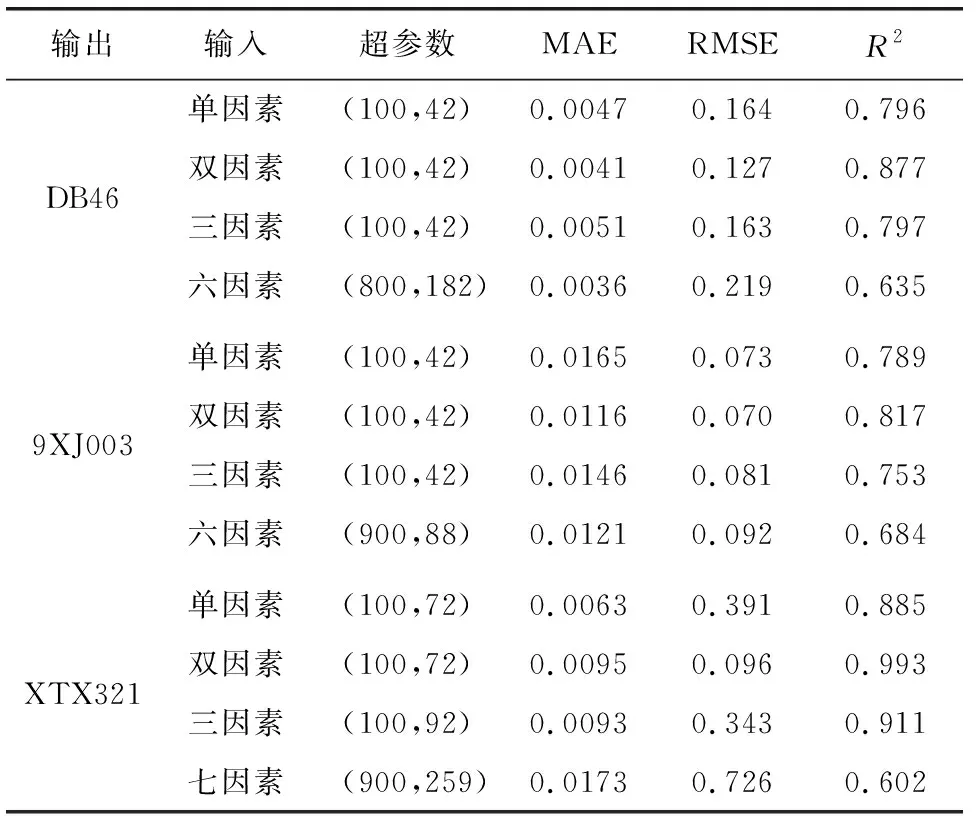
表4 预测性能对比

图7 DB46多种模型预测结果

图8 9XJ050多种模型预测结果

图9 XTX321多种模型预测结果
其中,超参数(e,b),e为遍历次数,b为批次大小。
对比图7、图8与图9,可以发现:坑外地表沉降(DB46)曲线波动性明显,地铁结构垂直位移(9XJ003)在第270天处存在突增现象,坑外土体测斜(XTX321)整体趋势较为平滑,不存在大幅波动或异常变化。
从上述三组不同输出项的预测结果对比中可知,WA-LSTM(双因素)模型在处理存在波动的地表沉降、存在异常增加的地铁结构位移和变化平滑的坑外土体测斜数据时均取得了最好的预测效果,整体变化趋势也更加平滑,但在对部分极值点的预测上,不如单输入和不含小波去噪的模型。小波模块对数据的平滑处理能有效减少噪声影响,其中原始序列预测的极值点比含有小波去噪的模型更接近原数据。
3 讨 论
原始工程监测数据由于在采集过程中会受到环境影响,本身的误差影响较大,且每日采集数据的时间点并不固定,数据的时间间隔并不是严格的等间距,多种因素导致原始数据出现大量极值点。而小波分析工具可以有效减少噪声影响,使数据变化曲线更为平滑。因而在实验过程中,即使WA-LSTM普遍对极值点的预测不如不含小波去噪的预测模型,但对原数据的趋势性上还原程度很高,更符合现场实际。其中双因素模型在变化趋势上更贴近原数据。不少学者也已验证了多元LSTM网络在土体滑坡[14]、工业传感器[15]等领域的可行性。
此外,随着LSTM的输入项增加,网络对超参数敏感度变高,可调参的范围缩小,在多于四个输入项时,预测精度反而有所下降。这是由于多条时间序列之间的影响关系错综复杂,没有很好地对几条序列进行分类。在往后的研究中,可以尝试在WA-LSTM模型中加入权重分析或空间关系分析模块,如卷积神经网络等[16],使多时间序列在空间上的关系更为明确,以降低网络的敏感程度,使预测结果更为精确。
4 结 论
(1) 本文在LSTM模型的基础上加入小波去噪处理模块,使得预测曲线更平滑、准确,更符合工程中的理论变化趋势。在小波函数的选用上,dbN函数能很好的根据噪声大小选用不同的阶层,使得处理后的低频序列能较好地反映原数据整体的变化趋势和细节。
(2) 本文在皮尔逊相关性分析的基础上,在WA-LSTM模型中选用不同组合的深基坑紧邻环境监测数据作为输入项,发现在预测地表沉降时考虑围护墙顶竖向位移、在预测地铁结构位移时考虑坑外土体测斜、在预测坑外土体测斜时考虑围护墙顶竖向位移,其预测结果都比单因素分析更为精确。可见双因素模型较单因素和多因素模型更能包含空间影响,能有效提高模型预测精度,在预测波动、异常增减、平滑等数据中均取得良好效果,为深基坑紧邻环境安全态势预测提供了新的思路。
