基于NSGA-Ⅲ和FloPy的灌区水资源多目标模拟优化模型

康燕楠，降亚楠,2，苏振辉

(1.西北农林科技大学 水利与建筑工程学院， 陕西 杨凌 712100；2.西北农林科技大学 旱区农业水土工程教育部重点实验室， 陕西 杨凌 712100)

我国是农业大国，水资源与农业生产和粮食安全密切相关。在气候变化和人类活动的双重影响下，我国部分灌区出现了水资源短缺和生态环境退化的现象。近年来，位于北方干旱半干旱地区的大型灌区，地表水源难以满足农业发展以及生产生活的需求，地下水成为主要的灌溉水源，据统计大约有70%的地下水用于农业灌溉[1]。由此导致部分灌区的地下水处于超采状态，尤其在干旱缺水年份，来源于降水的天然补给量减少，河流和渠道用水不足时，灌区会大量开采地下水。不合理的地下水开发利用容易导致采补失衡，致使部分区域地下水位持续下降，形成大面积的水位降落漏斗，进而引发了一系列生态环境问题，制约了灌区的可持续发展。因此亟需考虑灌溉效益和合理的地下水位上下限，对灌区内有限的水资源进行合理配置，使其发挥最大效益[2-3]。水资源作为灌区资源和环境的双重要素，对农业生产和生态环境保护起到核心作用，对以地表水和地下水为主的农业水资源进行合理配置是解决灌区缺水问题的重要手段。

灌区水资源合理配置需要综合考虑经济、环境及社会等多方面的目标，是一个典型的多目标问题。针对地表水和地下水联合利用的水资源合理配置，目前国内外的研究趋势是将优化算法和地下水数值模拟模型进行耦合建立模拟优化模型来解决该问题。求解水资源优化配置的算法主要包括粒子群算法[4]、人工鱼群算法[5]、模糊多目标线性规划[6]、遗传算法[7]及鲁棒规划方法[8]等，由于它们能够处理较为复杂的多目标问题，因此在水资源优化配置中得到广泛应用。Davijani等[9]采用遗传算法和粒子群算法两种启发式算法，将水资源合理分配给工业、农业和市政部门。谭倩等[8]采用鲁棒规划方法，对多个目标进行权重分析以便于决策者确定最优方案。

部分研究通过构建耦合地下水数值模拟模型和灌区水资源模拟优化模型来进行灌区水资源优化配置。目前常用的地下水流数值模拟软件主要有MODFLOW、FloPy[10]、GMS[11]、FEFLOW[12]等。Sedki等[13]将地下水非稳定流模拟模型与基于遗传算法构建的优化模型相结合，构建了多目标地下水资源可持续管理模型，在寻找最佳抽水方案的同时最大程度降低了对环境的不利影响。高玉芳等[14]为解决沿海地下水超采所引发的海水入侵问题，将MODFLOW的变密度地下水流及溶质运移模型与人工鱼群算法相耦合，构建了地下水模拟优化管理模型。宋健[15]基于多目标进化算法构建了复杂地下水系统的模拟优化模型，用来解决滨海地下水管理和地下水污染监测网优化问题。为了解决实际应用中多个目标函数(大于3)的高维多目标优化问题，Deb等[16]提出了基于参考点的第3代非支配排序遗传算法(NSGA-Ⅲ)，Blank等[17]基于Python语言开发了一个多目标遗传算法框架Pymoo。金江跃等[18]通过假想案例构建了一个多目标地下水模拟优化模型。当前灌区的水资源优化配置倾向于将优化配置结果代入地下水模拟模型进而评估优化配置方案对地下水的影响，属于单向传输过程，而能够动态双向传输的遗传算法与地下水耦合模型目前多应用于地下水超采造成的海水入侵问题，针对灌区地表水地下水联合优化配置进行紧密耦合的研究较少。因此本文构建了基于NSGA-Ⅲ和FloPy的灌区水资源多目标模拟优化模型，实现了优化算法与模拟模型之间的紧密耦合和动态的数据交换，并通过一个假想算例验证了该模拟优化模型在渠井结合灌区的有效性和可靠性，为灌区水资源优化配置和可持续高效安全利用提供了强有力的技术手段。

1 研究方法

1.1 地下水数值模拟模型MODFLOW与FloPy

MODFLOW是一个采用有限差分法进行地下水流数值模拟的软件，它由一个主程序和若干个相对独立的子程序包构成，每个子程序包又包含数个子模块来分别完成模拟的一部分[19]。例如用井Well包模拟抽水井和注水井对地下水的影响。

FloPy是Bakker等[10]基于Python编程语言开发的可以运行MODFLOW、MT3D、SEAWAT等模型的地下水建模工具，它可以通过Python语言构建和运行地下水数值模拟模型，且便于和优化算法耦合构建地下水模拟优化模型。Python是目前功能强大的软件开发语言之一，可以借助扩展包完成绘图、数据分析和优化等过程，具有脚本语言中最强大的类库和更完整的数据结构集。基于Python语言开发的FloPy具有创建新模型、导入运行已有模型、读取和绘制模拟结果等强大的功能。在Flopy中建立MODFLOW模型通常包含以下八个步骤：(1) 导入FloPy包；(2) 创建MODFLOW模型对象；(3) 设置模型的基本参数离散化、边界条件、水文地质参数和图层类型等；(4) 添加对应的子程序包(例如井Well、补给Recharge、河流River)；(5) 定义MODFLOW水头求解方案；(6) 定义MODFLOW需要保存文件的输出类型；(7) 生成MODFLOW输入文件并调用MODFLOW获得求解方案；(8) 读取输出文件并可视化进行分析。

import flopy

dis=flopy.modflow.ModflowDis(model, nlay, nrow, ncol, top=ztop, botm=botm)

pcg=flopy.modflow.ModflowPcg(mf)

hds=bf.HeadFile(‘Example’+“.hds”)

但对于边界条件和水文地质情况复杂的区域，难以直接采用FloPy构建模型，FloPy提供了功能强大的API接口来导入其他软件构建的MODFLOW模型。如基于GMS构建的模型在选择保存为通用的MODFLOW格式后，即可通过FloPy的fmp.Modflow.load语句导入，model = fpm.Modflow.load(‘Example.mfn’, version=‘mf2005’,verbose=False,check=False)。FloPy可以正确地识别定义模型的离散化、活动单元格、顶底板高程、水力特性和其它源汇项，进而修改和运行模型。FloPy兼容MODFLOW-2000、2005、NWT、USG、LGR和最新版本的MODFLOW6。

FloPy可以通过编程的方式修改所导入模型的渗透系数、井模块、补给模块以及河流模块等，也可以便捷地读取地下水位模拟结果来计算遗传算法中适应度函数的值，进而实现与多目标遗传算法的紧密耦合。

1.2 多目标优化框架Pymoo

Pymoo是为解决多目标优化的问题，基于Python语言开发的遗传算法框架，可以通过模块化和基于对象的编程来实现扩展。主要包括优化问题构建、优化算法实现以及数据分析在内的三个主要的功能模块。Pymoo提供了相关的性能指标来衡量多目标优化算法获得结果的质量并将其可视化输出。

本研究中选用Deb在2014年提出的多目标遗传算法NSGA-Ⅲ，它引入参考点机制，对于那些非支配并且接近参考点的种群个体进行保留，来维持种群的多样性。假设M为目标数目，P为每个方向上分割的份数，其计算公式为H=(M+P-1P)。

目前研究中，NSGA-Ⅲ对求解3-15个目标函数问题有良好的适用性，该算法的基本框架如图1所示。

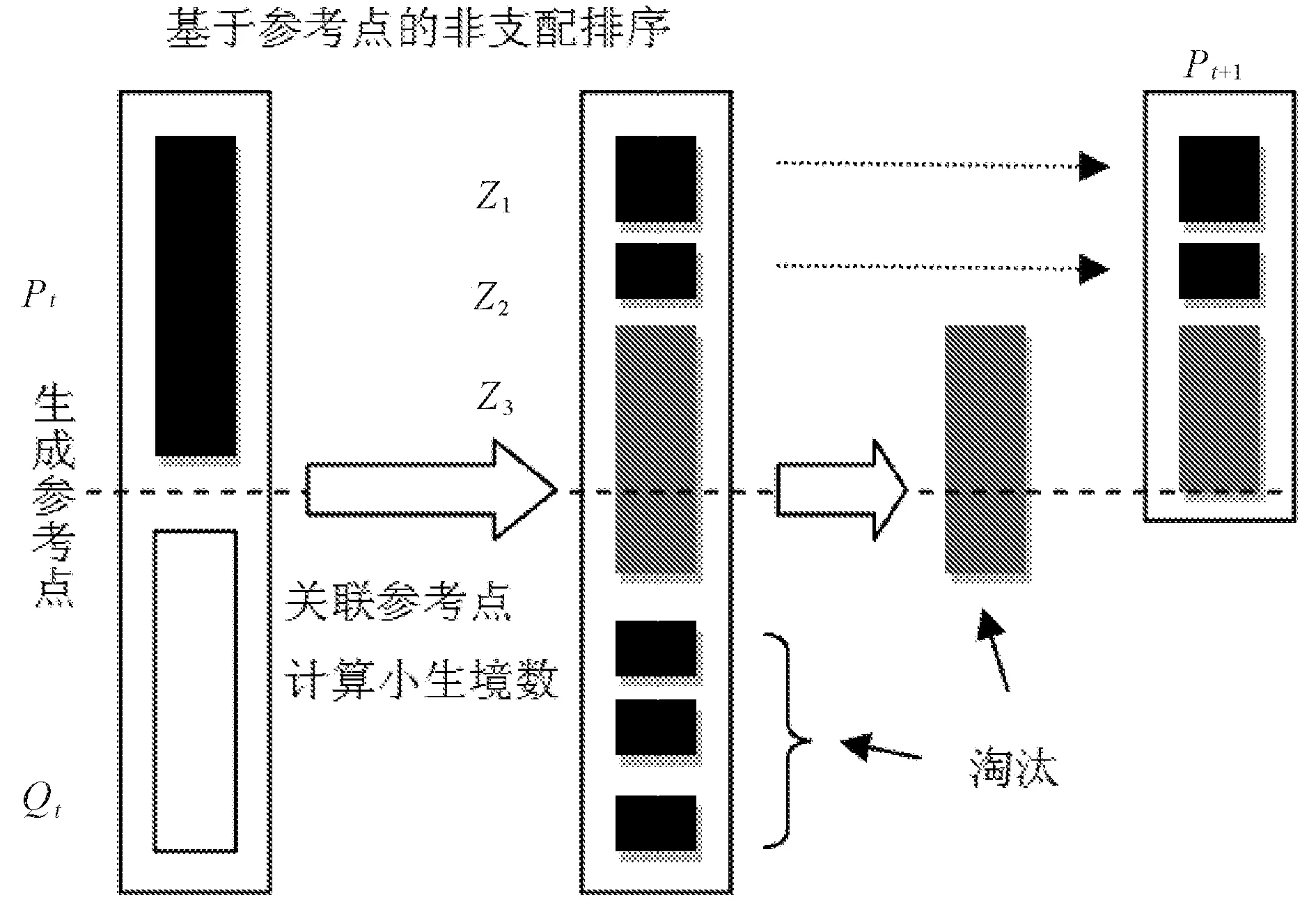
图1 NSGA-Ⅲ的基本框架

1.3 耦合模型的构建

在FloPy与Pymoo耦合时，需要在Pymoo中调用FloPy模拟结果来计算与地下水位和地下水开采费用有关的目标函数值，并读取地下水位来判断开采方案是否可行(地下水位是否在合理范围内)，将FloPy作为能被Pymoo调用的子程序，实现二者之间数据的无缝传输。本研究采用Pymoo框架中的遗传算法NSGA-Ⅲ进行多目标优化模型的求解，其寻优是一个循环过程。当循环开始时，需要根据所设置的种群大小，对决策变量中各参数进行初始化，形成第一代种群。将该种群作为可行解集，其中的每一个体都需要调用一次子程序FloPy进行对应方案下的地下水模拟计算，得到相应的模拟结果。然后Pymoo将根据模拟结果判断该方案是否满足设置的约束条件，并计算目标函数值，对各可行解进行评价，得到新一代的种群。重复上述步骤，直至达到收敛条件，耦合模型的构建流程如图2所示。

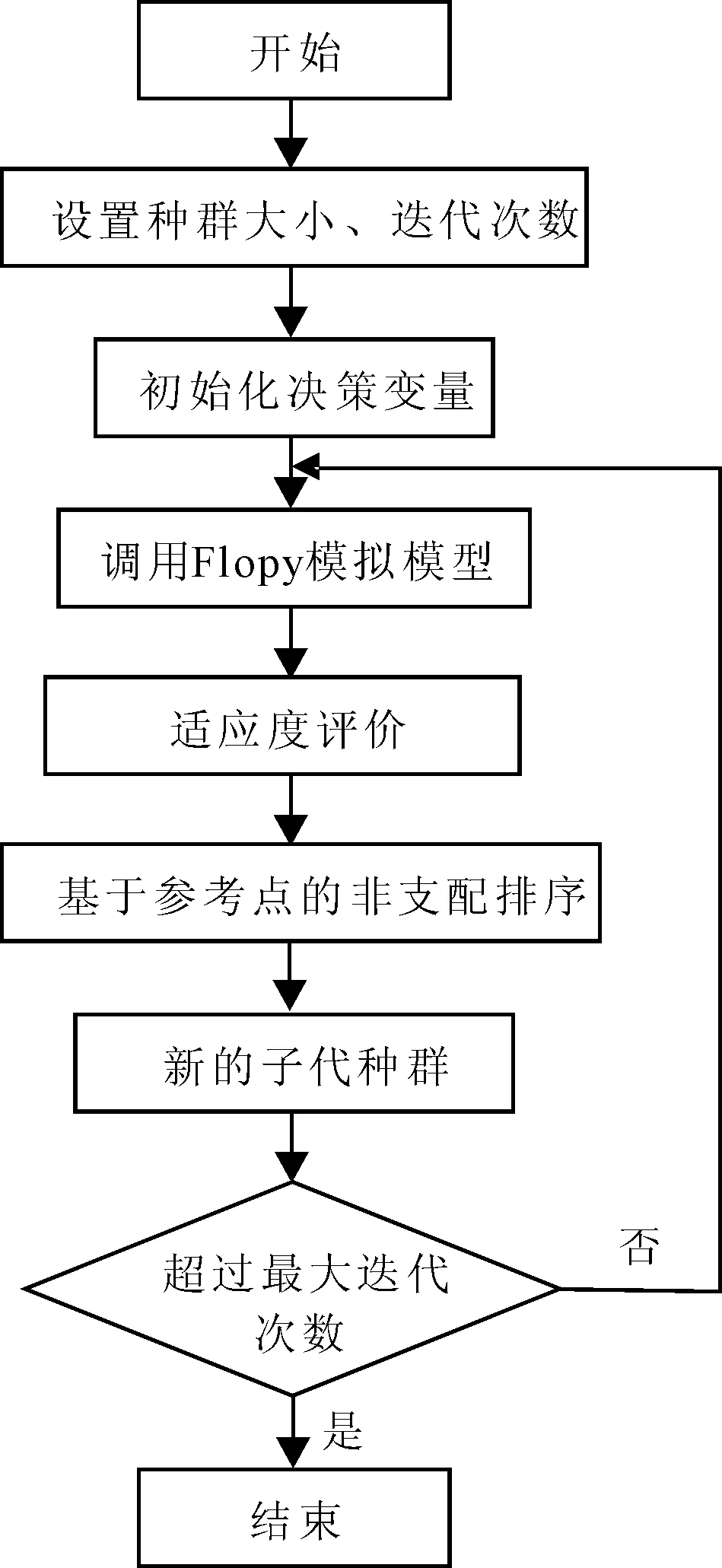
图2 耦合模型构建流程图

2 算例研究

2.1 算例背景

由于实际灌区情况非常复杂，缺乏构建模拟优化模型所需的基础数据(如具体的井位)，因此本文在对西北干旱半干旱地区的典型渠井结合灌区——陕西省宝鸡峡灌区进行调研的基础上，综合考虑灌区实际条件设计了一个包含若干水文地质分区的典型灌域来进行模拟优化模型的构建验证和结果的分析论述。该区域长5 km，宽3.5 km，在MODFLOW模型中将该区域在空间上剖分为50行50列的长方形网格，根据水文地质条件和种植作物的不同分为5个区域。其中分区1、5和2、3、4的地下水埋深不同，来模拟宝鸡峡灌区塬上和塬下两个灌溉系统。假定研究区为非均质各向同性的潜水含水层，地下水流向为从西到东，两边水头差设为5 m。东西边界概化为定水头边界，南北边界概化为零流量边界。灌域内共布置50眼抽水井，其井网密度为3眼/km2，构建的水文地质概念模型如图3所示。

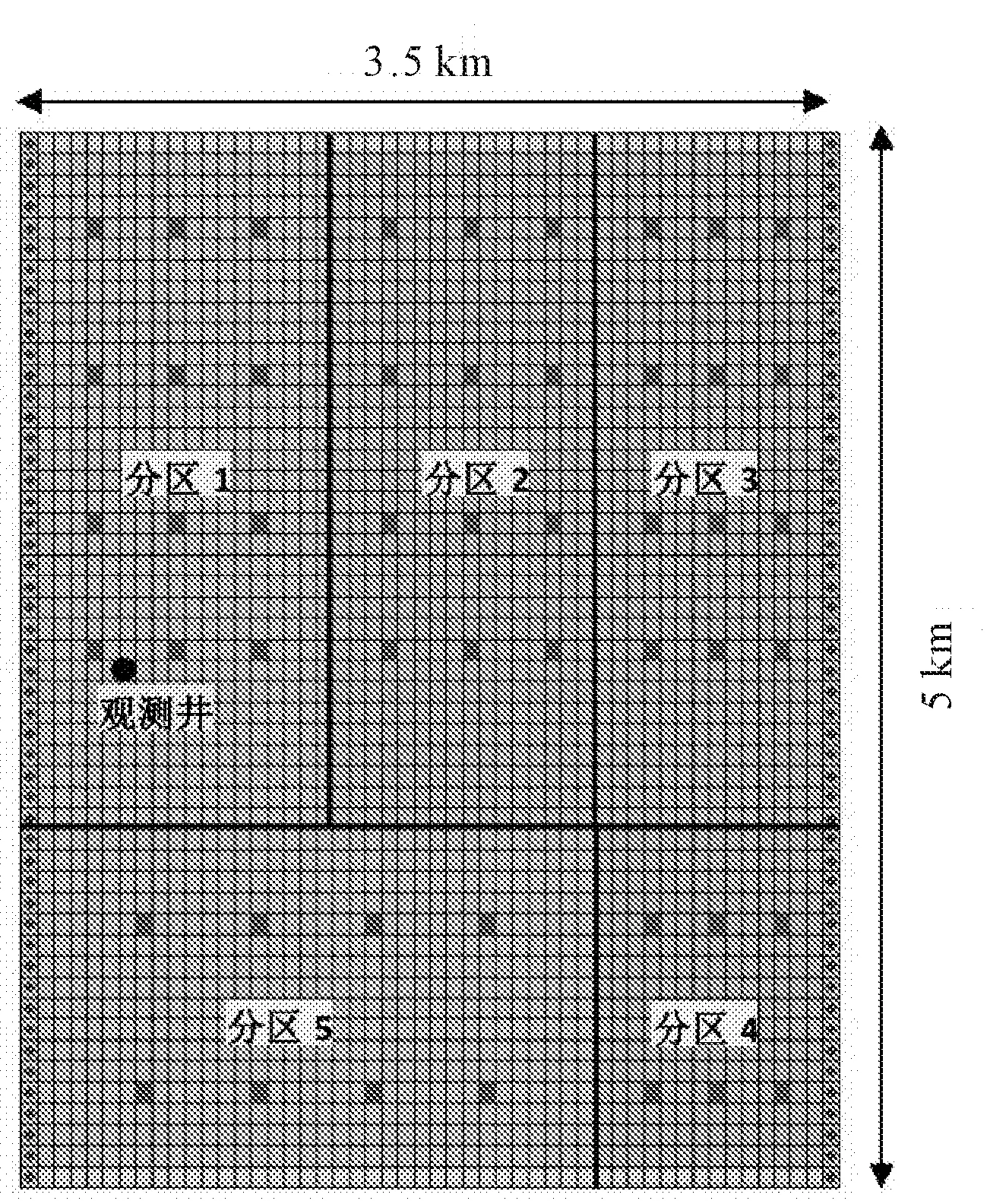
图3 水文地质概念模型

采用2009年灌区某气象站的逐日降水资料进行计算，计算时段为2009年1月1日至2009年12月31日，计算时间步长和应力期均设为1 d，基于GMS构建了地下水非稳定流数值模拟模型。将其保存为原始MODFLOW格式后导入FloPy用来计算不同方案下的地下水位。本研究将降水入渗补给、田间灌溉入渗补给、井灌回归补给按照面状补给形式补给地下水，地下水开采采用MODFLOW中的井模块进行模拟。算例相关的水文地质参数和种植结构及种植面积分别如表1和表2所示。

表1 水文地质参数

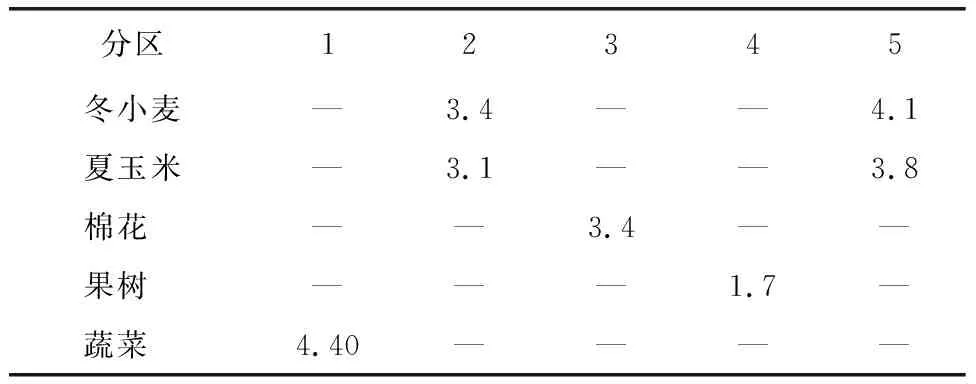
表2 种植结构及种植面积 单位：km2

2.2 决策变量

针对本研究问题，共设置19个决策变量，分别为抽取地下水量Gij以及各作物生长过程的供水比例anj。其中Gij为各分区抽取地下水量，m3；anj为各作物第n次灌水量与N次总灌水量之比；i为分区编号；j为作物类型编号。

(1)

2.3 目标函数的建立

灌区水资源优化模型中目标之间往往存在竞争关系，所以需要考虑不同层次利益主体的目标[16]。因此，本算例设置的优化目标是满足最大抽水降深约束的条件下，实现下层决策主体(农民)的目标：作物总产量最大以及经济效益最大，并同时实现上层决策主体(灌区管理者)的目标：地下水平均累计降深最小。

(1) 产量目标：各分区作物总产量最大

(2)

式中：Z1是每公顷作物总产量，kg；i是分区编号，i=1，2，3，4，5；j是作物类型编号，j=1，2，3，4，5，分别是小麦，玉米，棉花，果树，蔬菜；Qij为不同分区作物的总需水量，m3；Aij为不同分区作物的种植面积，hm2；f是描述产量与生育期耗水量的二次函数关系，通过查阅相关文献确定灌溉量与作物产量之间的具体关系如公式(2)—公式(6)所示[20-24]：

(3)

(4)

(5)

(6)

(7)

式中：f1、f2、f3、f4、f5、Q1、Q2、Q3、Q4、Q5分别为冬小麦、夏玉米、果树、棉花以及蔬菜的产量和全生育期需水量。

(2) 经济目标：农业用水产生的净效益最大

(8)

式中：Pij为各作物的单价，元；Csi为渠道引水的价格，0.27元/m3；Cg1和Cg2分别塬上和塬下抽水灌溉的价格，0.16元/m3和0.11元/m3；Gij为各分区抽取的地下水量，m3。

(3) 地下水平均累计降深目标

该指标表示每日某网格的地下水位相较于前一天该网格地下水位下降值(不考虑前一天地下水位值低于当天水位值的情况)的累计年平均值。

(9)

式中：k是各网格编号，k=1，2，3…2500；t是决策时段长度，t=1，2，3…365，d。

2.4 约束条件

(1) 地下水变幅约束：

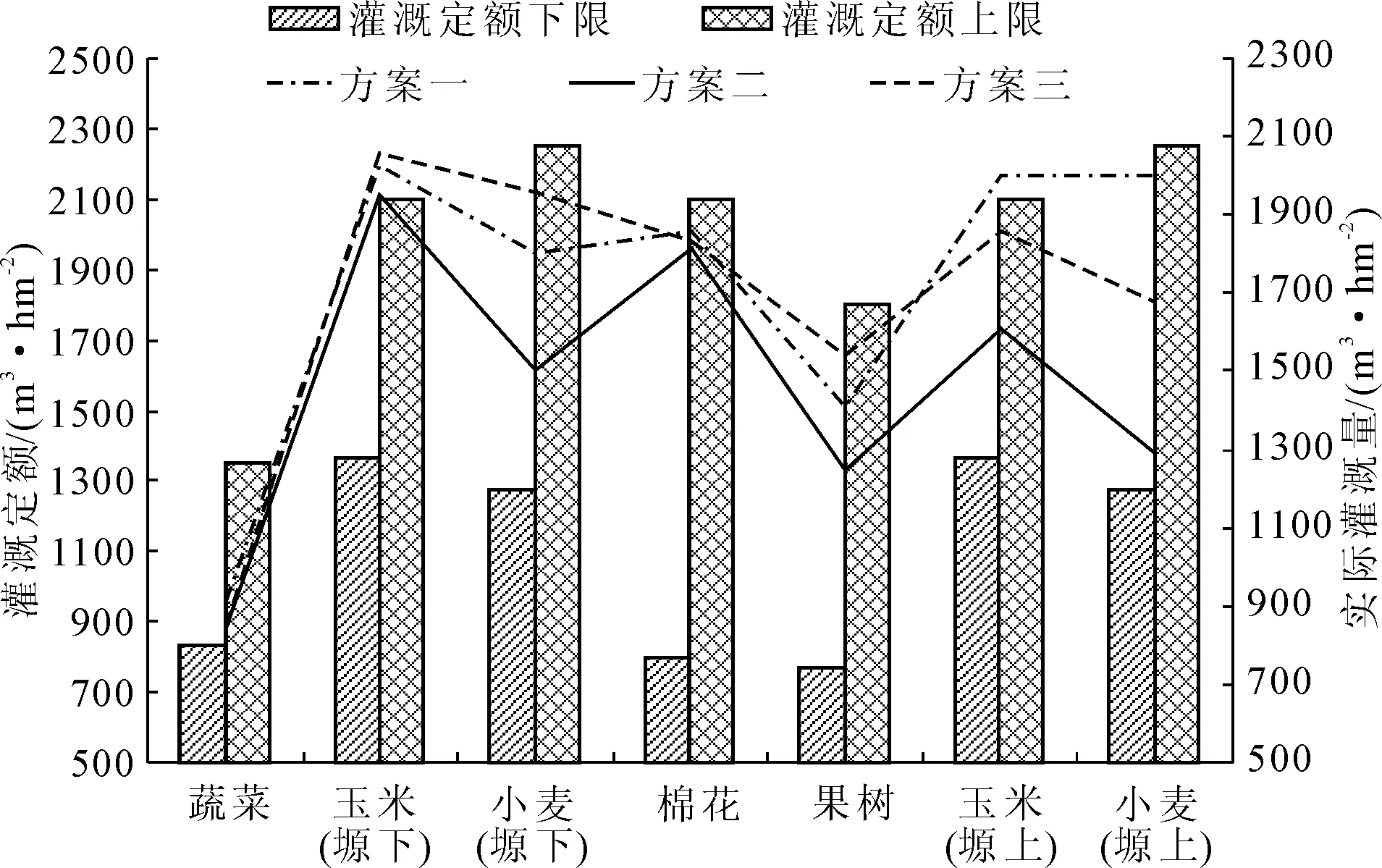
hmin

(10)

式中：hmax为该区域平均合理地下水埋深的上限阈值，m；hmin为该区域平均合理地下水埋深的下限阈值，m。参考地下水配置的相关研究，将塬下地下水埋深的上限阈值设置为2.43 m，下限阈值设置为14.79 m；塬上地下水埋深的上限阈值设置为3.05，下限阈值设置为58.05 m。

(2) 需水约束：

ETmin,ij

(11)

式中：ETmin,ij为各分区不同作物的最小需水量，m3/hm2，本文取灌溉定额的60%；ETmax,ij为各分区不同作物的最大需水量，m3/hm2，本文取灌溉定额。

3 优化结果及分析

3.1 参数设置和求解过程

NSGA-Ⅲ的参数设置：种群大小N=200；优化搜索代数为100；使用二进制交叉和多项式变异，其中交叉率Pc=0.7，变异率Pm=0.05。

多目标优化算法求解结果可用超体积指数(Hypervolume)来评价，其表示由非劣解集中的个体与参考点在目标空间中所围成的超立方体的体积，以评价解集的收敛性与分布性，该指标评价方法与Pareto保持一致，指标越大，表明Pareto前沿的占优性越强。算例的Hypervolume指标见图4，初始种群在第40代左右可达收敛水平，并逐步寻找最优解集。

图4 HV评价指标

3.2 优化方案分析

水资源多目标优化不能得到单一的全局最优解，而是由多个非劣解构成的非劣解集。其中包含倾向于不同目标的多个方案，本文从非劣解集中选择三个典型方案进行对比分析(见表3)，具体结果如图5所示。由表3可以看出，三个典型方案分别侧重于产量最大、地下水平均降深最小和经济效益最大三个目标。

表3 三种方案的目标值

图5 三个水资源配置方案对比分析

优化结果中，方案1作物产量最大的同时地下水平均累计降深最大，经济效益最小，不利于灌区的经济发展；方案2灌区地下水平均累计降深最小，作物产量和经济效益介于方案1与3之间，对地下水的可持续高效安全利用最有利；方案3灌区收益最大，作物产量最小，地下水平均累计降深介于方案1与2之间。大多数研究表明作物产量与经济效益呈正相关关系，但是在本研究中，由于灌区分为两类灌溉系统-塬上和塬下，二者是竞争关系。塬上地下水埋深大，抽水费用高于塬下，导致保证作物产量的同时经济效益较低。因此当考虑经济效益最大时，应优先满足价格最高的果树和抽水费用较低的塬下小麦、玉米的灌水需求；当考虑产量最大时，应优先满足每公顷产量最大的小麦、玉米以及蔬菜的灌水需求；当考虑地下水平均累计降深最小时，应优先满足塬下种植作物的灌水需求，塬上作物仅满足最低需水量。

观测时段内，方案1地下水位最大变幅为3.6 m，最低水位为373.9 m；方案2地下水位最大变幅为1.9 m，最低水位为375.1 m；方案3地下水位最大变幅为2.5 m，最低水位为374.2 m(见图6、图7)。三种方案最低水位均出现在7月28日，原因是该时刻灌溉已持续90 d且需要同时灌溉玉米、棉花及蔬菜，地下水开采量大于补给量，造成地下水位严重下降。

图6 不同方案地下水位变化趋势

图7 不同方案灌区地下水位分布图

综上所述，三个目标之间是相互竞争的关系，若要改善一方面是以牺牲其它两个目标为代价。决策者可根据自己偏重方向判断，若决策者考虑增大作物产量，则选择方案1；若决策者侧重于地下水的保护，则选择方案2；若决策者倾向于增加大经济效益，则建议选择方案3。

4 结论与讨论

为实现灌区水资源多目标优化配置，本文基于NSGA-Ⅲ和FloPy构建了一个紧密耦合的灌区水资源多目标模拟优化模型，并基于假想算例进行计算分析，验证了模拟优化模型的有效性和可靠性。所构建的灌区水资源模拟优化模型以作物产量最大、经济效益最大和地下水平均累计降深最小为目标，在考虑地下水位变幅约束的同时利用遗传算法NSGA-Ⅲ获得该问题的非劣解集。算例研究表明，基于FloPy和Pymoo可以在灌区构建紧密耦合的水资源模拟优化模型，能够同时处理经济、产量和地下水位3个目标函数之间相互竞争的复杂关系，并获得倾向不同目标的多个水资源配置方案，便于决策者根据当地实际情况进行决策。

本研究仅构建了3个目标函数，没有充分发挥NSGA-Ⅲ算法在求解多个目标优化问题方面的优势，在后续研究中将进一步考虑生态、社会等方面的目标，针对真实灌区构建考虑多个目标的水资源模拟优化模型。此外，本文仅针对一个概化的典型灌域进行地下水模拟优化模型的构建，运算相对简单，因此采用mf2005.exe执行文件进行地下水数值模拟模型的计算，在进行大型灌区模型计算时，可采用并行运算mf2k5_h5_parallel.exe执行文件以节省计算时间。