高强度玄武岩机制砂混凝土抗压强度及非线性预测模型研究
2021-07-21凌建军
凌 建 军
(中铁十八局集团建筑安装工程有限公司, 天津 300308)
机制砂混凝土已经成为解决天然河砂匮乏难题的重要手段,对其配合比进行优化具有重要意义,除此之外,如何根据材料配比预测混凝土的强度也是可促进机制砂混凝土快速发展的重要因素。
目前,国内外学者已经对机制砂混凝土的力学特性展开了较多研究,相关研究主要集中于以下几个方面:某个特定掺料配比对机制砂混凝土力学指标的影响,如刘世星[1]、徐鑫等[2]、宁成晋[3]和张敏等[4]的研究;对低标号混凝土的配比进行优化设计,如黄炜[5],吴小锋等[6]的研究;机制砂中某一含量对混凝土力学指标的影响,如郭维媛[7]、程小栓等[8]通过试验研究了石粉所占质量比例对混凝土的力学指标的影响,并量化了两者之间的相关数学关系;田进[9]、张亚曼等[10]通过大量试验研究了钢渣物理化学特性、含量等对混凝土力学指标的影响,并量化了钢渣对其的影响规律和程度;除此之外,部分学者还对机制砂中某一成分变化对混凝土工作特性的影响展开了深入研究,如施忠旗等[11]通过室内试验探讨了石粉的质量比例对混凝土成形过程中放热特性进行了研究,确定了其早期的放热系数。以上专家学者的研究成果可为机制砂混凝土的工程实践提供较好的试验依据和理论指导,但由于上述研究中分析的因素相对较少,并没有综合考虑机制砂掺料全因素对其抗压强度影响。同时,上述因素并未对试验结果进行进一步分析,基于试验结果建立混凝土强度预测方法对于机制砂混凝土的工程应用具有重要意义。
基于此,采用室内正交试验对高强度玄武岩机制砂混凝土抗压特性进行了研究,分析了机制砂掺入量、钢渣掺入量、粉煤灰掺入量、水泥掺入量等因素对其7 d、28 d和56 d抗压强度的影响,探讨了各因素影响显著性;在此基础之上,对比分析了不同阶数函数对抗压强度的预测效果,并采用三阶非线性函数建立并验证了机制砂混凝土抗压强度的预测模型。
1 试验材料及方案
1.1 机制砂制备
机制砂选自云南省杨柳至宣威高速公路项目2标段主线工程,该工程全长9.62 km,设计速度为100 km/h。全线包含桥梁工程近20余座,隧道工程近4 km,对混凝土需求量极大。宣威市境内没有大河,又是在旅游业大省云南,环境保护相当严格,因此没有河沙可利用。
机制砂混凝土作为解决天然河砂匮乏难题的重要手段,会对该工程顺利进行提供便利条件。根据前期的地质调研和外围测验表明:该工程中隧道开挖而出的玄武岩节理发育良好,成分、颗粒形态及质地硬脆。因此,可将隧道开挖得到的玄武岩进行资源再利用,制成机制砂用于混凝土制备。
通过自主研发的制砂机生产出玄武岩机制砂,能够满足机制砂颗粒级配、含泥量、含粉量等要求,其主要参数如表1所示。

表1 玄武岩机制砂主要物理化学参数
其中,其颗粒级配如表2所示,级配曲线如图1所示。由图可知,颗粒级配能够达到规范要求,可作为高强度混凝土掺料使用。

表2 颗粒级配表

图1 机制砂颗粒级配
1.2 其他试验材料
(1) 水泥:试验中采用云南省某水泥厂生产的P.O 42.5R级水泥,经过测定其28 d实测抗压强度达到50.1 MPa,满足试验要求。
(2) 试验用砂:天然砂为云南省杨宣周边河砂。
(3) 石子:最大的粒径为30.6 mm,且整体颗粒级配连续(4.75 mm~9.50 mm占25%,9.5 mm~19.0 mm占55%,19.0 mm~31.5 mm占20%组合)。
(4) 水:自来水。
(5) 粉煤灰及钢渣:试验中采用II级粉煤灰和S75级钢渣粉,具体性能如表3与表4所示。

表3 粉煤灰的性能指标

表4 钢渣粉的性能指标
(6) 外加剂:重庆天耀建材有限公司生产的TY-J25缓凝剂。
1.3 试验因素及水平
根据前人研究成果和混凝土各掺料材料的特点,以及云南杨宣混凝土工程实际对力学性能的要求,本次试验选取粉煤灰的掺量、钢渣的掺量、机制砂的掺量、天然砂和机制砂总量比例(砂率)和水胶比这五个变量作为正交试验因素。为了研究上述因素对机制砂混凝土坍落度和扩展度的影响并找出工作性能最优的配比,制定L25(65)正交试验方案[12],其中水胶比五水平为0.30、0.35、0.40、0.45、0.50;粉煤灰掺量五水平为0.05、0.10、0.15、0.20、0.25;钢渣粉掺量五水平为0.05、0.10、0.15、0.20、0.25;机制砂掺量五水平为0、0.25、0.50、0.75、1.00;砂率五水平为0.40、0.41、0.42、0.43、0.44。
1.4 试验方案及结果
试验中配比严格按照试验方案进行,试件长宽高均为15 cm,养护后进行抗压强度的测试,每个试验方案均含3组平行试验,取三组平均值为该方案最终强度。最终试验结果如表5所示。

表5 正交试验结果
通过上述试验获得试验数据后,可进一步对试验数据进行分析,研究各独立掺料掺量对不同养护时间下的力学指标的影响。为便于书写,将影响成分水胶比、粉煤灰的掺量、钢渣的掺量、机制砂的掺量和砂率,分别用b1、b2、b3、b4和b5代替。
根据试验数据,可以得到b1、b2、b3、b4和b5五个因素的试验结果方差,如表6所示。由表6中数据对比可知,水胶比的方差均较大,分别达到了68.9和42.2,影响较为显著;而砂率和机制砂掺量的方差均较小,分别为0.9和0.6及1.0和1.0。该结果与极差分析较为接近,共同说明了水胶比影响较大,而机制砂掺量和砂率产生的影响较为微弱。

表6 方差分析
2 正交试验结果分析
2.1 水胶比影响
采用单一变量法展开研究,即保持其他因素不变,只改变水胶比,对比分析不同养护龄期下强度ft随水胶比变化曲线如图2所示。由图2中曲线不难看出,随着水胶比的增大,不同养护时间下的力学指标减小,且养护时间越长,力学指标减小的幅度变得越大。分析其原因为:水胶比越大,其蒸发过程会在玄武岩机制砂混凝土的内部形成较多的孔隙,影响其整体强度;且随着养护时间的增长,混凝土中孔隙体积更大,因此强度降低更加明显。

图2 水胶比对抗压强度的影响曲线
将上述因素与试验结果拟合,不同类型拟合函数得到的方差如表7所示。

表7 拟合函数类型及方差
由表7可知,与线性拟合函数相比,多项式拟合效果较好,且3阶多项式计算方差最大,拟合效果最好。
2.2 粉煤灰掺量影响
采用单一变量法展开研究,即保持其他因素不变,只改变粉煤灰的掺入量,对比分析不同养护龄期下强度随粉煤灰的掺入量变化曲线如图3所示。分析图3可以看出,随着粉煤灰掺量的增大,不同养护时间下的抗压强度均呈现逐渐减小的趋势,不同养护龄期下,强度衰减率大体相同。究其原因:粉煤灰与水反应的效果较差,其活性比水泥较低,水化反应不理想,在混凝土硬化过程中,在一定程度上降低了混凝土的粘聚性与亲活力,使得混凝土的强度降低。
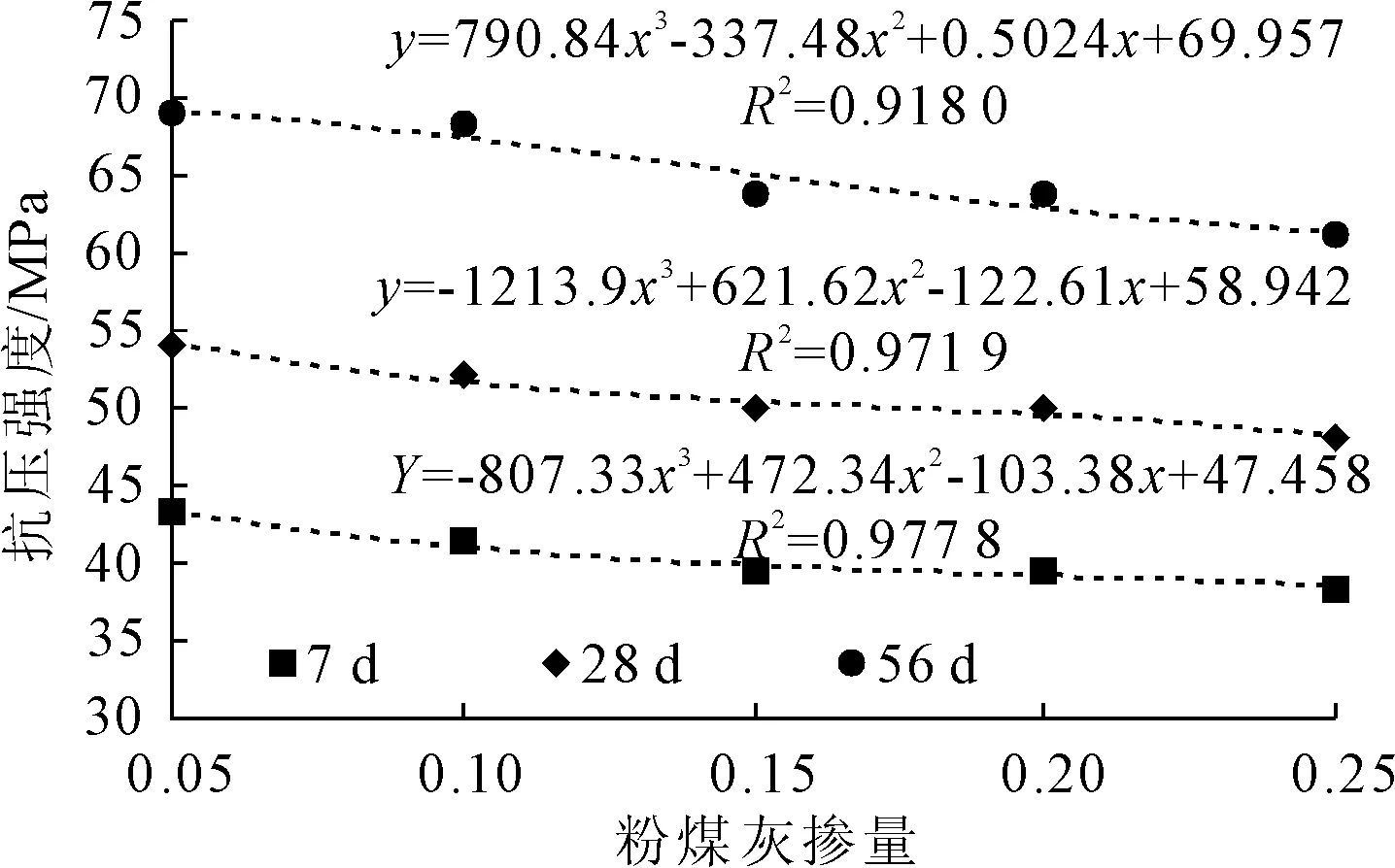
图3 粉煤灰掺量对抗压强度的影响曲线
将上述因素与试验结果拟合,不同类型拟合函数得到的方差如表8所示。
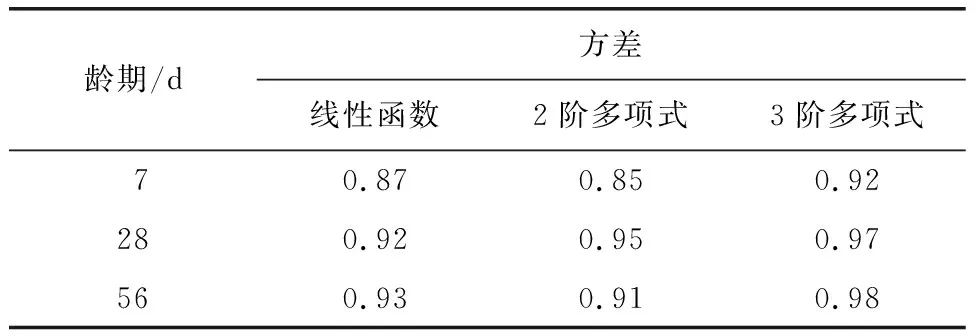
表8 拟合函数类型及方差
由表8可知,与线性拟合函数相比,多项式拟合效果较好,且3阶多项式计算方差最大,拟合效果最好。
2.3 钢渣掺量影响
采用单一变量法展开研究,即保持其他因素不变,只改变钢渣的掺入量,对比分析不同养护龄期下强度随钢渣的掺入量变化曲线如图4所示。分析图4可知,随着钢渣掺量的增加,玄武岩机制砂混凝土的抗压强度变化较小。原因在于:钢渣的掺入,调整了混凝土拌合物粘聚性和保水性等工作性能,对于混凝土流动性的影响较大,而对于抗压强度的影响较小。

图4 钢渣掺量对抗压强度的影响曲线
将上述因素与试验结果拟合,不同类型拟合函数得到的方差如表9所示。

表9 拟合函数类型及方差
由表9可知,与线性拟合函数相比,多项式拟合效果较好,且3阶多项式计算方差最大,拟合效果最好。
2.4 机制砂掺量影响
采用单一变量法展开研究,即保持其他因素不变,只改变机制砂的掺入量,对比分析不同养护龄期下强度随机制砂的掺入量变化曲线如图5所示。
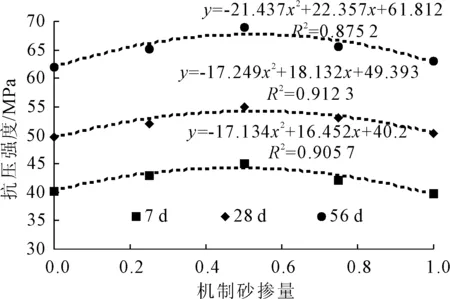
图5 机制砂掺量对抗压强度的影响曲线
由图5可以看出,随着机制砂的增大,不同养护龄期下玄武岩机制砂混凝土的抗压强度呈现出先增大后减小的趋势,在掺量为75%时,混凝土抗压强度达到最大,故在施工时应注意机制砂的掺量。
将上述因素与试验结果拟合,不同类型拟合函数得到的方差如表10所示。
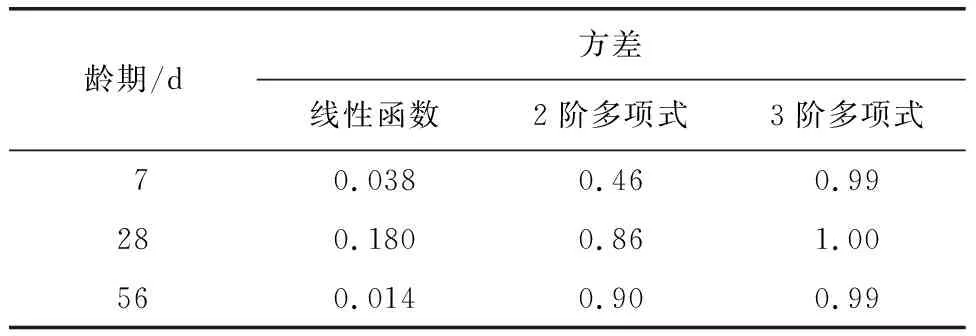
表10 拟合函数类型及方差
由表10可知,与线性拟合函数相比,多项式拟合效果较好,且3阶多项式计算方差最大,拟合效果最好。
2.5 砂率影响
采用单一变量法展开研究,即保持其他因素不变,只改变河砂和机制砂总量的掺入量,对比分析不同养护龄期下强度随河砂和机制砂总量的掺入量变化曲线如图6所示。

图6 砂率对抗压强度的影响曲线
由图6可知,随着河砂和机制砂总量的增大,不同养护时间下的强度均呈现逐渐增大的趋势,但增长趋势均较小。
将上述因素与试验结果拟合,不同类型拟合函数得到的方差如表11所示。

表11 拟合函数类型及方差
由表11可知,与线性拟合函数相比,多项式拟合效果较好,且3阶多项式计算方差最大,拟合效果最好。
3 非线性回归预测模型建立
综合不同因素下的拟合效果可知,与线性拟合函数相比,多项式拟合效果较好,且3阶多项式计算方差最大,拟合效果最好。因此,采用3阶多项式进行多元回归,建立不同养护龄期下的玄武岩机制砂混凝土抗压强度预测公式。
将水平下水胶比、粉煤灰掺量、钢渣掺量、机制砂掺量及砂率数值分别用x1、x2、x3、x4、x5代替,假定不同养护龄期下抗压强度yt的非线性回归模型为:
(1)

(2)
上式中共计15个未知数,将不同养护龄期的试验结果带入上式中则可得到回归方程中系数如表12所示。

表12 回归方程系数表
公式计算值与实测值对比如图7所示。

图7 计算值与实测值对比图
由图7可知,本文建立的公式计算得到的抗压强度与实测抗压强度分布于y=x线附近,说明两者较为接近,预测效果较好。
4 非线性回归预测模型验证
为验证本文建立预测方法的准确性,进行了5组试验,具体方案如表13所示。
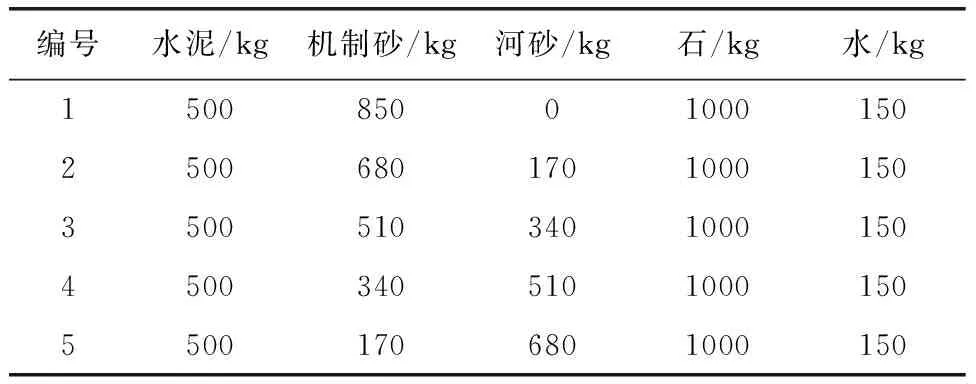
表13 具体方案表
除此之外,引用其他学者试验结果进行验证[13-14],对比试验结果及计算结果如图8所示。
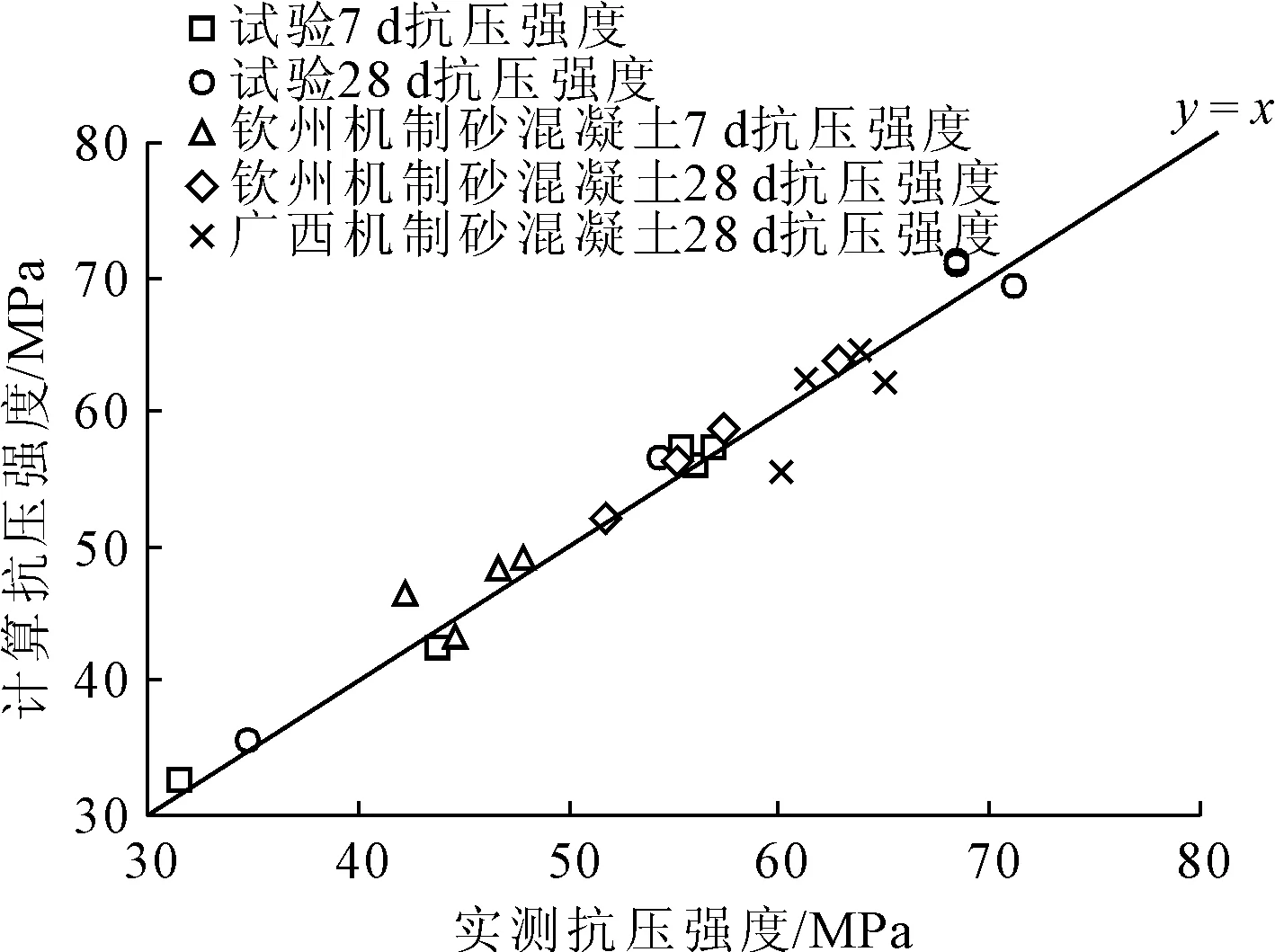
图8 试验结果与计算结果对比图
由图8可知,试验结果与本文建立的方法计算结果较为接近,本文建立的方法计算效果较好。但由于受到地域限制,不同地区机制砂特性有较大差异。因此,其他区域机制砂混凝土强度预测效果与试验数据预测效果相比略差。实际应用时,需利用相关数据对提出模型进行验证和完善。
5 结 论
采用室内正交试验对高强度玄武岩机制砂混凝土抗压特性进行了研究,分析了机制砂掺量、钢渣掺量、粉煤灰掺量、水胶比等因素对其抗压强度的影响;在此基础之上,对比分析了不同阶数函数对抗压强度的预测效果,并采用三阶非线性函数建立并验证了机制砂混凝土抗压强度的预测模型。主要结论如下:
(1) 水胶比对抗压性能的影响最大;随着水胶比、钢渣掺量和粉煤灰掺量的增大,其不同龄期混凝土抗压强度逐渐降低。
(2) 随着砂率的增大,其不同龄期混凝土抗压强度升高;随着机制砂掺量的增大,混凝土抗压强度呈现先增长后降低的趋势,存在最优掺入量。
(3) 建立的预测模型精度较高,能够反映各因素对混凝土抗压强度的影响。
