基于主成分分析的黄土高填方工后沉降组合预测方法

2021-07-21于永堂郑建国

水利与建筑工程学报 2021年3期

于永堂，郑建国，黄鑫

(1.机械工业勘察设计研究院有限公司陕西省特殊岩土性质与处理重点实验室，陕西西安 710043；2.西安建筑科技大学土木工程学院，陕西西安 710055)

近年来西部黄土丘陵沟壑区为了增加建设用地，利用"削峁填沟"方式造地，由此出现了越来越多的高填方工程。高填方场地的沉降和不均匀沉降过大时会对建(构)筑物的安全及正常使用构成威胁。因此如何预测高填方场地的工后沉降，指导建(构)筑物的规划布局和合理确定的后续地面工程的建设时机，是当前高填方工程中亟待解决的关键问题之一。黄土高填方场地的原地基地质条件的复杂性，填筑体荷载的多变性，外部环境的不确定性，使得工后沉降的理论计算值与实测值往往存在较大差异，实际工程中仍多采用基于实测数据外推预测的经验模型方法。当采用经验模型方法进行工后沉降预测时，工后初期的实测沉降历时数据较少或工后沉降观测时间较短，这时直接采用单一模型进行预测，往往会出现拟合效果好而预测效果差的情况。因此，为了提高预测精度，常采用组合预测方法，然而有时用于组合的单项模型之间会出现信息重叠现象，即存在多重共线性问题，这导致新增加单项模型并不一定总能明显提高预测精度，为此，有学者建议剔除一些仅增加少量有用信息的单项模型[1]。关于组合预测中单项模型的数量问题，Granger等[2]和Aiolfi等[3]的研究结果显示，参与组合预测的单项模型数量，一般不存在普遍适用的最优数量。此外，Aiolfi等[4]还发现，一些单项模型的预测效果并不稳定，随着观测时长的增加，先前预测效果好的模型将来可能变差，先前预测效果差的模型将来也可能会变好。因此，仅通过剔除某些单项模型的方法并不能完全解决上述问题。此外，在沉降观测初期，在数据量少的情况下，采用基于回归的组合预测模型，容易出现单项模型数量多于样本数据量的情况，还会导致回归参数无法估计等问题。

主成分分析(Principal Component Analysis，简称PCA)是用几个较少的综合指标(即主成分)来代替原来较多的指标，找出数据中最主要的元素和结构，去除数据中的噪音和冗余，将原有复杂数据进行降维，揭露隐藏在复杂数据背后的简单结构[5]。PCA最早由英国生物统计学家Pearson[6]在1901年在对非随机变量进行讨论时引入，随后数学家Hotelling[7]将其推广至随机变量。之前PCA主要用于计算机图像处理[8]、经济分析等领域[9]，近年有学者将PCA与逐步回归法[10]、分类回归树[11]、SPE控制图[12]、BP神经网络[13]、时间序列分析[14]、主元回归建模[15]等方法相结合进行相关预测，但PCA在工程建设领域的应用鲜有报道。

本文采用主成分分析方法对单项预测模型进行降维处理，用于解决基于回归的组合模型中单项预测模型数量多于建模数量，以及单项模型之间的多重共线性等问题，并结合某黄土高填方场地的实测沉降数据，对预测结果进行了验证。

1 主成分分析的基本思想

假设实际问题中共有p个指标X1，X2，…，Xp，每个指标共有n个样本，组成n×p阶的数据矩阵如式(1)所示。

(1)

对原变量指标X1，X2，…，Xp作线性组合，经降维处理后，得到新变量指标(综合指标)为Z1，Z2，…，Zm(m≤p)，原变量指标与新变量指标之间的关系如式(2)所示。Z1，Z2，…，Zm分别为原变量指标X1，X2，…，Xp的第1，2，…，m主成分。

(2)

式(2)满足如下条件：

(1) 主成分Zi与Zj(i≠j；i，j=1，2，…，m)相互独立，无重叠的信息，即Cov(Zi,Zj)=0。

(2) 主成分方差满足Var(Z1)≥Var(Z2) ≥…≥Var(Zm)，即Z1是与X1，X2，…，Xp一切线性组合中方差最大者，含有最大的信息量；Z2是与Z1不相关的X1，X2，…，Xp的所有线性组合中方差最大者；依此类推得到各主成分……；Zm是与Z1，Z2，…，Zm-1都不相关的X1，X2，…，Xp的所有线性组合中方差最大者。

2 基于主成分分析的组合预测模型建模

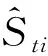
(3)

式中：w0为常数项；wi(i=1，2，…，m)为第i种单项模型的权重系数；εt为随机扰动项(随机误差)。当主成分分析法进行回归组合预测的主要步骤如下：

(4)

由m个单项模型组成n×m维数据矩阵如式(5)所示。

(5)

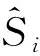
(6)

由式(6)计算得到相关系数矩阵R=(rij)m×m如式(7)所示，该矩阵为对称矩阵。

(7)

(3) 计算特征值与特征向量。首先运用Jacobi迭代方法计算特征方程1λE-R1=0，求出特征值并按大小顺序排列(λ1≥λ2≥…≥λm≥0)，然后求出特征值λi对应的特征向量Ui(i=1，2，3，…，m)如式(8)所示。

Ui=[u1i，u2i,…,umi]′

(8)

由特征向量Ui组成的主成分系数矩阵U如式(9)所示。

(9)

以特征向量的分量值为权数，将标准化的变量指标进行加权得到第i个主成分。主成分与原变量指标之间的关系如式(10)所示。

Z=U′S=[Z1Z2…Zm]T=

(10)

(4) 建立多元线性回归模型。在多元回归分析中，最优的回归模型一般要求表征模型拟合效果的似然函数最大化，模型中未知参数个数最小化，因此，本次对主成分的筛选采用赤池信息量准则(Akaike Information Criterion，AIC)[16]，计算方法见式(11)。

AIC=2k-2lnL

(11)

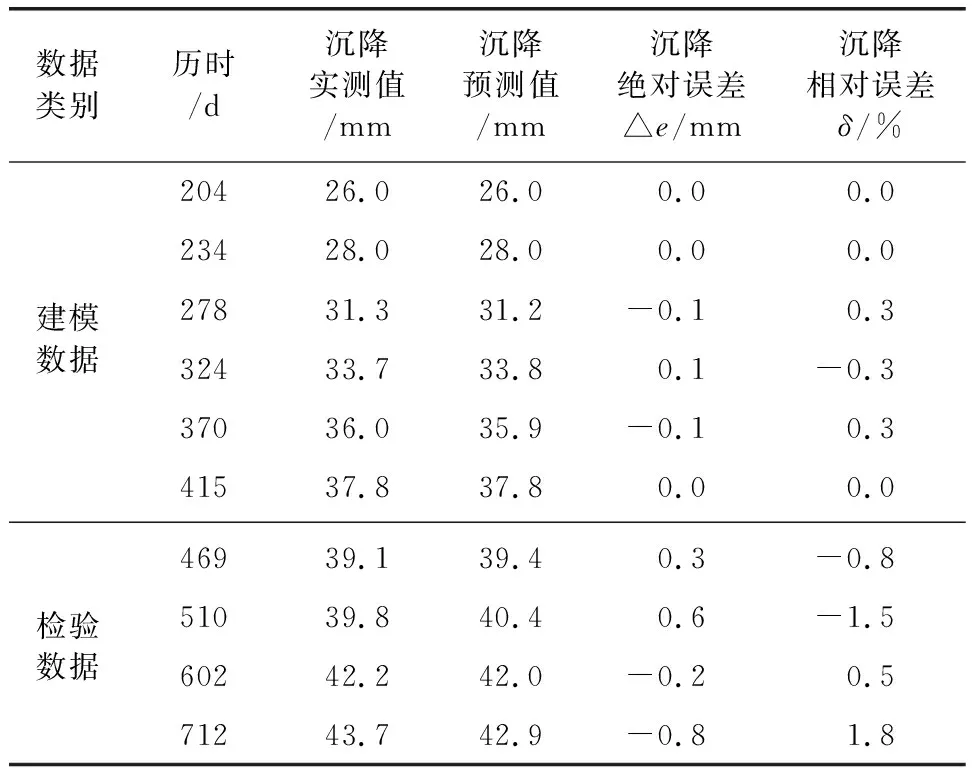
式中：k为模型参数个数；L为似然函数。当进行多元回归组合建模时，每一步新引入一个主成分，若AICi+1>AICi，则剔除新引入的主成分Zi+1，若AICi+1

根据上述思路，现举例如下：首先对第1主成分作线性回归，计算回归模型参数a0、a1，进行显著性检验，计算AIC值，记为AIC1。

(12)

在式(12)中增加第2主成分Z2，计算AIC值，记为AIC2。若AIC2

(13)

3 实例分析与效果检验

陕北某黄土高填方工程地处黄土丘陵沟壑区，属于采用削峁填沟方式的造地工程，原地基采用强夯法处理，填筑体采用分层碾压法处理，料源黄土的含水率分布区间为8%～20%；干密度分布区间为1.53 g/cm3～1.89 g/cm3。典型监测点O5共15期沉降数据，本次采用前5期数据，采用Logistic模型[17](模型1)、Gompertz模型[18](模型2)、Usher模型[19](模型3)、Weibull 模型[20](模型4)、MMF模型Ⅰ[21](模型5)、MMF模型Ⅱ[22](模型6)、改进Richards模型[23](模型7)、Janoschek模型[24](模型8)、Knothe模型[25](模型9)、改进Knothe模型[25](模型10)、邓英尔模型[26](模型11)、Spillman模型[27](模型12)建模外推预测10期数据，预测结果如表1所示。可见，在数据量较少的情况下，各模型的预测效果均较差，存在单项模型收敛过早或过晚等问题。

表1 典型监测点的工后沉降实测值及预测值

为了提高预测精度，采用表1中前6期预测数据作为PCA组合预测模型的建模数据，采用MATLAB R2014b软件中的corrcoef(A)函数计算各单项模型方法之间的相关系数，采用[pc,score,latent,tsquare]=princomp(A)函数计算特征向量pc(主成分系数)、主成分值Score、特征值(从大到小排列)latent、每个样本点霍特林(Hotelling)T2统计量tsquare。由表1中数据计算得到各单项预测方法之间的相关系数如表2所示。由表2可看出，各单项模型的预测数据之间的相关系数较高，表明在显著性水平条件下，这些自变量之间的线性相关性较高，即各单项模型之间存在多重线性相关性。这主要是多数单项模型预测值与实测值线性相关，进而导致各模型之间也线性相关。

表2 各预测模型之间的相关系数

各单项模型的主成分系数和新坐标系下各主成分的值，如表3和表4所示。将表1中第7、8、9、10期各模型的预测数据作为组合模型的检验数据，并转化为主成分值，计算过程如表5、表6所示。

表3 主成分系数

表4 建模数据在新坐标系下主成分值

表5 检验数据在新坐标下主成分值的计算结果

续表5

表6 检验数据在新坐标系下的主成分值

从表4中可以看出，在新坐标下，最后7个主成分不包含任何信息，原数据维数得到降低，其中不为0的主成分值共5个。逐次增加主成分值Z1、Z2、Z3、Z4、Z5，采用数据分析软件EViews 10建立多元线性回归模型，求解模型参数a0，a1，…，ai。当主成分值为5个和4个时二者AIC值相差不大，为简化计算防止过拟合，主成分数量取为4个，组合模型见式(14)。

(14)

表5中第i期(i=7、8、9、10)去中心化方法为各模型第i期预测值减去前6期均值，将表6中Z1、Z2、Z3、Z4值带入式(14)可求得组合模型预测值。组合模型预测效果与各单项模型的预测效果比较如图1所示。组合模型预测误差统计结果如表7所示。

图1 组合模型与单项模型的预测曲线

表7 组合模型沉降预测误差统计结果

本次以第415 d为起点，对后续第469 d、510 d、602 d、712 d，共4期数据采用组合模型进行预测，预测数据的时间跨度为297 d。由预测误差分析结果可知，在检验数据时间跨度是建模数据时间跨度1.4倍的情况下，组合模型预测值与实测值吻合较好，绝对误差Δe(预测值与实测值之差)在±1 mm内，相对误差在-1.5%～1.8%之间，表明基于PCA的组合预测模型能大幅度提高预测精度。