基于改进的经验模态分解的后视镜驱动器故障诊断方法

2021-07-21朱少成

河南科技大学学报(自然科学版) 2021年6期

高丰，朱少成，罗石

(江苏大学汽车与交通工程学院，江苏镇江 212013)

0 引言

电动后视镜凭借其调节方便和驻车收缩等功能特点，在小型轿车中逐渐普及。后视镜驱动器作为电动后视镜核心部件，相比于传统机械后视镜，在驱动器部分发生故障的概率较高。电动后视镜驱动器中存在的微小故障将会导致调节角度不到位及视野受限等问题，从而威胁驾驶安全。因此，有必要对电动后视镜的驱动器进行故障诊断研究。

目前，针对旋转机械的故障诊断常用的信号时频分析方法有: 傅里叶变换[1](Fourier transform,FT)、短时傅里叶变换[2](short time Fourier transform,STFT)、维格纳分布[3](Winger-Ville distribution,WVD)和小波变换[4](wavelet transform,WT)等。文献[5]使用傅里叶变换结合多滤波器进行机械故障诊断，但傅里叶变换是基于线性系统和稳定信号的假设前提下应用的方法，存在一定的局限性。针对传统傅里叶变换的不足，文献[6-8]将STFT应用在机械故障诊断中，但是该方法同时受到时间分辨率与频率分辨率的约束。文献[9-11]提到了小波变换在机械故障诊断中的应用，但是小波基函数的选择对结果影响较大。经验模态分解[12](empirical mode decomposition, EMD)方法依据输入振动信号自身的特点，自适应地将振动信号分解成若干个固有模态函数之和，不依赖窗口与基函数的选取。文献[13-14]研究了EMD方法在电机故障诊断及轴承故障诊断中的应用。

基于上述文献研究，本文提出了改进的集成经验模态分解算法(ensemble empirical mode decomposition,EEMD)与自回归模型(autoregressive model,AR)功率谱估计结合的后视镜驱动器故障诊断方法。首先，使用EEMD算法将后视镜驱动器振动信号分解成若干个本征模态函数(intrinsic mode function,IMF)信号，通过峭度谱与相关系数结合的方法筛选出有效的IMF分量。其次，对有效IMF分量进行AR功率谱估计，得到AR累加谱后，再利用特征频率的平均能量进行模式分类与识别。最后，比较了几种现有模型进行故障诊断的实时性与识别率，总结了EEMD-AR-支持向量机(support vector machine,EEMD-AR-SVM)方法进行电动后视镜驱动器故障诊断的优势。

1 算法理论

1.1 集成经验模态分解

EEMD方法[15]是对经验模态分解方法[16]的改进，主要特点在于通过加入高斯白噪声取平均值，求得本征模态函数成分来抑制 EMD 方法中存在的模态混叠现象。其主要步骤为：

(Ⅰ)对于后视镜驱动器的振动信号S(n)，添加均值为0、标准差为δ的白噪声序列mi(n)，得到加噪信号的表达式为Si(n)=S(n)+mi(n)。其中：Si(n)为第i次加入白噪声的振动序列信号；mi(n)为第i次加入的白噪声序列。

(Ⅱ)利用经验模态分解的方法，将Si(n)分解成若干个IMFi与一个余项函数ri(n)。

针对后视镜驱动器振动信号的特点，本文设定EEMD方法中的N为15，σ设置为0.2，一方面符合了 EEMD 方法设定高斯白噪声与加噪次数的要求；另一方面能够保证在不引起模态混叠现象的同时，引入较小的噪声，减少对原始信号的影响[17]。

1.2 AR功率谱估计方法

传统的谱估计方法对数据长度有较高的要求，其分辨率取决于数据长度，相比于现代谱估计方法，其分辨率较低，且容易受到窗函数的影响，发生频谱泄露，产生虚假的峰值。现代谱估计方法能够弥补传统谱估计分析的局限之处。其中，AR谱估计是较为常用的一种分析方法[18]，由于其频率分辨率高以及计算量小的特点，得到了广泛的研究和应用。对于驱动器振动信号序列S(n)，其 AR 模型可以表示为：

(1)

其中：u(n)为白噪声序列；p为 AR 模型的阶数；ak(k=1,2,…,p)为 AR模型的参数。由式(1)可得 AR 模型的 Yule-Walker 方程[19]为：

(2)

(3)

若想求得信号S(n)的功率谱Px(ω)，就要求得 AR 模型参数ak以及方差σ2。这样，谱估计问题可以转化成 AR 模型的参数估计问题。

本文选择 AR 模型的阶数p为12，能够使得谱估计分辨率适中，既不会因为阶数低导致估计结果平滑，也不会因为阶数高而导致振荡[20]。

1.3 峭度与相关的有效IMF分量筛选

相关系数表征了一个序列与另一个序列的相关程度[21]。本征模态函数 IMF 的选择过程中，通常认为 IMF 分量与原始信号序列S(n)相关系数较大的分量为有效的本征模态分解分量；相关系数较小的分量为虚假的本征模态分量，应当剔除。时域特征中的峭度系数对偶发冲击信号敏感，若振动信号中存在强烈的冲击，则该指标会偏高；若振动信号较为平稳，则其峭度系数较小。观察后视镜驱动器的振动信号，在断齿与外壳干涉这两类故障样品中都存在冲击成分。较高的峭度系数则可以反映振动信号存在较多的冲击故障信息，利用峭度系数，结合相关系数，可以剔除掉虚假的 IMF 分量。

计算相关系数与峭度系数过程[22]为：

(4)

(5)

经过大量实验分析，本文设定相关系数的阈值为0.3，峭度系数的阈值为4，若分解后的 IMF 分量与原始信号的相关系数大于0.3，并且峭度系数小于4，可认为该 IMF 分量为有效的 IMF 分量；而不满足该判定条件的分量则被认定为虚假的 IMF 分量，应当被剔除。筛选出的每一阶有效 IMF分量进行AR功率谱估计，调整相加后得到信号的 AR 累加谱，对 AR 累加谱特征频率与振幅进行特征提取，以此作为特征向量进行分类器的训练，从而可以分别对健康、断齿和外壳干涉的后视镜驱动器进行故障检测。

2 实验分析

2.1 实验设备及数据采集

搭建如图1所示的后视镜驱动器故障检测台架及样品内部结构。图1a为测试工装，中间通过三爪卡盘固定待测后视镜驱动机构，电源接口输入不同的电平可以驱使后视镜驱动机构在x轴和y轴两个方向运动。图1b展示了振动信号放大器，选择的放大倍数为100 倍；加速度振动传感器放置于后视镜驱动器表面，测量振动的加速度信号。输入电压控制在16 V，采样频率设置为5 kHz，为保证采样信号中含有若干个冲击故障周期，设置采样时间为1 s，每个样本含有数据采样点个数为50 000 个。图1c描述了待测试后视镜驱动器样本的内部结构，主要由1对对称的微型电动机、2套减速齿轮组合与电源接口组成。其中，每套减速齿轮组合均包括：2组蜗轮蜗杆减速机构、1组圆柱齿轮减速机构和1组圆锥齿轮减速机构，进而构成四级减速系统。

(a) 后视镜驱动器故障检测自动化工装 (b) 振动信号放大器 (c) 待测试后视镜驱动器样本内部结构

2.2 算法与应用分析

首先通过振动传感器与测试工装，分别获取健康驱动器、断齿驱动器和外壳干涉驱动器样本的振动信号，观察其时域信号波形与频谱。图2为后视镜驱动器样本时域振动信号。

(a) 断齿驱动器时域信号 (b) 健康驱动器时域信号 (c) 外壳干涉驱动器时域信号

从图2a可以看出：故障后视镜驱动机构振动信号的时域波形中含有一个11 Hz、幅值约为0.35 V的振动冲击，结合对实物的拆解可以发现，该故障是由于涡轮蜗杆出现断齿现象所产生，导致后视镜驱动器在时域信号中展现出周期性的冲击，具有振动信号的调制现象。图2b描述了健康后视镜驱动器的时域波形，能观察到振动信号相对平稳，不包含冲击的成分。图2c描述了外壳干涉驱动器的时域信号波形，可以看到在0.2 s处出现了一个相对幅值较高的冲击成分，该冲击成分是由于内部的机械结构与外壳干涉所产生的结果。

分别对3种样本的振动信号进行 EEMD 分解，根据1.3节中设置的阈值进行有效 IMF 分量的筛选，其中峭度系数与相关系数如图3所示。健康驱动器的第1、2、3阶 IMF 曲线峭度系数超过阈值；断齿驱动器的第1、2、3、4、5、6、7、9、10阶 IMF 曲线峭度系数超过阈值；外壳干涉驱动器的第1、2、3、11阶IMF曲线峭度系数超过阈值。图3b描述了相关系数曲线，3类样本的第1、2、3、4阶的 IMF 曲线达到了相关系数的阈值要求。

(a) 本征模态函数峭度系数 (b) 本征模态函数相关系数

选取故障后视镜驱动器振动信号的有效IMF分量的条件为：Cori≥0.3∩Cq>4。通过上述方法遴选出有效 IMF 分量：断齿驱动器振动信号的 IMF1、 IMF2、 IMF3和IMF4；健康驱动器的IMF1、IMF2和IMF3；外壳干涉驱动器的 IMF1、IMF2和IMF3。对筛选出的有效 IMF 分量进行 AR 功率谱估计。本文采取的 AR 谱估计方法是Yule-Walker的功率谱估计方法。

图4a描述了断齿驱动器样本有效 IMF 分量的 AR 功率谱估计曲线，在其中 IMF2、 IMF3和IMF4 这3个分量上能够观察到在2 000 Hz处有一个峰值。图4b描述的健康驱动器的 IMF3 在3 100 Hz处有一峰值，其他 IMF 曲线较为平滑。图4c所示的外壳干涉驱动器的三阶 IMF 曲线在3 600 Hz处有一个峰值。

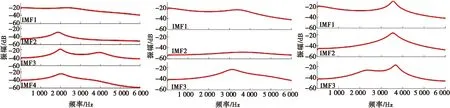
(a) 断齿驱动器IMF的AR功率谱估计 (b) 健康驱动器IMF的AR功率谱估计 (c) 外壳干涉驱动器IMF的AR功率谱估计

对筛选出的有效信号的 IMF 分量累加后进行修正，得到图5的结果。

图5描述了3种样本有效 IMF 分量的 AR 累加功率谱估计曲线。由图5可知：断齿驱动器特征频带递增区间为1～1 953 Hz，振幅峰值达到-72 dB；健康驱动器的特征频带递增区间为1～3 174 Hz，振幅峰值达到-96 dB；外壳干涉驱动器特征频带递增区间为1～3 613 Hz，振幅峰值达到-47 dB。

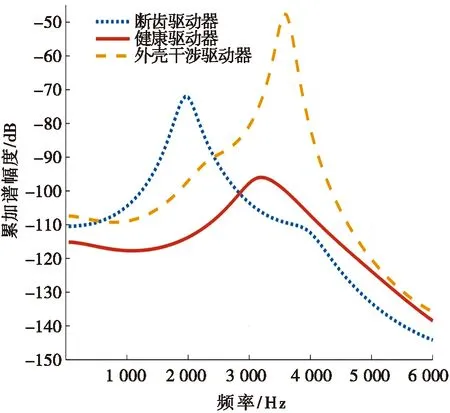
图5 有效IMF分量的AR累加谱

提取 AR 累加谱中的特征频率点与峰值点，输入多分类SVM中进行学习与预测[23]，选择的SVM种类为线性SVM分类器，5 折交叉验证，其散点图如图6所示。由图6可知：断齿驱动器样本未出现分类不正确的情况；健康驱动器样本与外壳干涉驱动器样本预测结果有一部分出现了混叠，表示分类器在进行这两类样本分类的过程中出现了错误的结果。造成错误预测分析的原因如下：断齿驱动器的 AR 累加谱特征峰值频率和振幅与健康、外壳干涉驱动器样本的距离较大，因此能够得到一个客观的分类准确率；而健康驱动器样本与外壳干涉驱动器样本有一小部分的特征重合，距离较小，导致分类误判。

图6 SVM对3类驱动器样本的学习与预测

SVM分类结果如表1所示，总体分类的准确率为93.9%，不正确分类结果中，有7.8%的外壳干涉驱动器样本被误分类为健康状态；有9.3%的健康驱动器样本被误分类为外壳干涉故障；针对断齿驱动器样本的分类达到了100%的准确率。

表1 SVM分类结果 %

本文对EEMD-AR-SVM 模型与其他分类模型进行实时性与预测准确性的比较[24-25]。实验硬件环境配置如下：Intel-i7-8700K处理器，3.70 GHz主频，32 G内存。表2给出了几种算法对3类驱动器样本振动信号识别的准确率与时效性。

表2 模型准确率与耗时对比图

从表2可以看出：根据时频域特征提取结合支持向量机分类的方法，对后视镜驱动器样本进行分类识别，仅能达到83.7% 的准确率，添加特征降维的方法虽然减少了消耗时间，但是由于维数降低，导致识别准确率反而下降；单纯的 EMD 方法在提取 IMF 后，将其作为特征向量进行支持向量机的分类，则会因为维数太过巨大，引起维度灾难的问题，导致消耗时间延长，并且无法得到一个较为精确的识别结果。本文提出的模型方法以消耗计算资源的代价能够获得超过90% 的识别准确率，可以实际应用于汽车电动后视镜驱动器生产与质量检测的过程之中。