金属矿开采深度对留设矿柱稳定性的影响

2021-07-21胡娟新张云朝

中国金属通报 2021年14期

胡娟新，张云朝

（1.保利新联爆破工程集团有限公司，贵州贵阳 550002；2.山东鼎安检测技术有限公司，山东济南 250000）

我国是世界上主要的金属矿生产国和消费国，且已探明的金属资源储量及其开采量均居世界前列。依据国家统计局统计[1]，截止2019年，我国金属储量在230亿左右，金属矿山数量有900多座，年开采量为4亿吨左右。长期以来，金属在我国能源消费结构中占据显著地位，是我国现代化经济建设强有力的重要保障之一。

近些年以来，金属矿开采强度越来越大，使得矿井发生灾害的频次及灾害程度越来越严重，其中留设矿柱失稳发生的灾害尤为突出。因此，留设矿柱的稳定性现已成为制约矿井安全高效开采的重要问题，也是众多科技工作者关心的热点问题。费鸿禄等[2]采用FLAC数据软件模拟了矿柱爆破回采过程中对留设矿柱的稳定性影响[1]。

据不完全统计，在这些灾害事故中，关于留设矿柱发生的灾害问题尤为突出。为此，开展关于矿层埋深对留设矿柱的稳定性影响至关重要。针对该问题，采用数值模拟软件，建立不同埋深及开采宽度下金属矿开采数值模型，获得了留设矿柱的支承应力、变形及弹性应变能演化规律，进而探讨了留设矿柱稳定性。

1 金属矿开采数值模型及其模拟方案

1.1 数值模型的建立

采用FLAC3D 建立深部采场模型，模型中X 方向为工作面布置方向，Y 方向为工作面推进方向。模型采用位移控制边界，限制模型X、Y 方向水平移动，限制模型Z 方向底面边界垂直位移，模型Z 方向顶面为自由边界，施加竖直均布荷载以模拟上覆岩层自重载荷，给模型施加的重力加速度取9.8m/s2。同时为了消除边界效应的影响在模型两边界处各留设40m 矿柱，建立的数值计算模型如图1 所示。

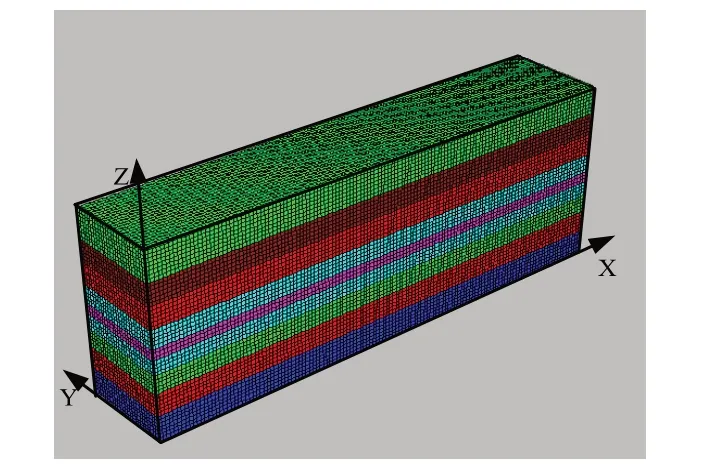
图1 三维数值计算模型

1.2 数值模拟方案

根据数值模拟研究矿体层埋深对围岩及其矿柱稳定性影响的目的，同时，为了便于研究分析，将深部开采留设矿柱宽度固定为100m。模拟矿层埋深600m、800m、1000m、1200m 及1500m等不同埋深时，揭示地下金属开采对留设矿柱变形、应力及能量演化规律，以探究埋深对留设矿柱及其稳定性的影响。在开采面布置方向上开采两个类条带，留设一个金属矿柱，建立的模型几何结构如图2 所示，制定的地下开采数值模拟方案如表1 所列。

表1 开采数值模拟方案

图2 模型几何结构

（1）矿层埋深600m 时，分别取开采宽度为80m、100m、120m 及140m 进行数值模拟。

（2）矿层埋深800m 时，分别取开采宽度为80m、100m、120m 及140m 进行数值模拟。

（3）矿层埋深1000m 时，分别取开采宽度为80m、100m、120m 及140m 进行数值模拟。

（4）矿层埋深1200m 时，分别取开采宽度为80m、100m、120m 及140m 进行数值模拟。

（5）矿层埋深1500m 时，分别取开采宽度为80m、100m、120m 及140m 进行数值模拟。

备注：表3.2 中编号600～100 表示金属层埋深600m 时，条带开采宽度100m。

数值模拟计算结束后，采用Origin 等后处理软件，对模拟计算结果进行处理，获得不同模拟方案下留设矿柱变形、应力及弹性应变能分布曲线，从而揭示随矿层采深的逐渐增加开采诱发矿柱失稳机制。

2 金属矿开采数值模拟结果分析

基于上述数值模拟方案，模拟监测了不同埋深条件下，矿层开采过程中矿柱应力、变形及能量变化。

2.1 留设矿柱支承应力演化规律分析

数值模拟不同埋深及不同采宽条件下，监测开采过程中留设矿柱100m 宽度范围内的支承压力分布特征，如图3 所示。

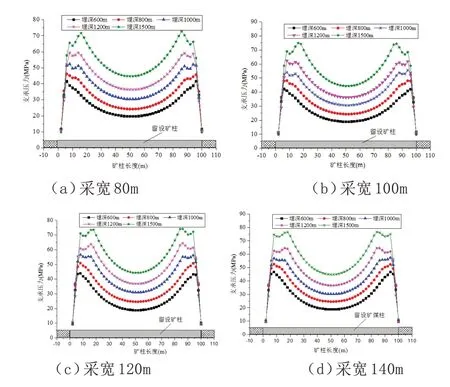
图3 不同埋深及采宽时留设矿柱支承压力分布

由图3 可知，当矿体开采宽度为120m 时，矿层埋深600m 最大支承压力值为43.9MPa，矿柱核区最小应力值为18.8MPa；矿层埋深1200m 最大支承压力值为63.7MPa，矿柱核区最小应力值为36.8MPa；矿层埋深1500m 最大支承压力值为73.6MPa，矿柱核区最小应力值为44.3MPa。对比埋深600m 和1500m 可知，矿柱埋深1500m 最大支承压力值和核区最小应力值分别是金属柱埋深600m最大支承压力值和核区最小应力值的1.68倍和2.36倍。

2.2 留设矿柱变形规律分析

在模拟开采过程中，对不同埋深条件下的留设100m范围内的矿柱变形量进行了监测，分析不同采深条件下矿柱竖直变形分布特征，并对不同采宽条件下的矿柱竖直位移进行分析，留设矿柱最大竖直位移量及留设矿柱平均竖直位移量分布分别如图4和图5所示。

由图4 和图5 分析可知，对同一开采宽度而言，通过矿层埋深800m、1000m、1200m、1500m 与矿层埋深600m 相比较可知，留设条带矿柱随着埋深的增加，矿柱最大竖直位移量分别增加了10.803mm、24.26mm、37.852mm、67.081mm，分别占矿层埋深600m 的条带矿柱最大竖直位移量的百分比为22.2%、49.8%、77.8%、137.8%；条带矿柱最大竖直位移量随着金属层开采深度的增加而显著增加。

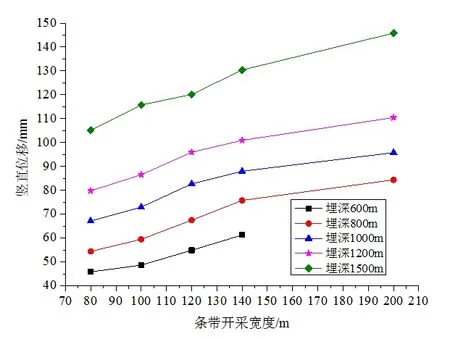
图4 不同埋深时留设矿柱最大竖直位移分布

图5 不同埋深时留设矿柱平均竖直位移量分布

同时，对于同一条带采宽而言，通过矿层埋深800m、1000m、1200m 及1500m 与矿层埋深600m 相比较可知，留设条带矿柱的平均竖直位移量分别增加了11.411mm、25.248mm、40.419mm、64.89mm，分别占矿层埋深600m 的条带矿柱平均竖直位移量的百分比为26.6%、59.5%、94.3%、151.2%，较条带矿柱最大竖直位移量增加百分比显著增加。

2.3 留设矿柱弹性应变能演化规律分布

大量研究表明，矿体动力失稳诱发冲击一般发生于处于脆性状态的矿体之中，此时，矿体处于三向受力状态，受复杂地质运动的影响，矿体中积蓄了大量的弹性应变能，而且受采动应力及顶板运动叠加等附加应力的影响。

根据广义胡克定理可知，三向受力状态下矿体内储存的弹性应变能计算公式为：

式中：E——弹性模量。µ——泊松比。σ1——最大主应力。σ2——中间主应力。σ3——最小主应力。

基于广义胡克定理矿体三向受力状态下的弹性应变能公式（1），运用FISH 语言编写受采动影响的矿体弹性应变能分布计算命令，计算得出不同埋深及采宽条件下的矿体弹性应变能分，导出条带开采后留设矿柱100m 宽度范围内的弹性应变能并生产曲线，弹性应变能密度分布如图6 所示。

图6 不同埋深及采宽时留设矿柱弹性应变能密度分布

由图6 分析可知，对于同一条带开采宽度而言，通过金属层埋深800m、1000m、1200m 及1500m 与埋深600m 相比较可知，条带金属柱最大弹性应变能值分别增加了44.6kJ/m3、82.6kJ/m3、146.9kJ/m3及241kJ/m3，分别占埋深600m 时留设矿柱最大弹性应变能值的百分比为32.1%、59.4%、105.7%及173.4%，矿柱最大弹性应变能随着矿层埋深的增加而显著增加。随着矿层埋深的增加，矿柱两侧弹性应变能峰值之间的距离逐渐减小，矿柱内所储存的弹性能越大，矿柱的稳定性显著减弱。