直升机载旋转式合成孔径雷达成像振动误差补偿算法

张 俊 王 伟 向 聪 相 飞 宋文青

(西安电子工程研究所 西安 710100)

0 引言

近年来，旋转式合成孔径雷达作为一种新型成像模式，凭借其短重访周期与灵活成像体制在灾难救援与战场监视等领域引起了广泛关注[1-6]。尽管ROSAR已经进行了多年的发展研究，但在实际应用中仍然存在不少限制与困难，其中最为典型的问题就是运动平台振动误差补偿。由于ROSAR的应用平台主要为直升机，在其飞行工作期间，直升机旋翼旋转时与空气的摩擦会产生高频振动，该振动引入的相位误差往往会导致最终图像质量的恶化[7-9]。

由于直升机的振动具有周期性时变的特征，当振动特性参数未知时，往往难以通过解析式对运动误差进行精确补偿。除此之外，ROSAR复杂的斜距历程也会给相位误差的解析式推导带来困难。上述问题会导致传统算法处理后的回波误差存在空变现象，进而无法利用自聚焦算法对运动误差进行估计补偿[10]。针对上述问题，文献[11]提出了基于自适应调频基分解的正弦调频信号参数估计方法，尽管该方法对正弦调频信号的估计具有较高的精度，但其估计精度依赖于初始调频基的选取并需要多次迭代搜索，算法运算量较大，不利于工程实现，此外，该方法仅对单一振动频率的正弦信号具有较高估计精度，而实际中，平台的振动往往是至少两种不同频率振动相叠加的合成结果，因此基于自适应调频基分解的方法精度会明显下降。文献[12]则针对传统直线SAR的振动误差抑制提出了基于系统参数设计的处理方法，尽管该方法能够通过选取合适的系统参数，如波长、脉冲重复频率等来降低振动误差引入的运动相位误差量级，进而抑制振动误差对最终成像的影响，但对于振动现象较为严重的直升机平台，抑制后的振动误差仍然会对最终成像结果产生影响，需要在后续处理中将其消除。但截止目前，还未有具体的文献对ROSAR振动误差补偿方法进行详细介绍，因此研究基于数据的ROSAR振动误差补偿算法是推动ROSAR工程应用的关键所在。

针对上述问题，本文提出了一种结合多普勒Ksystone变换与相位梯度自聚焦的ROSAR成像及运动误差补偿方法，首先对直升机平台振动特性进行了详细分析并建立了包含振动误差的ROSAR信号模型。随后利用双重多普勒Keystone变换对距离徙动进行校正，该处理能够在二维频谱上消除空变相位，补偿信号回波中的剩余视频相位后，即可得到非距离依赖的振动误差相位信号，再结合加权最大似然相位梯度算法(WML-PGA)即可改善相位误差估计精度并获得聚焦良好的ROSAR图像。最后利用仿真结果对所提算法的有效性与正确性进行了验证。

1 直升机载ROSAR振动误差及回波信号模型

ROSAR系统平台在空中作业时，直升机旋翼在旋转时与空气高速摩擦会周期性地产生交变转矩，该转矩引入的机身抖动会传递到整个机身，进而使天线相位中心产生振动频率为N/T的高频振动，其中T为合成孔径时间，N表示在时间T内平台的振动次数。根据实际测量数据[13]，我们选择典型的BO105型直升机作为实验平台，结合其振动特性对接收到的信号回波进行分析处理。本文中振动误差的分析主要基于谐波运动模型，即单次谐波的振动率范围通常在[10Hz，30Hz]范围之内，振动幅度范围为[0.01g,0.15g]，其中g表示重力加速度，且有1g=10m/s2。结合上述分析，可以给出瞬时振动幅度η的表达式为

(1)

其中K表示谐波次数，Ak，Tk，Nk与φk分别表示振动幅度、合成孔径时间、振动起伏次数与第kth次谐波的初始相位，ta表示方位时间。

图1给出了ROSAR成像几何构型。天线被安装在直升机旋翼顶端，天线相位中心在高度H处，绕半径L，并以恒定角速度ω做匀速圆周运动，α为天线到场景中心的俯仰角。假定场景中有一目标点P，其在圆柱坐标系下表示为(rp，ωtp，0)。这里忽略沿角度向误差的影响，考虑到ROSAR合成孔径时间通常较短，因此可以认为在一个合成孔径内，振动误差仅会引起平台在高度向的运动误差相位。

图1 旋转式合成孔径雷达成像几何构型

结合上述分析，可知ROSAR工作过程中，实际的相位中心高度为H-η，因此可以推导得到天线相位中心的斜距历程表达式为

(2)

考虑到平台振动幅度远小于成像的斜距历程，在斜视角为0的情况下，式(2)可以被近似为

Rr(ta)≈Ri(ta)+η·cosα

(3)

其中Ri(ta)表示理想斜距，其具体表达式为

(4)

发射信号为线性调频信号，且目标散射系数为一恒定常数，可以写出信号回波的表达式为

(5)

其中τ=2Rr(ta)/c，c为光速，rect(·)表示矩形窗函数，tr、Tp、tac与fc分别表示距离时间、脉冲宽度、波束中心扫过目标的时刻与中心载频，γ为信号调频率。

可以看出，实际的斜距历程是理想斜距与振动幅度投影至雷达视线方向的分量之和。利用传统成像方法对其直接进行处理后，会使振动误差相位项与距离产生耦合，由此产生的距离依赖振动误差相位不仅会对图像质量造成影响，而且也无法通过自聚焦方法对其进行估计补偿。因此，如何获得非距离依赖的振动误差相位是进行ROSAR振动误差补偿的关键。

2 ROSAR振动相位误差补偿算法

由上文可知，为能够利用自聚焦算法消除平台振动所引起的图像散焦问题，非距离依赖的振动相位误差是必不可少的。在本节中，我们提出了一种新的ROSAR成像算法来获取非距离依赖的误差相位，并结合WML-PGA对其进行估计补偿，进而改善ROSAR图像质量。

2.1 基于双重多普勒Keystone变换的ROSAR成像算法

对式(5)沿距离维做傅里叶变换并做距离脉压后，信号改写为

(6)

其中fr表示距离频率，Br为信号带宽，且有Br=Tpγ。将振动模型η代入信号回波表达式中，并将其各次谐波的正弦调制项按照贝塞尔级数形式展开，式(6)可改写为

(7)

其中，Jn(·)表示n阶贝塞尔函数，且有

h=4πAkcosα(fr+fc)/c

(8)

考虑到ROSAR的理想斜距是包含有余弦函数的复杂表达式，为简便起见，这里将理想斜距Ri(ta)在点ta-tp=0处，按照泰勒级数展开至二阶得到

Ri(ta)=R0+k1(ta-tp)2

(9)

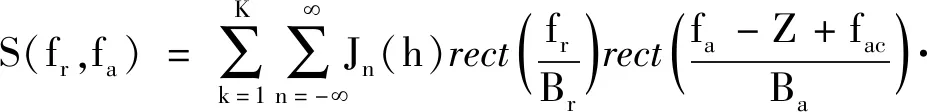
(10)

其中Z=n·Nk/Tk，fac表示波束中心扫过目标时刻所对应的的方位频率，Ba与Ka分别表示多普勒带宽与多普勒调频率。这里我们利用DDKT方法对距离徙动进行校正，关于单次DKT的详细介绍可以参见文献[14]。本文中所使用的Keystone变换核为

(11)

对式(10)做第一次DKT变换后，回波的二维频谱可以改写为

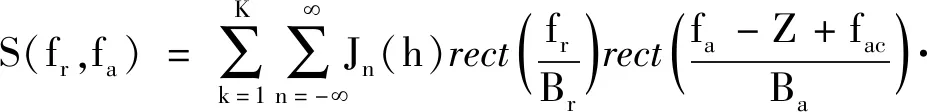
(12)

G(tr)表示对信号沿距离维做逆傅里叶变换后关于距离时间的相位项，且有

(13)

构造补偿函数Haz_q=exp{jπfa2/Ka}，在距离-多普勒域内对式(12)中的二次项进行补偿后，再次将信号变换至二维频域，并对信号做第二次DKT处理，可推导得到变换后的信号形式为

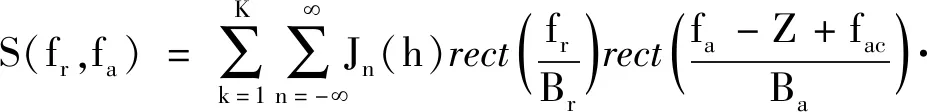
(14)

随后将式(14)变换至距离-多普勒域

(15)

式(15)中倒数第二项为剩余视频相位项，需要对其进行补偿，但是由于其中Z的数值未知，无法直接构建补偿函数将其消除，需要考虑其他方式将其补偿。将式(15)沿方位向做逆傅里叶变换至二维时域得到

(16)

(17)

式(17)给出了ROSAR信号包含振动误差在距离-多普勒域内的解析表达式。可以看出经过所提算法处理后的振动误差不再与距离耦合，这也意味着每个距离单元内的相位误差是一致的，振动误差不再依赖于距离，这一点也满足了使用自聚焦算法的先决条件。

2.2 基于加权最大似然相位梯度估计的振动相位误差补偿方法

在利用上一节中所提的方法对ROSAR回波信号进行处理后，即可得到非距离依赖的振动相位误差项，再结合现有的自聚焦处理算法即可实现对其的精确估计补偿。考虑到高信杂比的距离单元样本会提升振动误差的估计精度，这里我们利用加权最大似然相位梯度算法来改善ROSAR图像的聚焦性能[15-16]。WML-PGA算法的处理流程如下：

第一步：提取待估计样本，为增大估计样本的多样性进而提升误差估计精度，可以考虑从距离-方位两维进行筛选；

第二步：将强散射点按照圆位移的方式搬移至数据中心，以此来消除线性项的影响；

第三步：对样本进行加窗处理，进一步抑制旁瓣杂波的影响并提升改善待估计样本的信杂比，窗长的选择可以利用自适应方式进行计算，也可以通过手动选择窗长，同样可以得到较好的效果；

第四步：利用加权最大似然估计算子对样本的相位梯度进行估计

(18)

其中wm为第m个距离单元所加权值，该权值的计算方式为

wm=([Amean(m)]2+Avar(m))/Avar(m)

(19)

Avar(m)与Amean(m)分别表示所选择距离单元幅度的方差与均值，具体计算方式为式(20)。

(20)

在实际中，随着迭代次数的增加，滤波窗长可以设计为逐步减短以提升滤波效率。式(18)中的加权处理能够突出高SCR样本在估计中的作用，同时抑制低SCR样本的影响。这一处理也能够有效降低估计样本数量的要求，并加快整个算法的迭代收敛速度，经过上述方法处理后，系统振动误差相位即可得到较为精确的估计与补偿。将补偿后的信号沿方位逆傅里叶变换后，即可得到聚焦后的ROSAR信号时域表达式为

(21)

需要注意的是，利用WML-PGA估计得到精确的相位误差的前提，是式(17)中获得的非距离依赖振动误差相位项，在后面的仿真实验部分会再次对这一结论进行验证。

所提方法的处理流程图如图2所示。

图2 所提算法处理流程框图

3 仿真实验与实测数据处理结果

在本节中，选用BO 105型直升机作为实验平台，ROSAR系统参数在表1中给出。由于ROSAR的合成孔径时间通常较短，因此认为在一个完整的合成孔径时间内的谐振次数为2次即可较为合理地描述振动误差的运动特性。第一次谐振与第二次谐振的周期与幅度分别为0.45s，0.18g与0.89s，0.1g。

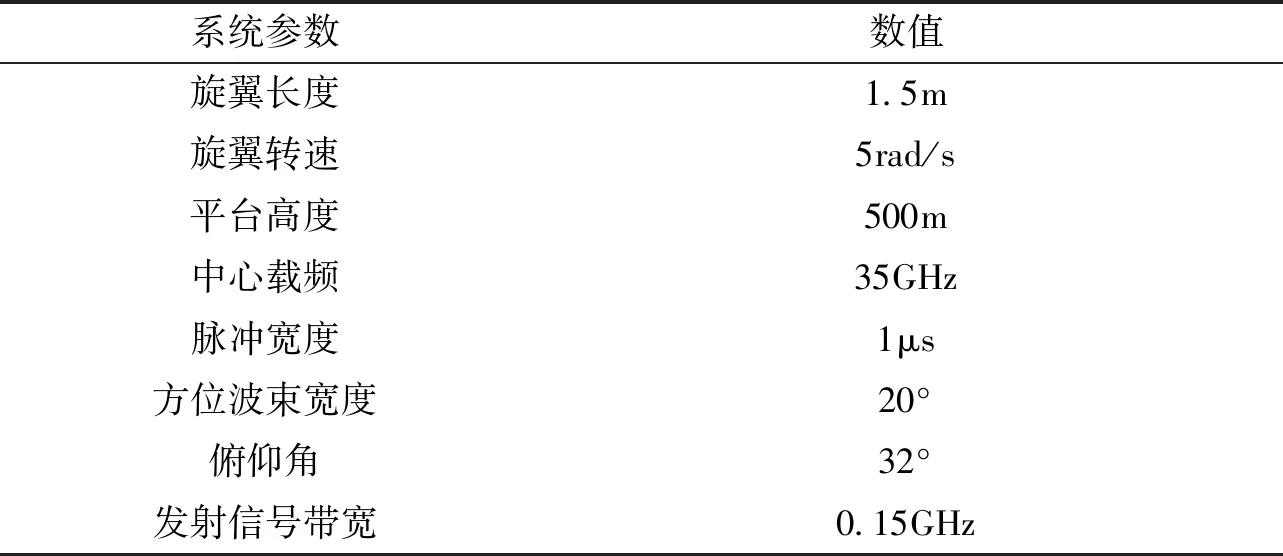
表1 仿真实验系统参数

仿真实验在场景中心附近设置九个目标点，且每组相邻目标点在角度维与距离维上的间隔分别为25°与45m。图3(a)与图3(b)分别给出了利用所提方法与传统的RD算法处理后得到的成像结果。由图3(a)可以看出，经过所提算法处理后，各目标的相位误差空变性已经被消除，具有非距离依赖性与一致性，再利用WML-PGA对其进行估计后即可获得精确的误差相位，补偿后即可得到聚焦效果良好的ROSAR成像结果。而图3(b)中，由传统算法处理后的成像结果可以看出相位误差仍具有较强的空变性，结合自聚焦算法估计后，仅有局部的目标点实现了聚焦，场景中的大部分点目标仍然存在严重散焦。由此可以初步证明所提方法能够有效消除运动误差空变性并对其进行较为精确的估计补偿。

为进一步对成像性能进行分析，在图3(a)与图(b)中分别选取目标点A与B进行分析，放大后的成像点目标结果如图4(a)与图5(a)所示。考虑到目标点在距离向经过精确脉压后即可获得良好的距离像，这里我们简单将其相应的性能参数在表2中给出后，便不再对其进行详细讨论，主要对角度维成像性能进行分析。选取相应的目标点沿距离向做切片后获得对应的角度维脉冲响应函数进行分析，这里主要利用峰值旁瓣比(PSLR)与积分旁瓣比(ISLR)两项指标进行分析，给出积分旁瓣比的计算公式为式(22)。

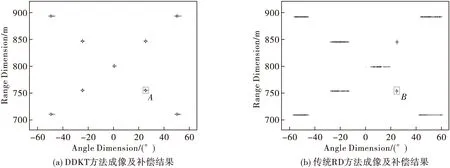
图3 所提算法与传统算法仿真场景成像结果

图4 点A成像性能分析

图5 点B成像性能分析

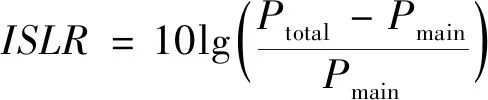
(22)

其中Ptotal与Pmain分别代表脉冲响应函数的信号总功率与主瓣功率，考虑到相邻两个目标旁瓣之间会相互累加进而对积分旁瓣比的计算产生影响，因此在计算积分旁瓣比时选取的总采样点数不宜过多，这里我们选取以主瓣为中心总长度为400的角度维采样点数来计算相应的积分旁瓣比，相应的结果在表2中给出。由表2可以看出，点A与B的峰值旁瓣比较为接近，但点A的积分旁瓣比与理论值相比的损失明显较小，可以证明所提算法成像结果更优，除此之外，所提算法对场景中所有目标点均能实现较好聚焦，而传统算法处理后的场景回波由于存在空变性，仅有特定角度上的目标点能够实现聚焦，其余目标点均存在较为严重的散焦现象，上述仿真结果验证了所提算法的有效性与优越性。

表2 点目标A与B成像性能参数表

图6给出了两种算法估计得到的振动相位误差与实际添加振动误差的偏差值，并统计计算了两种方法估计偏差的最小均方值，可以看出所提算法对运动误差的估计偏差值接近于0，即与真实误差接近，而传统算法的估计偏差始终较大，无法得到误差的精确估计值。

图6 两种方法估计振动误差相位与真实值的相位差

最后我们利用仿真实测场景对两种算法进行验证对比，在仿真实测数据中添加与此前仿真参数相同的正弦振动误差，图7(a)与图7(b)分别给出了成像后与自聚焦处理后的成像结果。由图像可以看出传统方法处理后的图像仍然存在较为明显的散焦现象，而所提方法处理后的图像中，整个场景都得到了较好的聚焦。对两幅图像的熵值进行计算，可知图7(a)与图7(b)的熵值分别为13.99与13.69，这一结果再次验证了所提算法的有效性。

图7 仿真实测场景数据处理结果

4 结束语

本文提出了一种基于双重多普勒Keystone变换的ROSAR成像与振动误差补偿算法，利用贝塞尔级数对含振动误差的ROSAR回波信号进行展开推导，并利用双重多普勒变换(DDKT)有效地校正了由平台振动误差与斜距历程变化所引入的距离徙动，在推导补偿了视频剩余相位后得到了非距离依赖的、具有一致性的误差相位项。结合加权最大似然相位梯度自聚焦算法即可估计得到准确的相位误差，利用估计得到的运动误差对回波信号进行补偿后即可获得聚焦效果良好的ROSAR图像。最后通过仿真实验验证了所提算法的有效性与正确性。