一种无人机辐射源调制样式识别算法 *

黄祥,徐静,都晨,郭昭艺,吴涛

(江苏方天电力技术有限公司，江苏 南京 211102)

0 引言

近年来，低空空域的开放使得无人机市场规模迅速扩大，因而民用和商用无人机在诸多领域备受青睐，如无人机送快递、无人机巡线等。无人机的广泛应用为日常生活带来便利，但同时也因其低慢小的特点为低空空域安全带来隐患[1]。在电力领域，大中型变电站、重要输电线路等电力基础设施均面临无人机造成的低空安全风险问题。因此急需研究适用于电网应用场合需求的低空安防系统。针对无人机安防系统的重要功能是对无人机的有效识别，由于无人机需要通过遥控方式进行破坏行动，因此可通过对无人机操控信号开展侦察识别研究。

小型商用和民用无人机通常使用直接序列扩频(direct sequence spread spectrum,DSSS)信号进行操控，而DSSS信号的功率谱密度较低，如何实现低信噪比条件下DSSS信号的高效识别成为无人机侦察领域亟待解决的重难点问题。

目前，通信信号调制样式识别的主流方法有基于判决理论的识别和基于特征的识别[2]。基于判决理论的识别方法又称为似然比检验(likelihood ratio test,LRT)方法，文献[3]利用统计特征进行信号识别，但其识别率较低且对低信噪比环境适应性较差[4]。基于特征的识别方法一般包含特征提取与分类识别2部分，其中特征提取部分通过各类变换方法获取信号的多级特征，灵活性较高；分类识别部分多采用分类算法完成识别；此外，深度学习等算法也可通过数据学习同时完成特征提取与分类识别。目前，针对DSSS信号的识别研究已有部分成果，文献[5]提取循环平稳特征完成MPSK-DS信号识别；文献[6]提取信号四阶累积量特征完成DSSS信号识别；文献[7]利用Wigner-Ville时频分析方法提取无人机测控信号时频域特征，并使用BP神经网络进行分类识别；文献[8]从功率-频率图中提取幅度相位信息，利用五层卷积神经网络(convolutional neural network,CNN)对802.x标准下的WIFI，Bluetooth，ZigBee及其混合信号进行分类识别；文献[9-10]采集了大疆精灵4型无人机实测信号，并提取其时域和频域特征，利用人工神经网络进行识别。

上述文献虽用到了特征提取与神经网络的方法，但均未考虑CNN对图像结构特征卓越的识别能力。针对上述情况，本文提出一种基于CNN的DSSS信号识别算法。首先，该方法通过短时傅里叶变换(short-time Fourier transform，STFT)将一维时域信号转换为二维时频域图像；其次，提出了能量阈值降噪方法进行时频图降噪，并采用临近差值法进行图像降维以降低运算量；最后，设计了CNN用于分类识别，仿真验证了方法的有效性。

1 基于能量阈值降噪的时频预处理

1.1 信号模型及时频分析

DSSS信号是一种大带宽、低功率谱密度的非平稳信号，一般采用BPSK作为脉内相位调制方式。在高斯白噪声背景下，信号模型为

s(t)=x(t)+n(t)，

(1)

式中：n(t)为噪声，x(t)和s(t)分别为发送端信号和接收端信号。

一维时域信号稳定性较差，时频变换能够形成更为稳定的特征。STFT为经典时频变换方法，给定一个时间宽度很短的窗函数w(t)，则信号s(t)的STFT定义为

(2)

STFT是时间和频率的二维函数，一维时域信号经短时傅里叶变换后可形成二维时频图，其具有良好的结构特征，可供CNN学习。

1.2 能量阈值降噪方法

噪声对信号结构造成不同程度的干扰，图1所示为-5 dB条件下DSSS信号时频图。噪声成分影响最终识别效果，为改善时频图质量，降噪处理十分必要。

图1 -5 dB时的DSSS信号时频图Fig.1 Time-frequency distribution of DSSS signals at -5 dB

文献[11]采用随机投影(random projection,RP)和主成分分析法(principal component analysis,PCA)进行降噪，该算法提取时频图中信号主要能量，但去除噪声分量的同时也破坏了时频图的结构特征，不利于CNN学习；文献[12]利用6次零均值归一化算法进行降噪，但未考虑到能量因素，降噪过程中易将很多高能量的信号点当作噪声滤除。

因此提出能量阈值降噪法，旨在保留信号时频结构特征与主要能量。假设经STFT所得时频图为，则能量阈值降噪法定义如下：

(3)

式中：|Ii,j|表示时频图中每个像素点的能量值；η为阈值门限系数。目前客观图像质量评价指标主要有峰值信噪比(peak signal to noise ratio,PSNR)、结构相似度(structural sIMilarity,SSIM)及特征相似度(feature SIMilarity,FSIM)[12]，主要考虑图像结构特征，故选择SSIM作为评价指标。该指标由3种对比模块组成，分别为亮度、对比度和结构。x,y是2张图像，SSIM指标的定义如下

SSIM(x,y)=[l(x，y)]α·[c(x,y)]β·
[s(x,y)]γ,

(4)

式中：α,β,γ>0，用来调整3个模块之间的重要性，通常取1；l(x,y),c(x,y),s(x,y)与x,y的均值、标准差和互协方差有关。

(5)

(6)

(7)

式中：μx,μy,σx,σy和σxy分别为图像x,y的均值、标准差和互协方差，为简化公式，通常设α=β=γ=1,C3=C2/2，式(4)简化为

(8)

SSIM的取值范围在0～1，SSIM值越接近1表示降噪效果越好，和原图像具有越好的结构相似度。为了找到合适的阈值门限η值，设计如下对比实验。在信噪比为-10 dB和10 dB时，设置门限分别为1/5，1/4，1/3，2/5和1/2计算SSIM值，实验结果如表1所示。

表1 不同门限下SSIM值比较Table 1 Comparison of SSIM values under different thresholds

从表中可以看出，门限选择1/3时，SSIM值较高，降噪后的图与高信噪比下的图具有更高的结构相似度，故门限选择为1/3。

1.3 图像降维与归一化

为提高识别效率，对降噪处理后的时频图进行降维处理。使用等间隔采样法对高维时频图进行降维，降维前的时频数据大小为512×512，降维后的时频图数据大小为64×64，如图2所示。横坐标为时间索引，纵坐标为频率索引[13]。

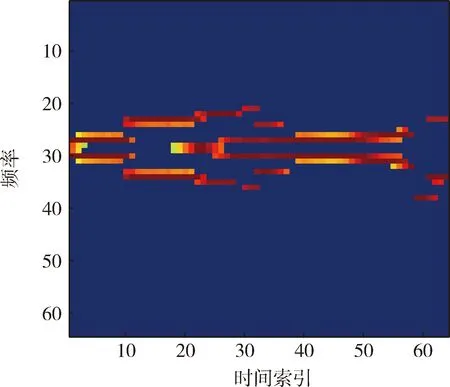
图2 降维后时频图Fig.2 Time-frequency diagram after dimensionality reduction

此外，时频图中的数值存在较大差异性，针对量纲不一致问题可以采用标准化区间缩放法将不用规格的数据转换到同一规格。本文采用区间缩放法，为便于计算，将时频图矩阵变为向量化表示，记作α=(α1,α2,…,αi,…,αm)，对每一个列向量αi做区间缩放，如式(9)：

(9)

式中：max(·)与min(·)分别为取向量的最大值和最小值。

2 基于CNN的分类识别

2.1 CNN及其训练

卷积神经网络主要由输入层、卷积层、池化层、全连接层和输出层构成。经信号预处理后的时频图记为X，n张时频图同时输入网络，wij表示时频图X与神经元连接的权重值，bj表示神经元内部状态的偏置值，yj为神经元的输出。则输入和输出之间的关系为

(10)

式中：*表示卷积；pool(·)为池化层函数，常用池化方法有最大池化和均值池化；σ(·)为激活函数，用于解决梯度消失和梯度爆炸问题，常用激活函数包括整流线性激活函数(rectified linear unit,ReLU),sigmoid函数和tanh(x)函数等。

选用ReLU和最大池化函数进行处理，经过多个卷积层和池化层提取特征后，全连接层用于整合卷积层或者池化层中具有类别区分的局部信息[14]。最后一层全连接层的输出值被传递给输出层，采用softmax层进行分类，最终输出各类概率表示为

(11)

式中：Sj为每类输出的概率，最大概率类判定为最终识别结果。

CNN的训练终止条件有2种，即迭代次数达到预设值或者损失函数值不再减小，此时认为模型收敛，并根据结果给出识别率。

2.2 算法流程

综上所述，给出图3所示本文算法流程图。训练信号和待识别信号首先进行相同预处理，即短时傅里叶变换、能量阈值降噪、图像降维及归一化处理，并输出训练集和测试集；随后将训练集送入CNN进行网络训练与优化，当迭代次数或者损失函数值不再降低时，则CNN训练完毕；测试集输入网络后输出分类识别结果。

图3 算法流程图Fig.3 Algorithm flowchart

3 仿真与分析

3.1 信号及参数设置

为验证本文识别算法的有效性，利用2种不同扩频方式下BPSK调制的DSSS信号进行仿真实验：①通过改变扩频码长度即扩频因子来实现扩频；②为固定扩频码长度，通过改变符号率来改变等效带宽实现扩频。2种方式下扩频码均采用m序列，具体参数设置如下：

(1) 第1种扩频方式采用长度为15，31和63的m序列，本原多项式分别如式(12)，(13)和(14)所示：

y=x4+x1+1，

(12)

y=x5+x2+1，

(13)

y=x6+x4+x3+x1+1.

(14)

信息码长度为10，采用随机生成方式；扩频码元速率为20 Mbit/s，由此生成的3种直接序列扩频信号记为DS1,DS2和DS3。

(2) 第2种扩频方式下固定扩频码选择长度为63的m序列，本原多项式为式(14)。现代无人机除通信任务外，还有对720 P,1 080 P和4 K高清视频传输需求，为适应无人机不同信息传输需求[15]，设置不同码元速率，即10 MHz/s,30 MHz/s，60 MHz/s；信息码长度均为10且随机生成。由此产生的直接序列扩频信号记为DS4,DS5和DS6。

以上6种信号每种产生1 000个样本；信号中混入加性高斯白噪声，信噪比范围为-10 dB～2 dB(步进2 dB)。STFT采用长度为N/4的Hamming窗，为信号长度。信号的产生和预处理采用R2015b版的Matlab，CNN利用TensorFlow搭建，计算机配置为CPU i5-4200U，GPU为NVIDIA GTX 1080Ti，内存为4.00 GB。

3.2 模型评价指标

在机器学习任务中，F1值(F1-score)是评价系统性能的常用指标，其为查准率(precision)和查全率(recall)的调和平均数，其定义为

(15)

式中：P为机器学习中的查准率，表示为：真正例/(真正例+假正例)；R为机器学习中的查准率，表示为：真正例/(真正例+真反例)；F1值多用来评价二分类任务性能。对于多任务，利用宏平均(marco-averaging)作为模型评价指标，即

(16)

(17)

(18)

式中：n为类别总数，式(16)，(17)分别用于计算查准率平均值和召回率平均值。式(18)用于计算宏平均值，此指标相对于传统评估准确率(accuracy)更具准确性，能够给出综合评估值。

平均时间作为算法复杂度的衡量指标，用于计算特征提取和训练识别的时间总和，其表示为

Ttotal=Tfeature+Ttrain.

(19)

3.3 仿真实验

CNN性能受超参数影响，网络层数是关键超参数之一，为确定合适的网络层数，设置2层、3层和4层网络分别进行实验。本实验采用高信噪比信号用于网络训练，低信噪比信号测试[16]。其目的在于低信噪比数据集信号结构受噪声影响，利用高信噪比信号完成网络训练，可验证本文所提能量阈值降噪法的降噪有效性；此外，该方式能够有效降低系统对训练数据集的标注需求。

CNN的卷积核大小均为3×3，步长为1；池化层采用大小为2×2，步长为2的最大池化函数。此外，各层保持不同的特征图(feature map)数量，2层CNN对应32和64；3层CNN对应32，64和128；4层 CNN对应64，32，12和8。CNN的优化采用学习率自适应的Adam函数，学习率α=0.001，矩估计的指数衰减率β1和β2分别为0.9和0.999，用于数值稳定的小常数ξ=1×10-8。为防止网络过拟合，训练网络中采用keep_prob=0.5的dropout正则化，即随机失活50%的神经元；激活函数采用ReLU；训练80个epoch。数据集的随机划分采用Sklearn库中的train_test_split函数，训练集和测试集按照 7.5 ∶2.5 比例划分。

实验结果如图4所示。实验结果表明：3层CNN结构识别结果最佳；虽然CNN层数越多对特征提取的能力越强，但网络优化需兼顾数据量等背景。选取3层CNN结构进行后续实验，图5为信号在-10 dB条件下识别的混淆矩阵。其中，DS3与DS6均为宽带信号，其功率谱密度较低，因而在低信噪比条件下的识别率相对更低。

图4 不同层数CNN识别结果对比Fig.4 Comparison of convolutional neural network with different layers

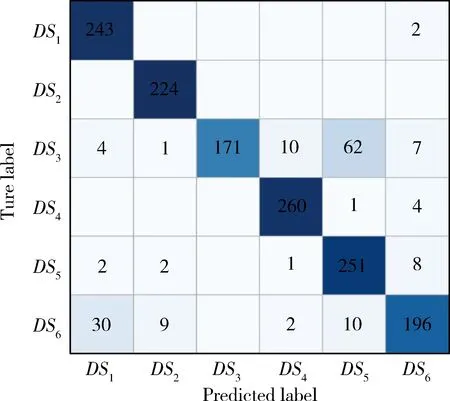
图5 -10 dB下的混淆矩阵Fig.5 Confusion matrix at -10 dB

3.4 算法对比分析

为验证本文识别算法的有效性，选择已有经典方法进行对比。文献[17]采用STFT变换获取时频图，并提取图像的方向梯度直方图特征(histogram of oriented gridients,HOG)与局部二值模式特征(local binary patterns,LBP)特征，融合后经PCA实现降维，再采用SVM进行分类，并结合KNN分类器进行对比；文献[7]利用BP神经网络对DSSS信号进行分类；文献[18]提出利用4层CNN与STFT时频图结合进行信号分类，对比实验结果如图6所示。

图6对比结果表明：文献[7]方法未进行降噪等预处理，其在低信噪比条件下的识别效果不佳；文献[17]所采用的HOG与LBP联合特征稳定性一般，即使在高信噪比条件下识别结果也难达到1。文献[18]利用高斯滤波器进行图像降噪，但在低信噪比条件下效果不及本文方法。

图6 各算法识别结果对比Fig.6 Comparison of algorithm identification results

为进一步对比计算复杂度，给出图7所示各算法识别所用平均时间。其中，特征提取用时为每种信号产生50个样本并完成特征提取的时间；训练识别为运行80个epoch的时耗。综合对比图6，7结果，虽然常规特征提取耗时短，但稳定性不佳；本文算法需一定时耗完成特征提取与训练识别，但具有较好的鲁棒性，在低信噪比条件下具备较高的识别率；此外，降噪处理能够一定程度缓解对低信噪比数据集的标注需求。

图7 各算法时间对比Fig.7 Time comparison of algorithms

4 结束语

在无人机应用背景下，提出了一种新型基于CNN的辐射源信号调制样式识别算法。算法利用短时傅里叶变换、能量阈值降噪等获取预处理时频图，随后送入CNN进行特征映射与分类识别。在信号预处理环节，提出的能量阈值降噪法能够有效抑制噪声干扰，信噪比为-6 dB时的识别率达到0.97。与传统特征及其他识别方法相比，识别率更高且低信噪比环境适应性更强。