培养“数学抽象”素养，设计“有思维的教学”

2021-07-20过晓伟

数学学习与研究 2021年17期

过晓伟

【摘要】数学抽象是数学特性之一，它可以让学生积累从具体到抽象的活动经验，更好地理解数学概念、方法、体系，养成一般性思考问题的习惯，能主动地用数学抽象的思维方式去解决问题.小学阶段则更多通过抽象概括、符号应用和模型思想来培养数学素养，为今后数学抽象打下基础.

【关键词】核心素养;数学抽象;数学思维

抽象是数学的特性之一，是指舍去事物的一切物理属性，得到数学研究对象的思维过程.可以讲，没有抽象就没有数学的研究对象，数学的推理和应用都离不开抽象.小学阶段的数学抽象，更多表现为概括、推理、符号应用和模型建立.如果我们能把握住学生学习的规律和数学抽象的本质特点，加强培养学生的抽象能力，就能让学生理解数学知识之间的层次性和结构规律，促进学生的思维发展.以下以苏教版小学三年级上册“长方形面积计算”为例，谈一谈数学抽象在小学阶段的渗透与应用.

一、经历过程，由繁至简，发挥表象作用

经历是数学活动的过程性目标，让学生亲身经历知识、技能形成过程，能更好地培养学生的数学素养.几何形体在生活中比较常见，但是对于几何形体的内在认识，学生由于思维特点和实践经验的不足，不能对相关知识进行清晰全面的了解.因此，学生在数学学习中参与观察、操作、比较、概括等形象的实践活动，特别是经历知识概念的抽象过程，就能厘清知识的内在的联系，为进一步抽象提供基础，同时能架起由具体感知到抽象思维的桥梁.

【片段1】

用“面积单位”直接度量长方形的面积

谈话：给你一些1平方厘米的小正方形，你能想办法量出长方形的面积吗？看谁想的办法最巧妙.

学生操作，教师巡视.

交流：你量得的面积是多少？你是怎么看出来的？

预设：（1）满铺量.（2）半铺量.（3）简铺量.

小结：像这样量一量，我们就能知道每排摆4个，摆了这样的3排.一共有12个1平方厘米的小正方形，面积就是12平方厘米.

（4）一个面积单位度量.

引导：如果只用1个小正方形，你还能量出它的面积吗？（见图1、图2）

指出：用1个小正方形量也能知道每排能摆几个1平方厘米，能摆几排，就能知道一共有多少个1平方厘米，也就知道了长方形的面积.

教师让学生在丰富的实例中经历学习过程，便于帮助学生获得充分的感知，为抽象提供帮助.以上的实践操作中，学生经历了用多个面积单位到用1个面积单位度量的过程，在脑中建立了12个面积单位满铺的表象，获得了“数—算”的经验.学生在经历多个小正方形的铺设的过程中，通过观察逐渐获得小正方形数量总数就等于长方形的面积，脑中也建立了“求长方形的面积就是求出小正方形的个数即可”的想法.接着又经历了只用1个面积单位度量的过程，又对度量的数量计算方法进行由繁到简的自我优化，经历了过程，发展了思维，为接下来的实物抽取过程打下基础.几何概念的学习，经历有思维的学习过程十分重要，只有让学生在观察、分析、思考中留下深刻的印象，问题才会在进一步抽取共性知识的过程中迎刃而解.

二、把握时机，由表及里，适时抽象概括

学生经历了丰富的实践活动，已经获得了一定的感性认识，但他们只是通过原有经验与表面观察获得的感性认识，还是比较粗糙和肤浅的.教师可以适时进行理性思维引导，由表及里，去粗存精，引导学生从中选取某种本质属性，加工、提炼，这种过程就是抽象概括的过程.抽象概括的过程，实际上就是把感性认识上升到理性认识的过程.

【片段2】

用“尺”间接计量长方形的面积

引导：如果一个小正方形都没有，你还能知道每排摆几个，摆几排吗？

（1）出示长方形，追问：你怎么知道一共摆了多少个1平方厘米的小正方形呢？

（2）长方形变化：现在长方形的面积是多少呢？说出思考过程.

（3）长方形继续变化：现在，长方形的面积是多少？

（4）再变：长方形的面积是多少？

（5）谈话：接着变，还能再变吗？长方形的面积要怎样求？（板书：长×宽）（见图3、图4）

史宁中教授认为，抽象可以在感性具体与理性具体之间搭建思维的桥梁.以上教师首先通过“如果一个小正方形都没有，你还能知道每排摆几个，摆几排吗？”这个核心问题及连续几个变化的问题，让学生反思先前的操作过程，特别是计算小正方形的方法，引发“每排几个，摆几排”与长方形的长与宽之间的关系，通过讨论，学生能概括出“每排几个”等同于“长”的长度，“摆几排”等同于“宽”的长度，由此螺旋上升為计算长方形的面积不再需要摆和数小正方形了，只要丈量长与宽的长度，计算便知.在这充满思维的情境中，适时进行概括，不仅让学生经历了长方形的大小变化与尺子刻度之间存在的内在关系，而且能让学生在对具体图形中充分感知，形成表象后，及时地进行概括，学生很快便能抽取出长方形面积计算的方法和条件.充分感知，把握时机，及时抽象，能使学生的感性认识上升到理性认识，提高学生的思维能力.

三、感悟层次，由浅入深，建立数学模型

数学抽象能力不仅能使学生厘清各数学因素之间的相互联系、核心和本质，还能培养学生把具体问题抽象成数学模型的能力.对于深度思维的培养，学生需要经历数学知识产生的过程，体会数学知识之间的层次性和结构规律，教师还需要让学生找到数学概念的原型，感受到数学知识本身的形式化、模式化的特点，逐步建立初步的“模型思想”.

【片段3】

概括提炼，生发计算公式

小结：看来，不管长方形怎么变，知道了长，就知道每排能摆几个面积单位，知道了宽，就知道了能摆几排，用长乘宽就能算出长方形中包含了多少个面积单位，长方形的面积就是多少.这就是长方形的面积计算公式.（板书：长方形的面积=长×宽）.

如果用a表示它的长，用b表示它的宽，S表示长方形的面积，这个公式还能写成S=ab.（板书：S=ab）

皮亚诺指出：“数学中的一切进步都是引入符号后的反响.”数学其实就是一个符号化、形式化的系统.以上丰富的操作活动与具有思维性的数学活动让学生对长方形的面积计算方法逐步清晰起来，他们已能用语言描述面积的计算方法.教师相机引入字母，学生便顺理成章地获得了长方形面积字母计算公式其实是一个能描述长方形面积与长、宽之间内在联系的数学结构表达式.这个用符号建立的表达式不仅能表达数学问题的数量关系和变化规律，而且它将现实的数学问题简化、抽象为形式化的符号表达，简明易记.教师通过此公式的得出过程进一步培养了学生的抽象思维能力.

四、应时变式，由此及彼，提升数学思维

丰富的抽象过程能提高学生的抽象能力，而形式多样的变化习题更能培养学生去伪存真、捕捉共同特征的抽象素养.利用抽象方法做的数学设计，学生在初步了解概念、计算公式后，还需要由此及彼、由表及里地深化，适时运用变式练习从不同的角度或以不同的方式去进一步认识新学知识的本质属性.在这一过程中，学生通过探索、交流、发现，在与新知识的比较、分析中，逐步形成了新的知识结构与体系.

【片段4】

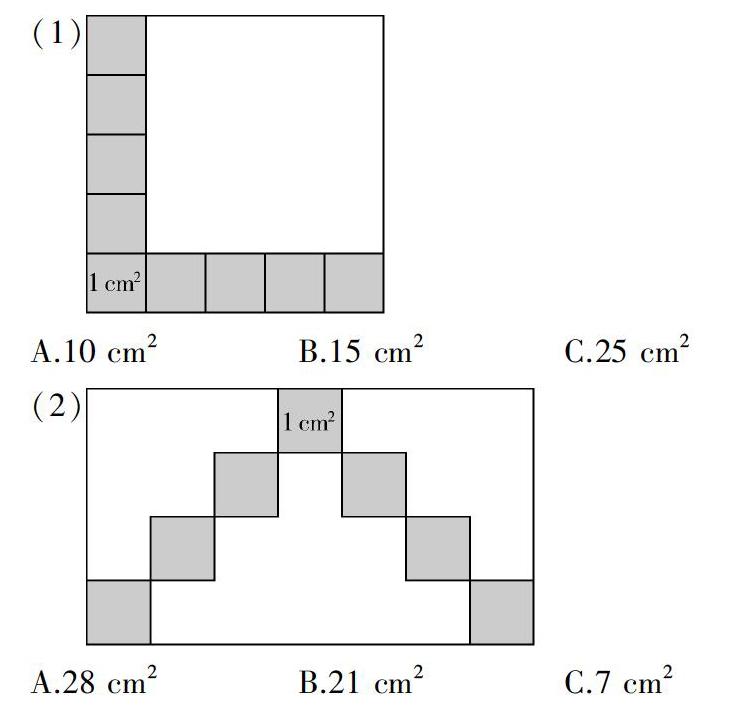
选一选

图中每个小正方形表示1 cm2，图形的面积是（）.

辨一辨

出示题目：有一块长方形草坪，长50米，宽20米.

（1）这块草坪的面积是多少平方米？

（2）小明沿着草坪的四周走了一圈，他走了多少米？

变一变

（1）设计一个面积是18平方厘米的长方形.

（2）如果把长方形的长和宽同时乘2，长方形的面积会发生怎样的变化呢？

以上教师设计了三组（条件变化、面积與周长、等积异形）变式题组，学生抽象思考与讨论探究，教师引导、点拨，学生从而梳理例子中的异同，提取概念的本质属性，不仅掌握了解决这一类问题的方法，获得整体认识，而且透过了现象弄清了这类问题的本质，对所学内容得到更深层次的理解和认识.

数学抽象既是数学核心素养之一，又是基本的数学思想.教师在教学时，要精心设计数学知识逐步抽象概括的过程，使学生经历从具体到抽象，又从抽象到具体，由直观现实化抽象到概括化的发展过程，引导学生进一步构建抽象思维，形成抽象思维系统，最终实现抽象思维与具象层次的转化.