基于儿童数学活动经验积累的教学实践与思考

张云燕

【摘要】《义务教育数学课程标准（2011年版）》总目标的第一条，从原来的“双基”扩展到“四基”，其中增加的就有基本活动经验，基本活动经验和儿童新知的生长和建构密切相关，教师要设计有效的数学活动，让学生在动手操作中积累经验，在参与游戏中总结经验，在画图表征中发展经验，在观察对比中提炼经验，在回归生活中应用经验.

【关键词】小学数学;活动经验;儿童;思维

《义务教育数学课程标准（2011年版）》在总目标的第一条明确指出：“通过义务教育阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验.”这一目标简称“四基”，与实验版的课标相比，增加了“基本思想、基本活动经验”，由此可见帮助学生积累基本活动经验的重要.

所谓基本活动经验，是指学生通过亲身经历数学活动的过程，从而获得具有个性特征的经验，数学活动经验不仅是指数学实践活动的经验，更重要的是指数学思维活动的经验.史宁中教授认为：“基本思想和基本活动经验是一种隐性的东西，恰恰是这种隐性的东西体现了数学素养.”也就是说，帮助学生积累基本活动经验，就是在培养学生的数学核心素养.本文以一年级数学教学为例，谈一谈基于儿童数学活动经验积累的教学实践与思考.

一、在动手操作中积累经验

皮亞杰认为，在个体从出生到成熟的发展过程中，认知结构在与环境的相互作用中不断重构，从而表现出具有不同性质的不同阶段，他将儿童和青少年的认知发展划分为四个阶段：感知运动阶段、前运算阶段、具体运算阶段和形式运算阶段.一年级的孩子处于前运算阶段，皮亚杰把这一阶段又划分为两个阶段：前概念或象征思维阶段和直觉思维阶段，也就是说一年级孩子的思维活动具有相对具体性，不能进行抽象运算思维，因此教师教学中需要大量直观的素材和具体的操作活动，让孩子的视觉、触觉、听觉等多感官参与.

一年级的教学内容绝大部分都是计算，“10以内和20以内的加减法”是整数加减法的重要基础，可以这样说，如果一年级的加减法没有打好扎实基础的话，那么以后所有的整数加减法就很难保证计算正确.那么，如何帮助学生打好这个基础，积累相关的经验呢？利用动手操作来帮助学生理解算理、掌握算法是一个重要而有效的策略.

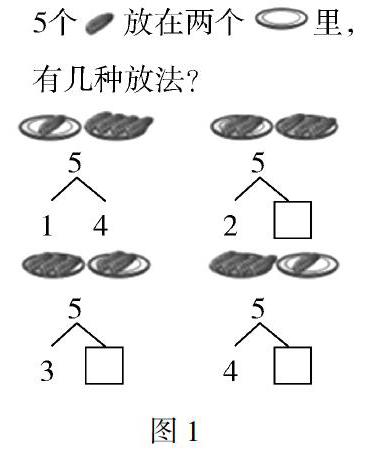
10以内的加减法以数的分解组成作为算理的基础，在教学1～5各数认识时，先让学生把物品分成两份，然后引导学生从无序到有序（如图1），在分物过程中积累数学活动经验，而这种经验，不仅仅只是操作学具的经验，更重要的是有序思维的经验.学生掌握了把数有序分解的方法，那么就可以迁移运用到后面6～10各数的认识中，就能很快地把数的所有分解组成有序地找出来，不重复也不遗漏.

又如，“20以内的进位加法”（图2），借助小棒的操作，凑十法的理解就更直观和深刻，而且这种经验具有良好的迁移性.只要理解了为什么要从4里面分出1，为什么是分4而不是分9，学生理解清楚了，就可以把经验迁移到9加其他的数，继而迁移到8，7，6，5加几的计算上.

当然操作活动不仅限于计算教学，在其他很多教学内容中也能充分发挥作用，有效帮助学生积累数学活动经验，如义务教育教科书人教版一年级下册第7页第8题（图3）：

8.折一折，用做一个，“4”的对面是“（  ）”.

这题对一年级学生来说，抽象地想或讲解根本无法理解，缺乏类似的经验积累.如果仅仅是教师利用实物进行演示性的讲解，或者利用课件动画展示，这些一晃而过的画面都不是学生自己的操作活动，无法获得自己的操作经验，因此，笔者要求学生把展开图做成正方体，要求在做的过程中先想象，其他数字所在的面在4这个面的什么位置，再折一折，验证想象;然后反过来，展开正方体各面，在展开前想象展开后的样子，再操作验证想象.在折围和展开的操作活动中不仅解决了问题，同时培养了空间观念.最后，教师出示图4，与教材图进行对比，从而引出：要找4对面的数字，首先要排除和它相邻的数字（图4），这样一来，就只剩“5”了，由此学生发现了其中蕴含的秘密，在操作活动中积累了新的经验.

二、善用画图发展经验

如前所述，一年级学生更多的是用直观思维来理解问题，因此遇到一些稍复杂或抽象的问题时，可以充分利用直观的手段来帮助学生理解，把抽象问题直观化、具体化，从而找到解决问题的方法.画图就是学生解决问题的一种很重要的策略，画图策略在理解概念、解决问题以及空间与图形等各个领域都有很大的优势.而这种策略的培养不是到了中高年级才开始的，从一年级就可以开始，如人教版一年级上册教学画图应用问题时，可以画这样的简图对加法和减法进行对比，帮助学生进一步理解加减法的意义，初步感受加与减之间的关系，明确什么时候用加法，什么时候用减法.

再如，人教版一年级上册第79页例6这类非常规或稍复杂的问题（图6，7，8）.

教师要放手让学生尝试用自己的方法解决，然后有所侧重地渗透画图的策略，让学生了解这种策略，初步积累画图解决问题的经验，然后在解决教材第80页的第5题时，就可以尝试迁移运用这种画图的经验了.

教材第80页的第5题：11月5日星期一，老师说“今天有雨，运动会推迟3天再开.”“推迟后，运动会星期几开？”

生：可以数一数，或者像昨天那样画一画.

教师给予表扬，学生尝试画图，如下：

生1：星期一 ○○○

生2：星期一 二三四

师：他把数字标在方框里，是不是更清楚？为什么你们都从星期二开始数？

生：5号是星期一，接着就是星期二.

最后在教师的引导下，学生对画图进行了改良，变成在“星期一”后面画横线填空的方式.讲解抽象难以理解的知识，通过画图，直观，简单，可行，由此也可以发展学生画图的经验.

三、在观察对比中提炼经验

一年级学生的认知水平虽然大多停留在直观层面，但并不意味着就不需要培养抽象概括的能力，事实上，小学阶段所要培养的思维，都可以在一年级开始就进行渗透和培养，学生各种经验积累的过程，是一個循序渐进、螺旋上升的进程，只要选用合适的教学策略，再简单的知识都可以为高阶思维的培养打好基础，积累相关的活动经验.

如人教版一年级上册“加法和减法的认识”，虽然教材没有给出加减法的定义，不需要教学概念，但是可以设计这样的观察对比的活动，让学生从中感悟加减法的意义.

把前面学习的几个情境放到同一页PPT上：

用问题“有什么相同的地方？”引导学生观察对比，逐步发现，虽然这三件事情不同，数量也不同，但是相同的是，都是把两部分合起来求得最后一共是多少，都用加法计算.经历这样的教学，学生虽然没有出加法的概念，但是加法的本质特点学生已经感悟到了，关键是学生经历这样的一个观察对比的过程，抽象概括能力就得到培养，也朦胧地感受到了透过不同的事情找相同的地方，并积累了开展这种观察对比活动的经验.

再如，“认识钟表”一课，教学的目标不仅仅是了解钟面的构成，学会看时间，这么简单感觉不用教的内容，其实也是学生积累观察对比、抽象概括经验的极好素材，可以安排这样的观察对比的活动：

教师引导学生观察对比：有什么相同的地方？由此抽象概括出传统钟面和电子钟面看整时刻的方法，进一步积累观察对比、抽象概括的经验.

四、在参与游戏中感悟经验

兴趣是最好的老师，教学设计再好，如果没有学生的积极参与，那么教学效果就会大打折扣.照本宣科的教学只会让学生感到枯燥乏味，尤其是对于自制力还比较弱的一年级学生来说，因此需要设计一些有趣的活动来调动学生的学习积极性，其中数学游戏就是一种很好的数学活动.

在一年级，“数的认识”是重点教学内容，其中基数与序数的含义学生是比较容易搞混的，是教学的难点之一，如何突破这个难点呢？笔者在“6和7的认识”的教学中，设计了趣味运动比赛项目，讲台前站着10名学生，其他学生要完成几个活动：

（1）要求给右数第6个同学送花;

（2）从左数起的6个同学蹲下;

（3）指挥从左数起的第7个同学唱队歌.

这样的数学游戏活动，让学生深刻理解了6作为基数和序数的含义，积累了数数的经验.

五、在回归生活中应用经验

学数学是为了用数学，在应用中进一步理解加深记忆.有研究成果表明，学习知识后马上应用，可以记住90%的内容.为了提升数学的趣味性，教师可以贴合生活，尽量设计有趣有效的应用.

一年级学生学习了人民币之后，由于学生年纪小，生活常识和经验都不够，对“付的钱数”“找的钱数”等没有概念.可以设计这样的应用练习：和家长一起去购买游玩活动需要的午餐食品，要根据购买情况填写登记表，花费在20元以内.

学生通过这次的购物活动，对“付出的钱-物品的价格=找回的钱”印象深刻，有了实践经验，知识掌握得特别牢固，这就是应用的“威力”.

教师从学生已有的经验出发，创设了高效的数学操作活动，契合学习的有趣游戏，简单又有助于理解的画一画活动，以及现实生活中的实际应用等数学活动，学生在这些数学活动中，动手、动口又动脑，多种的感官被调动，参与数学的学习活动，真正获得了新的知识.

【参考文献】

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2]史宁中.基本概念与运算法则[M].北京：高等教育出版社，2013.