基于单向拉伸仿真对各向异性薄板本构修正的研究
2021-07-20张东凯李晓广余亚克
张东凯,李晓广,余亚克
(河钢集团邯钢技术中心,河北 邯郸 056038)
传统板料冲压成形主要依靠设计者的经验,即通过不断修模、试模、调整间距及压边力等试错方式,来解决成形中出现起皱、破裂等问题。随着汽车工业的发展,板料冲压成形工艺趋于复杂,传统方法导致零件生产周期长、效率低,已经不能适应成形工艺的发展。而计算机技术和有限元方法的发展给板料成形带来了新方法,通过计算机仿真模拟冲压工艺、指导冲压设计、减少试制次数、缩短生产周期,从而降低制造成本,提高生产效率。要提高模拟精度,使仿真模拟更加接近实际成形过程,必须选择合理的本构模型[1],如屈服准则、硬化模型、损伤断裂模型等。轧制板料带有各向异性行为,Hill48屈服准则可以准确预测钢材的屈服轨迹,胡成武[2]利用Hill48平面应力方程和Hill塑性应变比建立了预测任意方向屈服方程,预测DC04和DC05板料在0°、45°、90°的Hill48屈服值,并将结果与试验数据对比,对比结果十分吻合。牛超[3]利用Hill48屈服函数和Swift等向强化本构数值模拟了0°、45°、90°真应力-应变曲线。赵坤民[4]利用ABAQUS/STANDARD进行拉伸仿真分析,得到模拟颈缩后各向异性塑性变形的合适单元。ManSoo Joun等[5]使用刚体-塑性有限元方法分析了拉伸试验结果,迭代后的应力-应变曲线精确地预测了颈缩点,减小了拉伸试验和分析结果的之间的载荷差异。王友德[6]将单轴拉伸试验的载荷-位移曲线作为目标,通过试验-数值耦合方法(NE法),不断迭代修正输入的应力-应变曲线,直至载荷-位移曲线达到要求,即得到真实应力-应变曲线,并比较了NE法较传统理论方法的优点。王玉凯[7]利用ABAQUS/EXPLICIT对Q235冷轧钢进行拉伸断裂数值模拟,验证了Johnson-Cook本构模型对钢材拉伸性能的合理性。陈辉[8]应用TF方法对单轴本构模型进行有限元迭代计算使得模拟计算结果与圆环试样压缩试验结果满足一致性,从而得到304材料的本构关系参数。姚迪[9]基于TF方法模拟的载荷-位移曲线、漏斗根部直径-位移曲线和漏斗变形轮廓线等均与试验结果吻合良好,试样表面模拟应变也与DIC测试结果吻合。蔡力勋[10]基于单轴拉伸真应力-真应变曲线,采用二分法并结合有限元模拟迭代载荷-位移曲线,得到真实反映材料拉伸全程变形特征的等效真应力-真应变曲线。祁爽[11]基于有限元辅助方法得到了四种工程材料的等效全程单轴本构关系,同时分析了应力三轴度。彭云强[12]基于ANSYS APDL语言和有限元辅助方法获得了某型钢的本构关系,并借助ABAQUS中GTN损伤模型预测了裂纹扩展。以上仿真采用的是各向同性屈服准则,未分析各向异性屈服准则的影响。
本文对DC04进行了单向拉伸试验,得到载荷位移曲线和真应力-塑性应变曲线。基于有限元辅助方法,在ABAQUS/EXPLICIT中合理简化拉伸模型,耦合边界条件,引入Hill48各向异性屈服准则,采用动力显示算法和适当质量缩放进行准静态单向拉伸仿真,迭代后的载荷-位移曲线与试验结果吻合,此时得到DC04板材的合理塑性本构,可作为成形仿真的本构输入。最后对比分析了Hill48屈服准则和Mises屈服准则下的仿真结果,结果显示Hill48屈服准则状态下的载荷位移曲线与试验结果符合更好。
1 试验材料及结果
拉伸试验材料为1 mm的DC04冷轧钢板,按照GB/T 228.1-2010[13]切取与轧制方向成0°、45°、90°的标准试样,试样尺寸见图1。拉伸试验在150 kN的电子力学拉伸机上进行,根据GB/T 5027-2007[14],夹头移动速度定为2 mm/min。拉伸断裂试件见图2,由试验所得到的载荷位移曲线见图3,各个方向屈服应力σα和塑性应变比rα见表1。

图1 单向拉伸试样形状及尺寸 (单位:mm)Fig.1 Shape and geometric dimension of uniaxial tensile specimen(unit: mm)

图2 拉伸后的DC04试件(从上到下依次为0°、45°、90°)Fig.2 The specimens of DC04 after stretching(From top to bottom, 0°, 45°, 90°)

图3 单向拉伸试验载荷位移曲线Fig.3 Load-displacement curve of unidirectional tensile test
基于体积不可压缩理论,将工程应力-工程应变按式(1)换算为真应力-应变曲线,去除弹性应变后得到真应力-塑性应变曲线,见图4,将其作为单向拉伸仿真初始本构输入。

图4 真应力-塑性应变曲线 Fig.4 True stress and plastic strain
(1)
式中,σT为真应力,εT为真应变,σE为工程应力,εE为工程应变。
2 有限元数值模拟
2.1 有限元辅助方法
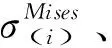

图5 迭代修正方法Fig.5 Iterative correction method
2.2 几何及边界条件
由于考察的是拉伸件的中部区域,由圣维南原理,去除了夹持段和圆角过渡段,留下标距段,尺寸为1 mm×20 mm×80 mm,见图6。

图6 单向拉伸几何模型及边界条件Fig.6 Unidirectional stretching geometric model and boundary conditions
为了模拟边界条件,将模型两边分别设置两个参考点RP1(右端),RP2(左端),位置为过渡圆角与直段的相交中心,按图中坐标为(-60,0),(60,0),将RP1与右端面耦合,耦合位移转角,同理应用于RP2。
2.3 材料模型
采用动力显示算法,需要输入DC04的密度7.85×10-9t/mm3,弹性模量210 000 MPa,泊松比0.3。
塑性本构首次输入试验真应力-塑性应变曲线,这里以真应力和塑性应变表格形式,将拟合曲线输入到ABAQUS塑性属性设置中,需要注意的是真应力为递增形式,在循环迭代本构后,重新输入塑性表格数据时需去除递减真应力段。
由ABAQUS手册,对于板料(平面应力状态),Hill48各向异性屈服准则中的应变比R11,R22,R33,R12,R13,R23用各向异性系数r值表示为
R11=R13=R23=1
(2)
(3)
(4)
(5)
按公式2~5,DC04的R11,R22,R33,R12,R13,R23值见表2。由于引入各向异性,需要定义材料主方向,这里定义几何模型纵向为材料主方向。

表2 Hill48屈服准则的应变比参数
2.4 分析步及网格设置
由于采用准静态单向拉伸仿真,所以分析步采用动力显示分析,时间间隔为0.1 s,对几何模型进行适当的质量缩放,后续分析表明质量缩放因子取1000,满足准静态仿真要求。
由于要循环修正真应力和塑性应变,所以在ABAQUS场输出中需勾选MISES,PEEQ作为修正结果,考虑计算效率,时间均匀间隔200。
为了分析计算结果,得到载荷位移曲线,需要在历史输出中勾选参考点RP1的支反力RF1及纵向位移U1,同理,时间均匀间隔200。
整体网格尺寸为1,厚度方向布置了4个种子,将厚度方向分割了3段,中间部分对纵向边线增加种子个数,实现网格细化,见图7。在仿真中总结经验,调节单元类型,其中各向异性采用非协调模式。

图7 网格模型Fig.7 Grid model
3 仿真结果
3.1 准静态分析
在ABAQUS/EXPLICIT中,能量平衡方程可以表示为
constant=ETOT=EI+EV+EFD+EKE-EW
(6)
其中,EI为内能(包括弹性应变能、塑性应变能和与沙漏控制相关的伪能),EV为粘性机制耗散的能量,EFD为摩擦耗散的能量,EKE为动能,EW为外力功,ETOT为系统的总能量。
由于不存在粘弹性材料、离散的减震器及材料阻尼,所以粘性机制耗散的能量EV很小。单向拉伸仿真没有摩擦,故EFD为零。只剩下EI+EKE-EW,因此对于单轴拉伸仿真,若变形材料的动能EKE占内能EI的比例很小(一般为1%~5%),那么拉伸试件的外力功EW约等于试件的内能EI,那么仿真就是准静态的。
从图8中可以看出,整个模型的动能ALLKE(红色曲线)对时间的积分只占整个模型内能ALLIE(蓝色曲线,基本与X轴重合)对时间积分的很小部分,所以是准静态的。

图8 准静态拉伸能量历程 Fig.8 Quasi-static tensile energy history
3.2 Hill48屈服准则下的载荷位移曲线分析
单向拉伸仿真得到等效Mises应力、等效塑性应变PEEQ云图见图9、10,局部出现颈缩,颈缩区域中间单元的等效Mises应力与等效塑性应变PEEQ即为新的塑性本构。按照图5的修正方法,对材料本构进行了两次迭代,每次迭代仿真后的载荷位移曲线及与试验数据的标准差见图11。

图9 等效应力云图(单位:Mpa) Fig.9 Equivalent stress cloud(unit: MPa)
从图11中可以看出,将单向拉伸试验数据以真应力-塑性应变的形式输入,经过单向拉伸仿真后的载荷位移曲线与试验数据的标准差为959.01,差异主要在损伤断裂阶段,说明单向拉伸试验中颈缩部分的本构数据无法准确描述损伤断裂段,因此需要对本构进行修正。采用迭代修正方法对塑性本构进行第一次修正后的仿真载荷位移曲线与试验数据标准差为215.82,误差下降约3.4倍,经过仿真后的载荷位移曲线在弹性和塑性强化阶段与试验数据吻合,损伤断裂段开始接近试验曲线,损伤断裂的本构得到有效修正。经过第二次迭代修正后的仿真载荷位移曲线与试验数据的标准差为208.89,与试验数据的差距进一步变小,标准差相对于第一次修正下降明显变缓,此时的真应力-塑性应变曲线(见表3)即为目标本构,可应用于汽车零部件的冲压成形仿真。

图10 等效塑性应变云图 Fig.10 Equivalent plastic strain cloud

图11 迭代仿真后的载荷位移曲线 Fig.11 Load-displacement curve after iterative simulation based

表3 迭代后的真应力-塑性应变本构
3.3 两种屈服准则下的载荷位移曲线对比
从图12中可以看出,Hill48屈服准则状态下的载荷位移曲线和Mises屈服准则状态下的结果在弹性阶段和塑性强化阶段一致,在损伤断裂段出现差异,且与试验数据的标准差分别为959.01和527.87,说明屈服准则对仿真损伤断裂段影响较大。
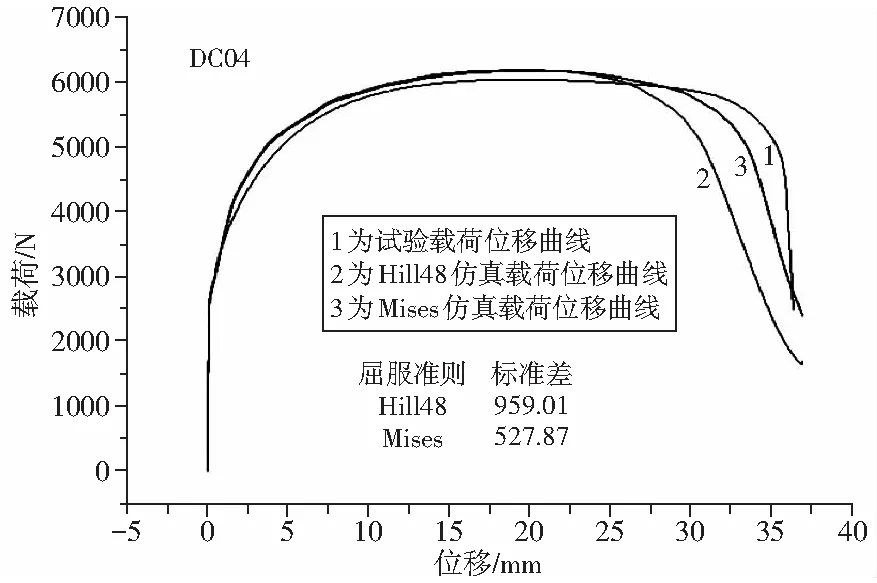
图12 不同屈服准则下的仿真结果Fig.12 Simulation results under different yield criteria
从图13中可以看出,塑性本构经过第一次迭代后,Hill48屈服准则状态下的载荷位移曲线和Mises屈服准则状态下的仿真结果与试验数据的标准差分别为215.82和330.00,Hill48屈服准则下的仿真结果标准差更小。

图13 第一次迭代仿真后的结果Fig.13 Results after the first iteration of the simulation


图14 第二次迭代仿真后的结果Fig.14 Results after the second iteration of the simulation
4 结论
1)按照单向拉伸试验标准,得到DC04(厚度1 mm)薄板的0°、45°、90°载荷位移曲线,真应力-塑性应变曲线,各向屈服应力和塑性应变比。
2)合理简化了单向拉伸仿真模型及显示动力计算,仿真结果表明模型有效,且经分析达到了准静态要求。

4)通过对比Hill48屈服准则和Mises屈服准状态下的仿真结果,发现不同的屈服准则对损伤断裂阶段影响不同,Hill48各向异性屈服下的载荷位移曲线与试验结果的一致性较各向同性Mises屈服准则更好。
