基于Petri网的即时情报服务系统工作流建模和分析

2021-07-19刘晓晖冯菲第五念东

电脑知识与技术 2021年13期

刘晓晖冯菲第五念东

摘要：基于Petri网络建立工作流，既可以将Petri网络作为图形化的建模工具，同时又可以利用它坚实的数学定义，对模型做出精确的分析，可以降低建模难度、简化过程，同时又能保证所建模型的正确性。本文通过对即时情报服务系统的业务流程分析，提出了一个基于Petri网络的即时情报服务系统工作流模型，并对该工作流模型进行正确性分析。该模型成功应用于即时情报服务系统建设中。

关键词：Petri;工作流

中图分类号：TP393 文献标识码：A

文章编号：1009-3044（2021）13-0235-02

Abstract： Real-time intelligence service system is a typical workflow system， this paper applies Petri for modeling real-time intelligence service， and analyses the workflow modeling.

Key words： Petri; Workflow

1 前言

按照国际工作流管理联盟（WfMC）对工作流的定义：工作流是能够完全或者部分自动执行的过程。工作流建模是完成对目标系统业务过程的抽象表示，主要解决工作流流程的描述，在工作流合理性验证上缺乏相应的数学模型。应用Petri网络建立工作流，既可以将Petri网络作为图形化的建模工具，同时又可以利用它坚实的数学定义，对模型做出精确的分析。本文基于Petri网络对即时情报服务系统工作流进行建模，同时给出即时情报服务系统工作流合理性分析。

2 基本概念介绍

2.1 Petri网

德国科学家Carl Adam Petri提出的Petri網，是以双边有向图来描述业务过程，该方法利于分析和正确性验证，并具有精确的数学定义和数学基础，是工作流建模和分析的有力工具。

Petri网是一个三元组（P，T，F）， P：库所的有限集，T：变迁的有限集;F ：一个P元素和一个T元素组成的有序偶的集合，其充分必要条件是：

⑴ P ∩ T=? ;

⑵ P ∪ T≠? ;

⑶ F[?]（P×T）∪（T×P）（ ×为笛卡尔积）;

⑷ dom （F） ∪ cod（F ） = P ∪ T ;

其中

dom（F） = { x∣[?]y ：（x，y） ∈ F }

cod（F） = { y∣[?]x ：（y，x） ∈ F }

分别为F 的定义域和值域。

2.2 工作流网络

工作流网是在Petri 网的基础上用来对工作流的合法性、有效性进行验证，包括顺序、并行、选择和循环四种路由结构，工作流所有执行结构都可由这四种路由结构组合而成。

2.3 工作流网络合理性验证

工作流模型的合理性、有效性是模型分析的主要部分，需要从工作流模型出发，保证模型不存在结构上和行为上的死锁状态[5]。国内外很多学者采用文献[6]中对工作流合理性的定义，即工作流网是合理的，只有它的每一个变迁都属于一条从开始状态M0到终止状态M的执行序列上;当终止库所拥有，其他库所没有令牌时;模型中不存在执行不到的节点，即没有死锁。

3 即时情报服务系统模型

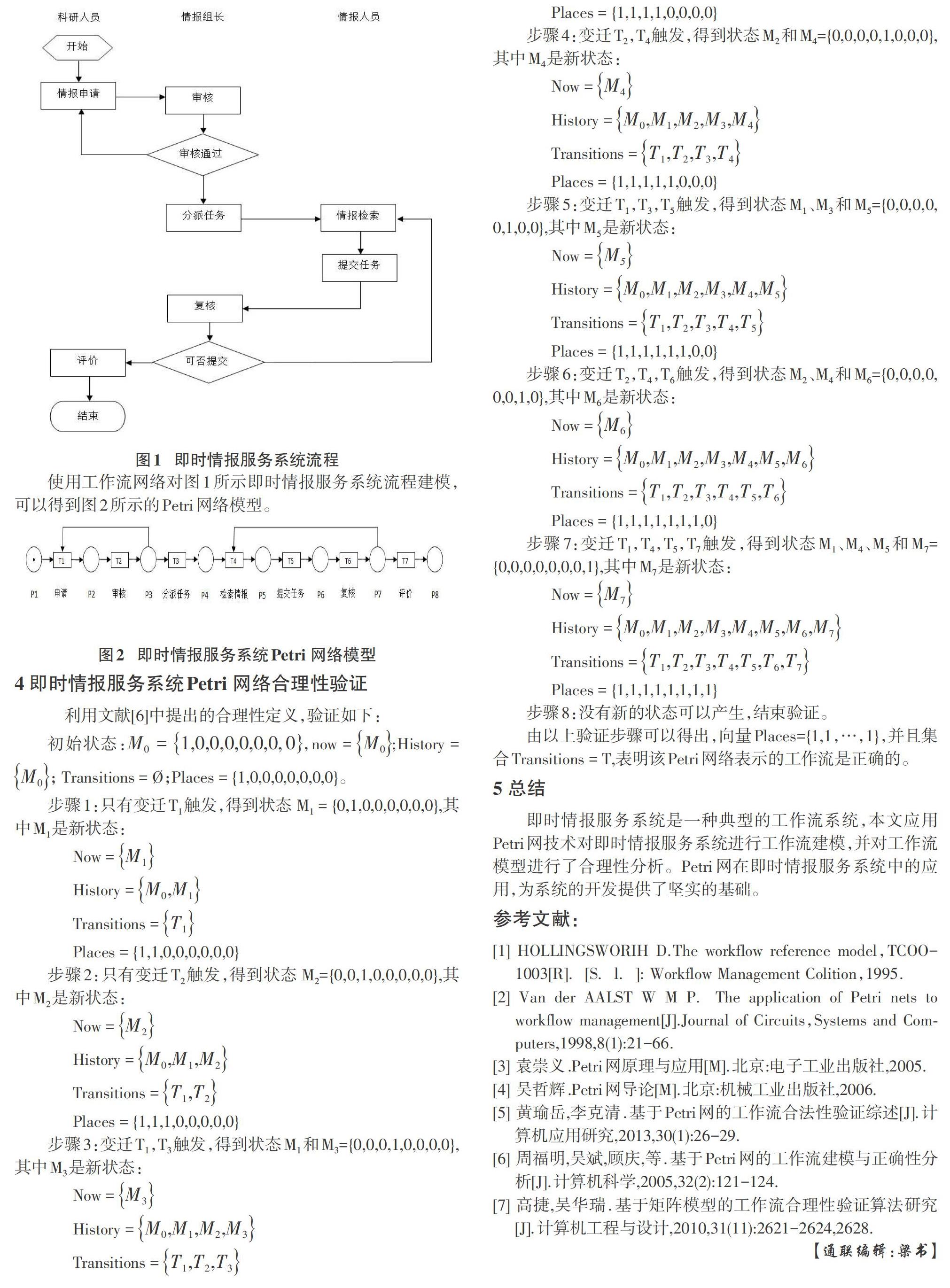
即时情报服务系统是利用单位网络平台，通过网上流转，提高情报服务的快捷和方便性，对科研生产提供支持和保障作用。如图1所示，即时情报服务系统流程图如下：

使用工作流网络对图1所示即时情报服务系统流程建模，可以得到图2所示的Petri网络模型。

4 即时情报服务系统Petri 网络合理性验证

利用文献[6]中提出的合理性定义，验证如下：

初始状态：[M0=1，0，0，0，0，0，0，0]，now = [M0];History = [M0]; Transitions = ?;Places = {1，0，0，0，0，0，0，0}。

步骤1：只有变迁T1触发，得到状态 M1 = {0，1，0，0，0，0，0，0}，其中M1是新状态：

Now = [M1]

History = [M0，M1]

Transitions = [T1]

Places = {1，1，0，0，0，0，0，0}

步骤2：只有变迁T2触发，得到状态 M2={0，0，1，0，0，0，0，0}，其中M2是新状态：