用聚类分析和时间序列模型对音乐因素进行定量分析

李春雨 石虔韩 伍尚乐

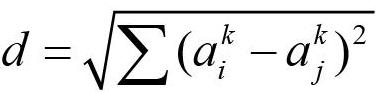
【摘  要】本文基于2021年美赛建模D题。为了量化音乐的影响，首先，我们创建一个表示音乐影响的加权邻接矩阵，在这个矩阵网络中，我们关注最后两个指标：总和和出圈率。然后，我们创建一个子网络来显示我们的“音乐影响力”指标揭示了什么。下一步为了找出音乐的相似度，我们采用了聚类分析的方法。该方法首先对给定的数据进行预处理和距离归一化。然后，利用欧几里德距离对相似度进行量化，距离越短，音乐家（或流派）之间就越相似。最后运用时间序列模型分析音乐是如何随着时间的推移而变化的。

【关键词】邻接矩阵;聚类分析;时间序列模型

1.概述

音乐自古以来就是人类文化的一部分。有时，音乐会发生进化和革命性的變化，这在音乐的发展过程中具有重要意义。因此，我们有必要建立一个衡量音乐影响的模型，并应用它来研究音乐是如何随着时间而变化的。首先，我们需要构建加权邻接矩阵来连接影响者和被影响者，并创建一个子网络来显示我们的“音乐影响”度量所揭示的内容。然后，我们需要探讨同一流派和不同流派音乐家的相似度，不同流派的相似度以及影响者和追随者的相似度。最后我们需要分析音乐是如何随着时间而发展的。

2.加权邻接矩阵

2.1加权邻接矩阵说明

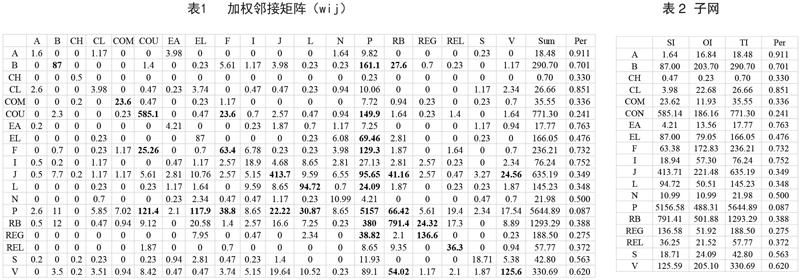
邻接矩阵是表示不同流派之间关系的方阵，其维度数是流派的个数，而加权邻接矩阵是赋予数值不同权重的邻接矩阵。我们用Wij表示i行类型影响j列类型的次数，用wij表示加权邻接矩阵的条目，它对应于i行类型对j列类型的影响程度。

说明：（1）取流派名称的前几位字母表示（2）wij由Wij加权后乘以10000获得;（3） Sum是一行wij的和，Per是对其他流派的影响程度占总影响程度的百分比，即出圈率;（4） 大于20的数值标为粗体。

2.2子网

使用上面的加权邻接矩阵，我们现在创建它的子网络。如表2所示：

说明：（1）SI是指对流派内的影响程度;（2） OI是指对其他流派的影响程度;（3）TI表示影响的总程度。

通过对加权邻接矩阵和子网络的分析，得出结论：TI（Sum）越大，总影响程度越大;Per值越大，对其他流派的影响程度的占比越大，即越出圈。比如前卫派（A），它的TI值很小，Per值最大，也就是说，这个流派虽然影响很小，但是主要是对其他大多数流派的影响。

3. 欧几里德距离矩阵

聚类分析是多元统计分类学的一种形式，其基本思想是根据表征样本的特征变量的相似度，将具有相似性质的变量归为一类，将具有不同性质的变量归为另一类。在对变量进行排序之后，我们可以直接分析类别。该方法首先对给定的数据进行预处理和距离归一化。然后，利用欧几里德距离对相似度进行量化。距离越短，音乐家（或流派）就越相似。

3.1预处理

在预处理过程中，我们首先排除了一些不太相关的变量，如艺人姓名、艺人编号、人气、发行日期和歌曲标题。因此，我们得到了我们需要的12个样本指标，它们是可舞性、能量、配价、节奏、响度、模式、音调、声学、乐器性、活性、言语性。注意，因为音调中没有-1，即不存在缺失数据的情况，我们可以直接统一进行下一步。

3.2 距离归一化

我们注意到不同值之间的数量级不同，因此，我们对上述12个样本指标数据组执行范围归一化。范围归一化是对一系列值（x1，x2，…，xk，…，xn）进行归一化的过程，其中max{x}，min{x}分别表示最大项和最小项，我们使用以下公式将xk转换为xk?：

其中xk 属于 [0，1].

3.3音乐相似性度量

在这一部分中，我们使用欧几里德距离来量化相似度，相似度的计算公式如下：

3.4音乐家欧几里德距离矩阵

为了探讨音家之间的相似程度，我们随机选取10位音乐家来计算他们的欧几里德距离。它们是blink-182 （a1）， Misfits （a2）， Coldplay （a3）， The Replacements （a4）， Sarah Vaughan （a5）， Julie London （a6）， Michael Jackson （a7）， The Isley Brothers （a8）， John Lee Hooker （a9）， and Johnny Cash （a10）。然后得到欧几里德距离矩阵，如表3所示：

欧几里德距离越小，音乐家就越相似。根据我们的计算，同一流派的平均欧氏距离为0.663，而不同流派的平均欧氏距离为1.178，这意味着同一流派的音乐家比不同流派的音乐家更相似。

3.5流派欧几里德距离矩阵

为了进一步探讨不同流派之间的相似度，我们利用欧几里德距离公式来计算不同流派之间的欧几里德距离。然后得到流派之间的欧几里德距离矩阵，如表4所示。同样地，欧几里德距离越小，流派间就越相似。因此，我们认为欧几里德距离的数值是区分流派的指标。例如，蓝调（B）和儿童音乐（CH），蓝调（B）和乡村音乐（COU），它们的欧几里德距离很小，因此它们相对更相似。另一方面，宗教音乐（REG）和古典音乐（CL）、流行摇滚（P）和新生代音乐（N），它们的欧几里德距离很大，因此它们的相似性相对较小。以图1用树状图进行详细展示：

3.6影响者和追随者的欧几里德距离

下面为了探讨影响者与追随者的相似度，我们使用欧几里德距离公式来计算他们的欧几里德距离。对于同一流派的影响者和追随者，我们只是随机选择一对，而对于不同流派的影响者和追随者，我们随机选择一对来自不同流派的影响者和追随者。然后，我们得到了影响者和追随者的欧几里德距离，如表5所示：

从表5可以看出，同一流派和不同流派的影响者和追随者的欧几里德距离平均值分别为0.656和0.831，表明影响者确实影响追随者，但影响程度不同。同一流派内的距离较小，表明影响程度较高，而不同流派的距离较大，影响程度较低。

4.时间序列模型

为了分析流派如何随着时间的推移而变化，我们采用了时间序列模型。通过该模型，我们可以很容易地了解流派的变化趋势。为了消除偶然因素影响下随机波动的影响，我们采用历史数据进行统计分析，并对数据进行适当处理，预测趋势。对于序列{t1，t2，…，tn}和α属于（0，1），令t1?=t1，我们应用以下公式，其中α=0.45：

因为音调的变化杂乱且与时间无关，可舞性和节奏等6种指标相对稳定，因此我们主要关注四个指标：能量、响度、人气和声学。可以看到能量、响度和人气呈上升趋势，而声学指标呈下降趋势，表明音乐的确随时间变化。如图2所示：

5 .模型评价

（1）通过归一化，成功地将因子转换为同一维度[0，1]。因此，可以通过欧几里德距离来衡量音乐家和流派之间的相似性。

（2）利用时间序列模型得到了一些因素的变化趋势，消除不规则波动。

参考文献

[1]黄家庆。论音乐在社会文明发展中的作用[J]。新疆师范大学学报（哲学社会科学版），1990（02）：92-95+105.

[2]邹璐。音乐教育在社会发展中的作用[J]。现代传播，2012（01）：255.

[3]钱小刚、朱志强。聚类分析[J]。栽培与栽培，1987（06）：44-48.

[4]司守奎、孙兆良。数学建模算法及应用[M]。Beijing：National Defense 工业出版社，2020：167-171.