自转离心力对月幔温度演化影响的二维有限元模拟
2021-07-19张腾,钟振
张 腾,钟 振
贵州师范大学 物理与电子科学学院,贵阳 550025
通过月球影像研究,人们发现其正面分布着大量暗黑色的玄武岩沉积物. 相关研究表明,这些玄武岩主要由月球形成初期的古火山活动产生. 到前苏联月球3号首次拍摄月球背面时,发现月球背面并不像正面那样,除莫斯科海、南极艾得肯盆地及Apollo撞击坑外,其他区域没有任何玄武岩[1]. 进一步的研究表明,月球背面玄武岩含量约占整个背面的1%,而正面玄武岩含量占正面区域的1/3. 月球正面和背面玄武岩含量的不对称性,间接地反映了早期热演化的不对称性. 关于月球形成初期的状况,目前学界已确认了岩浆洋模型(lunar magma ocean,LMO)的合理性[2]. 该模型认为,月球自吸积后,发生了全球性的熔融事件,较轻的钙长石由于结晶,浮于岩浆洋的顶层,形成原始的斜长岩月壳,而较重的镁铁质物质下沉,结晶形成月幔. 在结晶过程中,全球性对流模式可能导致背面月壳增厚,而正面月壳变薄,易产生古火山活动[3]. Zhong等人[4]研究表明,1阶对流项会导致热演化的不对称性. Laneuville等人[5]研究表明,由于正面风暴洋一带富集KREEP产热元素,局部区域的高温,会引起月幔热对流趋向于正面产生,导致热演化的不对称性. Padovan等人[6]的研究也表明,发生在月球背面的一次大碰撞使月幔熔融逆向,导致热演化的不对称性. 月球激光测距(lunar laser ranging,LLR)数据表明地-月间距以每年3.8 cm的速度增加[7],由地-月系角动量近似守恒,可知月球自转速度在不断地变慢,早期古月球自转速度比现在大得多,自转离心效应对热演化的影响不能被忽略. 有关自转离心效应对月球热演化的影响,目前还没有类似的研究与分析. 为此,本研究考虑热对流效应,顾及自转离心力的影响,利用有限元方法,对月幔温度演化进行模拟,以探究自转离心效应与月球热演化的关系,以期为这方面的研究提供一定的参考.
1 无量纲化的控制方程和粘滞系数
考虑对流效应的月球热演化,控制方程较为复杂,为了便于边界条件的处理,通常采用有限元方法来进行仿真分析[8]. 在对流模型中,月幔通常被认为是一种不可压缩的高粘滞性流体,即不考虑惯性力的影响,与此相关的湍流效应忽略不计,学界将此模型称为Boussinesq近似. 在该近似条件下,仅在动量方程的浮力项中考虑密度的变化,其他控制方程的密度假定为常数[9-10]. 为了检验自转离心效应,控制方程仅考虑热对流效应,与此有关的化学物质分层效应忽略不计[11]. 控制方程主要由质量方程、动量方程和能量方程构成[9-12]. 这3个方程中相关物理量直接参与运算,不便于有限元网格的构建,为此,通常将控制方程进行无量纲化处理. 假定无量纲化的速度矢量为u′,二阶应力张量为σ′,压强为P′,温度和热产能率分别为T′和H′. 有量纲参考值及对应无量纲值,以及相关计算参数见表1. 此时,质量方程、动量方程和能量方程的无量纲形式为
其中Ra表示瑞利数,其大小为
(4)
其中:ρ0和g分别表示月幔参考密度和参考重力加速度,μ0和k0分别表示参考黏度和热扩散系数,β和ΔT0分别表示热膨胀系数和核幔界面温度,R0表示月球平均半径R与内核半径Rcore之差. 相关参数取值[8,11]见表1.

表1 相关参数的有量纲参考值及无量纲值
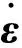
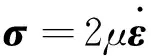
(5)
月幔粘滞特征是影响热演化的重要因素,它使得月幔在长周期时标内表现出流体特征,而在短周期时标内表现出弹性特征. 月幔粘滞特征通常用粘滞系数μ来量化,其大小通常与温度、压强和研究区域的大小有关[13]. 为了简化运算,将月幔物质的流体特征假定为牛顿流体[3-5],此时,剪应力与应变速度成正比. 假设参考黏度为μ0,核幔边界温度与壳幔边界温度之差为ΔT,对于月幔中参考半径d处的某点,假定该点的温度为T,可得月幔物质的黏度[14]为
(6)
其中,R表示月球平均参考半径,b和c为给定常数,取b=ln2.5,c=ln2.0[14].
2 控制方程的弱解形式
进行有限元程序设计前,首先需要推导微分方程的弱解形式. 为了便于公式推导,将(1)-(4)式中的撇号去掉,因此,后文的所有参量均表示无量纲化. 数值模拟在直角坐标系中进行,研究区域为月幔某一经线的剖面. 根据变分基本引理,结合(4)式得到(2)式的弱解形式为
(7)
其中:vx和vy分别表示试探函数v在x轴和y轴方向的分量,gx和gy分别表示x轴和y轴方向的无量纲化有效加速度,wij为试探函数v对应的二阶应变率张量. 若不考虑边界作用时[11],(7)式可以简化为
(8)
其中二阶应力张量σij与试探函数v的应变率张量wij分别为
类似地,(3)式的弱解形式为
(11)
其中:Tk+1表示当前时刻的待求温度,Tk表示上一时刻的温度,τ表示温度对应的试探函数,δt表示相邻两时刻之间的步长.
3 月球的自转离心力
3.1 自转角速度
月球的潮汐效应能使地球自转速度不断的变慢,该效应由LLR数据得到验证[7]. 由于地球自转速度受自身惯量矩变化和太阳潮汐的作用,两者的影响在量级上相同而方向相反,并且其他行星的潮汐因距离很远导致影响很小,比如木星的潮汐影响在量级上只有太阳的万分之一,因此,地球和月球可以看作是一个孤立系统且总角动量近似守恒. 总的角动量包括:地球自转角动量、月球自转角动量、月球绕地球的公转角动量. 根据月球形成的巨型撞击理论,文献[15]的研究表明,月球形成时与地球的距离为3.77R⊕(R⊕表示地球半径),得到早期地-月系间距约为2.4×107m. 文献[16]的研究表明,月球形成初期的地-月系总角动量,比当前系统角动量多出10%到20%. 本研究取多出的系统角动量为14%,结合表2数据估算出早期的地球自转周期为5.05 h,相应的月球自转角速度为4.4×10-3rad/s. 文献[17]的数值结果发现,地-月系形成初期地球自转周期约为5 h,本研究的计算结果与其接近,表明本研究求解的早期月球自转角速度具有一定的合理性.
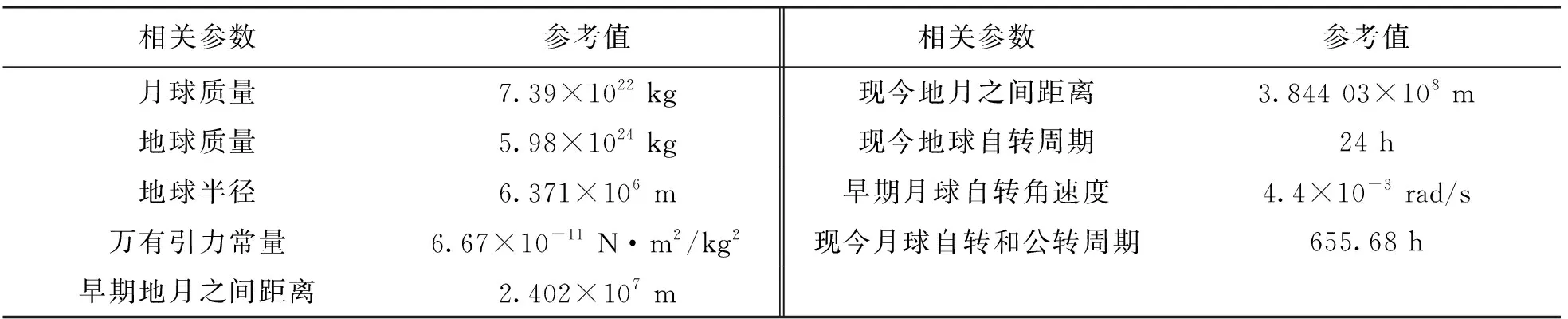
表2 计算离心力用到的相关参数
3.2 自转离心力的计算
如图1所示,以与黄道面平行的方向为x轴,其法线方向为y轴,月球中心为坐标原点,建立二维直角坐标系,z轴为自转轴. 由文献[18]可知,月球自转轴与黄道面法线的夹角约为1.6°(即为角θ). 所以得到实际月球截面上某一点的转动半径为
R1=R·rcos(θ+φ)
(12)
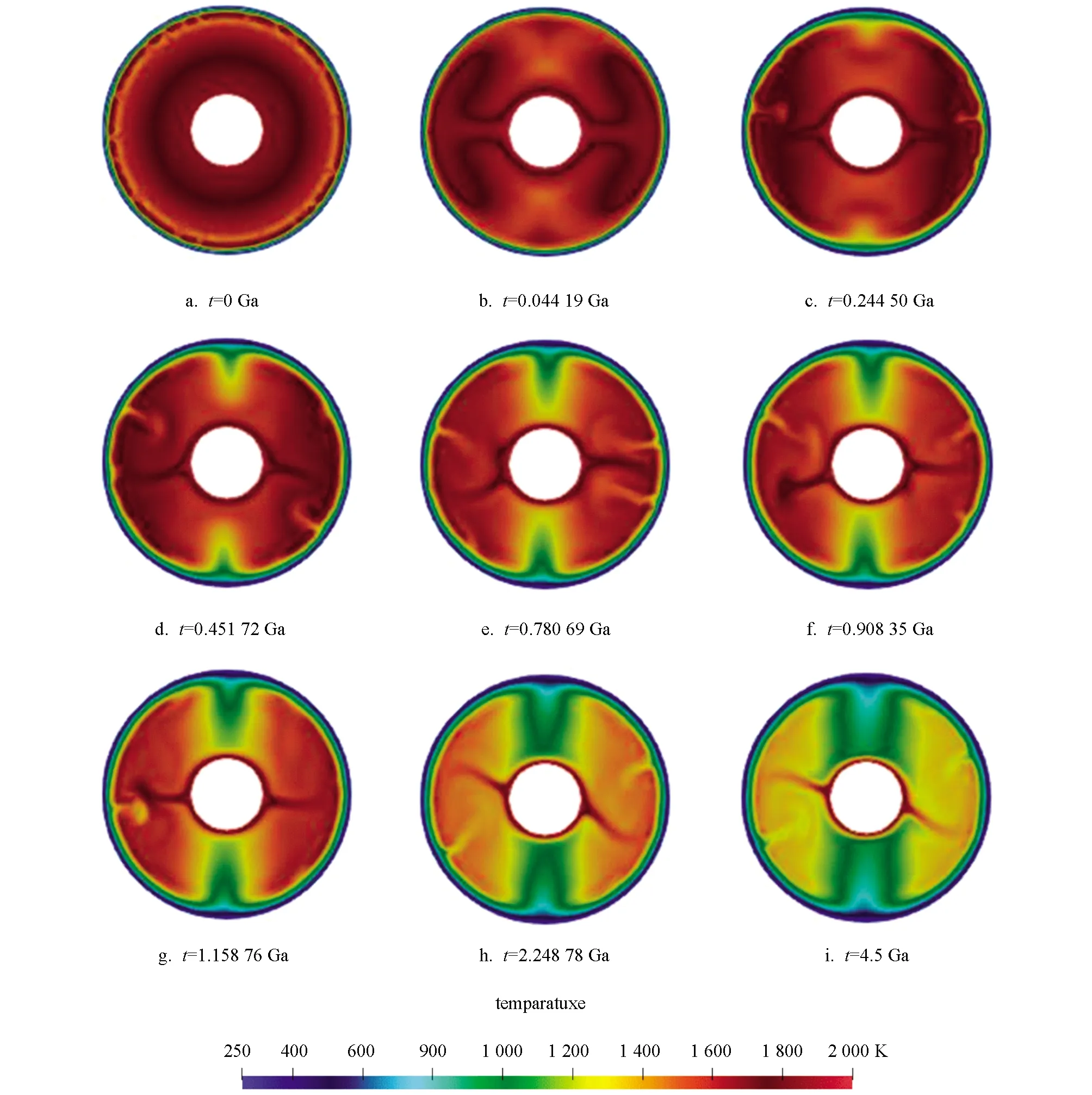
其中:r表示图1圆形区域上某一点的半径,且满足0 图1 自转离心力示意图 其中:ω表示月球的自转角速度,根据(13)和(14)式,得到(7)式中无量纲化的有效加速度为 目前,月球被公认起源于一次火星大小的天体与地球的碰撞,自吸积结束后,较重的金属元素下沉引起重力势力的释放,以及短周期放射性元素26Al的作用,致使月球内部温度快速上升. 另外,根据阿波罗任务采样的岩石样品研究结果,发现月球早期拥有较高的温度,在月球形成的初期,月幔处于高温和完全熔融的状态[2,8]. 基于此考虑,本研究假定月球形成初期具有高温月幔,同时假定月幔处于完全熔融状态[8]. 参考文献[8],取核幔边界温度为2 000 K,演化时间为4.5 Ga(1 Ga=10亿年). 月幔初始温度见图2a,从核-幔边界向外,温度逐渐降低,此时,整个月幔的平均温度约为1 667.76 K. 由于自转离心效应,至图2b时(演化时间约为4 419万年),在垂直自转轴的方向形成对流柱,将核-幔边界的热量输运至外表面,同时,在两极区域,即将形成低温下沉的对流柱,此时,整个月幔的平均温度约为1 608.93 K. 文献[11]的研究表明,当不考虑自转离心效应时,产生均匀的4个对流柱,这说明自转离心效应有必要在月球热演化中加以考虑. 如图2c所示,至0.245 50 Ga时,月幔温度不断地下降,由于内部热量的减小,无法提供充足的能量,致使对流柱变得不稳定,而两极的低温对流柱已形成,此时,整个月幔的平均温度约为1 559.67 K. 至0.451 72 Ga时(图2d),由于内部能量的降低,同时,两极大幅度的低温对流柱带来的低温,致使核-幔边界的热对流柱发生切向移动,外表面原高温区产生小幅度的低温对流柱,此时,整个月幔的平均温度约为1 520.38 K. 如图2e和图2f所示,从0.780 69 Ga至0.908 35 Ga,由于月幔温度的进一步降低,两极大幅度低温对流柱,以及外表面原高温区小幅度低温对流柱的共同作用,使得核-幔边界有产生小幅度的热对流柱. 如图2g-图2i所示,从1.158 76 Ga至4.5 Ga,两极大幅度低温对流柱相对稳定,其他小幅度低温对流柱,以及核-幔边界的高温对流柱不稳定,特别是核-幔边界的对流柱会产生明显的切向移动. 由图2a-图2i可知,自转离心效应有助于在垂直于自转轴的方向,于核-幔边界产生热对流柱,在两极区域产生明显的低温对流柱,进而快速地输运月球内部的热量. 不同温度对应的颜色图2 月幔温度随时间的变化 另外,文献[11]在不考虑自转离心效应时,月幔初始(0 Ga)平均温度约为1 735.10 K,至4.5 Ga时约为1 278.20 K,下降456.90 K. 而本研究考虑自转离心效应后(表3),月幔初始平均温度约为1 667.76 K,至4.5 Ga时约为1 163.28 K,下降504.48 K. 本研究模拟的最终月幔温度低于文献[11],且两者从初始到0.245 50 Ga时,分别下降28.28 K和108.09 K,这说明自转离心效应引发的对流模式,降低了月幔的温度,并且在月球热演化的前0.245 50 Ga更为明显. 由图2可知,在核-幔边界处,垂直于自转轴方向产生两个热对流柱,对流柱产生的方向恰好是月壳厚度二分性的方向,因此,自转离心现象可能与月壳二分性相联系,可为月球不对称热演化研究提供一定的参考. 表3 不同演化时间点的月幔平均温度 基于月球自转速度减慢的事实,以及利用地-月系角动量近似守恒的原理,估算了月球早期较大的自转角速度. 在月球热演化的控制方程中考虑自转离心力后,① 发现自转离心效应有助于在月球形成初期,在垂直于自转轴方向,于核-幔边界处产生热对流柱;② 随着内部热量输运至月表,在两极区域产生大幅度、稳定的低温对流柱;③ 随着月幔温度的进一步降低,外表面原高温区产生小幅度的低温对流柱,核-幔边界的高温对流柱会产生切向移动;④ 由自转效应引起的对流模式,能有效降低月幔的温度,对月幔温度起到一定的调节作用.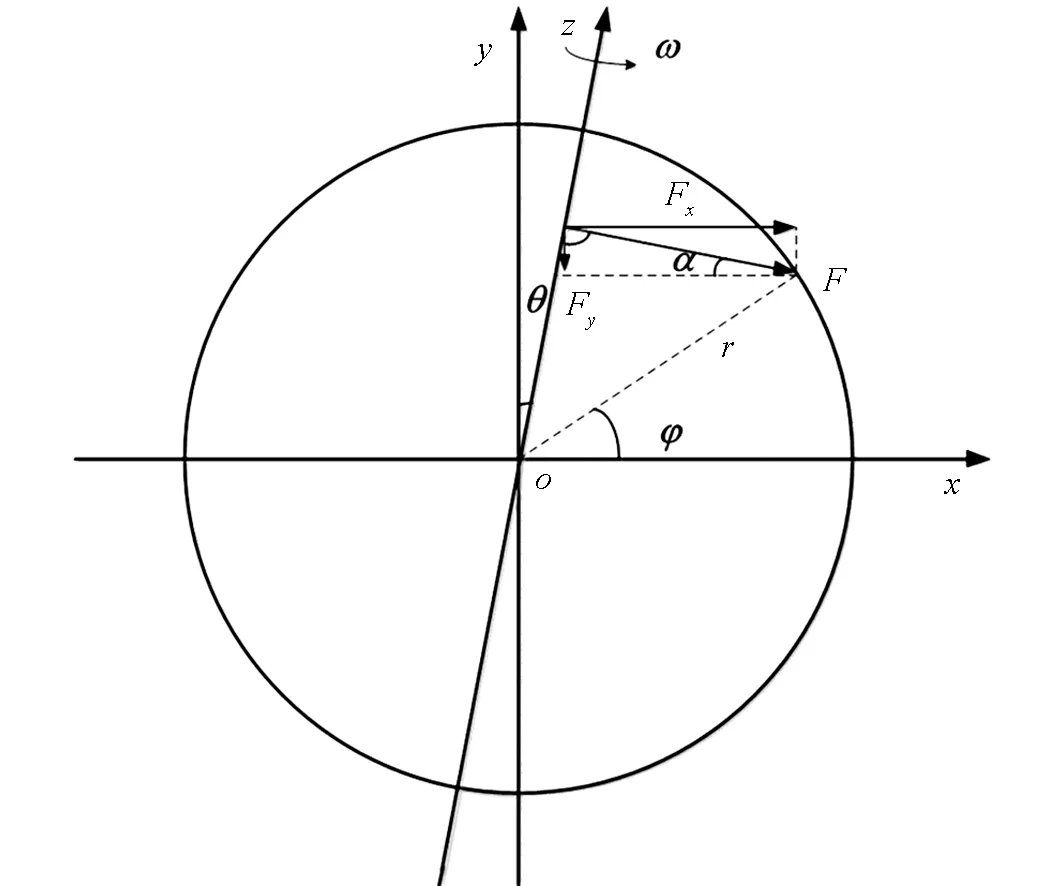
4 数值模拟

5 结 论
