改进共轭梯度法的收敛性
2021-07-19林穗华
林 穗 华
广西民族师范学院 教育科学学院,广西 崇左 532200
解极小化问题min{f(x)|x∈Rn}的迭代法有多种,其中共轭梯度法由于无须用到2f(x)等n阶矩阵数据,存储需求少而特别适合大规模优化问题[1-18]. 传统共轭梯度法的迭代格式为:
xk+1=xk+αkdk
(1)
(2)
其中:dk为搜索方向,αk为步长因子,βk为参数,gk=f(xk),sk=xk+1-xk. 不同的βk参数公式对应不同的共轭梯度法. 著名的PRP,HS,LS,FR,DY,CD方法的参数公式如下:
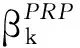
其中
相应的WYL,MHS,MLS方法都具有较好的收敛性.
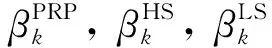
(3)
其中:
这一修改方式能确保βk≥0,但却无法满足充分下降条件:∃c∈(0,1),使
(4)
然而某些类型共轭梯度法的收敛性依赖于充分下降条件,因此文献[11]定理1只得将“满足充分下降条件”作为预设前提. 事实上VPRP,VHS,VLS方法不满足充分下降性,其全局收敛性仍无法保证.
受文献[9-10,16-17]充分下降性策略的启发,我们修改(3)式的分母,得到
(5)
(6)
(7)
其中常数μ>2. 我们将讨论(1),(2)式迭代法的收敛性,其中参数βk取自(5),(6)或(7)式,步长因子αk考虑采用经典的weak Wolfe-Powell(WWP)线搜索[2]及文献[18]针对BFGS和PRP方法设计的modified weak Wolfe-Powell(MWWP)线搜索.
记参数为δ,σ的WWP线搜索条件为WWP(δ,σ)条件:
(8)
(9)
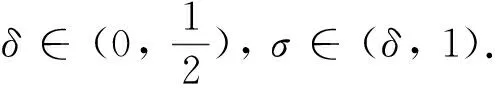
记参数为δ1,δ,σ的MWWP线搜索条件为MWWP(δ1,δ,σ)条件:
(10)
(11)
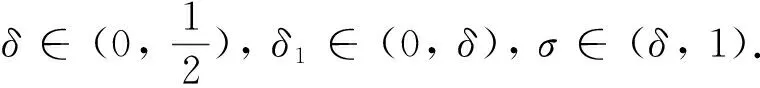
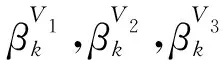
1 算法及性质
算法V-WWP
步骤1设定初值x1∈Rn,μ>2,0<δ1<δ<σ<1,ε>0,d1=-g1,k=1. 若‖gk‖≤ε,则停止.
步骤2计算αk满足WWP(δ,σ)条件(8)和(9)式.
步骤3由(1)式计算xk+1. 若‖gk+1‖≤ε,则停止.
步骤4由(5),(6)或(7)式计算βk+1,由(2)式计算dk+1.
步骤5置k=k+1,转步骤2.
在算法V-WWP框架中,将步骤2改为计算αk满足MWWP(δ1,δ,σ)条件(10)和(11)式,则得到V-MWWP算法.
定理1算法V-WWP生成的序列βk,gk,dk满足0≤βk和充分下降条件(4).
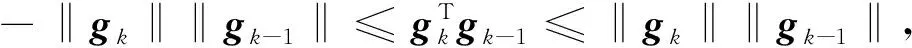
(12)
又有
(13)
(14)
(15)
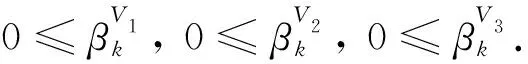
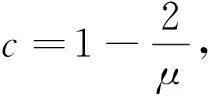
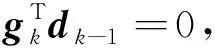
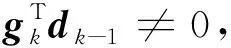
从而可得
进一步可得
定理1得证.
2 原理与假设
证明算法的收敛性需要用到以下假设和引理.
假设:
‖g(x)-g(y)‖≤L‖x-y‖ ∀x,y∈N
(16)
引理1[3,6]考虑满足如下条件的任一共轭梯度法(1)-(2):
(a)βk≥0.
(b) 搜索方向满足充分下降条件(4).
(c) 以下Zoutendijk条件成立:
(17)
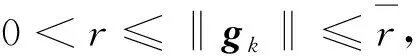

以下算法收敛性分析中均假设‖gk‖≠0,否则算法已得到f(x)的稳定点而终止.
3 全局收敛性
定理2若假设和成立,则算法V-WWP生成的序列gk,dk满足Zoutendijk条件(17).
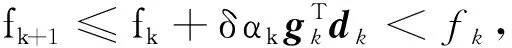
从而可得
(18)
由(8),(18)式可得
(19)
(19)式两端对k=1,2,…求和,可得
从而可知(17)式成立,定理2得证.
定理3若假设和成立,βk,gk,dk为算法V-WWP生成的序列,则βk满足性质(*).
证由(9)式和定理1,可得
‖gk-1‖2≥c(1-σ)‖gk-1‖2
从而可得
根据算法V-WWP步骤(4)βk的取法,可知
(20)
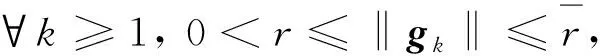
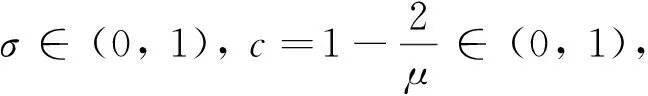
由(12)和(20)式,可得
设‖sk-1‖≤λ,则由(16),(20)式及
可得
定理3得证.
由定理1-3以及引理1,可得如下定理4.
定理4若假设和成立,gk为算法V-WWP生成的序列,则
定理5若αk满足MWWP(δ1,δ,σ)条件,则αk也满足WWP(δ-δ1,σ)条件.
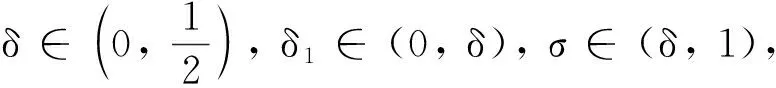
(21)
(22)
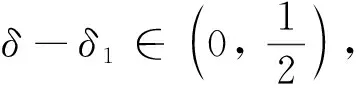
由定理5,类似定理4的证明过程,可得算法V-MWWP全局收敛,即如下定理6成立.
定理6若假设和成立,gk为算法V-MWWP生成的序列,则
4 数值实验
利用文献[19]的部分测试问题,维数分别取1 000,5 000,10 000,对算法PRP(采用MWWP搜索)和算法V-MWWP进行数值试验. 试验环境为:ThinkPad E580,Intel(R) Core(TM) i5-8250U CPU@1.60GHz,RAM 8.00GB,Windows 10,Matlab R2016a. 算法参数δ1=0.05,δ=0.1,σ=0.9,μ=5.1,ε=10-6. 终止条件为‖gk‖≤10-6或迭代次数N≥1 000. 计算结果见表1,其中t表示算法所耗CPU时间,NaN表示算法终止时未满足‖gk‖≤ε.
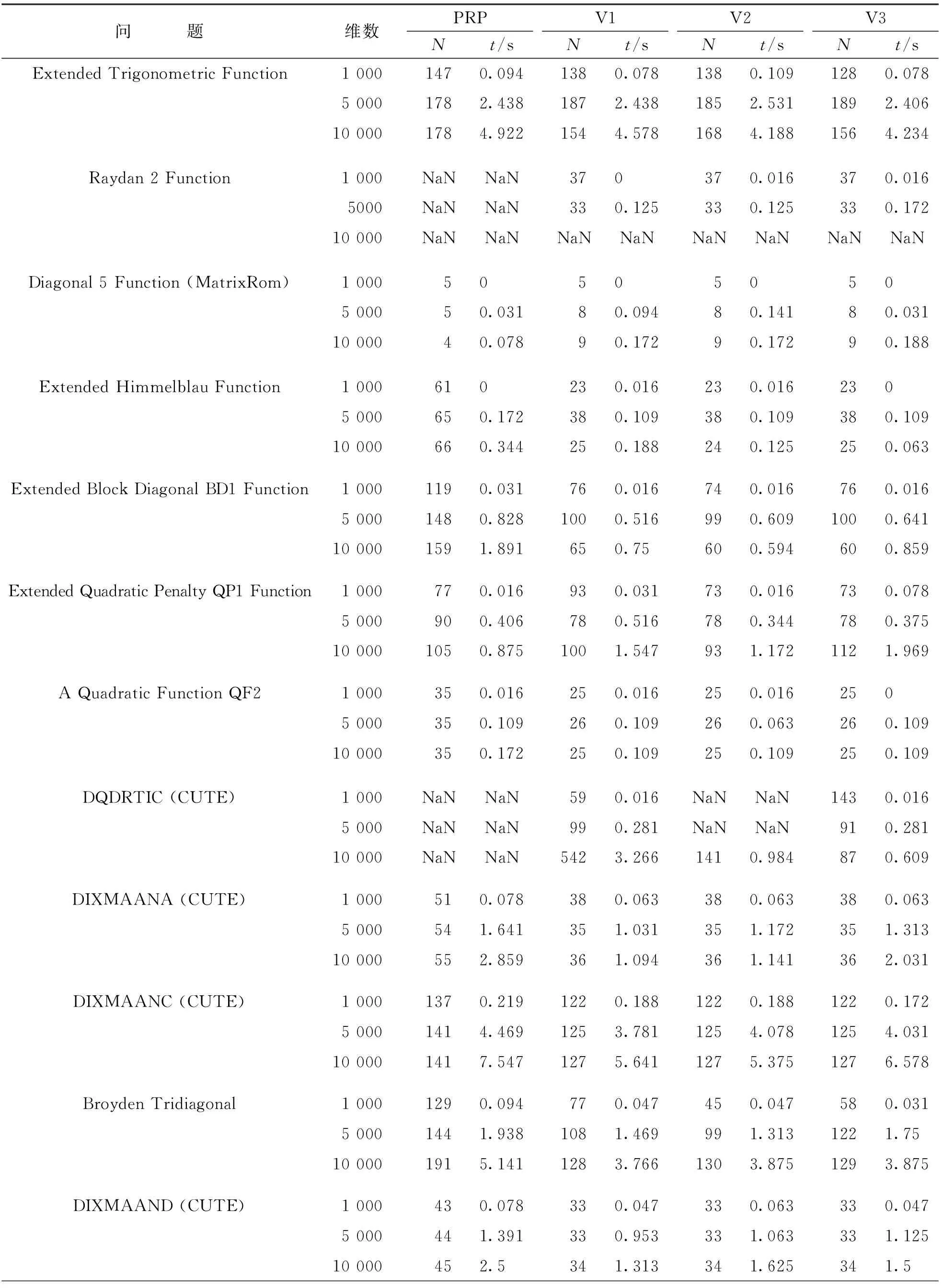
表1 数值结果
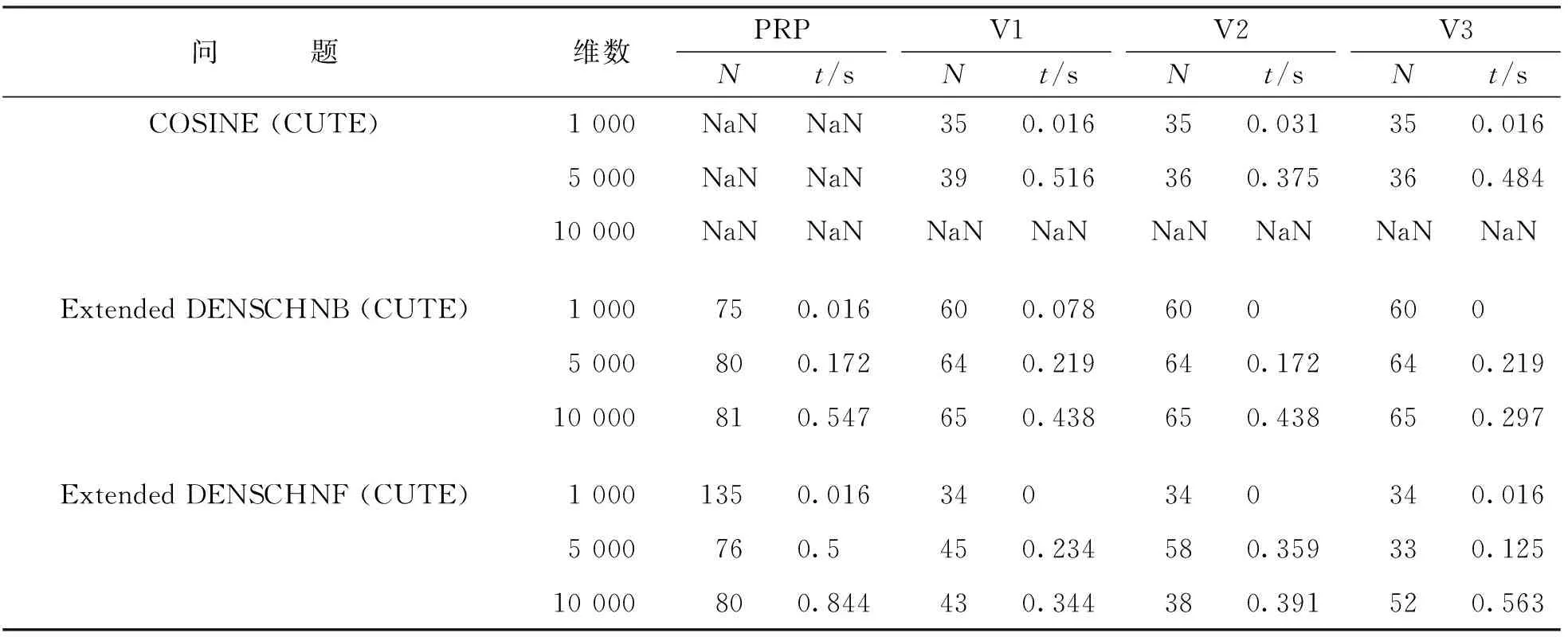
续表1
应用文献[20]的技术得到算法PRP与算法V关于迭代次数和CPU时间比较的效能图(图1和图2). 可见算法V对这些测试问题的数值表现比算法PRP更好些.
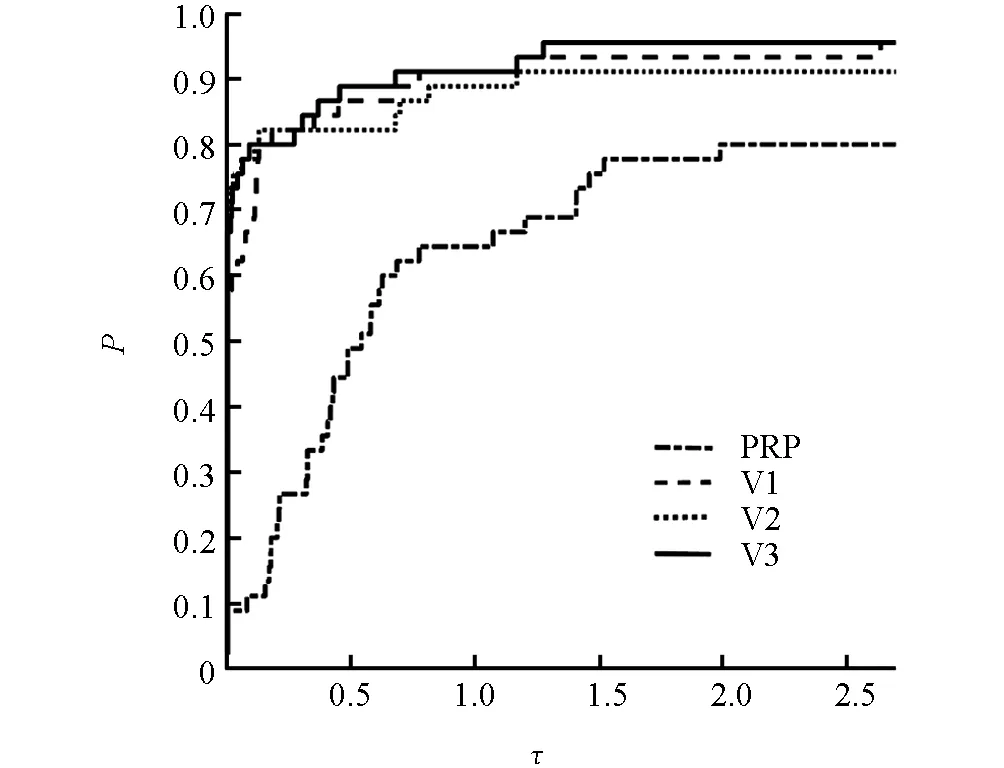
图1 算法迭代次数效能图
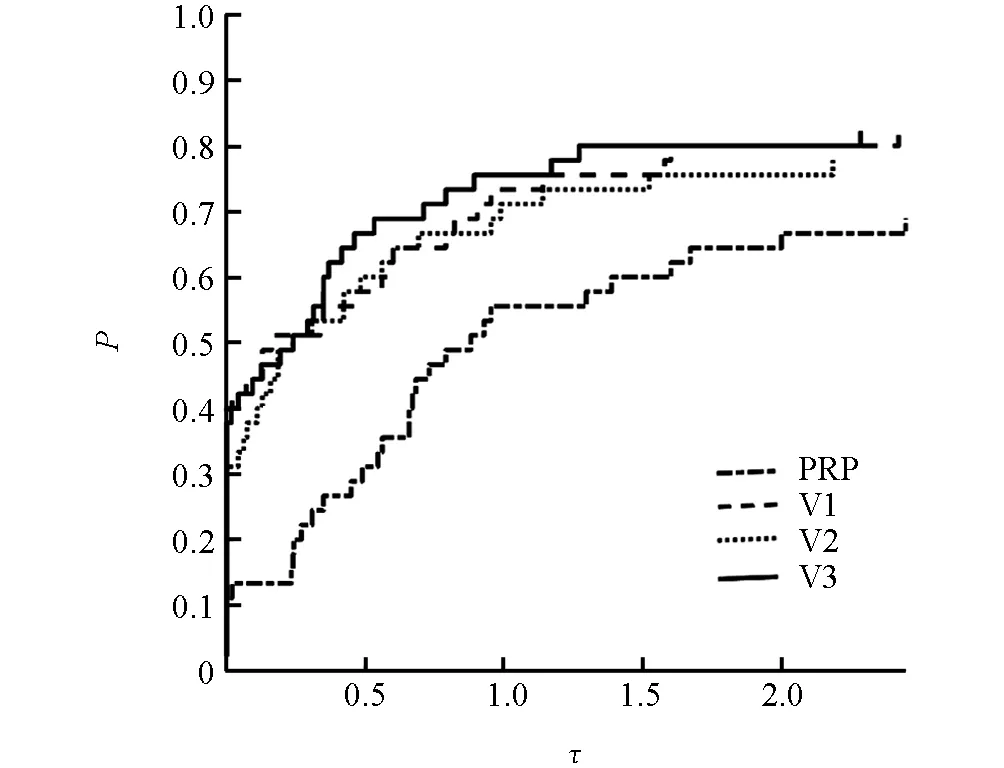
图2 算法CPU时间效能图
