基于弹性力学的钢桥面铺装层应力分析
2021-07-18裴智毅徐秀丽
裴智毅,吴 鹏,周 叮,徐秀丽
(1.无锡市政设计研究院有限公司,江苏 无锡 214072;2.南京工业大学 土木工程学院,江苏 南京 211800)
随着我国桥梁建设不断发展,钢箱梁桥桥面铺装的破损与开裂问题日益凸显。箱梁结构的复杂性,铺装类型与铺装材料的差异性均对钢箱梁桥桥面铺装层的内部力学状态产生重要影响[1-5]。因此研究钢箱梁桥桥面铺装的力学特性,建立考虑箱梁结构的铺装层应力计算模型,对分析桥面铺装的路用性能起着至关重要的作用。铺装层设计与钢箱梁结构设计是相互联系的,铺装层的应力状态取决于铺装层的厚度、模量组合及箱梁的结构特性[6-8]。
现阶段对桥面铺装的分析方法主要有实验法、有限元法及理论计算法。理论计算法主要采用叠层梁模型来计算桥面铺装的弯曲应力。胡长顺等[9]、王虎等[10-11]最早提出了基于梁体结构的桥面铺装层线弹性分析模型,并推导了活载作用下桥面铺装的弯曲正应力计算公式。张占军等[12]在其基础上采用叠加原理,分析了沥青混凝土铺装层及防水层的参数变化对混凝土桥桥面铺装层弯曲应力的影响。赵锋军等[13]基于叠层梁模型,提出了桥面沥青铺装层横桥向弯曲应力的实用计算公式,进一步分析了铺装层的力学特性。但以上桥面铺装计算理论均基于欧拉梁模型,忽略了剪切变形对铺装层应力的影响,存在一定误差。
通过分析钢箱梁桥桥面铺装的力学特性,结合二维弹性力学理论,尝试提出了考虑层间剪切变形的钢桥桥面铺装应力计算解析式。并在此基础上,进一步研究了车辆荷载作用下,铺装层厚度组合及横隔板截面尺寸变化对钢桥桥面铺装层应力及位移的影响。为钢箱梁桥桥面铺装设计的整体化、标准化、模块化提供理论依据。
1 桥面铺装层模型
以广东马房大桥STC桥面铺装[14]为例(图1)。分别计算在规范荷载及超重荷载作用下,铺装层的应力值。
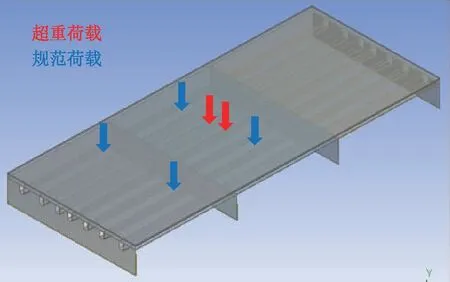
图1 钢-STC组合桥面模型Fig.1 Model of steel plate-STC composite structure
为研究STC桥面铺装层的应力状态,将横隔板看作支撑,将L形肋、钢桥面板、STC层以及磨耗层等效为层合梁模型 (图2)。铺装层等效截面模型[15]如图3所示,等效截面应力值是原截面应力值的bi倍(bi为各子层桥面横截面宽度)。
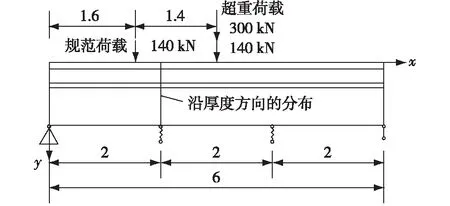
图2 STC铺装层模型(m)Fig.2 STC pavement layer model (m)
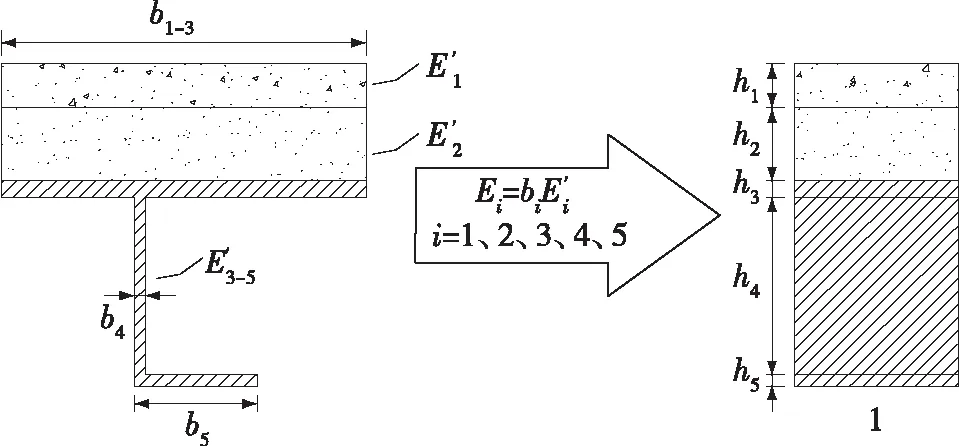
—原铺装层第i层结构弹性模量;—原铺装层第i层结构宽度;Ei—等效弹性模量;hi—第i层的厚度图3 铺装层等效截面模型Fig.3 Equivalent section model of pavement layer
2 应力与位移计算模型
计算假定:①各铺装层层间应力、变形连续;②桥面铺装材料均为各向同性材料;③桥面结构在横桥向的连接刚度视为无穷大。
2.1 基本方程
多跨层合梁平面应力计算模型如图4所示。

图4 多跨层合梁的平面应力计算模型Fig.4 Plane stress calculation model of multi-span beam
图4中梁长为l、层数为p、第i层的厚度为hi,h为层合梁总厚度,各层界面的竖向坐标为yi,弹性模量为Ei,泊松比为μi。图4(a)中采用整体坐标系(x-o-y)对整体层合梁进行分析,层合梁上表面作用任意竖向荷载q(x),下表面存在K′个弹性支座。采用整体坐标系(x-o-y)对整体层合梁进行分析,采用局部坐标系(x-oi-yi)对各子层进行分析[16]。
根据弹性力学平面应力模型,对第i层进行分析。由弹性力学本构方程[17]可得用位移表示的应力平衡微分方程:

(1)
式中ui、vi是第i层梁在x方向和y方向的变形。
对于简支层合梁,其边界条件满足下式:

(2)

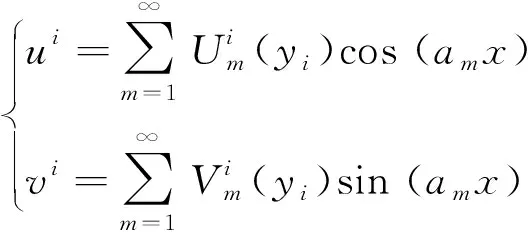
(3)
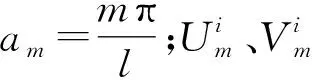
将式(3)代入式(1)中,可得第i层梁位移与应力分布的一般解析式。
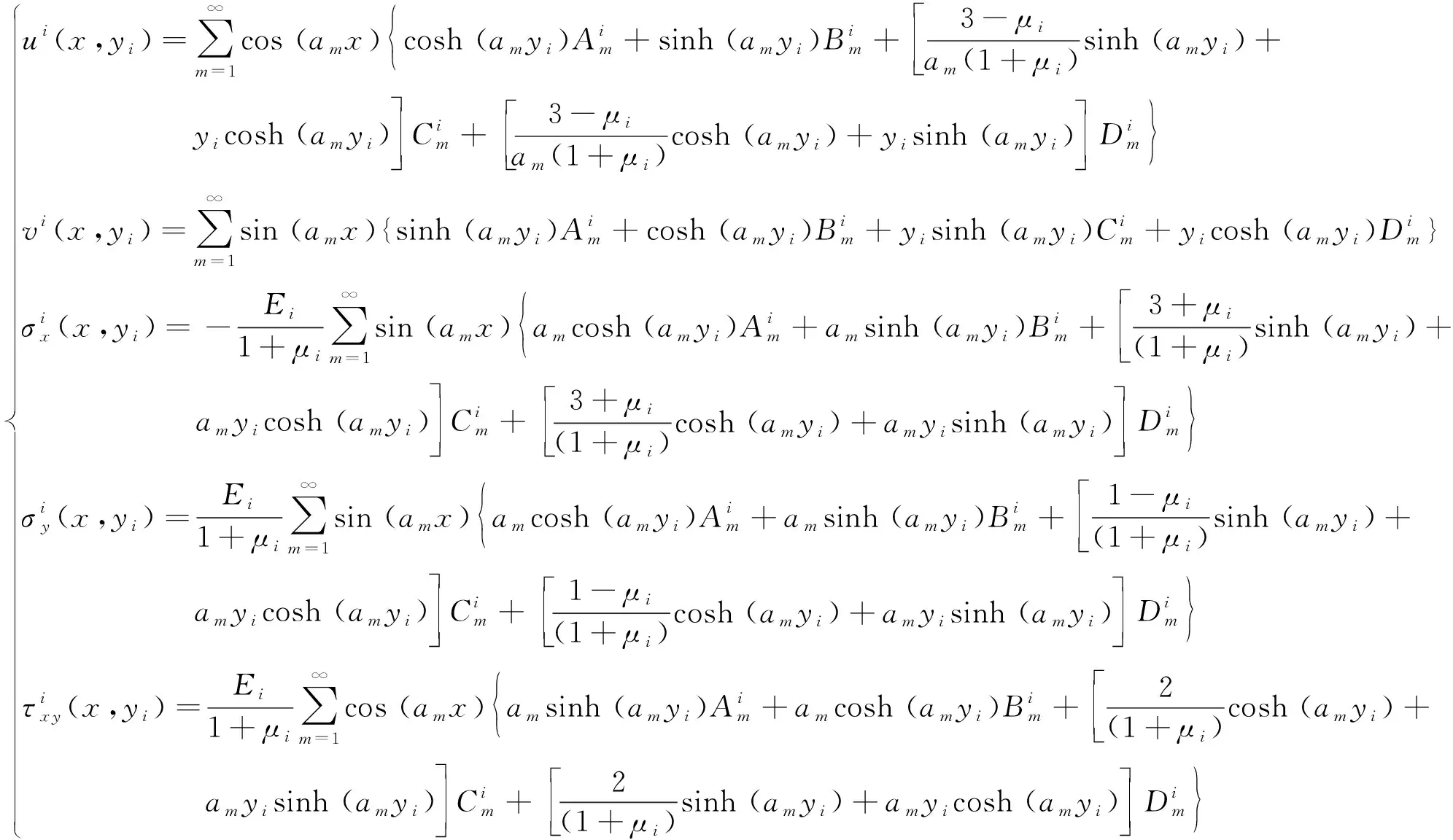
(4)
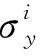
2.2 界面与上下表面边界条件
根据假设①可得,层间界面条件满足下式:
(5)
如图4中计算模型所示,层合梁模型上表面作用任意竖向荷载,故上表面边界条件满足下式:

(6)
式中q(x)为任意竖向荷载函数。
层合梁模型下表面存在竖向弹性支座,故将支座反力视为作用于梁底的未知力,建立支座力与支座位移之间的函数。
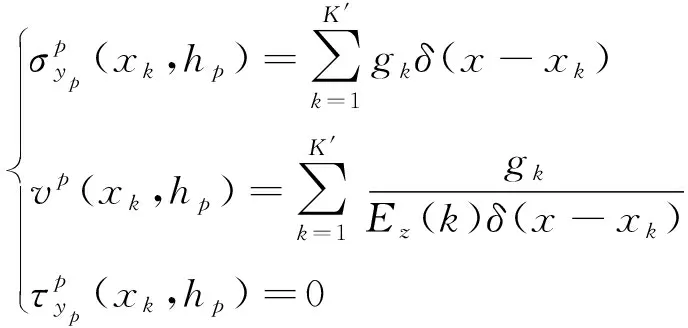
(7)
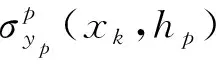
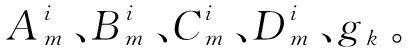
3 收敛性与比较研究
为研究本文算法的收敛性与合理性,本文以广东马房大桥STC桥面铺装新体系为例(有关参数见表1、2)。计算了在车辆荷载作用下桥面铺装模型顺桥向挠度值及桥面铺装沿厚度方向的应力值,并与文献值[14]、现场实测数据[19]以及有限元解进行对比分析。

表1 桥面结构几何参数Table 1 Geometric parameters of bridge deck

表2 材料物理力学参数Table 2 Physical and mechanical parameters of materials
对上表面作用超重汽车荷载的STC桥面铺装简化模型进行分析(图2)。计算在不同级数项截断时x=2 m、y=50 mm处的σx和x=0 mm、y=150 mm处的τxy,以判断本文位移、应力计算结果的收敛性(见表3)。由表3可得,当N=80时,本文解σx、τxy均已收敛。
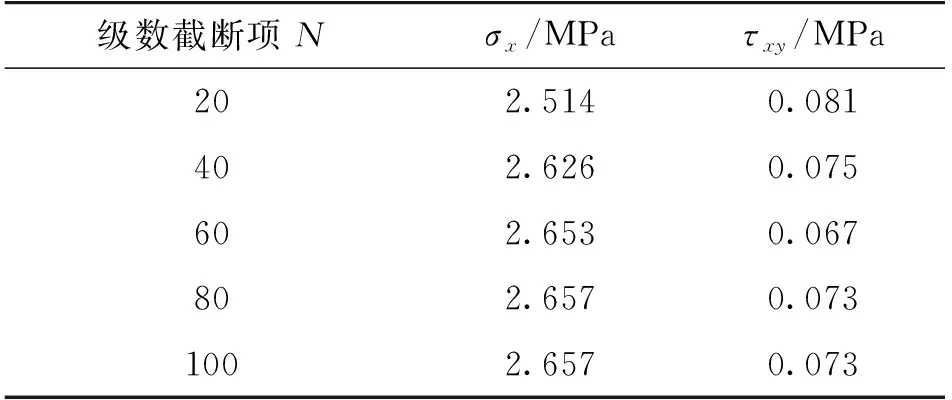
表3 应力收敛性Table 3 Convergence of stresses
采用本文计算模型计算STC桥面铺装沿顺桥向的挠度值,并与实桥实测挠度值[19]及文献值[14]进行对比,计算结果见表4。从表4中可以看出,本文计算挠度值略小于实测值,误差为2.41%,证明了本文计算结果的合理性。根据假设③,笔者采用二维平面计算模型,横向连接刚度视为无穷大,所以本文计算挠度值较文献值与实测值偏小。
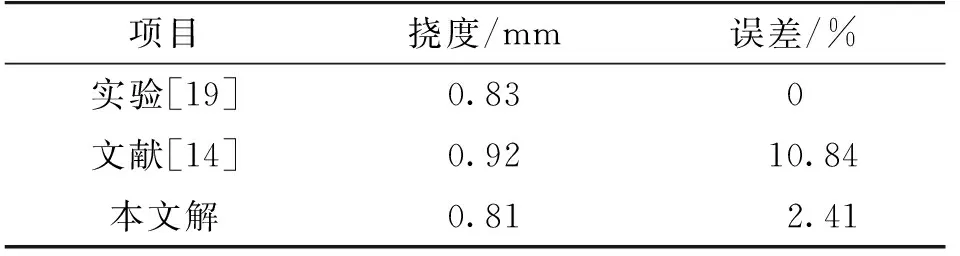
表4 误差分析Table 4 Error analysis
采用本文模型分别计算在规范荷载及超重荷载作用下,横隔板处铺装层应力沿厚度的分布状况,并与二维有限元解及文献值对比,结果如图5所示。从图5中可以看出,1)本文解与二维有限元解(plane183)吻合度高,与文献值间存在较大偏差。出现此类情况的原因在于文献值[14]采用的空间有限元模型对STC铺装层进行分析,轮载在横桥向分布不均,导致近轮载处隔板顶部铺装层的拉应力偏大,远离轮载处隔板顶部铺装层的拉应力偏小。而本文计算模型基于二维层合梁理论,横桥向刚度视为无穷大。在荷载作用下,隔板顶部拉应力在横桥向均匀分布,故本文解小于文献值[14]。2)本文解与文献值存在相同的变化规律。3)与超重荷载相比,在规范荷载作用下本文解与文献值吻合度更高。
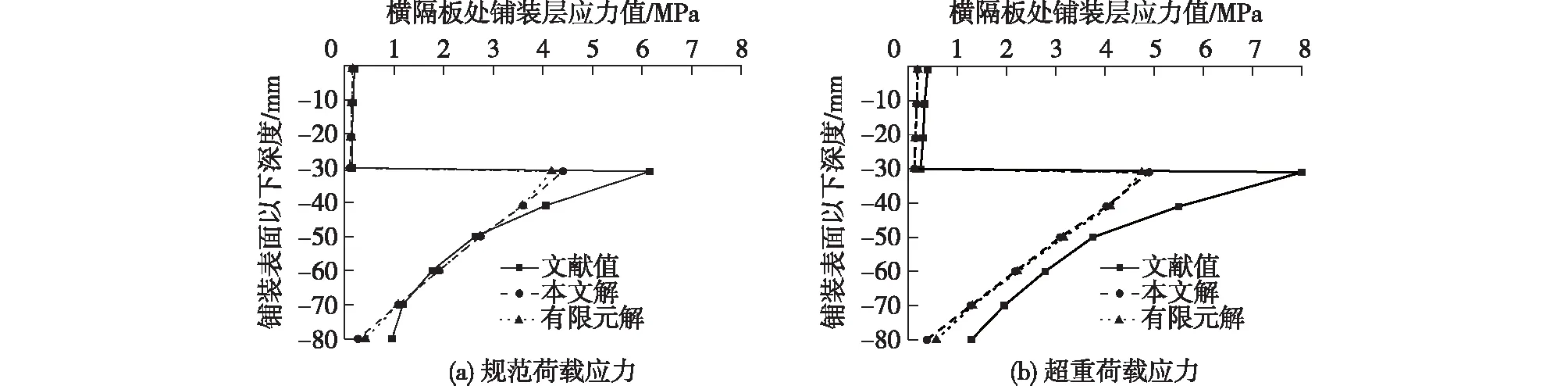
图5 铺装层应力沿厚度的分布Fig.5 Stress distribution of pavement along layer thickness
4 参数分析
4.1 铺装层各子层厚度对其应力影响
保持STC桥面铺装总厚度不变(80 mm),分别变化沥青层和STC层厚度。采用本文计算模型,分析不同厚度组合对桥面铺装应力的影响。
随着STC层厚度的减小,铺装层沿厚度方向的应力分布及其峰值变化规律如图6和表5所示。从图6中可以看出,横隔板处桥面铺装最大拉应力值随STC层厚度的减小而增大,最大拉应力位置逐渐下移。从表5中可以看出,拉应力最大变化值为0.152 MPa,最小变化值为0.063 MPa。随着STC层(高弹模层)厚度变小,应力变化速率呈下降趋势。综上可得,在铺装层总厚度确定时,适当增加高弹模层厚度能有效提高桥面结构刚度,减小铺装层最大应力值。
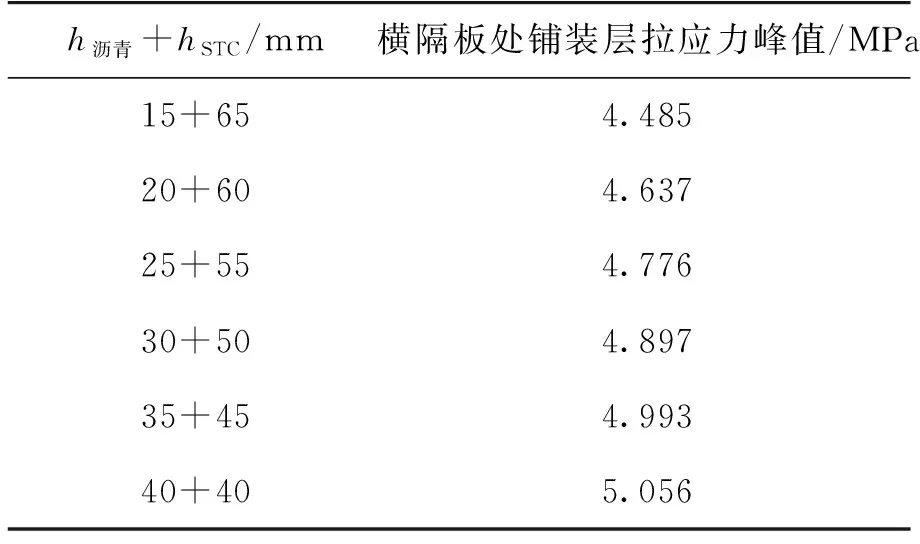
表5 不同厚度组合铺装层拉应力峰值Table 5 Maximum tensile stresses of pavement with different stiffnesses
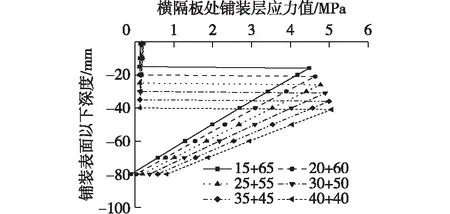
图6 不同厚度组合铺装层拉应力分布Fig.6 Tensile stress distribution of pavement under different stiffnesses
4.2 隔板刚度对铺装结构应力状态影响
通过改变横隔板腹板厚度,以研究其对铺装层应力状态的影响,支座刚度Ez(i)的等效公式为

(8)

在横隔板腹板厚度合理区间内[20](表6),分析其腹板厚度变化对桥面铺装应力分布的影响,见图7、8。从图7和8中可看出,随着横隔板腹板厚度的增加,横隔板处桥面铺装层最大拉应力呈对数递增,拉应力最大变化值为0.011 MPa,最小变化值为0.001 8 MPa。中跨跨中处铺装层的最大压应力呈指数递减。压应力最大变化值为0.010 8 MPa,压应力最小变化值为0.001 8 MPa。综上可得:1)横隔板腹板厚度的变化对铺装层应力影响较小;2)在横隔梁刚度和强度足够的条件下,适当减小横隔梁腹板厚度能降低铺装层结构横隔板处的拉应力水平。
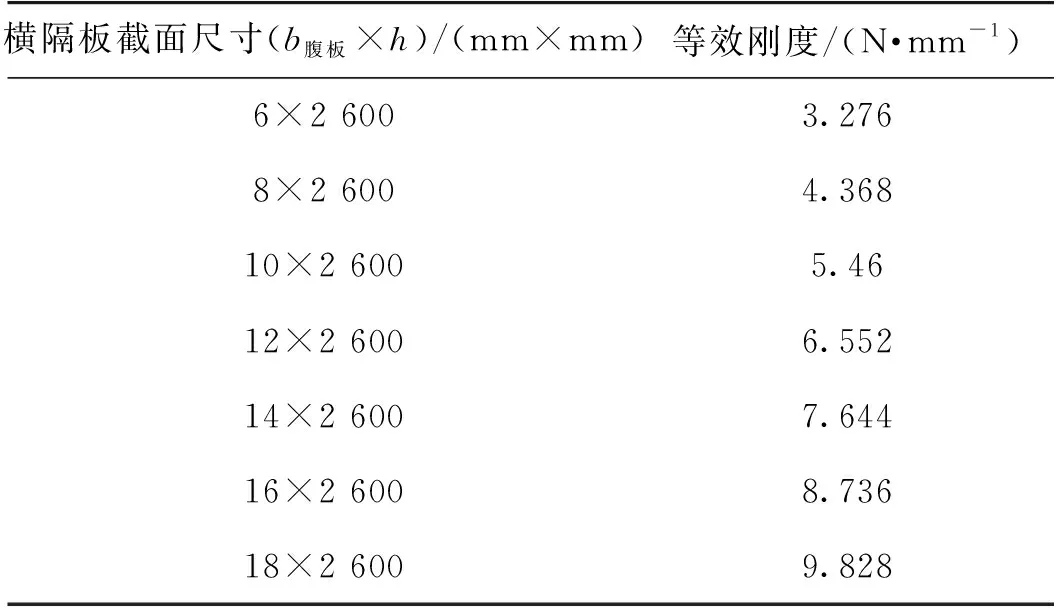
表6 横隔板尺寸及等效刚度Table 6 Diaphragm dimension and equivalent stiffness
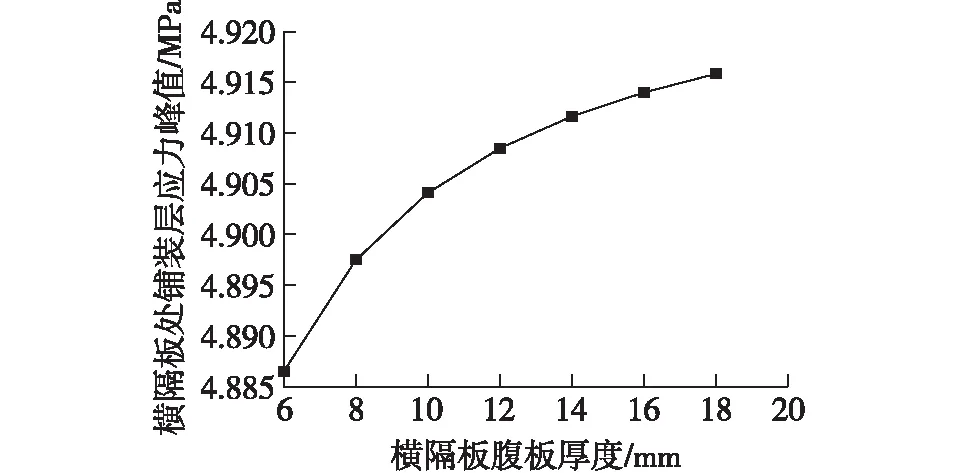
图7 不同腹板厚度铺装层拉应力峰值Fig.7 Maximum tensile stresses of pavement layer with different web thicknesses
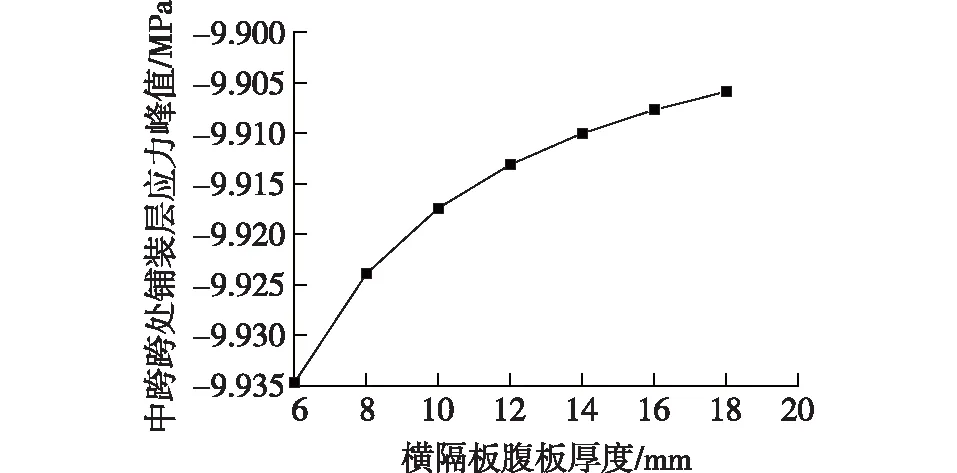
图8 不同腹板厚度铺装层压应力峰值Fig.8 Maximum compressive stresses of pavement layer with different web thicknesses
5 结论
1)在钢桥桥面铺装总厚度不变的情况下,适当增加桥面铺装高弹模子层(STC层)厚度,能有效提高桥面结构刚度,降低铺装层应力水平。
2)箱梁中横隔板腹板厚度的变化对桥面铺装应力存在一定影响。故在箱梁结构设计时,可根据铺装材料特性及结构设计需求对横隔板厚度合理取值。
3)针对STC桥面铺装新体系,提高铺装层组合模量较改变箱梁横隔板腹板厚度能更有效地改善钢箱梁桥面铺装层的力学性能。
