FP-Tree算法规则挖掘的研究与应用

王大勇，李 丽，张 蕾，孙时光

(1.辽宁大学创新创业学院，辽宁 沈阳 110036；2.东北师范大学物理学院，吉林 长春 130024)

0 引言

随着大数据时代的到来，对数据和数据之间的关联关系进行深度挖掘和处理就显得尤为重要，数据之间的关联关系是大数据中待挖掘的一类重要信息.关联是指变量的数值中有2个或2个以上存在一定的规律，可以通过关联分析挖掘出数据中的关联关系.关联分为简单关联、时序关联和因果关联.关联规则挖掘过程一般先从数据集合中找出所有的高频项目组，再由高频项目组产生关联规则.

1993年，Agrawal等首先提出了挖掘关联规则问题，并对顾客交易数据库中项集之间的关联规则挖掘问题进行研究，此后基于关联规则的挖掘问题的研究逐步推广，并吸引了大量的科研人员投入到该项研究中.关联规则挖掘是大数据研究的一个重要课题.目前，关联规则挖掘技术主要集中在金融行业以及电子商务中.

Apriori算法是一种挖掘布尔关联规则频繁项集的算法，广泛应用于多个领域中，包括商业金融、网络安全、高校管理、移动通讯等.Apriori算法的实现包括3个阶段：第1阶段利用递推方法找出所有的频集，这些项集出现的频繁性要大于等于预定义的最小支持度；第2阶段由频集产生强关联规则，这些规则必须满足最小支持度和最小可信度；第3阶段产生只包含集合项的所有规则.由该思想生成的规则均大于用户给定的最小可信度.

Apriori算法虽然是经典的规则挖掘算法，但在执行过程中可能产生大量的候选集，并可能出现重复扫描数据库的问题.针对Apriori算法的这些缺点，文献[1-3]提出了FP-Tree算法.FP-Tree算法的思想是构造一棵频繁模式树，把数据库中的数据映射到树上，这种频繁模式树简称为FP-Tree.通过两次扫描事务数据库把每个事务所包含的频集压缩到一棵FP-Tree中，此后只需通过FP-Tree进行查找，不需要再扫描事务数据库，避免了重复扫描数据库的问题.通过递归调用FP-Tree发现频繁模式的算法，可直接产生频繁模式，因此，该算法执行过程中也避免了大量候选集的产生.数据表明，FP-Tree算法在效率上比Apriori算法有显著的提高[4-7].

大学生所处的年龄阶段正值生长稳定期，各项生理功能处于成熟阶段，具备较强的机体免疫力，相比其他年龄阶段的人群患病率低.但由于近年来随着科技水平的提高，外卖行业的兴起等诸多因素，导致大学生使用手机电脑等电子产品的时间越来越长，不健康食品的摄入量过多，体育活动得不到重视等情况时有发生，使得一些慢性疾病在大学生群体中相比以往有所增多，例如肥胖、高血压、免疫力低下等情况正在逐年递增.国内许多高校医疗系统内存储着大量的学生体检数据，其中很多数据只是能进行简单的存储以及查询等功能，而不能发掘出这些数据之间潜在的关联关系并加以利用.因此本文采用FP-Tree算法对存储的数据进行关联规则挖掘，发现大学生群体中常见的各种慢性疾病，力求在早期敦促大学生养成良好的生活习惯、减少严重慢性疾病的发生.

1 FP-Tree算法

FP-Tree算法能够高效地解决Apriori算法中存在的问题.因此对FP-Tree算法的相关定义和算法进行了描述.

1.1 相关定义

定义1 关联规则：指有关联的规则，对于两个不相交的非空集合X和Y，如果有X→Y，就说X→Y是一条关联规则.关联规则的强度用支持度和置信度来描述.

定义2 支持度：关联规则X→Y的支持度(support)用support(X→Y)=|X∩Y|/|N|表示，其中X和Y为事务数据库中的集合，|X∩Y| 是X和Y同时出现的次数，|N|为事务数据库中集合的个数.

定义3 置信度(confidence)：关联规则X→Y的置信度(confidence)用confidence(X→Y) =|X∩Y|/|X| 表示，其中X和Y为事务数据库中的集合，|X∩Y| 是X和Y同时出现的次数，|X|是集合X出现的次数.

支持度是对关联规则重要性的衡量，支持度越大，表示这种关联规则越重要.置信度是对关联规则准确度的衡量.有些关联规则的支持度虽高，但置信度低，说明该关联规则准确度不够，不能采用；有些关联规则的置信度虽然很高，但是支持度低，说明该关联规则出现的机会很小，实用价值不大.在进行实际关联规则挖掘分析时，必须选择恰当的最小支持度阈值和最小置信度阈值.如果取值过低，则会发现大量无用的规则，不利于所需规则的发现和获取.如果取值过高，则可能得不到规则，或者得到的规则过少，导致所需规则不满足条件而没有被筛选出来.一般需要根据实际情况设定合适的阈值.

支持度和置信度越高，说明规则越强，关联规则挖掘就是挖掘出满足一定强度的规则.下面举例说明支持度与置信度的计算方法.

假设事务数据库如下：

AEFG

AFG

ABEFG

EFG

其中每行代表一个事务，事务由若干个不相同项目构成，任意几个项目的组合称为一个模式.该例中共有4个事务.

模式{A，F，G}在4个事务中共出现3次，即支持数为3，经计算得到支持度support为75%，支持数大于最小支持数minsupport的模式称为频繁模式(Frequent Partten).

以此类推，{F，G}的支持数为4，支持度为100%.{A}的支持数为3，支持度为75%.

Confidence({F，G}⟹{A})等于75%.Confidence({A}⟹{F，G})等于100%.

1.2 FP-Tree算法描述

输入：事务集合 List> transactions，

输出：频繁模式集合及相应的频数Map，Integer>FrequentPattens，

初始化：PostModel=[]，CPB=transactions，

void FPGrowth(List> CPB，List PostModel){

if CPB为空，

return

}.

CPB的全称是Conditional Pattern Base(条件模式基)，是算法在不同阶段的事务集合.统计CPB中每一个项目的个数，把个数小于最小支持数minSuport的项目删除掉，然后对于CPB中的每一条事务按项目个数降序排列.

由CPB构建FP-Tree，FP-Tree中包含了表头项headers，每一个header都指向了一个链表HeaderLinkList，链表中的每个元素都是FP-Tree上的一个节点，且节点名称与header.name相同.得到从FP-Tree的根节点到TreeNode的全路径path，把path作为一个事务添加到newCPB中，要重复添加TreeNode.count次.用java描述的具体代码如下：

for header in headers：

newPostModel=header.name+PostModel，

newCPB=[]，

for TreeNode in HeaderLinkList：

FPGrowth(newCPB，newPostModel).

2 规则挖掘应用

把大学生体检数据库中的数据进行相关处理，得到对应的事务数据库，再对事务数据库中的数据运用FP-Tree算法[8-11]，进而得到一些有价值的关联规则，为医生诊断提供辅助依据.

2.1 数据处理

体检表中的数据很多都是有噪声的，因此在使用之前应该进行预处理操作：

(1) 把体检表中与实验无关的个人信息如姓名、民族、出生日期、专业等信息全部过滤掉.

(2) 对字段进行处理，例如身高和体重这2个数据不能完全体现出是否肥胖，所以需要对其进行处理，这2个字段需转换为身体质量参数BMI，m(体重)(kg)/h2(身高)(m)，这样才能对规则的发现起到直接的帮助.

(3) 为了顺利把关系数据库转换为事务数据库，需要把原始数据表中的一些连续的数值型字段进行离散化处理.

(4) 以学生为单位，把学生所患慢性病用相应的编码代替，以达到每个字段只有一种信息的目的.

(5) 编写程序读取关系数据库，得到适用于数据挖掘的事务数据库[12-15]，如表1所示.在表1中ID代表某名学生，ITEM代表该名学生所患的慢性疾病，A，B，E等各代表某种慢性疾病.病情与编码对照如表2所示.

表1 慢性病事务

表2 病情编码对照

2.2 实现过程

在慢性病事务数据库中任意选取10个事务应用于FPGrowth函数，完整实现过程选取的10个事务：

ABCD

BEDF

BCD

ABCEDF

ACF

BCF

ACD

ABCGD

ABGD

EG

每行代表一个事务，事务由若干个不相同的项目构成.假设最小支持数minSuport=3，统计每一个项目出现的次数，把次数低于minSupport的项目删除掉，剩下的项目按出现的次数降序排列，得到F1{D：7B：7C：6A：6F：4}.

对于每一条事务，按照F1中的顺序重新排序，并且把不在F1中的内容删除.这样原来的事务集合成为：

DBCA

DBF

DBC

DBCAF

CAF

BCF

DCA

DBCA

DBA

上面的事务集合即为当前的CPB，当前的PostModel为空.开始构造FP-Tree，初始状态下FP-Tree为空，建立FP-Tree时逐条读入排序之后的数据集，按照排序后的顺序插入到FP-Tree中，排序靠前的节点是祖先节点，靠后的是子孙节点.如果有共同的祖先，则对应的共同祖先节点计数加1.直到所有的数据都插入到FP-Tree后，FP-Tree建立完成.由CPB构建FP-Tree的步骤为：

步骤1.插入第1条事务(D，B，C，A)，FP-Tree如图1所示.

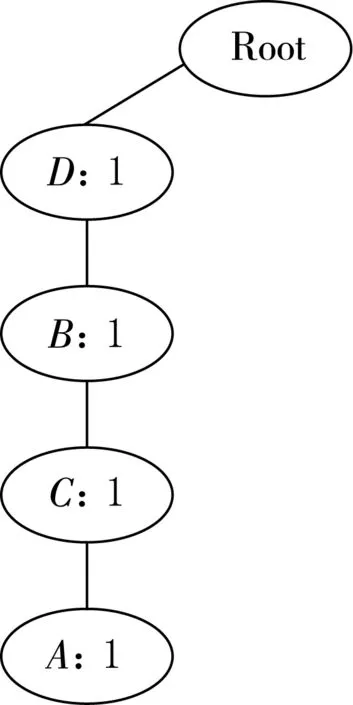
图1 插入第1条事务的FP-Tree

步骤2.插入第2条事务(D，B，F)，FP-Tree如图2所示.

图2 插入前两条事务的FP-Tree

步骤3.以此类推，把9条事务全部插入之后，得到图3所涉FP-Tree.

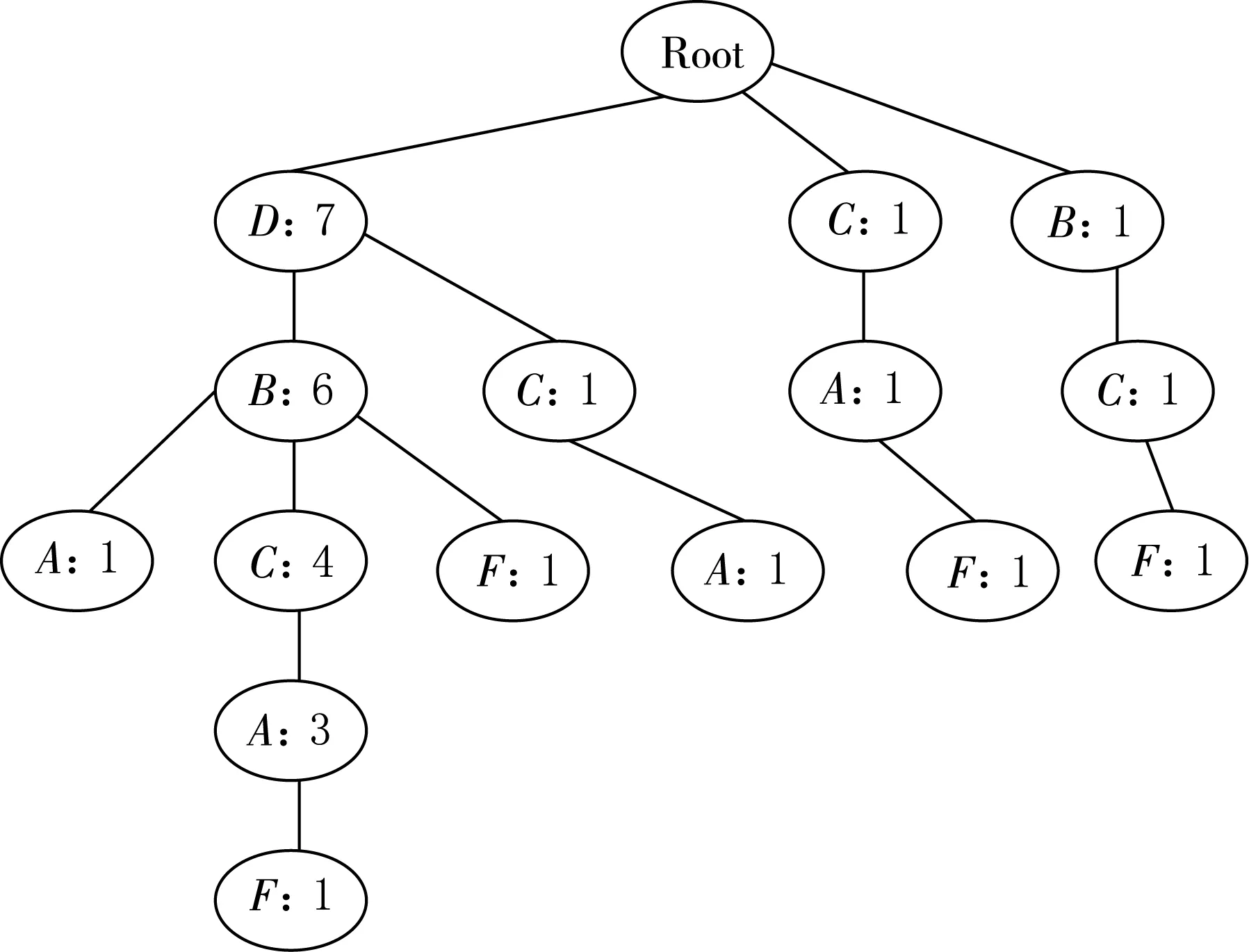
图3 插入全部事务的FP-Tree

另外建立表头项，表头项中记录的是频繁项集及其出现的个数.其次树中相同名称的节点要用链表链接起来，如图4所示，链表的第一个元素就是表头项里的元素.不论是表头项节点还是FP-Tree中的所有节点，它们都有2个属性：name(频繁项集的名称)和count(频繁项集的个数).

图4 用链表链接的FP-Tree

遍历表头项中的每一项，以“A：6”为例.

新的postModel为“表头项+原有postModel”，由于原有postModel的list为空，所以新的PostModel为[A].新的PostModel就是一条频繁模式，它对应的支持数即为表头项的count：6，所以此处可以输出一条频繁模式〈[A]，6〉.分为4个步骤.

步骤1.从表头项A开始，找到FP-Tree中所有的A节点，然后找到从树的根节点到A节点的路径.得到如下4条路径：

路径1：D：7，B：6，A：1；

路径2：D：7，B：6，C：4，A：3；

路径3：D：7，C：1，A：1；

路径4：C：1，A：1.

步骤2.对于每一条路径上的节点，其count都设置为A的count，结果如下：

D：1，B1：6，A：1；

D：3，B：3，C：3，A：3；

D：1，C：1，A：1；

C：1，A：1.

步骤3.因为每一项末尾都是A，可以把A去掉，得到新的CPB：

D：1，B1：6；

D：3，B：3，C：3；

D：1，C：1；

C：1.

步骤4.继续递归调用PFGrowth(新的CPB，新的PostMOdel)，当发现CPB为空时递归结束.

在FP-Tree是单枝的情况下，不需要再调用FPGrowth函数，直接输出路径上的各种组合+postModel即可.

3 实验结果

把事务数据库中的数据输入之后，得到输出结果如表3所示.

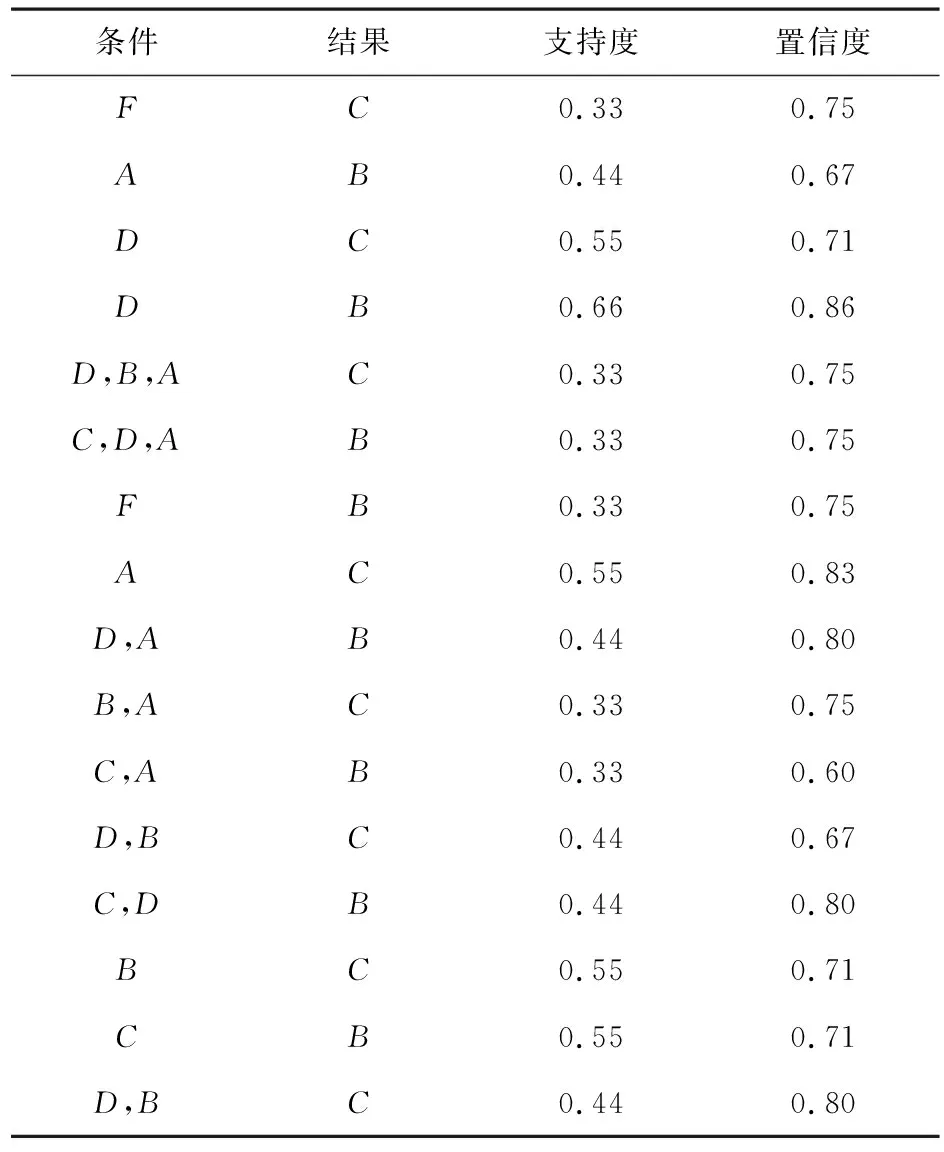
表3 测试样本输出结果

最小支持度阈值和最小置信度阈值一般由用户或领域专家设定，前者表示了规则的普遍程度，后者表示了规则的最低可靠度.支持度用于衡量关联规则的重要性或适用范围.置信度用于衡量关联规则的准确度，它反映了关联规则前提成立时其结果也成立的概率.

最小支持度与置信度阈值的设定对最终结果影响较大.如果最小支持度偏大，大量的潜在规则可能会被删除；相反，最小支持度偏小，则会推导出大量的规则，不便于决策者做出正确的判断.为使所挖掘到的关联规则具有一定的实用性.支持度阈值不宜设置过高，否则会遗漏重要的规则.本文针对大学生这一健康群体，同时患有多种慢性病的可能性较小，经过多次实验，设定最小支持度阈值和最小置信度阈值分别为10%和 50%，所获取的规则最符合医学常识.把学生体检表进行以上各种处理，对得到的事务数据库中的数据通过FP-Tree算法进行挖掘.产生的规则数目较多，在获取的规则中选取部分如表4所示.

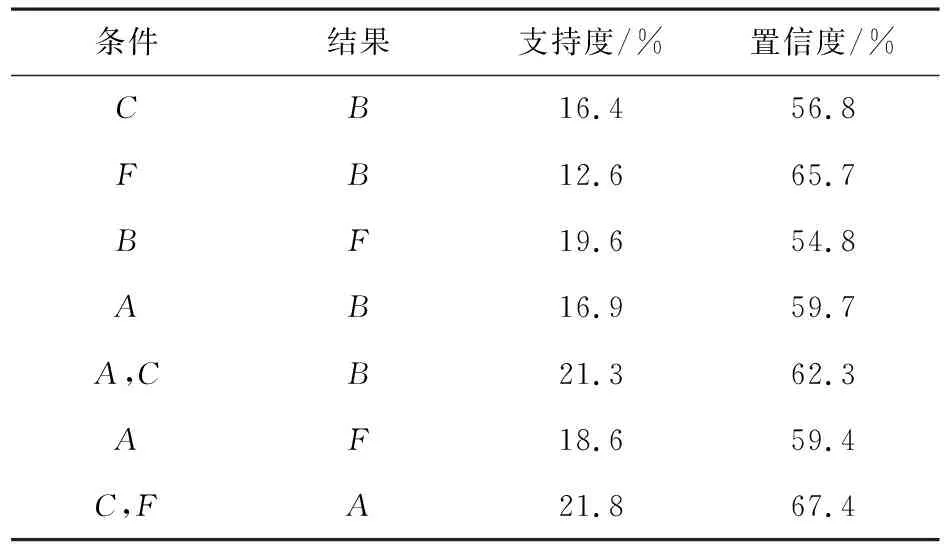
表4 慢性病之间的关联规则

4 结束语

本文对大学生体检数据库中的数据进行各种处理，得到便于进行数据挖掘的事务数据库.再将该事务数据库中的数据用FP-Tree算法进行处理，得到关联规则，经验证本文得到的规则是正确的且符合医学事实.在获取相关数据之后，可以及时告知学生患慢性疾病的风险，降低患病的概率，从整体上提高大学生这一群体的身体素质.