一类具多变时滞的高阶微分方程的Philos型准则
2021-07-17杨甲山
张 萍,杨甲山
(1.邵阳学院理学院,湖南 邵阳 422004; 2.梧州学院大数据与软件工程学院,广西 梧州 543002)
0 引言
振动性是微分方程有关理论的重要分支之一,它在自然科学和工程技术中有着广泛的应用,同时它也获得了学者们的广泛关注,并取得了许多研究成果[1-16].但关于同时具有阻尼项、正负系数、多变时滞及非线性中立项的n阶微分系统的研究却很少.考虑如下偶数阶微分方程的振动性:
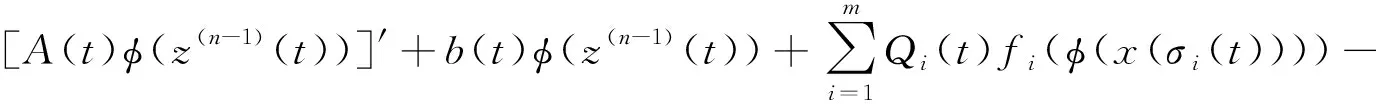
(1)

(H1) 函数A,Pk,b,Qi,Rj∈C([t0,+∞),[0,+∞)),k=1,2,…,h;i=1,2,…,m;j=1,2,…,l(下同,略).Bk,fi,gj∈C(R,R)并且uBk(u)>0(u≠0),ufi(u)>0(u≠0),ugj(u)>0(u≠0).

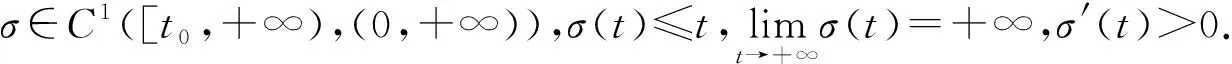
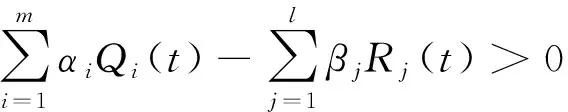
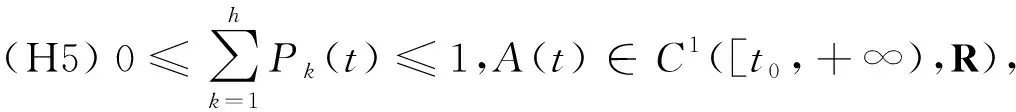
关于方程(1)的解及其振动性的定义,可参见文献[1-7,9-10,16].本文只讨论方程(1)的非平凡解.方程(1)包括了许多类型的微分方程,典型的如二阶Emden-Fowler型微分方程:
[A(t)|x′(t)|γ-1x′(t)]′+Q(t)|x(t)|γ-1x(t)=0,
(2)
{A(t)|[x(t)+p(t)x(τ(t))]′|β-1[x(t)+p(t)x(τ(t))]′}′+q(t)|x(δ(t))|γ-1x(δ(t))=0.
(3)
以及具有正负系数的二阶延迟微分方程:
{A(t)[x(t)+P(t)x(t-τ0)]′}′+Q(t)f(x(t-σ0))-R(t)g(x(t-δ0))=0,
(4)
(5)
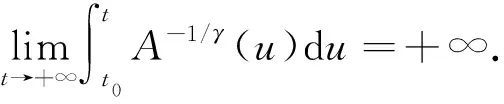
则方程(2)是振动的.
黄记洲等[3]则研究了二阶Emden-Fowler型微分方程(3)的振动性,并得到了该方程振动的Hille型如下振动准则:
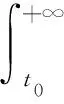
则方程(3)是振动的.
仉志余等[4]研究了具有正负系数的二阶微分方程(4)的振动性,主要结果如下:
定理C[4]设0≤P(t)<1,Q(t)≥0且R(t)最终为负.进一步,如果
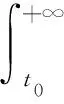
则方程(4)是振动的.
杨甲山等[5]则研究了较一般的具有正负系数的二阶微分方程(5)的振动性,进一步推广并改进了文献[4]的结果.而关于具有多变时滞和正负系数的n(n≥3)阶微分方程的振动性结果,目前还很少.本文将研究同时具有非线性中立项、阻尼项、正负系数及多变时滞的非线性偶数阶方程(1)的振动性,进一步改进、推广并拓展了现有文献中的研究成果.
1 几个引理
记
(6)
引理1[6]设u在[t0,+∞)上是正的n次可微函数,u(n)(t)最终定号,则存在t*≥t0和整数l(0≤l≤n),当u(n)(t)≥0时n+l为偶数,当u(n)(t)≤0时n+l为奇数,使得:当l>0时有u(k)(t)>0,t≥t*,k=0,1,…,l-1;当l≤n-1时有(-1)l+ku(k)(t)>0,t≥t*,k=l,l+1,…,n-1.
引理2[6]设u满足引理1的条件,且u(n-1)(t)u(n)(t)≤0(t≥t*),则对任何θ∈(0,1),存在常数M>0,使得对一切充分大的t有u′(θt)≥Mtn-2u(n-1)(t).
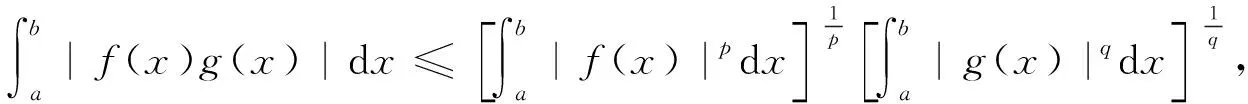
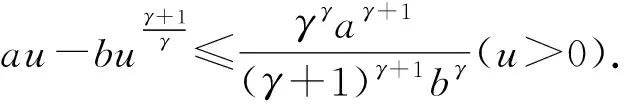
引理5 设条件(H1)—(H6)成立,x(t)是方程(1)的最终正解,则
z(t)>0,z′(t)>0,z(n-1)(t)>0,z(n)(t)≤0.
(7)
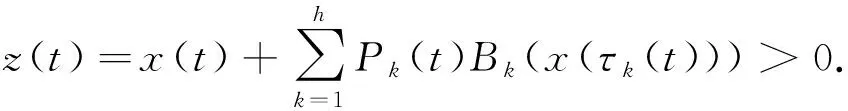
(8)
由(6)式知ω′(t)=ω(t)b(t)/A(t),所以
[ω(t)A(t)φ(z(n-1)(t))]′=ω(t){[A(t)φ(z(n-1)(t))]′+b(t)φ(z(n-1)(t))}<0.
(9)
因此ω(t)A(t)φ(z(n-1)(t))当t≥T时是严格递减的,且z(n-1)(t)最终定号.于是断言
z(n-1)(t)>0,t≥T.
(10)
若不然,即z(n-1)(t)<0,t≥T.由(9)式,得
ω(t)A(t)φ(z(n-1)(t))≤ω(T)A(T)φ(z(n-1)(T))=-C,
这里C=ω(T)A(T)[-φ(z(n-1)(T))]=ω(T)A(T)|z(n-1)(T)|γ-1[-z(n-1)(T)]>0是常数.于是由上式容易推得
两边积分,得
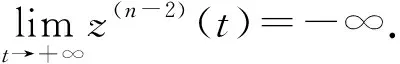
由(8)式,知
0≥[A(t)φ(z(n-1)(t))]′={A(t)[z(n-1)(t)]γ}′=A′(t)[z(n-1)(t)]γ+γA(t)[z(n-1)(t)]γ-1z(n)(t),
由此可导出z(n)(t)≤0(t≥T).由于n是偶数,因此由引理1知l为奇数,所以z′(t)>0(t≥T).引理5证毕.
2 主要结果及证明
记D={(t,s)|t≥s≥t0},D0={(t,s)|t>s≥t0},称二元函数H(t,s)属于函数类Θ,记为H∈Θ,如果二元函数H(t,s)∈C(D,R),且满足条件:
(ⅰ) 当t≥t0时H(t,t)=0,当(t,s)∈D0时H(t,s)>0;
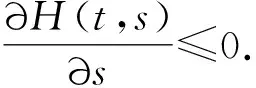
定理1 设条件(H1)—(H6)成立.若有函数φ∈C1([t0,+∞),(0,+∞))及H∈Θ,使得
(11)
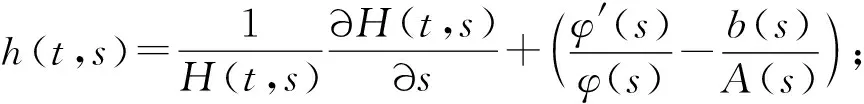
(12)
则方程(1)振动.
证明若不然,则方程(1)存在非振动解x(t),不失一般性,设x(t)>0,x(τk(t))>0,x(σ(t))>0,t≥T≥t0(若x(t)是最终负解时类似可证).由(7)式及引理2知,对任意0<θ<1,存在M>0,使得
z′(θσ(t))≥Mσn-2(t)z(n-1)(σ(t))≥Mσn-2(t)z(n-1)(t).
(13)
根据函数z(t)的定义,知x(t)≤z(t),因此
即
(14)
定义如下Riccati变换:
(15)
显然有V(t)>0(t≥T),应用(8),(13)和(14)式,由(15)式可推出
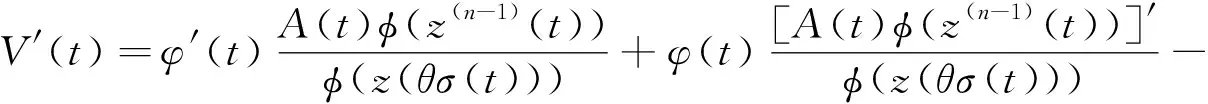
注意到(12)式中关于函数Φ(s)的定义,当t≥T时,由上式可得
(16)
将上式中的t改为s,再两边同乘以H(t,s)后积分,并注意到函数h(t,s)的定义,则可得到
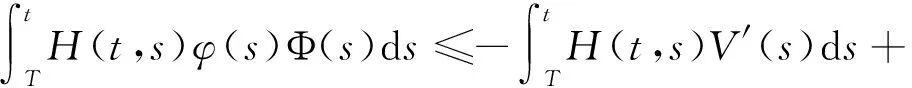
(17)
将引理4中的不等式应用于上式,并注意到函数ψ(s)的定义,则由(17)式进一步可得
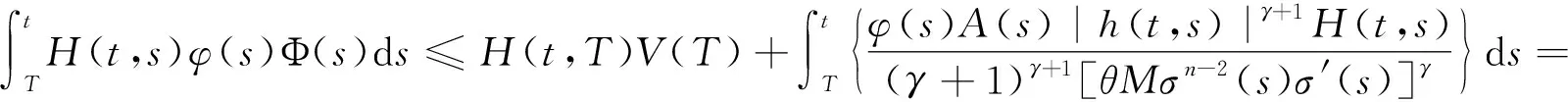
(18)
因此

(19)
从而
故


注1 如果方程(1)中的n=2,m=1,Pk(t)≡0,b(t)≡0,Rj(t)≡0,f(u)=u,σ(t)=t,并在定理1中取φ(t)=1,H(t,s)=(t-s)k,则由定理1可得定理A;如果方程(1)中m=1,Pk(t)≡0,Rj(t)≡0,fi(u)=u,则定理1即为文献[10]中的定理3;若取H(t,s)=(t-s)k,则进一步可得文献[10]中的定理1;如果方程(1)中n=2,h=m=l=1,b(t)≡0,γ=1,B(u)=u,τ(t)=t-τ0,σ(t)=t-σ0,δ(t)=t-δ0,则定理1即为方程(5)的振动准则,但定理1中放弃了文献[4]的条件“R(t)最终为负”.关于方程(1)的特殊情形的其他振动准则,可参考文献[6-9,11-16].
当定理1中的条件(11)不成立时,则有
定理2 设条件(H1)—(H6)成立.若有函数φ∈C1([t0,+∞),(0,+∞)),H∈Θ及ζ∈L2([t0,+∞),R),使得
(20)
(21)
对一切u≥T≥t0成立,并且函数ζ满足
(22)
其中函数Φ(s),ψ(s)及h(t,s)的定义如定理1,则方程(1)振动.
证明同定理1的证明,得到(17),(19)两式.由(19)式知,当t≥u≥T≥t0时,有
综合上式和(21)式,可得
(23)
根据(17)式,有
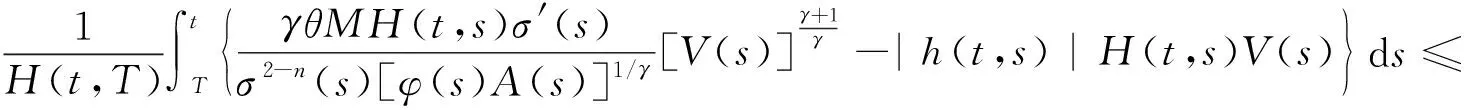
利用(23)式,由上式可推得
(24)
其中常数C0=-ζ(T)+V(T).由此可导出
(25)
(26)
这样,由(24)式可推出
(27)
综合(24),(26)—(27)式知,存在充分大的自然数N,使得当n≥N时,有
于是,对正数0<ε<1,当n≥N时,容易导出
(28)
利用引理3(即Hölder不等式),并注意到函数ψ(s)的定义,可推得
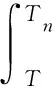
整理上式,并注意到(28)式及条件(20),则有
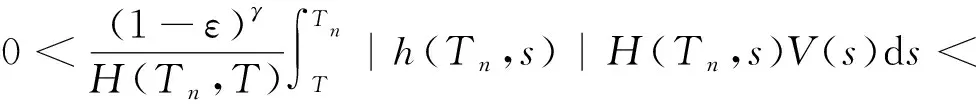
即
这与(27)式矛盾!这就证明了(25)式成立.利用(23)式的第1个式子及(25)式,可得
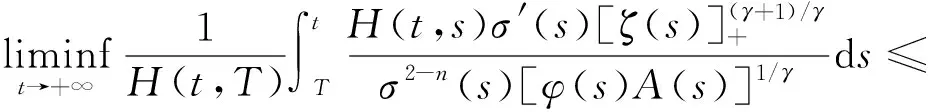
这与条件(22)矛盾!定理2证毕.
例1 考虑具有正负系数的4阶变时滞微分方程
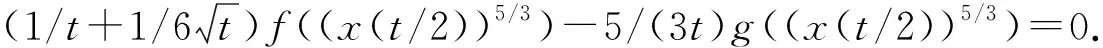
(29)
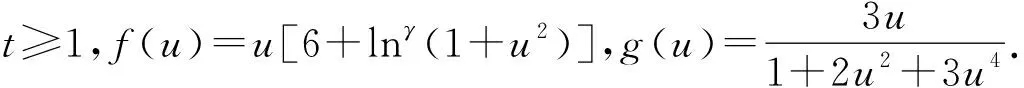
且当t→+∞时,有
所以条件(H1)—(H6)成立.现取φ(t)=1,H(t,s)=t-s,则当t→+∞时,有

于是由定理1知方程(29)振动.
显然,由于方程(29)的复杂性且是高阶(4阶)的,文献[1-16]中的定理均不能用于方程(29)的振动性判别.
