连续全场数字图像相关的反向组合高斯－牛顿算法*

卢 宇，陈 果，申 远，陈晓婷

(合肥师范学院电子信息与电气工程学院，安徽 合肥230601)

数字图像相关(Digital Image Correlation，DIC)[1－3]技术是一种广泛应用于位移和变形测量的非接触图像测量方法，是材料科学领域一种流行而有效的方法[4－6]。基于2D或3D-DIC技术的视频引伸计使用CCD摄像机拍摄试样表面散斑的全场位移与变形[7－9]。

DIC算法是由Peter[10]和Yamaguchi[11]分别在20世纪80年代提出的。对DIC算法的研究主要集中在算法的准确性和效率[12－13]。DIC算法按精度可分为整数像素法和亚像素法。整数像素算法采用零均值归一化互相关(zero-mean nomalized cross-correlation，ZNCC)[14－15]准则。相关系数的最大或最小峰值位置即为最佳配准点。为了提高ZNCC算法的计算效率，Lewis[15]在计算过程中引入了求和表和快速傅立叶变换，提出了快速零均值归一化互相关(fast zero-mean nomalized cross-correlation，FZNCC)。

为了提高配准精度，研究人员在不增加相机和镜头成本的前提下，提出了各种亚像素配准方法。这些方法包括相关系数拟合法和图像灰度梯度下降法。其中灰度梯度下降法比相关系数拟合法更适合于图像变形的测量[16]，也是DIC的标准方法。前向加性牛顿－拉弗森(forward additive Newton-Raphson，FANR)[17]算法是第一个提出来的梯度下降算法，目前已成为DIC技术中应用最广泛的算法。然而，FANR算法必须计算两个图像子集的相似度，并在每个迭代步骤中计算海森矩阵。这样的过程往往很耗时。Baker等人[18]提出了反向组合高斯－牛顿(inverse composition Gauss-Newton，IC-GN)算法，该算法比FA-NR算法效率更高，并获得了几乎一致的精度。IC-GN算法是当前DIC研究的热点之一[19]。然而，IC-GN算法在提出时只考虑了单点图像配准。为了进行全场图像变形测量，Pan等人[20]提出了双立方插值系数缓存表和初始值转移策略来加速全场配准计算的效率。Lu等人[21]提出了亚像素拟合初始值策略和子区域图像边缘扩展插值方法。这些方法提高了两幅图像全场配准的精度和效率。但是，在材料的力学性能测试过程中，CCD摄像机通常会获取数百、上千幅试样的图像。如果采用上述全场图像配准方式，则图像序列中每幅变形图像都必须与参考(未变形)图像进行配准，并且每次配准过程都需要计算参考图像中每个子区域的海森矩阵。这个过程消耗了大量的计算时间。因此，本研究提出了一种连续的全场图像配准方法，将海森矩阵缓存在缓存表中，以提高实际工程应用的效率。

本文首先介绍了传统的基于ZNCC和IC-GN算法的全场变形测量算法。随后，在基于双立方插值系数缓存表的 IC-GN(IC-GN with Bicubic interpolation coefficient cache table，IC-GN_BICCT)算法[20]的基础上又将海森矩阵缓存到IC-GN算法中，形成了基于双立方插值系数缓存表和海森矩阵缓存表的IC-GN(IC-GN with Bicubic interpolation coefficient cache table and Hessian matrix cache table，ICGN_BIC_HMCT)算法，以缩短后续图像的配准时间。通过对计算机生成的人工模拟散斑图像和CCD摄像机采集的真实散斑图像进行实验，验证了本文提出的基于算法有效性和准确性。结果表明，该算法可以在不损失精度的情况下提高IC-GN_BICCT算法的效率。

1 数字图像相关方法测量散斑图像变形的原理

2D-DIC技术被应用于材料力学性能测试实验中。在被测试样表面喷涂上黑白散斑并使用万能材料试验机拉伸，与此同时CCD摄像机采集散斑的平移和变形图像，可以通过这些图像来计算试样的位移和变形。试样拉伸前采集的图像称为参考图像，拉伸后的图像称为变形图像。图1给出了用视频引伸计测量材料力学性能的实验装置示意图。该系统由高分辨率定焦镜头、CCD摄像机、万能材料试验机、单色光源和高性能计算机组成。测试前被测试样固定在万能材料试验机的夹具上。CCD摄像机的光轴应尽可能垂直于试样表面。

图1 材料力学性能测量实验装置示意图

1.1 从粗到细的数字图像相关方法

图2 为CCD摄像机采集到的真实散斑图像。通常在图2(a)参考图像中选取一块尺寸为(2n＋1)×(2n＋1)像素尺寸的参考子区域，该子区域中心坐标为Pref(xref_c，yref_c)，与之对应的来自于变形图像的变形子区域的中心坐标为Pcur(xcur_c，ycur_c)，如图2(b)所示。为了找到配准点Pcur，可根据经验在变形图像中划出一个尺寸为(M×N)像素的搜索区域，然后使用由粗到细的方法搜索出Pcur。

图2 图像配准策略

ZNCC算法用于确定整像素精度级别的最佳配准点。ZNCC计算公式如式(1)所示[15]:

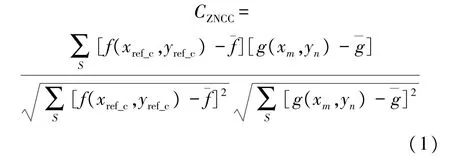
式中:g(x m，y n)表示以(x m，y n)为中心的变形子区域的图像灰度分布，(x m，y n)∈(M×N)。¯f和¯g分别为参考子区域和变形子区域的平均灰度值。S表示遍历子区域中所有的像素。ZNCC算法的优点是消除了背景光强度变化对配准的影响，而FZNCC算法通常用于提高ZNCC算法的计算效率。通过找到最大值CZNCC来确定变形子集在搜索区域中的位置(xcur_int，ycur_int)。

然而，ZNCC法只能获得位移而不能获得变形。在亚像素图像配准中，基于零均值归一化误差平方和准则(zero-mean normalized sum of squared difference，ZNSSD)的IC-GN算法是一种常用的亚像素配准方法。在说明IC-GN算法前，首先需要引入形函数W来描述参考子区域与变形子区域的对应像素位置关系:

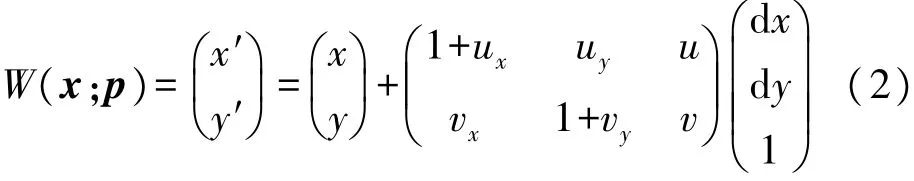
式中:p＝{u，v，u x，u y，vx，v y}T是2D仿射变换向量，其由6个独立的参数组成并定义了三种线性变换(即平移、剪切和缩放)。x＝(x，y)表示参考子区域内的像素坐标，(x′，y′)表示变形子区域内的像素坐标。另外，dx＝x－xref_c，dy＝y－yref_c。dx和dy的取值范围是－n≤dx，dy≤n。CZNCC的最大值坐标为(xcur_int，ycur_int)作为p中(u，v)的初始值。

基于ZNSSD的IC-GN算法可以表示为[12]:

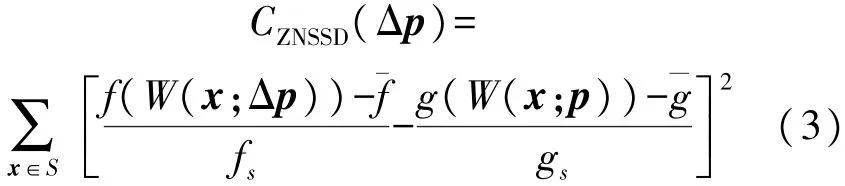
式中:Δp是p的增量。式(3)中

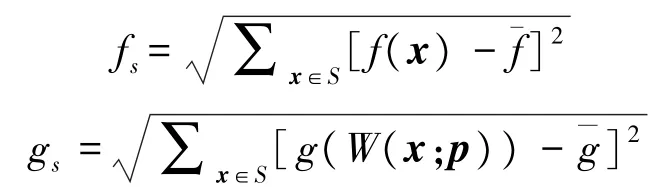
式(3)的解为:

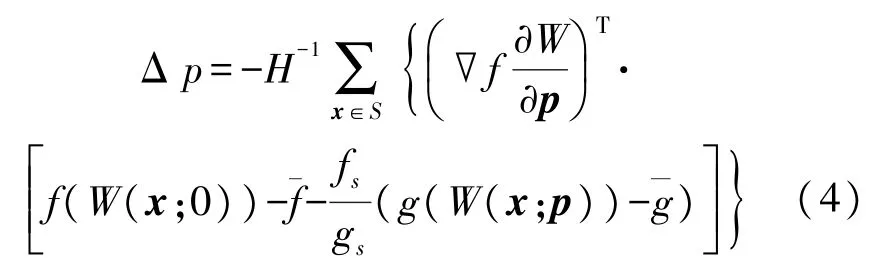
因此，Δp＝{Δu，Δv，Δu x，Δu y，Δv x，Δv y}T可通过式(4)得到。式(4)中的海森矩阵可以描述为:

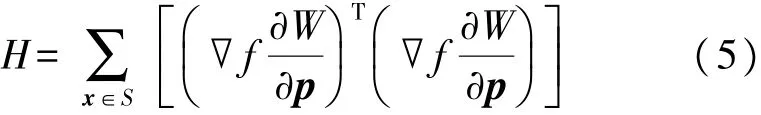
式中:∇f＝((∂f/∂x)，(∂f/∂y))是参考子区域的灰度梯度，∂W/∂p表示式(2)中对p求偏导:

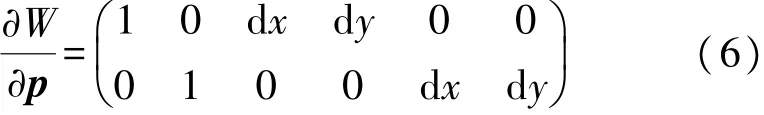
上述算法过程即为由粗到细，由整像素到亚像素的数字图像相关算法，可以简单表示为FZNCC＋IC-GN。

1.2 基于双立方插值系数缓存表和海森矩阵缓存表的IC-GN算法

在本节中，我们将IC-GN_BICCT算法引入到连续帧图像配准过程中。在式(4)中，参考子区域的∇f·(∂W/∂p)、H、H－1都需要计算，而且计算过程非常耗时。对于连续的图像配准，采取的配准策略往往如图3所示。第1步使用变形图像1与参考图像配准，第2步使用变形图像2与参考图像配准，以此类推。如果式(4)中参考图像的海森矩阵缓存表可以在后续图像配准过程中重复使用，则计算时间将大大减少。

图3 连续数字图像相关计算的示意图

全场配准计算时，需要在参考图像中选取被测区域，即感兴趣区域(RoI)。为了减少计算量，一般不会计算RoI中的所有像素点的位移与变形情况，而是在图像上设置具有固定间隔的网格，只计算网格上的种子点的位移与变形。

根据IC-GN_BICCT的步骤，使用IC-GN_BIC_HMCT算法计算连续全场数字图像相关的步骤如下:

(1)整个计算过程的预计算:

①在参考图像中选择出要计算的种子点矩阵的像素坐标；

②建立参考图像的二维海森矩阵缓存表M H，其行列数与种子点矩阵行列数相同；

③计算参考图像的∇f，¯f，f s；

(2)每幅变形图像的预计算:

建立变形图像的二维插值系数缓存表M c，其行列数与种子点矩阵行列数相同；

(3)每个参考子区域的预计算:

①根据式(5)计算种子点的H及H－1；

②如果是首次计算H及H－1，将H－1存入缓存表M H；否则在M H中查询；

(4)每幅图像的迭代:

①如果是首次计算插值系数，将系数存入缓存表M c；否则在M c中查询；

②使用形函数W(x；p)和M c计算g(W(x；

⑤使用式(4)计算Δp；

⑥更新W(x；p)←W(x；p)W(x；Δp)－1直至‖且ε＝10－3；

在IC-GN_BIC_HMCT算法步骤中(1)②、(3)①、(3)②是较IC-GN_BICCT算法增加的步骤。

2 实验和分析

本节利用计算机生成的人工模拟散斑图像和CCD摄像机采集的真实散斑图像，对比了IC-GN_BIC_HMCT算法和IC-GN_BICCT算法的计算效率。这两种算法的初始值均来自式(1)的ZNCC算法。

实验的硬件条件为4.0 GHz的Intel Core i3－8350K CPU，16 GB内存的台式机。IC-GN_BIC_HMCT、IC-GN_BICCT和IC-GN、FZNCC算法都用C＋＋和OpenCV库编写的。

2.1 使用人工模拟散斑图像的验证

我们首先使用一组来自实验力学学会(SEM)的2D-DIC challenge数据集[22]的散斑图像来验证本文所提出的算法的计算效率。其中来自该数据集的Sample 1是由一组具有恒定噪声数值的人工模拟散斑图像组成。图像的尺寸为512×512像素，灰度阶数为8位，灰度值的标准偏差为1.5。Sample 1使用TexGen[23]方法生成。Sample 1中的图像在X和Y方向上同时移动，范围从0像素到1像素，两幅连续图像之间的移动增量为0.05像素。Sample 1中有21幅图像，并且这些图像的对比度逐级下降。测试时，Sample 1的第1幅图像被视为参考图像。

在参考图像中选取从点(100，100)到点(400，400)的RoI用于计算，如图4的矩形区域所示。为了减少计算量，在X和Y方向上每隔10个像素选取1个种子点。因此RoI中共有961个种子点。

图4 Sample 1中的参考图像和RoI

为了定量研究IC-GN_BIC_HMCT和IC-GN_BICCT算法的误差，我们使用了如下的平均误差精度标准:

式中:N表示需要计算的种子点数量，u i，j为计算得到的参考图像中坐标为(i，j)的种子点的位移量，upreset是预设值.

使用包括参考图像在内的21幅连续图像与参考图像来计算全场位移并记录误差，结果如图5所示。图中分别使用尺寸为21×21、31×31、41×41像素大小的子区域。由于这两种算法的原理是相同的，所以两种算法的平均误差曲线是重叠的。图中可见两种算法的最大平均误差接近0.01像素，但对比度的变化不影响测量精度。图5中只给出了X方向位移的误差曲线。

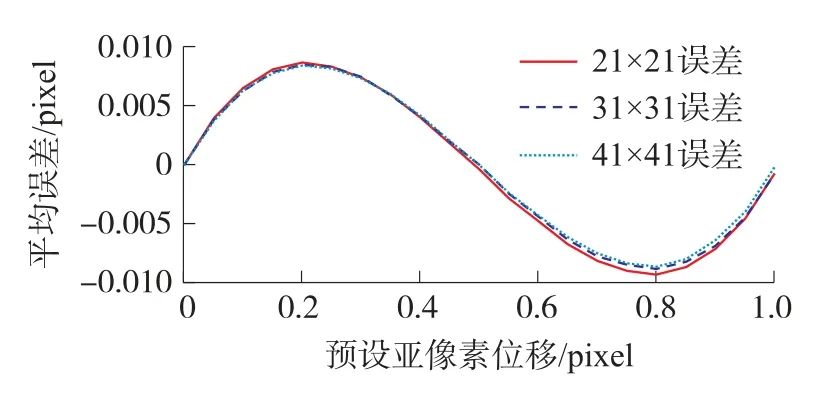
图5 Sample 1的IC-GN_BIC_HMCT和IC-GN_BICCT算法全场位移平均误差曲线

下一步是比较计算时间。图6给出了使用不同尺寸子区域的IC-GN_BIC_HMCT和IC-GN_BICCT的计算时间。在图6(a)、(b)、(c)中除第1个数据点外，IC-GN_BIC_HMCT的计算时间明显短于ICGN_BICCT。使用21×21尺寸子区域的IC-GN_BICCT的总时间为7.50 s，平均每幅图像为0.36 s。而IC-GN_BIC_HMCT的总时间为6.66 s，平均每幅图像为0.32 s。后者的效率比前者高11.35%。图6(a)、(b)、(c)中的第1个数据点，IC-GN_BIC_HMCT消耗的时间略长于IC-GN_BICCT的算法。这是因为IC-GN_BIC_HMCT算法有数据缓存步骤，消耗更多存储时间。

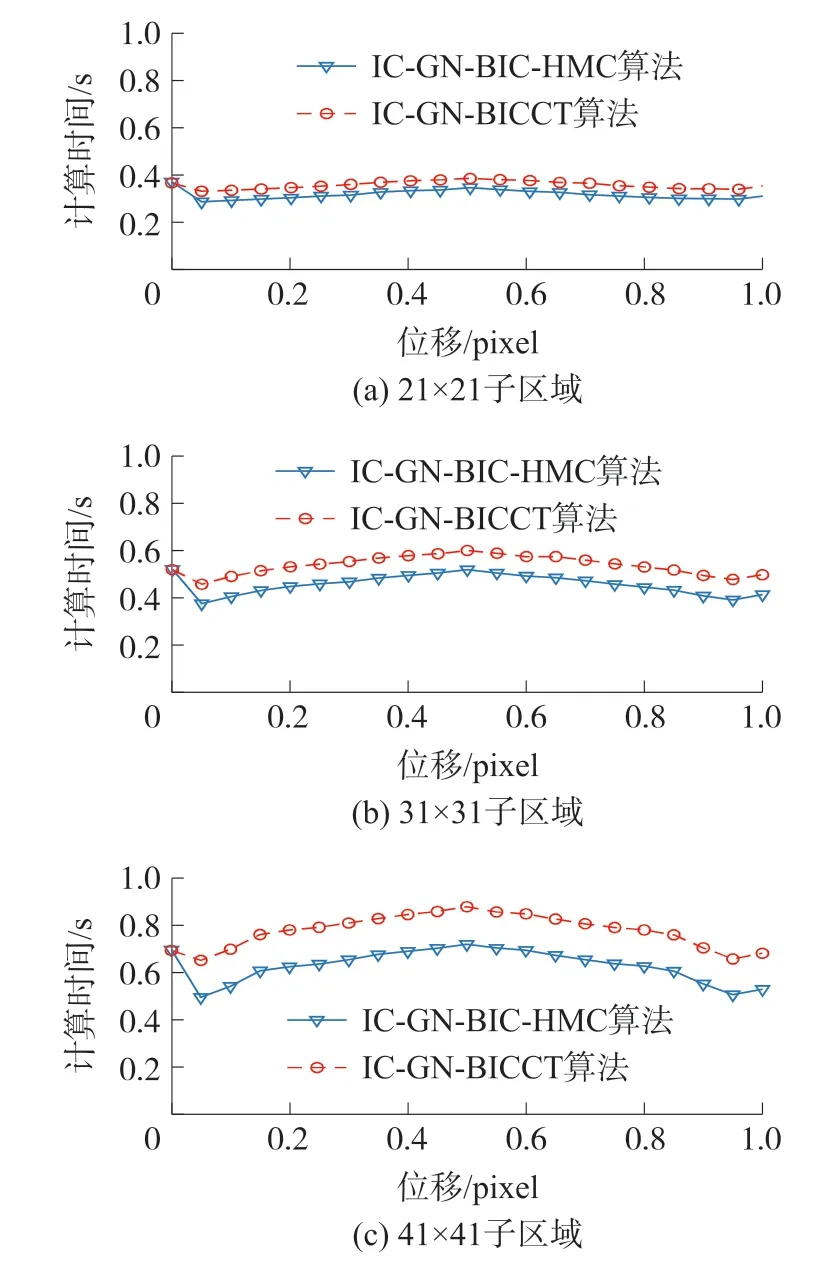
图6 使用3种不同尺寸子区域的IC-GN_BIC_HMCT和IC-GN_BICCT的计算时间比较

对于31×31和41×41的子区域，IC-GN_BIC_HMCT的效率分别提高了14.95%和18.93%。可以得出结论，子区域的尺寸越大，本算法的效率提高越多。

为了更进一步解释为什么IC-GN_BIC_HMCT算法比IC-GN_BICCT耗时少，我们在表1中列出了IC-GN_BICCT每一步的执行时间。表1中记录了图4所示的RoI左上方起的种子点1的计算时间。在表1中，第1行的海森矩阵及逆的计算步骤占算法总耗时的20.60%。如果这个计算时间减少，那么计算效率就会提高。

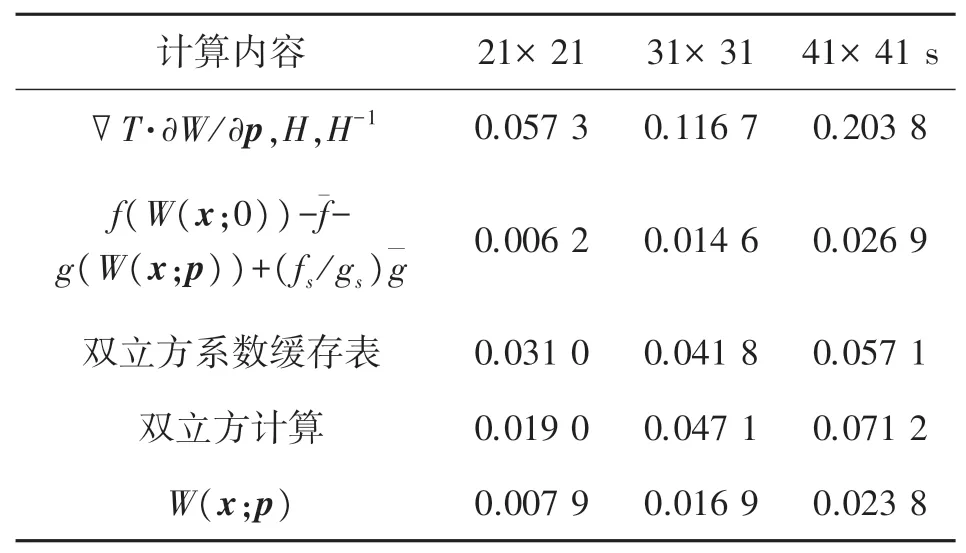
表1 用3种不同尺寸子区域的IC-GN_BICCT主要步骤的消耗时间 单位:ms

在表1中，当子区域大小为31×31和41×41像素时，计算海森矩阵及逆的时间成本分别为IC-GN_BICCT总时间成本的22.80%和29.79%。这也说明了为什么子区域尺寸越大，效率提高越多。

2.2 使用CCD摄像机采集的真实图像进行位移和变形测量

为了实际验证本算法对真实散斑图像的有效性和效率，我们使用万能材料试验机进行了试样拉伸实验，计算试样的位移和变形量。通过喷涂油漆，被测试样上覆盖了黑白散斑图案。CCD摄像机被用来采集拉伸前后的一组图像，图7为试样未变形时的参考图像。试样受力方向为图中Y轴正方向。图像的分辨率为1 624×1 234像素，灰度阶数为8位。摄像机采样频率为2帧/s。在试样断裂之前，总拉伸时长约为45 s。RoI尺寸设置为121像素×365像素。在X、Y坐标方向上，每两个种子点的间隔为10个像素。因此需要计算的种子点数量为13×37＝481个。为了提高计算效率，计算变形图时使用21×21像素尺寸子区域。

图7 被测试样与RoI

获得RoI中所有种子点的位移后，还要使用双立方插值方法重建全场变形图，每两个配准的种子点之间需要插入额外的9个点。图8显示了第10帧变形图像的X轴和Y轴上RoI的位移和变形分布图。图中的标尺上的数字表示位移和变形量的大小。图中可见试样在Y轴方向上伸长，而在X轴方向上收缩。

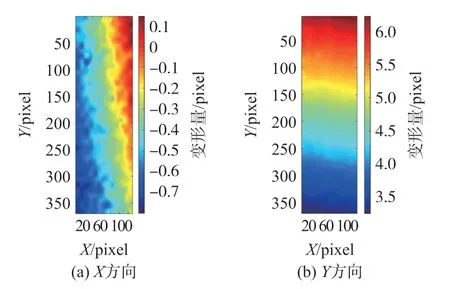
图8 第10幅变形图像的X、Y方向上试样的全场变形图

下面分析本算法对连续变形场计算效率的提高。表2给出了分别使用IC-GN_BIC_HMCT和IC-GN_BICCT[20]、IC-GN算法[18－19]计算连续20帧图像配准的平均时间。可以看出由于使用了插值系数缓存方法，使用21×21像素尺寸子区域时，计算时间从IC-GN算法的0.42 s/帧减少到0.21 s/帧，而使用41×41像素尺寸子区域时，计算时间更是从IC-GN算法的1.23 s/帧减少到0.55 s/帧，效率提高了123.63%。

表2 使用3种不同尺寸子区域的IC-GN算法、IC-GN_BIC_HMCT算法、IC-GN_BICCT消耗时间单位:s/frame

为了进一步比较IC-GN_BIC_HMCT和IC-GN_BICCT两种算法的计算时间，在图9给出了每帧图像的计算效率对比曲线。图9中使用的是21×21尺寸子区域。当第1帧变形图像与参考图像配准时，由于参考图像的H矩阵没有被缓存，IC-GN_BIC_HMCT和IC-GN_BICCT[20]两种算法计算时间基本相等。从第2帧变形图像开始，IC-GN_BIC_HMCT的计算时间明显低于IC-GN_BICCT。IC-GN_BIC_HMCT算法计算20帧图像配准所用时间为4.27 s，而IC-GN_BICCT算法为5.22 s。前者比后者快18.20%。该结果显示了新算法在效率方面的优越性。除去第1幅变形图像，后续的19幅图像的计算效率提高了19.02%。

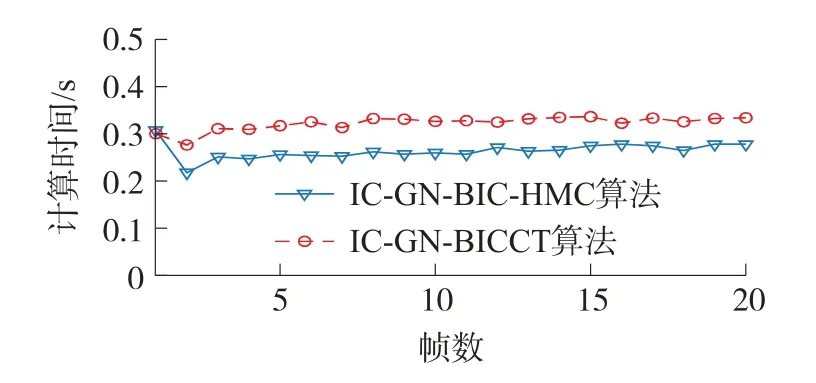
图9 使用真实散斑图像的计算效率比对

3 结论

本文采用了一种新的连续散斑图像配准方法，称为IC-GN_BIC_HMCT算法。考虑到IC-GN中需要计算海森矩阵及逆，本研究致力于减少连续数字图像相关中的IC-GN计算时间。在已有变形图像的双立方插值系数缓存表的基础上，又建立了参考图像海森矩阵缓存表。利用缓存表避免了海森矩阵及逆的重复计算。通过实验验证了该算法的正确性和有效性。在人工模拟散斑图像实验中，对于3种不同大小的子区域，本算法的效率分别比没有海森矩阵缓存表的IC-GN-BICCT算法高11.35%、14.95%和18.93%，但精度相同。在真实散斑图像实验中，计算效率提高了18.20%。测试结果表明了该算法在效率上的优越性。