基于全阶自适应的PMSM无速度传感器抗扰控制

贾超广，肖海霞

(1.郑州升达经贸管理学院信息工程学院，河南 郑州 451191；2.河南工程学院，河南 郑州 451191)

在高性能永磁同步电机控制系统中，准确地获取电机转子位置和转速信息是系统稳定运行的关键因素。转子位置和转速信息一般是通过机械式传感器测量得到的，但机械式传感器由于存在成本较高、安装相对复杂、维护困难、增大系统体积、降低系统可靠性等缺点，极大地限制了其应用场合[1－2]。为了解决上述问题，通常采用无速度传感器控制技术来获得电机转子位置和转速，该技术具有适应性强、适用范围广、节约成本、易于维护等优点。

目前，常见的无速度传感器控制有卡尔曼滤波器法、模型参考自适应[3]、人工智能算法、全阶自适应观测器[4－7]等。卡尔曼滤波器法对硬件有较高的要求，不易实现；模型参考自适应法对系统参数依赖过大，鲁棒性较差；人工智能算法虽然不依赖于电机模型参数，但是其算法复杂，硬件实现有一定难度；全阶自适应观测器具有结构简单、易于实现、便于计算、通用性强等优点而受到广泛关注。但该方法对外部负载变化较为敏感，当负载发生突变时，存在转速跌落过大，恢复时间过长的问题，进而影响控制系统的性能。针对这一问题，本文提出了一种基于全阶自适应的永磁同步电机无速度传感器抗扰控制方法，有效地抑制了负载突变对控制系统性能的影响。

1 全阶自适应观测器设计

永磁同步电机(permanent-magnet synchronous motor，PMSM)在旋转坐标轴下数学模型为:

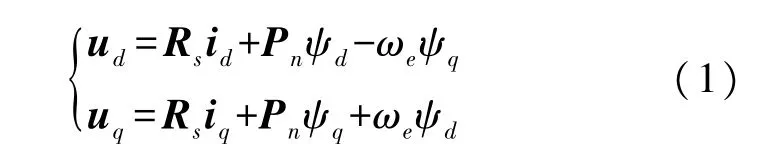
式中:id和iq、ud和uq、ψd和ψq分别为定子电流、定子电压和永磁体磁链ψf在d、q轴上的分量，Rs为定子电阻，ωe为电角速度。

由式(1)可得PMSM 在旋转坐标轴下的状态方程为:

根据式(2)建立全阶状态观测器，于是有:

在实际中，原系统与重构系统的初始状态可能不完全相同，且存在其他干扰，式(4)所示的开环观测器不能直接使用。因此引入电流误差构成反馈校正项，用以校正式(4)可得:

反馈校正项是将被观测系统的输出值与重构系统的输出值之差作为校正变量，经过增益矩阵G反馈到重构系统中构成闭环系统。由此可以确定全阶状态观测器为:

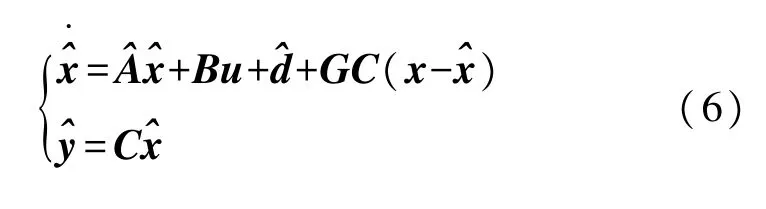
为了获得估计转速，将永磁同步电机作为参考模型，将式(6)所示的全阶状态观测器作为可调模型，用两个模型的输出误差来驱动自适应机构，在自适应规律的作用下，能不断地修正参数，以使两个模型的输出误差趋向于零。

根据Popov 超稳定性理论可以证明该控制系统是渐进稳定的。由稳定性分析可以得到转速自适应率为:

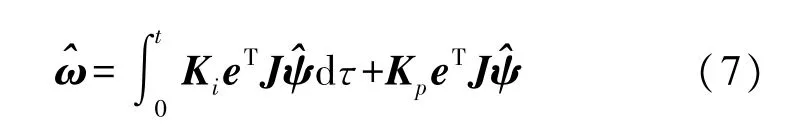
本文采用PI 控制方式来获得转速，其表达式为:

2 负载扰动观测器设计

2.1 扰动观测器设计过程

PMSM 动态空间状态方程为[8]:

式中:x为状态量，u为输入，f为扰动，y为输出，A、Bu、Bf和C为系数矩阵，则扰动项可以表示为:

如果扰动的变化率近似为零，那么f的估计就符合扰动观测器的设计原理，当扰动估计与实际扰动f非常接近时，可构造扰动观测器为:

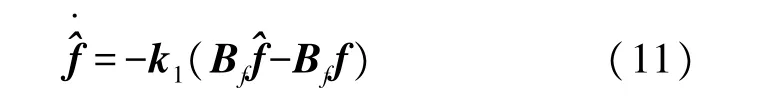
式中:k1为增益系数。

对式(10)、式(11)进行整理可得扰动估计表达式为:

设中间变量矩阵N，令则式(12)可以写为:

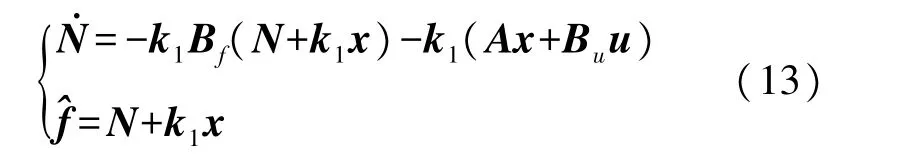
此时式(13)即为扰动观测器方程，结合永磁同步电机的扩展运动方程我们可以得到PMSM 的负载扰动观测器方程为:

根据Lyapunov 稳定性要求可以证明增益系数k1的取值范围是k1<0。

2.2 转矩电流前馈补偿

负载突变会引起转矩电流的变化，因此可以根据突变的负载扰动对转矩电流进行补偿。扰动补偿值可以表示为:

式中:Pn为电机极对数，此时，转矩电流给定值可表示为:

3 自抗扰控制器设计

自抗扰控制器[9](ADRC)由跟踪微分器(TD)、扩张状态观测器(ESO)和状态误差反馈控制律(NLSEF)三部分构成。其中跟踪微分器实现转速信号的提取，跟踪给定转速的同时避免了经典PI 控制器中微分环节的噪声放大作用；扩张状态观测器将输出中的扰动量扩展为新的状态变量通过反馈进行补偿；误差反馈控制律是将TD 计算的误差与ESO 的反馈量进行非线性组合，最终实现补偿。

跟踪微分器(TD)以给定值v0作为输入，微分信号v1、v2作为输出，则其设计如下:

式中:h为步长，fhan为快速最优控制函数，具体函数如下:

以系统输出量y和系统的实际输入量u来跟踪系统的状态变量及扰动的ESO 可以设计为:

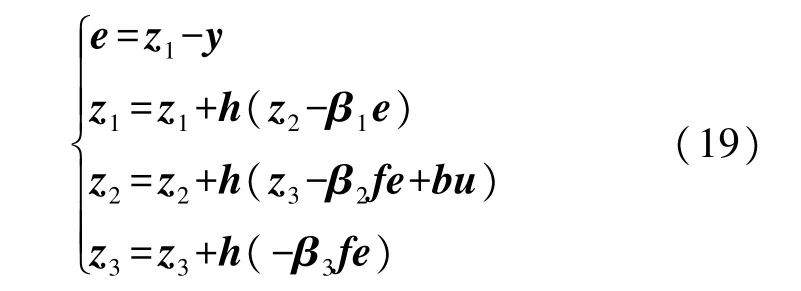
式中:β1、β2、β3为误差系数，b为可调系数。

则ADRC 的状态误差反馈控制律可以表示为:

式中:p为e1、e2的系数，k为可调参数。

则该ADRC 的补偿过程可以表示为:

基于全阶自适应的永磁同步电机无速度传感器抗扰控制框图如图1 所示。

图1 基于全阶自适应的永磁同步电机无速度传感器抗扰控制

4 实验结果及分析

本文的实验是在基于TMS320F28335 数字信号处理器(DSP)的实验平台上完成的。实验中所用电机参数为:额定电压:200 V，额定电流:10 A，额定转矩:6.37 N▪m，额定转速:3 000 r/min，极对数:5 对，转动惯量:0.000 368 kg▪m2，定子电阻:0.18 Ω。实验平台由三部分组成，包括两电平电压源型逆变器、永磁同步电机及磁滞测功机，如图2 所示。

图2 实验平台

为了验证所提出控制策略对抑制外部负载突变的有效性，分别对传统的全阶自适应观测器无速度传感器控制、加入负载扰动观测器的全阶自适应观测器无速度传感器控制、采用ADRC＋负载扰动观测器的全阶自适应观测器无速度传感器控制进行了抗负载突变的的实验研究，同时对比了三种控制策略在空载稳态运行及负载突变时的实验波形，实验结果如图3～图7 所示。

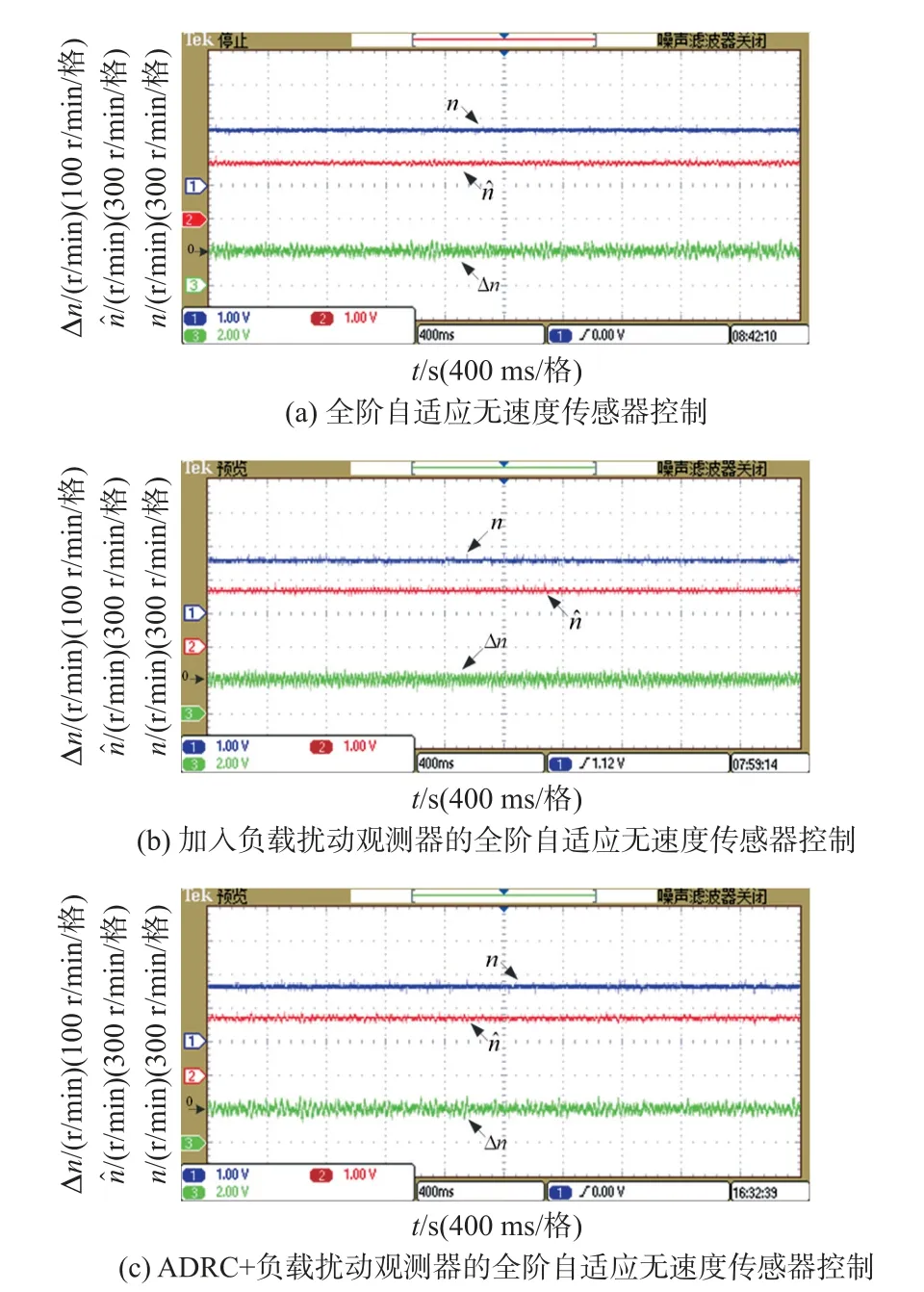
图3 三种控制策略空载稳定运行于500 r/min 时转速及转速误差实验波形

图3 为三种控制策略在给定转速500 r/min 时电机空载稳态的实际转速n、估计转速和转速误差Δn实验波形。从图3 中可以看出三种控制策略在500 r/min 时估计转速能够跟随实际转速且转速误差约为20 r/min。

图4 为三种控制策略在给定转速2 000 r/min时电机空载稳态的实际转速n、估计转速和转速误差Δn实验波形。由图4 我们可以看出三种控制策略估计转速也能跟随实际转速且转速误差约为25 r/min。

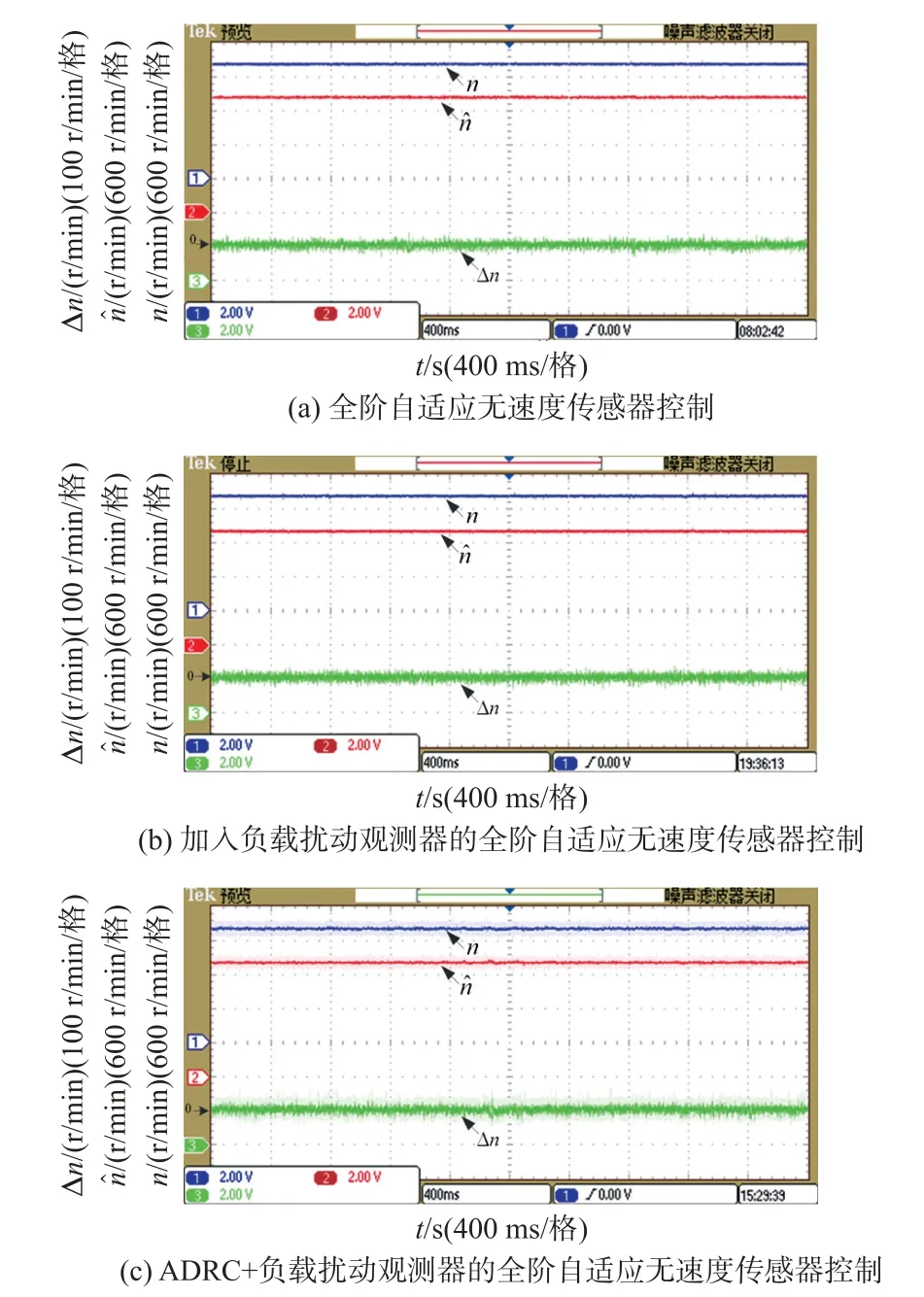
图4 三种控制策略空载稳定运行于2 000 r/min 时转速及转速误差实验波形

从图3 和图4 可以看出，不论系统处于低速还是高速，三种控制策略下的估计转速均能跟随实际转速且转速误差较小，稳态性能良好，表明了所提出方法的可行性。

图5 为三种控制策略下电机空载运行于1 000 r/min 时突加50%额定负载的实际转速n、估计转速和q轴电流实验波形。从图5 可以看出传统的全阶自适应无速度传感器控制在突加50%额定负载时转速跌落大约为120 r/min，转速恢复时间约为1 s；加入负载扰动观测器的全阶自适应无速度传感器控制转速跌落大约为100 r/min，恢复时间约为0.6 s；采用ADRC＋负载扰动观测器控制的全阶自适应无速度传感器控制转速跌落大约为60 r/min，恢复时间约为0.6 s。

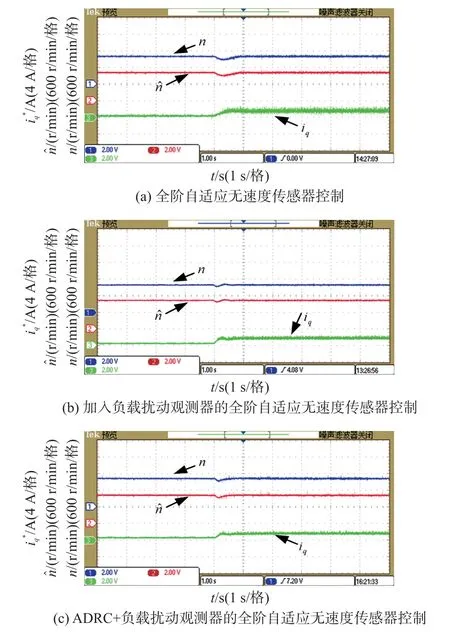
图5 三种控制策略在1 000 r/min突加50%额定负载实验波形

图6 为三种控制策略下电机空载运行于1 000 r/min 时突加额定负载的实际转速n、估计转速和q轴电流实验波形。从图6 可以看出传统的全阶自适应无速度传感器控制在突加额定负载时转速跌落大约为180 r/min，转速恢复时间约为1 s；加入负载扰动观测器的全阶自适应无速度传感器控制转速跌落大约为120 r/min，恢复时间约为0.6 s；采用ADRC＋负载扰动观测器控制的全阶自适应无速度传感器控制转速跌落大约为80 r/min，恢复时间约为0.6 s。

图6 三种控制策略在1 000 r/min突加额定负载实验波形

图5 和图6 说明在同一种工况下，针对不同程度的负载突变，三种控制策转速在轻微波动之后均能快速回到给定，采用负载扰动观测器的全阶自适应无速度传感器控制相比于传统方法转速跌落减小，恢复时间加快；而采用ADRC＋负载扰动观测器控制的全阶自适应无速度传感器控制具有更小的转速跌落以及更快的恢复时间。表明本文所提出的控制策略具有良好的抗负载突变能力，能够有效抑制负载突变对电机转速的影响。

图7 为三种控制策略下电机空载运行于2 000 r/min 时突加50%额定负载的实际转速n、估计转速和q轴电流实验波形。

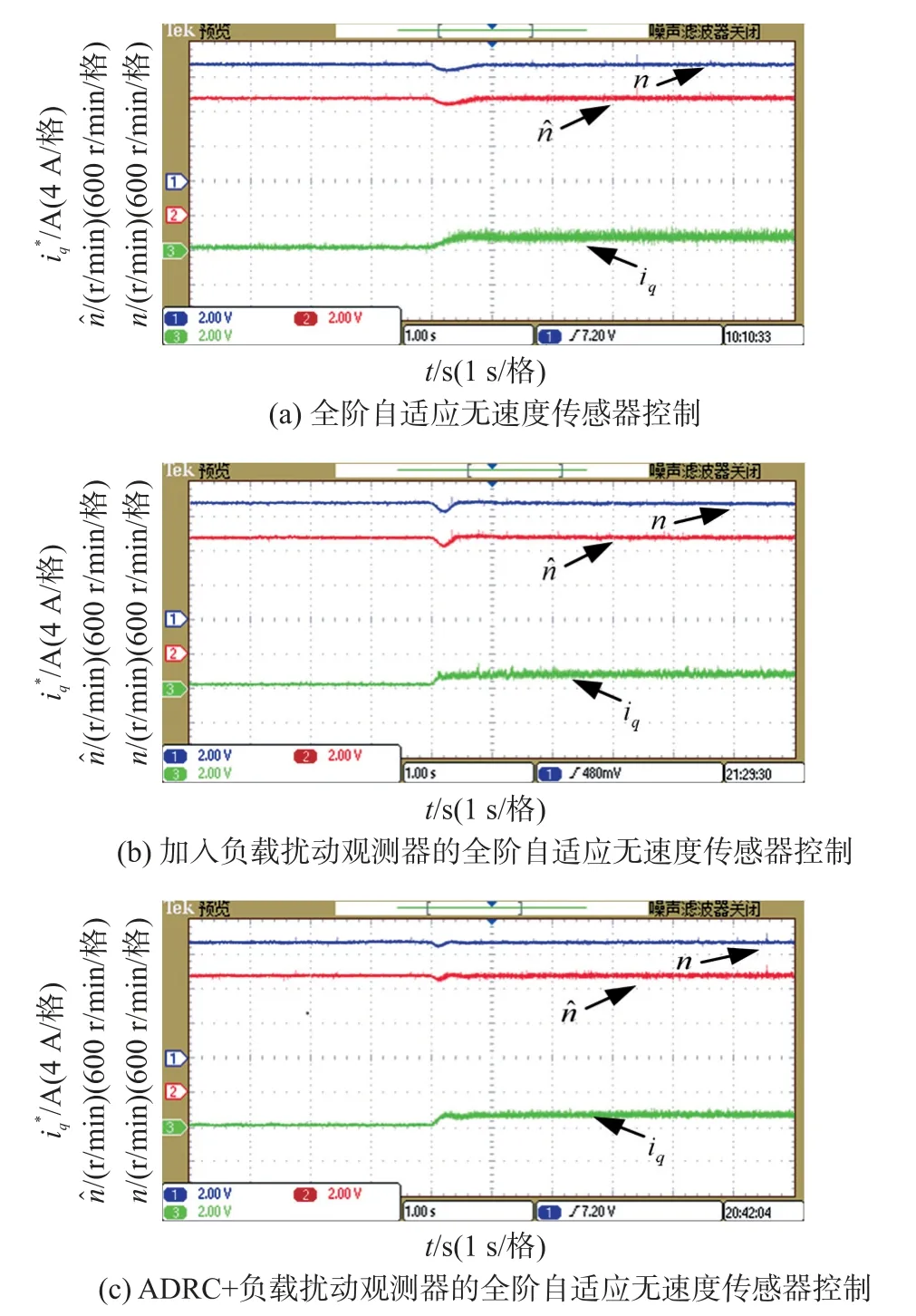
图7 三种控制策略在2000r/min 突加额定负载实验波形

从图7 可以看出传统的全阶自适应无速度传感器控制在突加50%额定负载时转速跌落大约为120 r/min，转速恢复时间约为0.8 s；加入负载扰动观测器的全阶自适应无速度传感器控制转速跌落大约为140 r/min，恢复时间约为0.4 s；采用ADRC＋负载扰动观测器控制的全阶自适应无速度传感器控制转速跌落大约为80 r/min，恢复时间约为0.4 s。

从图5～图7 可以看出，无论是低速还是高速，半载还是满载，三种控制策略均能够在转速跌落之后能够迅速回归给定，其中传统全阶自适应无速度传感器控制转速跌落最大，恢复时间最慢；加入负载扰动观测器的全阶自适应无速度传感器控制转速跌落明显减小，恢复时间加快；而采用ADRC＋负载扰动观测器的方法转速跌落最小，恢复时间最快。

5 结论

本文针对负载突变的变化对永磁同步电机全阶自适应观测器无速度传感器控制系统转速性能的影响，提出了一种负载突变抑制的方法来提高控制系统的抗扰性。该方法以全阶自适应观测器的设计原理为基础，利用电机的机械运动方程来构造负载扰动观测器并对控制系统进行电流前馈补偿，同时采用ADRC＋负载扰动观测器的方法进一步提升控制系统抗扰性能。实验结果表明本文所提出的方法在保持全阶自适应观测器无速度传感器控制系统良好稳态性能的同时，可以有效地减小负载突变对电机转速性能的影响，提高了系统的抗负载扰动能力。