基于改进灰色GM(1.1)模型的铁路货运量预测
2021-07-16肖金山
肖金山,何 涛
(兰州交通大学 研究院,兰州 730070)
铁路货运量预测是铁路货运部门进行运输规划和科学决策的重要依据,科学准确的预测结果将为铁路货运规划方案的实施提供有力保障.国外对铁路货运量的预测研究相对较早,文献[1]通过多元回归模型对铁路货运量进行预测;文献[2]采用神经网络对港口多式联运货运量预测研究;文献[3]更是率先使用Box-Jenkins模型对短期货运量进行了预测.国内铁路货运量的预测研究主要集中于年度长期预测.文献[4]通过遗传算法和神经网络的混合运算对铁路年度货运量进行预测;文献[5]利用无偏灰色Verhulst对兰州至中川机场年度货运量预测研究;文献[6]则通过灰色关联分析选取年度货运量的主要影响因素,并建立支持向量机模型完成铁路年度货运量的最终预测.由于铁路货运部门制定月度货运计划时,年度货运量预测在货运规划方面的指导意义较小,若能科学准确的对铁路月度货运量进行预测,将有效解决我国铁路短期货运量规划参考理论不足的问题.
铁路月度货运量的影响因素较多,准确的对各因素定量分析存在较大难度,使得普遍应用于铁路年度货运量预测的基于线性回归、指数分析的传统建模方法,因没有长期有效的月度观测资料无法有效使用.灰色GM(1.1)模型以贫信息、小样本为研究对象,提供了不确定性系统解决问题的新思路[7].若将铁路月度货运量看作一个灰色系统,对监测得到的较少信息进行累加变换,使原始货运量呈现指数增长现象后,建立GM(1.1)模型对铁路月度货运量进行预测将存在理论依据.文献[8-12]采用传统GM(1.1)模型对铁路年度货运量进行预测研究,由于选取的铁路货运量样本呈非负单调增长趋势,预测精度较高.文献[13-14]则对呈现振荡波动现象的铁路年度货(客)运量序列直接采用传统GM(1.1)建模,因没考虑样本序列波动的情况,预测精度较差.由此表明,传统GM(1.1)模型仅对样本呈现非负单调变化的序列适用性较强,对于存在波动现象的序列预测效果并不理想.
查阅国家统计局相关资料发现,铁路月度货运量序列时常呈现非负波动现象,为解决铁路月度货运量存在振荡波动现象时,传统GM(1.1)建模方法预测效果不理想的问题,本文使用加速平移与加权均值变换对存在波动现象的铁路月度货运量序列预先处理,使其满足非负单调条件后进行改进GM(1.1)建模.
1 灰色GM(1.1)模型
1.1 传统GM(1.1)
传统GM(1.1)模型基本思想是:为方便数学建模,对原序列进行一次累加生成,因累加后序列具有指数增长趋势,所以利用近似一阶微分方程建立模型,最后由建模序列累减生成预测序列完成原序列发展趋势的预测[15-16].
传统GM(1.1)具体建模过程如下:
设原序列为:X(0)={x(0)(1),x(0)(2),…,x(0)(n)},对该序列进行一次累加生成:
(1)
生成具有指数规律的序列为
X(1)={x(1)(1),x(1)(2),…,x(1)(n)}.
将X(1)序列近似为一阶微分方程
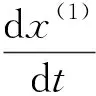
(2)
的解.其中:a为模型的发展系数;b为灰作用量.
记参数A=[a,b]T,利用最小二乘法求得A为
A=(BTB)-1BTY.
(3)
式中:
Y={x(0)(2),x(0)(3),…,x(0)(n)}T.
求得a,b值并代入公式(2),计算得
(4)
由公式(4)累减可得预测函数为
(5)
1.2 振荡序列的传统GM(1.1)误差分析
传统GM(1.1)建模时,因原序列规律性不强,需进行累加变化后利用公式(2)建立数学模型.此建模方式不论原序列振荡与否,累加生成的序列都将非负单调变化,还原序列也呈相同变化趋势.当原序列非负单调时,预测精度较好,但当原序列振荡波动时,因还原序列非负单调变化,无法准确拟合原振荡序列,预测精度并不理想.
1.3 振荡序列的GM(1.1)模型改进
若对振荡波动序列进行数学变换使其具有非负单调趋势后,利用GM(1.1)建立数学模型,最后计算还原函数并进行数学反变换得到预测序列,将很好的解决传统GM(1.1)模型对振荡序列预测精度不高的问题.对于振荡序列的数学变换,学者们提出了不同的思想,主要包括利用指数变换、三角变换、正弦函数变换、平移变换、加权均值、几何平均和缓冲算子等方法处理振荡序列[17-21].本文参照文献[18,21],结合加速平移与均值变换方法对呈现振荡波动现象的序列预先处理,达到弱化序列波动性的目的.
设X={x(1),x(2),…,x(n)}为原序列,若存在k,k′∈[1,2,…,n-1],使x(k+1)-x(k)>0,x(k′+1)-x(k′)<0,则称X为随机振荡序列.令:
M=max{x(k)|k=1,2,…,n},
(6)
m=min{x(k)|k=1,2,…,n},
(7)
称M-m为序列X的振幅,记为T.
定义加速平移变换:为了对原振荡序列的波动性进行弱化,特定义序列XE1={x(1)e1,x(2)e1,…,x(n)e1},式中:
x(k)e1=x(k)+(k-1)T,k=1,2,…,n.
(8)
称e1为加速平移变换因子,通过简单数学运算即可证明经过该变换后的原始非负振荡序列呈单调变化趋势.
定义加权均值变换:经过e1因子处理后的序列已呈现单调变化趋势,具备建模条件.为了更加准确的对原序列进行拟合,引入加权均值变换对因子处理后的序列进行二次变换.定义变换序列为XE2={x(1)e1e2,x(2)e1e2,…,x(n)e1e2},式中:
(9)
称e2为加权均值变换因子,通过简单数学计算可证明经过e2因子变换后的序列保持了原有序列的单调特性且使序列更加光滑.
2 振荡序列的改进GM(1.1)建模
设原振荡序列为X(0)={x(0)(1),x(0)(2),…,x(0)(n)},其中:x(0)(k)>0,k=1,2,…,n.改进GM(1.1)建模过程如下:
1) 对原序列X(0)进行e1因子变换为
Y(0)={y(0)(1),y(0)(2),…,y(0)(n)}.
2) 对序列Y(0)进行e2因子变换为
Z(0)={z(0)(1),z(0)(2),…,z(0)(n)}.
3) 对序列Z(0)进行一次累加为
Z(1)={z(1)(1),z(1)(2),…,z(1)(n)}.
4) 建立Z(1)序列的GM(1.1)微分方程模型:
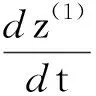
(10)
a,b参数由最小二乘法
(11)
确定,其中:
P=[z(0)(2),z(0)(3),…,z(0)(n)]T.
5) GM(1.1)微分方程的响应函数为
(12)
6) 一次累减得到z(0)的预测函数为
(13)
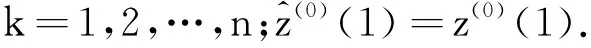
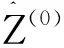
(14)
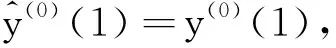
(15)
(16)
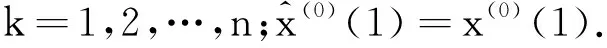
9) 精度检验.利用残差值和相对误差指标对改进GM(1.1)模型预测精度进行评价,并和传统GM(1.1)模型对比分析.
设残差值序列为
e={e(1),e(2),…,e(n)}.
其中:
(17)
则相对误差为
(18)
平均相对误差为
(19)
3 数值模拟验证
如表1所列我国2019年11月至2020年5月铁路货运量统计数据为例,分别使用传统GM(1.1)和改进GM(1.1)建立铁路月度货运量预测模型.通过比较预测货运量与实际货运量的拟合程度,对两种建模方法的模拟精度进行对比分析.
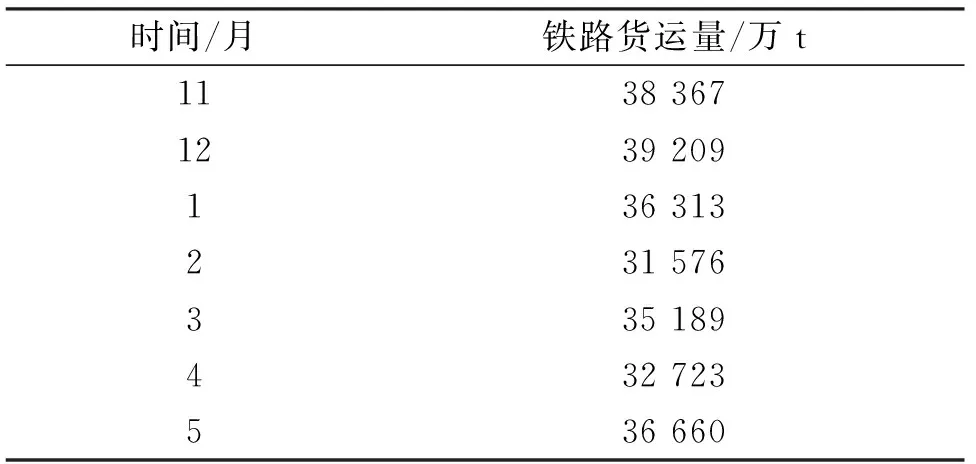
表1 2019年11月至2020年5月我国铁路月度货运量统计表Tab.1 Statistical table of China′s railway monthly freightvolume from November,2019 to May,2020
1) 利用表1数据建立传统GM(1.1)模型.原数据序列为X(0)={38 367,39 209,36 313,31 576,35 189,32 723,36 660}.对原序列累加一次得X(1)={38 367,77 576,113 889,145 465,180 654,213 377,250 037}.
通过公式(3)利用最小二乘法求A,其中:

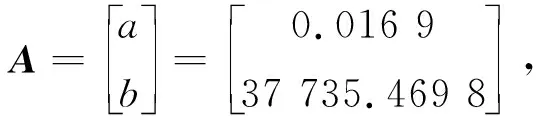
由公式(5)可得传统GM(1.1)模型预测函数为
将k=1,2,3,4,5,6代入上式,得到传统GM(1.1)对2019年11月至2020年5月我国铁路月度货运量的模拟结果为
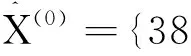
35 553.202 1,34 957.401 6,34 371.585 6,33 795.586 7}.
2) 利用表1数据建立改进GM(1.1)模型.原序列为X(0)={38 367,39 209,36 313,31 576,35 189,32 723,36 660}.由原数据得X(0)序列的振幅T=7 633.
根据公式(8)对X(0)进行e1因子变换得:Y(0)={38 367,46 842,51 579,54 475,65 721,70 888,82 458}.
根据公式(9)对Y(0)进行e2因子变换得:Z(0)={38 367,42 604.5,45 596,47 815.75,51 396.8,
54 645.333 3,58 618.571 4}.
原序列经过e1和e2因子处理后呈非负单调变化趋势,以Z(0)数据建立GM(1.1)模型.Z(0)的一次累加生成序列为
Z(1)={38 367,80 971.5,126 567.5,174 383.25,225 780.05,280 425.383 3,339 043.954 7}.
公式(11)中,参数B,P分别为

P=[42 604.5,45 596,47 815.75,51 396.8,
54 645.333 3,58 618.571 4]T.
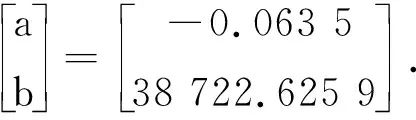
由公式(12)可得一阶微分方程的解为
由公式(13)可得改进GM(1.1)模型预测函数为:
将k=1,2,3,4,5,6代入上式,得到改进GM(1.1)对Z(0)的预测结果为
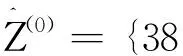
51 411.348 2,54 781.849 7,58 373.319 6}.
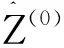

33 531.862 2,33 469.357 2,34 124.139}.
为了准确分析两种模型的预测精度,对传统GM(1.1)模型和通过e1和e2因子变换后生成新的序列建立的改进GM(1.1)模型的预测结果与实际货运量进行比较分析,结果如表2所列,如图1所示.
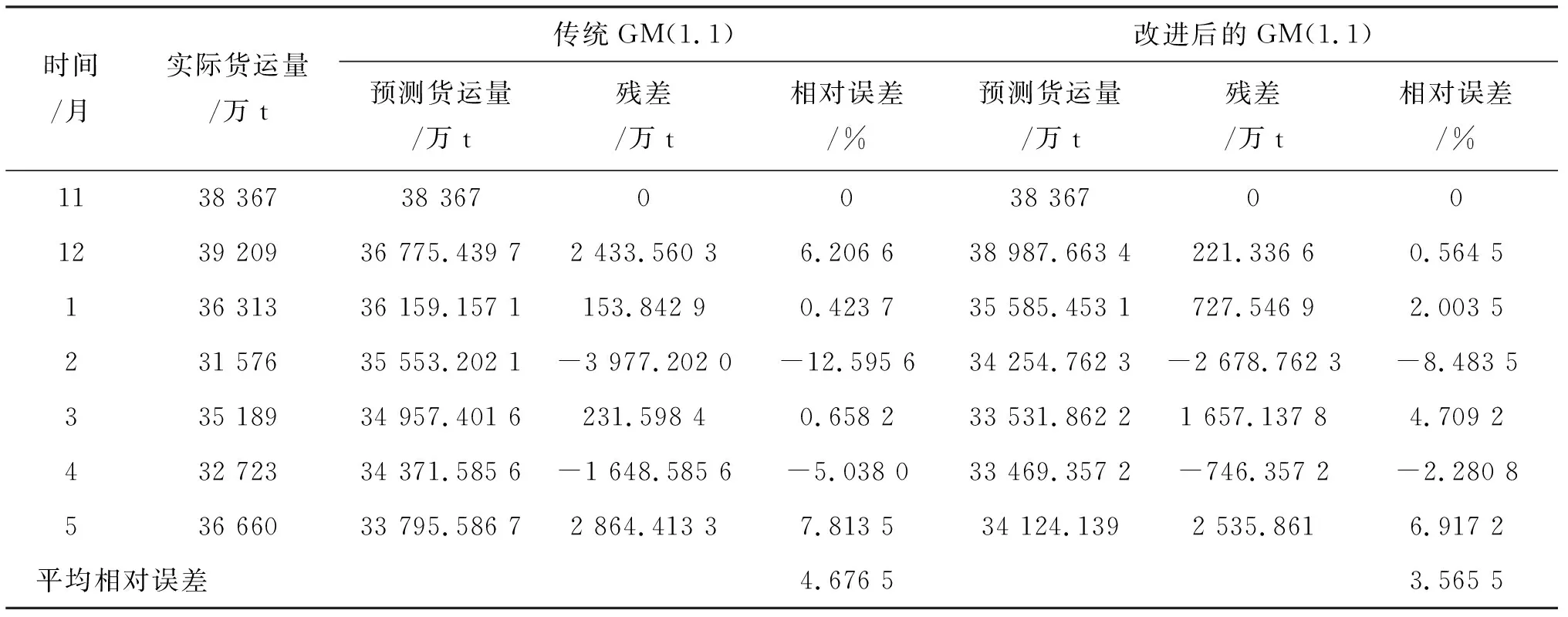
表2 两种模型预测数据及误差分析Tab.2 Prediction data and error analysis table of the two models
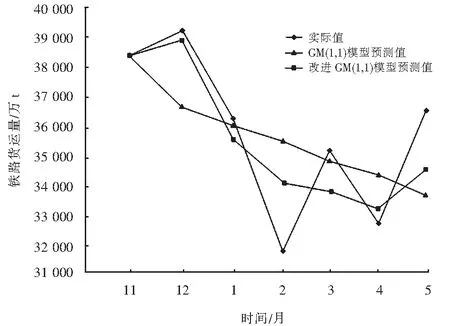
图1 两种模型拟合曲线Fig.1 Fitting curves of the two models
结果表明,和传统GM(1.1)相比,对呈现振荡现象的铁路月度货运量使用e1和e2因子变换后建立的GM(1.1)模型在残差、相对误差和平均相对误差三项指标均有减小,且预测结果呈现波动变化趋势,更好的拟合了铁路月度货运量原始序列,解决了传统GM(1.1)模型对振荡波动序列模拟度差的问题.
4 结论
针对传统GM(1.1)对呈现振荡波动现象的铁路货运量预测效果不理想的问题,本文建立改进GM(1.1)模型.通过模拟我国铁路月度货运量,对两种模型的拟合效果进行了比较分析,主要结论如下:
1) 传统GM(1.1)建模时,由于还原后的预测函数呈非负单调变化,导致预测序列也呈相同变化趋势,这是造成传统GM(1.1)模型对振荡序列预测效果差的主要原因.通过拟合我国2019年11月至2020年5月铁路货运量发现,经过e1和e2因子变换后的改进GM(1.1)模型在残值、相对误差和平均相对误差指标和传统GM(1.1)模型相比下降明显,验证了改进GM(1.1)模型对呈现振荡波动现象的铁路月度货运量预测的可行性.
2) 对铁路月度货运量的拟合和预测,按年份顺序进行月度数据横向分析大幅提高了预测精度.由于影响铁路月度货运量的因素众多且复杂,后续研究将考虑外在因素对预测结果的影响,并加入不同年份同一月份的纵向月度货运量预测值,结合两种预测结果通过最优组合法得到预测实际值,以进一步提高铁路月度货运量的预测精度.
