素数无穷性质证明的分层教学设计*
2021-07-16张艳硕李泽昊戴君熹
张艳硕 李泽昊 戴君熹
北京电子科技学院,北京市 100070
1 引言
素数,指在大于1 的自然数中,仅以1 和自身作为其因子的自然数[1]。 素数的无穷性质指在自然数中,素数有无穷多个的性质。 证明素数的无穷性质有多种方法,其难度不同,有些证明方法还能证明一些其他有关素数的性质。 素数在数学、计算机科学、密码学特别是信息安全等多个领域中均具有重要地位[2],且其应用十分广泛。
现阶段,大多数学生对素数的概念有较强的理解,但是对于素数的无穷性质及其证明理解不足。 由于素数及其无穷性质在数学、密码学等领域运用广泛,其教学的重要性较高,但对不同阶段学生使用的素数无穷性质证明的教学方法大多过于单调,缺乏创新和挑战性,对于数学知识和能力较强的学生,无法起到较好的教学效果。
本文旨在提出一种素数无穷性质的分层次教学设计,由浅入深,针对不同阶段和水平的学生进行分层次的概念、应用和实践教学,让不同层次的学生更好地理解和学习素数无穷性质及其应用。 通过素数无穷性质证明教学,可以使学生对素数有更强的理解。 同时让学生联系生活实际,对素数无穷性质及其应用产生兴趣,进而对相关领域进行深入的研究,对学生数学素养的培养及其后期学习起到重要作用。
2 素数无穷性质证明的一般性教学
现阶段,密码的应用越来越广泛,素数的性质研究有了进一步的提高,很多理工科专业都会在许多相关课程教学实践中进行素数无穷性质的教学设计和应用实践。 但当前的素数无穷性质的教学较为单调,缺乏相应的应用环节和实践环节,不能很好地满足不同阶段和不同层次学生的教学需求和知识需求。
2.1 素数无穷性质及其证明
素数是一个非常重要的数学概念,其具备很多性质。 素数有无穷个,素数无穷性质现行证明教学一般使用Euclid[3]证明法,这是最经典的证明方法,证明的难度一般,基本适合数论等相关课程的教学和学生学习。
2.2 证明方法的一般教学方法
素数无穷性质的Euclid 证明法较为简单易懂,适合对数学基础较低的学生进行教学,一般教学方法也较为简单,即讲述大致证明过程,学生理解即可达到教学目的。 以下为其证明过程:
使用反证法,设素数为有限集{p1,…,pr},考察数n=p1p2···pr+1。n不属于集合{p1,…,pr},因此是合数,所以n有一个素因子p,但p一定不是某个pi,否则p将是n的因子和乘积p1p2···pr的因子,从而也是n-p1p2···pr=1 的因子,这不可能。 所以素数有无穷多个。 以上即为基于Euclid 证明法的素数无穷性质的一般教学方法。
在讲完素数无穷性质的证明之后,还可以给出素数的其他性质,如孪生素数、素数个数的计算和级数中的素数等。 这些都能帮助学生对素数性质的理解更加透彻和深刻。
2.3 存在问题
虽然上述Euclid 的一般证明方法简单易懂,教学时相对轻松,但也有其不足之处,主要体现在以下三个方面:
(1)内容单调。 证明过程较为直接,但缺乏内容。 对于水平较高的学生,可以运用难度较高,内容丰富,运用知识面更广的证明方法,扩充不同的证明方法可以增强其数学证明能力,提高其对素数及其无穷性质的认识,可以更好地掌握素数无穷性质的证明。
(2)理论深度不够。 证明的理论深度不够,证明用到的数学理论知识较少,深度不够,对于数学知识掌握较好、能力水平较高的学生,没有用到他们熟知的较为高级的知识,不能起到较好的教学效果。
(3)缺乏应用。 正如《数据安全教学方法的研究与探讨》[4]一文中指出:在对信息安全等专业学生进行数学基础教学时,证明过程缺乏应用环节,没有将素数及其无穷性质的应用进行扩展讲解,应用拓展较弱。 缺乏应用使得学习停留在理解层面,无法联系实际,不能起到最好的教学效果。 素数的无穷性质在信息安全以及密码学领域运用非常广泛,目前对于该专业和领域的学生进行教学较多,但教学实践性不强,且实践手段不够丰富。
素数无穷性证明是课程教学的重要环节,对于此性质的证明,可以设计更多的案例和方法,提高教学效果。 在教学过程中给学生展示更为生动形象的素数性质,也可以促进专业发展和素质提高,对专业课程的学习起到促进和帮助的作用。
3 素数无穷性质证明的分层次教学设计
素数无穷性质的证明有多种方式,其难度不同。 建议结合大学数学课程进行分类教学,更加具有可操作性。 对于不同层次和专业的学生,可以使用不同的证明方式进行分层次教学,以达到素数无穷性质证明的深入教学的目的。 下面将分不同阶段和专业层次,介绍不同的素数无穷性质证明的教学方案,让不同阶段和知识水平的学生了解素数无穷性质证明的不同方法。
3.1 针对大学工科新生的教学设计
此阶段学生数学有一定基础,对一些常用的数学概念以及证明方法有一定了解,可以使用Fermat 数相关性质证明素数有无限多个。 通过讲解两个定理的证明,让学生在证明了素数的无穷性质的同时也可以了解一些Fermat 数的性质等更多数学知识,同时通过学习本证明方法,学生可以更好地掌握引用已有结论进行证明的方法。
首先引入概念Fermat 数:Fermat 数是指形如22n+1 的数,其中n可以取任意自然数[5]。显然所有Fermat 数都是奇数。
引入以下两个定理:
引理 1: 设F(n)= 22n+ 1, 则有F(0 )F(1 )F(2 )···F(n-1)=F(n)-2,n≥1.
证明:使用数学归纳法。
F(0 )=3,F(1 )=5,那么n=1 时显然成立。假设n=k时成立,则当n=k+1 时:
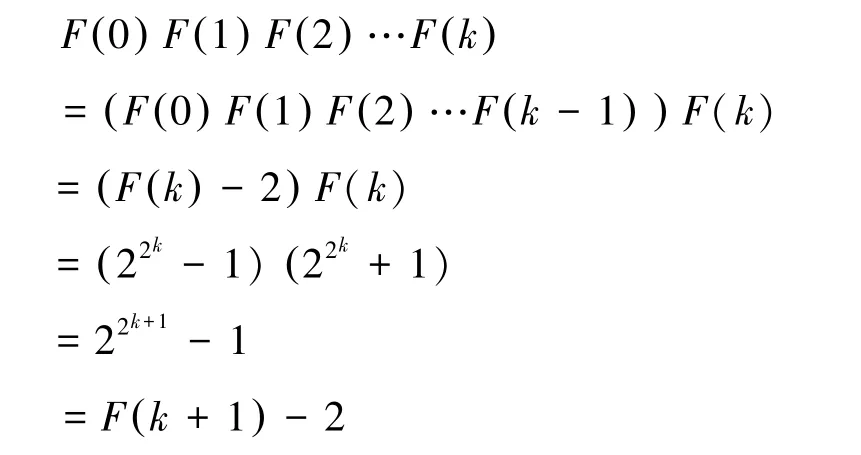
到此,即可证明引理1。
引理2:对任意两个不相等的自然数n和m,有F(n) 和F(m) 互素[6]。
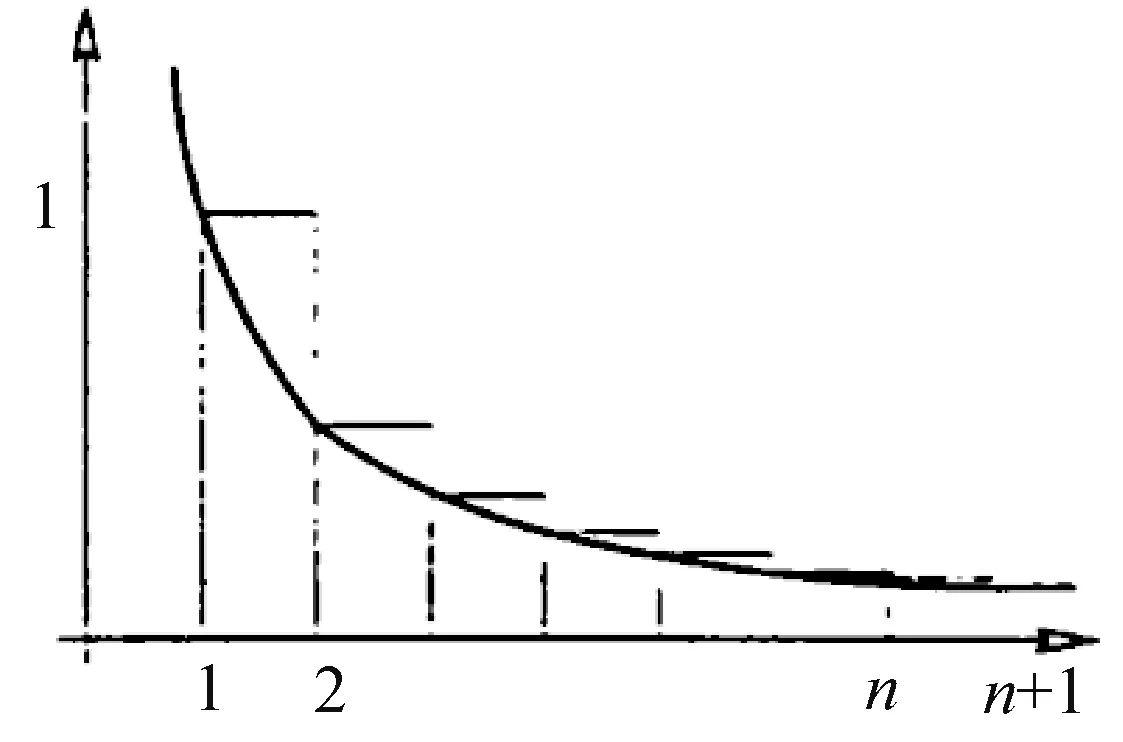
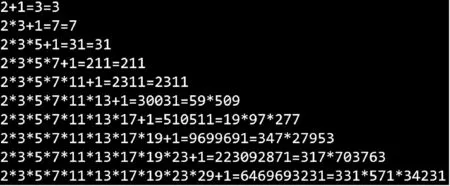
证明:假设t同时整除F(n) 和F(m),m F(n)=F(0 )F(1 )F(2 ) …F(m) …F(n-1)+2 这说明t 可以整除 F(n)-F(0 )F(1 )F(2 ) …F(m) …F(n-1)=2 注意到2 只有两个因数1 和2。 而Fermat数都是奇数,因此不可能被2 整除。 这样,t 只能为1,这就证明了任意两个Fermat 数互素。 即在自然数中有无穷多对互素的数,从而素数有无穷多个。 通过此证明方法的教学,能够较好地证明素数的无穷性质,同时,还可以使学生学习到一些关于Fermat 数和素数的性质。 教学时可以让学生对两个引理的证明过程进行验证和推广。 与Euclid 法证明相比,此方法需要有较高的逻辑推理能力,较为复杂,但在证明的教学过程中可以让学生对引用定理和所需证明内容进行联系和学习,更能提升学生的数学素养、逻辑思维和命题证明能力。 此阶段学生有一定的数学基础,能够较好地理解证明过程,逻辑思维较强,可以使用高等数学的知识,结合函数和级数的证明方法进行教学,证明过程如下[7]: 图1 函数f(t)=及其上阶梯函数 比较函数f(t)=及其上阶梯函数下方的面积,如图1 所示,则对n≤x 其中和式对其素因子都不大于x的所有m∈N进行求和。 因每个这样的m可唯一地表示成形如的乘积,故有 由于lnx无上界,所以π(x) 也无上界,从而有无限多个素数。 此证明方法结合了高等数学中的一些知识,有一定难度,但也容易理解。 与Euclid 证明法相比,使用到高等数学的内容较多,包括积分和级数的相关内容。 讲解时可以注意结合新生高等数学中已经讲过的知识,也可以作为高等数学课程的拓展学习,在实现素数无穷性证明教学的同时巩固和复习高等数学课程内容。 此阶段学生已完成大学数学基础课程的学习,有良好的数学基础和能力,可以使用较为深入的证明法进行教学。 本例使用一种利用集合的相关性质的证明方法。 首先定义一种特殊的集合:定义一种集合是一个正整数集合{a1,a2,…an}, 使得对所有不相等的i和j都有满足ai-aj整除ai,我们记这种集合为X集合。 可以证明对所有n≥2,都存在一个大小为n的满足上述条件的X集合。 证明:可以采用数学归纳法。 可以很容易地验证, {1,2} 显然是一个大小为2 的X集合。假设{a1,a2,…an} 是一个X集合。 设b0为a1*a2,*…*an(即所有ai的乘积)。 可以验证,对所有不超过n的正整数k,令bk=b0+ak,那么{b0,b1,b2,…bn} 就是一个大小为n+1 的X集合。 下面证明假设{a1,a2, …an} 是一个X集合。 则对所有不超过n的正整数i,定义fi=2ai+1,那么f1,f2,…,fn两两互素。 证明:显然fi都是奇数。 假设fk和fm(fk>fm)可以被同一个素数p整除,那么p也只能是奇数。p可以整除fk-fm即2am*(2ak-am-1)。 由于p是奇数,那么它只可能是整除2ak-am-1。 如果有s整除t,那么2s-1 整除2t-1。于是,根据X集合的定义,2ak-am-1 整除2ak-1。 那么p就可以整除2ak-1。 但p也能整除2ak+1,于是我们得出p整除2,这与p为奇数矛盾。 因此可以证明,对任意大的n, 都存在大小为n的集合,里面的数两两互素,即至少存在n个不同的素因子。 到此,素数的无穷性质得证。 使用本证明方法进行教学时,可以深入讲解利用数学归纳法进行证明的过程。 同2.2,在证明的教学过程中让学生联系和学习引用定理进行证明的方法,可以提升学生的数学素养和命题证明能力。 还可以使用一种较新发现,但是也相对简单,非常精妙的证明方法:Filip Saidak 证明法。 易知,两个相邻的自然数n和n+1 一定是互质的(否则假设此二数有大于1 的公因数k,则他们的差也应该能被k整除,但显然这不成立)。 设n> 1,由于n和n+1 是相邻自然数,因此n和n+1 是互质的。 也就是说,n的质因数和n+1 的质因数完全没有重合,因而n(n+1) 至少有两个不同的质因数。 类似地,由于n(n+1)和n(n+1)+1 是相邻自然数,因此他们是互质的,这说明n(n+1) 和n(n+1)+1 没有相同的质因数,也就是说(n(n+1))(n(n+1)+1) 至少有三个不同的质因数。 无限地递推下去,从而得出,素数必然是无穷多的。 第一种方法能够简洁地证明素数的无穷性质,但理解有一定难度,可以侧重理解进行教学,确保学生理解证明过程。 第二种方法很简单,但其思想非常新颖且精妙,值得学习,可以侧重对其证明思想进行教学。 与Euclid 证明法相比,这两种方法都可以作为很好的拓展教学。 可以引导学生将第二种证明方法和Euclid 证明法进行对比,学习其中的思想。 若学生对证明过程中引用的定理还不熟悉,可以先对所使用的引理进行简单讲解和证明,确保学生掌握证明的所有流程。 针对本阶段研究生,可以使用Mersenne 数及其相关知识进行证明的教学,使用Mersenne数和其相关性质的内容进行证明,加深证明印象,并且将其已学内容和素数的无穷性质证明进行联系,加强学生联系知识、灵活运用和融会贯通的能力。 设素数集合P有限,记其中的最大素数为p,Mersenne 数指形如2p-1 的数。 我们通过证明Mersenne 数的每个素因子q都大于p,从而证得结论。 设素数q整除2p-1,则2p≡1 (modq)。因为p是素数,可知域Zq的乘法群Zq\{0} 中元素2 的阶是p。 该群有q-1 个元素。 根据Lagrange 定理,我们知道每个元素的阶整除该群的元素个数,即我们有p |(q-1)。 从而有p 教学过程中可以更加注重讲解Mersenne 数和素数的联系及其相关性质,让学生更加深入运用Mersenne 数有关性质,同时也能运用更多相关知识解决问题,可以作为Euclid 证明法的扩展教学,让有较强能力的同学理解较难的证明法,达到拓展能力的目的。 素数及其无穷性质的一些性质可以使用电脑编写程序,进行模拟实验,可以对应不同层次的学生设计不同的素数无穷性质证明相关的实践教学,帮助学生深入理解和掌握素数及其无穷性质的相关性质。 大学工科学生编程和实践能力相对较强,可以指导其设计和验证程序,对数进行是否为素数的判断,进而进行实践,设计算法生成素数。 可以进行以下实验: 实验名称:素数的判断与生成和遍历素数尝试。 实验内容:使用编程语言实现素数的判断,并且生成素数表,最后尝试遍历素数。 实验步骤: (1) 掌握素数及其无穷性质和相关性质; (2) 编写函数实现素数的判断; (3) 编写程序实现素数表的生成; (4) 优化程序,使程序在有限时间内尽可能生成更多素数,体会素数无穷性; (5) 继续优化和完善程序并思考。 实验思考:如何编写函数判断一个数是不是素数,如何通过程序生成素数,如何生成更多,更大的素数。 注意:教学时将重点放在素数无穷的性质上,可以引导学生生成较大素数,感受素数无穷的性质。 可以先假设素数有限,让学生通过Euclid 法尝试生成素数,然后通过实验推翻此假设,从而达到素数无穷性的教学目的。 对工科学生的教学应该将重点放在实践方面,让学生实实在在感受素数及其性质,深入理解素数的无穷性质及运用。 大学理科学生理论知识较好,可以指导其设计算法,验证素数无穷性质的Euclid 证明法。 可以进行以下实验: 实验名称:素数无穷性质证明的程序验证和素数相关规律讨论。 实验内容:使用编程语言实现素数无穷性质证明的程序验证。 实验步骤: (1) 掌握素数及其无穷性质和相关性质,掌握Euclid 证明法; (2) 编写程序,实现数的分解; (3) 编写程序,由小到大输出等式,对素数无穷性质进行验证; (4) 从实验中寻找素数及Euclid 法素数无穷性质证明相关规律; (5) 验证程序的正确性,优化完善程序。 实验思考:如何通过编程实现Euclid 证明法的验证。 图2 是本实验的一个可行输出结果: 图2 Euclid 证明法可行结果 注意:教学时将重点放在素数及其无穷性质的性质上,重点通过实验,直观地让学生感受Euclid 证明法及其证明的原理。 在对理科学生的教学中,以理论知识教学为重,将教学重点放在理解证明以及规律和方法上。 素数以及其无穷性质有非常广泛的应用,很多应用贴近生活,易于理解。 进行素数及其无穷性质的应用以及其教学,可以激发学生对素数及其无穷性质的兴趣,有助于其对素数及其无穷性质有更加深入的理解。 针对大学工科新生,可以使用较为贴近生活的应用场景进行教学。 可以举出素数以及其无穷性质在自然科学中的运用,以图片,案例为主,进行泛式讲述。 可以针对以下段落列出的相关材料展开进行讲述和教学。 素数在自然科学领域的运用极其广泛。 在汽车变速箱齿轮的设计上,相邻的两个大小齿轮齿数设计成质数,以增加两齿轮内两个相同的齿相遇啮合次数的最小公倍数,可增强耐用度减少故障。 在害虫的生物生长周期与杀虫剂使用之间的关系上,杀虫剂的质数次数的使用也得到了证明。 实验表明,质数次数地使用杀虫剂是最合理的:都是使用在害虫繁殖的高潮期,而且害虫很难产生抗药性。 以质数形式无规律变化的导弹和鱼雷可以使敌人不易拦截。 多数生物的生命周期也是质数(单位为年),这样可以最大程度地减少碰见天敌的机会。 诸如此类,素数在自然科学中的运用极其广泛,其无穷性质也在物理学等学科有着广泛的运用。 通过素数无穷性质的教学,可以让同学对素数有更深的认识,提高数学素养。 需要注意的是,进行教学时,不必深入讲解其内在原理,可以对其大致原因进行阐述即可。 主要目的是激发学生对素数以及素数无穷性质的兴趣,使其在后续学习生活中关注素数及其无穷性质的学习以及应用。 大学高年级学生,其数学基础较好,可以用稍复杂的,但应用十分广泛的案例进行应用教学。 可以使用RSA 公钥加密算法[8]作为案例进行应用教学。 在密码学中,公钥加密需要将想要传递的信息在编码时加入素数,编码之后传送给收信人,著名的非对称加密算法RSA 公钥加密算法就运用了大素数。 素数的选择一定程度上决定了加密的安全性。 素数的无穷性质证明为逼近无穷大的素数的存在性提供了证明。 通过运用素数的无穷性质,可以不断寻找大素数,使用不同的大素数进行加密,可以一定程度保证加密不易被破解,进一步提升其可靠性。 讲解RSA 公钥加密的过程[9]: (1) 设φ(n) 为n的欧拉函数的值[10],选择两个大素数p和q,并计算其乘积n=pq,则有以下等式:φ(n)=(p-1)(q-1) ; (2 ) 选择一个大整数e, 满足gcd(e,φ(n))=1,整数e用作加密密钥。 (3 ) 确定的解密密钥d, 满足(de) modφ(n)=1,即de=kφ(n)+1,k≥1 是一个任意的整数。 易知,若知道e和φ(n),很容易计算出d。 (4) 公开整数n和e,秘密保存d。 (5) 将明文m(m c=E(m)=memodn (6) 将密文c解密为明文m的算法为: m=D(c)=cdmodn 可以知道,只根据n和e要计算出d是非常困难的。 只有知道d才能进行解密。 通过学习RSA 加密的过程,可以理解到,RSA 加密的安全性大大依赖于大整数的分解[11]。 然而可以知道,由于素数的无穷性质,我们可以找到足够大的素数,这样也就保证了RSA 加密算法的安全性。 进行讲解时,讲解到学生理解加密过程即可,着重讲解素数及其无穷性质在RSA 加密中的作用。 讲解的目的着重在讲解素数应用的方面。 同时,若学生理解能力较强,还可以让学生进一步对RSA 加密进行实际操作,可以让有能力的学生编写程序实现RSA加密的主要过程,以达到应用教学的目的。 再分别用Nb和Ns来记不超过N的自然数中至少有一个大素数因子和只有小素数因子的自然数个数。 将可以证明,对适当的N有 Nb+Ns 但按定义应有Nb+Ns=N,从而导致矛盾。 本文针对不同阶段和专业类型大学生,提供了素数无穷性质证明的分层次教学设计,旨在让更多学生更加深入理解素数及其无穷性质的相关知识和性质。 了解和学习素数的无穷性质证明,可以让学生深入理解素数,加强学生的数学素养,培养学生的逻辑思维能力。 素数及其无穷性质在各大领域都有广泛运用,在未来的应用或将更加广泛,对更多人进行相关教学具有相当的重要性。 进行案例化教学时,着重讲述证明过程和证明思想,以生动的讲解,清晰地证明素数的无穷性质。 应该对于不同的教学对象采用不同的教学方法,做到因材施教。 教学中要避免使用过于困难的材料,引用已有定理时确保学生都能够理解,尽量让教学生动易懂,同时激发学习兴趣,让更多人了解素数及其无穷性质的证明和相关性质及应用。3.2 针对大学理科新生的教学设计
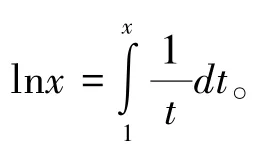
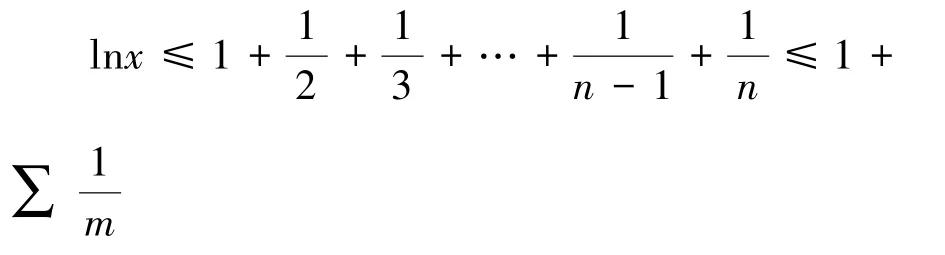
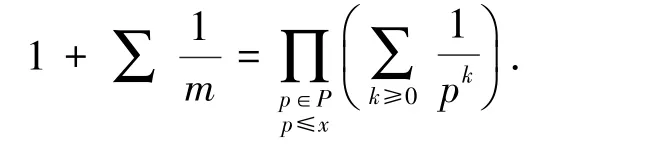

3.3 针对大学本科高年级学生的教学设计
3.4 针对大学研究生的教学设计
4 素数无穷性质证明的分层次实践教学设计
4.1 针对大学工科学生的素数无穷性质的实践教学设计
4.2 针对大学理科学生的素数无穷性质的实践教学设计
5 素数无穷性质应用的教学设计
5.1 针对大学新生的素数无穷性质应用的教学设计
5.2 针对大学本科高年级学生的素数无穷性质应用的教学设计
5.3 针对大学研究生的素数无穷性质应用的教学设计
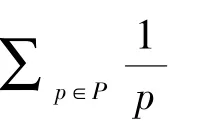



6 总结
