游戏中的数学
2021-07-15陈燕娜
陈燕娜

【摘要】本案例以游戏——掷骰子为主线,设计了三个不同层次的试验,举行了三次有意义的举牌活动,让学生在游戏中收获知识,在活动中检验知识。本课的中心环节通過设置问题,让学生提出猜想;通过发现问题,推动学生深入猜想;在解决问题中使学生的猜想得到验证。整节课,掷骰子的数学游戏贯穿始终,学生的逻辑思维能力会在这个过程中逐步得到提升。另外,当学生发现生活中随处可见的骰子竟然也可以是数学课的素材,使平凡的事物展现了不平凡的魅力,他们就会慢慢转变看待数学、看待生活的眼光,学习数学的兴趣便会愈发浓烈。
【关键词】掷骰子;数学游戏;试验;点数和;可能性
一、问题的提出
综合与实践是小学数学教学中的一个重要领域,也是小学数学教材内容的一大亮点。综合与实践课以数学学科为主要阵地,融合其它学科知识及与学生密切相关的现实生活情境。《义务教育数学课程标准(2011年版)》(以下简称《标准》)再次强调,要充分发挥“综合与实践”,帮助学生积累数学活动的经验,培养学生的应用意识和创新意识等方面的重要作用。然而,当前的小学数学综合与实践教学现状并不理想,令人堪忧。主要表现在:
1.综合与实践课内容多以活动为载体,部分学校开展实践活动的条件有限,加之需要准备很多教具和学具,以及要完成相关的调查实验,大多数教师对于此类课程实施热情不高。
2.综合与实践课不作为学业水平的考查目标,在以知识和技能量化评价的测试卷中不占一席之地。教师在常态教学中或简单提一提,或让学生作为课外拓展材料自主学习。
反思综合与实践课的教学现状,作为小学数学教材的一个重要板块,它不是可有可无,而是数学教育教学本质的必然回归。近几年,花都区对小学数学的考查逐步渗透了综合与实践课程的内容。这说明花都区的教研方向更加紧扣《标准》,更加明确了在综合与实践活动中培养学生的综合能力和创新意识。因此,开展小学数学综合与实践课程研究具有重要的意义。
如何让学生和教师都爱上综合与实践课?笔者认为,活泼、好动、爱玩是小学生显著的心理年龄特征,他们容易被有趣生动的游戏深深吸引。如果数学综合与实践课堂变成一场有趣的游戏,那么,小学生就会对数学综合与实践产生浓厚的兴趣,并且爱上数学。如果我们能探索出一套切合本校实际的、行之有效的小学数学综合与实践课程的途径与策略,教师也会乐于上综合与实践课。基于这样的设想,笔者提出将游戏化教学应用到小学数学综合与实践课程。
二、教材分析
《掷一掷》是小学数学“实践与综合应用”部分的内容,它是在学生学习了可能性、组合等有关知识的基础上,以游戏形式探讨“可能性的大小”的实践活动。本节课“可能性”的知识相对抽象和枯燥,学生理解起来有一定的难度。但是,孩子天生就有在游戏中学习的本领,而且骰子在我们的生活随处可见。学生也在课余时间经常利用“掷骰子”来玩飞行棋等有趣的游戏。结合教材和学生实际,笔者将掷骰子这个游戏融入本节课的教学,意在让学生经历观察、猜想、试验、验证的过程,巩固“组合”的有关知识,探讨事件发生的可能性大小。
基于对教材和学情的分析,笔者将本节课的教学目标定位如下:
1.经历观察、猜想、试验、验证的学习过程,综合运用所学知识来探讨事件发生的可能性大小。
2.结合实际情境,培养提出问题、分析和解决问题的能力。
3.通过应用和反思,积累数学活动经验,感受成功的体验,提高学习数学的兴趣。
其中“探讨事件发生的可能性大小”是本课教学的重点,难点在于综合运用所学知识来解决问题。
为了突破教学的重难点,笔者设计了以下的教法和学法(见图1),其中以游戏教学法作为主要的教法,以实践活动法为主要的学习方法。
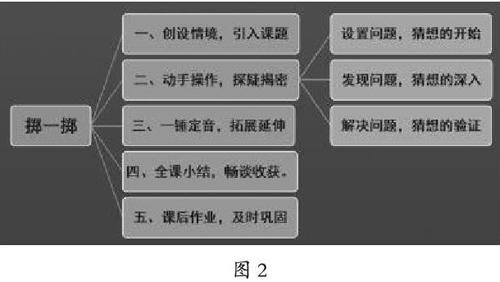
基于以上分析,笔者将本课的教学环节定位为以下几方面(见图2),其中第二个环节——“动手操作,探疑解密”是重点环节。
三、教学实践
(一)创设情境,引入课题
师:同学们,看过足球赛吗?
生:看过!
师:那请看课件,裁判正在做什么?
(出示课件,学生七嘴八舌抢答)
师:哦!他正在抛硬币决定谁先开球呢!
师:同学们,抛硬币这个游戏公平吗?
(设计意图:这个问题是学生学习的起点,它使学生从观看足球赛的心情自然地过渡到数学的探索和研究中来,并且带出了游戏背后的内涵——可能性)
到底这个游戏公平吗?学生们很快会联想起本单元学习过的内容——由于硬币抛出正反两面的可能性是相同的,所以这个游戏是公平的。
笔者又问:那生活中像这样公平做出选择的游戏还有吗?
学生们又想起了石头、剪刀、布、掷骰子等等。
师:那同学们,你们玩过掷骰子的游戏吗?
生:玩过!
师:那谁来介绍一下?
(设计意图:这里通过学生的介绍,唤起了学生的生活经验,也为笔者接下来设计的探究活动奠定了基础)
(二)动手操作,探疑揭密
笔者出示两个骰子,提出这样一个问题:同时掷两个相同的骰子,把两个朝上的点数相加,“和”有哪些情况?
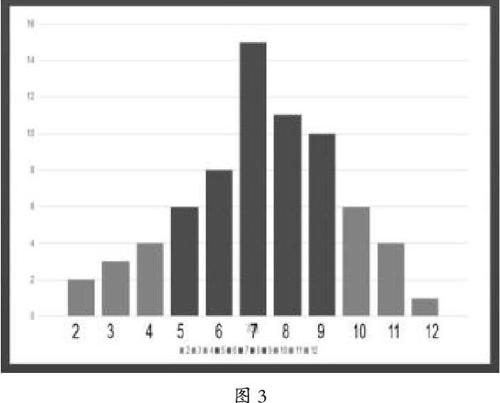
笔者根据学生的回答板书了2、3、4、5、6、7、8、9、10、11、12这11种情况。
紧接着,笔者又提了一个问题:两个骰子的点数和有可能是1和13吗?
在学生们的交流和讨论中,学生们明确了两个骰子的点数和不可能是1和13,这个是确定的,只可能在2-12之间,这个是不确定的。
(设计意图:这个环节让学生进一步理解事件发生可能性与事件确定性的紧密联系)
1.设置问题,猜想的开始
笔者出示游戏规则:同时掷两个相同的骰子,如果掷出的点数和是5、6、7、8、9则红队赢,如果掷出的点数和是2、3、4、10、11、12则蓝队赢。