尺寸关联更改传播路径生成方法

杨 波 尚俊芝 马 宁 高常青

济南大学机械工程学院，济南，250022

0 引言

工程更改的传播会导致开发过程中的复杂性和风险增加、成本提高[1-2]。复杂产品在尺寸、结构等属性方面往往存在着多尺度的关联，其中任一属性发生的设计更改，不仅会触发相关零件结构上的连锁关联更改，而且也会引发相关尺寸参数的一系列变更传递。鉴于尺寸更改的广泛性与复杂性，有必要对其传播过程进行描述与分析。

目前，针对尺寸更改传播的研究主要包括尺寸关联设计和更改传播路径两个方面，两者存在很强的依赖性。

关联设计是准确预测更改传播的关键。针对关联设计中存在的关联传递、关联耦合等问题，目前的解决方法主要有基于骨架模型的关联设计方法[3]、基于产品族模块组合的主从关联设计方法[4]、基于设计结构矩阵的关联解耦策略[5]、基于关联的变更操作算法[6]等。以产品关联设计理论为基础，尺寸关联设计是在参数化设计技术的基础上，通过建立尺寸约束以及特征参数的多参数关联关系来完成对变更传播的影响分析。刘振宇等[7]运用灰熵关联分析对特征关联参数进行筛选，研究了多个特征参数关联对复杂产品性能的影响；徐新胜等[8]采用事物特性表技术，基于尺寸关联设计模型，实现了产品自顶向下的变型设计；彭翔等[9]通过定性分析设计变量与性能目标间的关联关系，构建了精确的复杂产品整体性能关联模型；BAUDOUI等[10]利用后发式局部不确定传播分析方法，减少了参数不确定性对性能的影响。更改传播路径的搜索是尺寸更改传播研究的重要分支，有效的关联路径搜索算法是解决尺寸更改传播效率问题的重要手段，目前常见的方法主要有基于关联网络的方法和基于设计结构矩阵的方法。杨帆等[11-12]建立了基于公式量化表达的产品参数关联网络模型，研究了更改传播路径的搜索算法；MA等[13]通过在参量关联网络图上增加关联强度属性，并以关联影响最低为目标，提出了最优更改传播路径搜索算法；陈进平等[14]、刘彦臣等[15]以关联网络为基础，分别采用深度及广度优先算法，实现了关联传播范围的求解和可行更改路径的优选；TANG等[16-17]用设计结构矩阵描述产品的结构关联，确定了工程变更传播及影响范围，提出了变更传递路径的搜索算法；宫中伟等[18]以设计结构矩阵为基础，提出了基于联系依赖矩阵的工程变更雪崩传播预测方法；CLARKSON等[19]提出了基于非布尔型设计结构矩阵的变更预测算法。

上述工作为基于关联的尺寸更改传播研究提供了可靠的理论基础，但目前相关研究主要集中于产品结构更改的传播以及参数变更对产品性能影响等方面。如何基于产品结构的层次与逻辑关系，研究尺寸特性的定量转变方式和更改传播的转化特性，使得计算机技术能以更为有效的方式为设计自动化服务，是该领域面对的深层问题。

针对上述问题，本文进行了尺寸关联更改传播路径生成方法的相关研究。为有效描述尺寸特性间的逻辑与层次关系，建立了由尺寸逻辑元、更改传播逻辑元、尺寸更改传播系数组成的关联更改传播模型，提出了基于零件关联的尺寸更改传播路径识别与优选方法，给出了基于内积运算的尺寸关联更改传播路径搜索算法，确定了更改尺寸在产品中的传播过程与路径。该方法从关联角度描述了尺寸的关联与传递关系，为工程更改传播提供了尺寸特性更改传递的定量转变方式。

1 尺寸关联更改传播模型的构成要素

更改传播路径借由零件间的多种关联关系来表征。作为装配结构的固有属性，零件间的关联关系具有多维性和复杂性等特点，零件自身的尺寸特性、相关零件的尺寸关联特性以及尺寸关联波动的强弱程度在尺寸传播更改过程中具有关键的作用。为有效描述尺寸特性间的逻辑与层次关系，以尺寸逻辑元、更改传播逻辑元、尺寸更改传播系数作为尺寸关联更改传播模型的构成要素。

1.1 尺寸逻辑元

在尺寸更改设计迭代过程中，尺寸逻辑元是由零件(或组件，为简化描述本文统称为零件)的基本信息构成的基本单元，它也是尺寸关联更改传播的基本单元。通过尺寸逻辑元可以实现能量转化、转移，并完成尺寸更改的传递。图1所示为尺寸逻辑元的一般化符号模型。

图1 尺寸逻辑元模型Fig.1 Logical unit model of dimension

图1中，Pi表示第i个零件；E(Pi)表示零件Pi的一组尺寸参数，主要是指工程更改发生时，零件Pi发生关联变更的物理特性尺寸、几何结构尺寸等；ai，j为零件Pi的第j个尺寸参数。定义

E(Pi)= {ai，1，ai，2，…，ai，n}

其中，n为零件Pi中发生关联变更的尺寸参数数量(即集合E(Pi)中元素的数量)，并定义

EC(Ps，Pi)={ai，k1，ai，k2，…，ai，kt}

其中，EC(Ps，Pi)表示在更改传播中当零件Pi更改时，对零件Ps尺寸参数产生影响的Pi的尺寸参数集合。ai，kt为会对零件Ps尺寸参数产生影响的零件Pi的第kt个尺寸参数，kt≤n，t为集合EC(Ps，Pi)中元素的数量，且有

EC(Ps，Pi)⊆E(Pi)

有向线段表示零件之间的尺寸关联更改传递流，该线段的方向代表更改的流向及因果关系，线段的主要状态参数包括尺寸变量的类型、大小和路径，线段的特征值为尺寸更改传播系数λ。

1.2 更改传播逻辑元

相关联零件之间的功能和结构连接关系(如尺寸特性之间的配合关系、输入与输出特性之间的匹配关系等)决定了设计更改从一个零件向另一个零件的传播路径与方式。为简化更改分析，在梳理零件间复杂关联关系的基础上，基于尺寸更改传播的特点，建立了构成更改传播网络的基本单元——更改传播逻辑元，可分为如下三类。

(1)AND逻辑元。当某父代零件尺寸特性更改时，两个或多个子代零件的尺寸特性必须同时更改，其模型结构如图2a所示；当两子代零件形成AND逻辑关系时，这两个子代零件必然同时受其父代零件相同尺寸参数的影响，此时，EC(P2，P1) ∩EC(P3，P1)≠∅。

(2)OR逻辑元。当某父代零件尺寸特性更改时，两个或多个子代零件只需更改其中之一，如图2b所示，此时，EC(P2，P1) ∩EC(P3，P1)=∅；

(3)继承逻辑元。当子代零件完全继承父代零件的尺寸更改信息时，如图2c所示，此时，EC(P2，P1)=E(P1)。

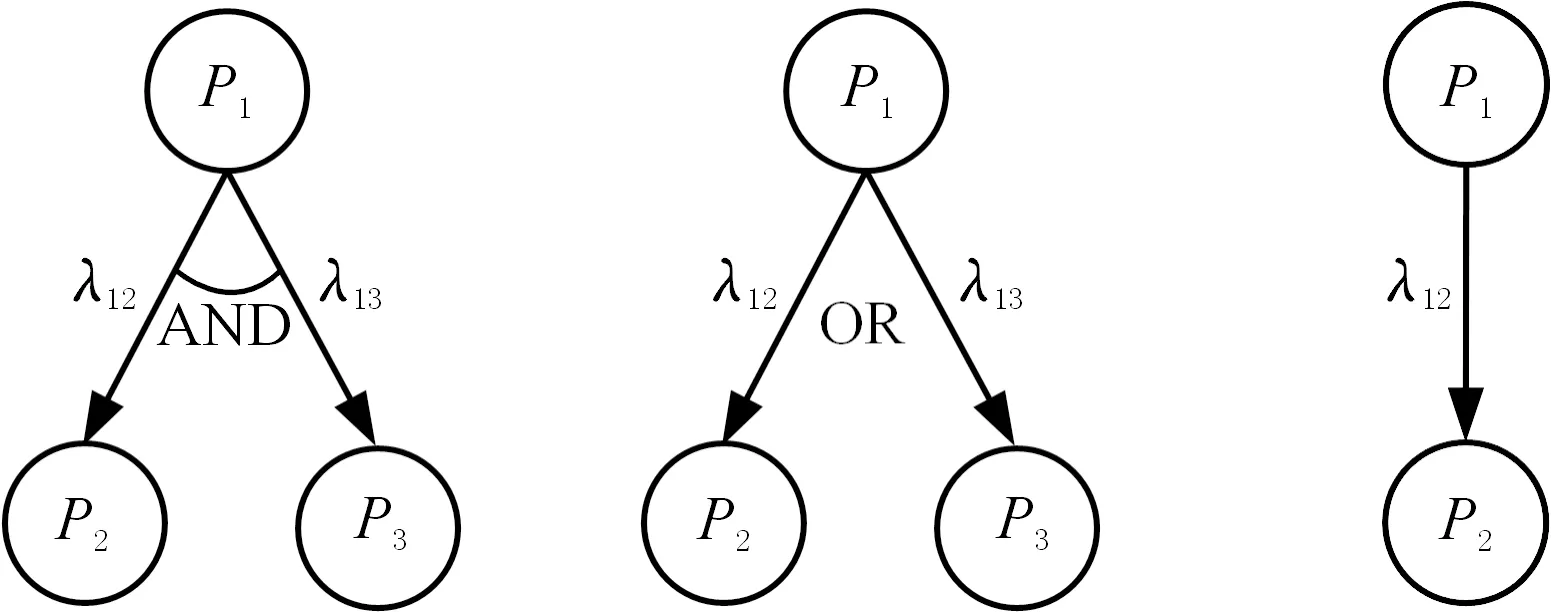
(a) AND逻辑元 (b) OR逻辑元 (c) 继承逻辑元图2 更改传播逻辑元模型Fig.2 Logic unit model for change propagation

1.3 尺寸更改传播系数

在尺寸关联模型中，设计更改引发的波动是通过零件特性之间的连接对象进行传播的，不同的连接关系对其特性的约束程度是不同的，其传播更改的能力也存在差异。在此引入尺寸更改传播系数来表征这种差异。

尺寸更改传播系数λis用于表征父代零件Pi的尺寸更改对子代零件Ps尺寸的关联影响程度。当仅考虑更改传播逻辑元为AND和OR情况时，定义

(1)

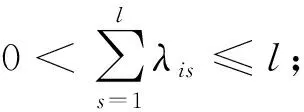
2 尺寸关联更改传播路径规划

识别可能的更改传播路径是进行更改传播分析的一项重要前提。为简化路径搜索过程，本文采用从零件到尺寸的分层次路径搜索方法。利用矩阵描述尺寸特性之间的关联关系，基于逻辑运算识别它们之间的逻辑关系，并建立以零件为节点和以尺寸为节点的关联更改传播路径，从而将工程更改影响分析中尺寸更改传递问题转化为关联矩阵运算问题。

由于在路径搜索的不同阶段涉及到不同的关联矩阵，为方便运算，给出如下定义：

定义1 零件尺寸与零件间关联矩阵：该矩阵基于尺寸特性之间的逻辑关系而形成，用以描述会对相关零件的尺寸参数产生影响的更改零件尺寸参数的情况。

定义2 尺寸关联矩阵：用于描述相关零件尺寸特性之间关联关系的矩阵。

零件尺寸与零件间关联矩阵、尺寸关联矩阵分别以零件、尺寸为目标对象，并分别用于建立以零件为节点和以尺寸为节点的更改传播路径。

2.1 以零件为节点的更改传播路径

2.1.1更改传播路径的初选

尺寸更改传播发生的根本原因是产品内部零件尺寸之间存在相互关联关系，因此，在更改传播路径初选的过程中，以零件为节点，依据零件之间的尺寸关联关系建立更改传播路径并进行优选。具体步骤如下。

(1)建立产品关联零件集合P={Pi}。

(2)建立尺寸逻辑元模型，并确定各零件的关联更改尺寸参数集E(Pi)= {ai，1，ai，2，…，ai，n}。如有4个零件组成的装配体，根据其尺寸关系可建立其尺寸逻辑元模型，如图3所示。

图3 尺寸逻辑元模型(示例)Fig.3 Dimension logic unit model(example)

(3)建立零件尺寸与零件间的关联关系表征模型。主要包含如下几个步骤：

第一步，建立零件间的关联集值矩阵。根据所有参与关联更改的零件间的尺寸关联关系，以集合EC(Ps，Pi)为基础，建立关联集值矩阵R=[rsi]。该矩阵以零件为载体，通过建立会对相关零件尺寸参数产生影响的更改零件的尺寸参数集合来构建零件之间的关联关系，其中

矩阵R中第s行第i列元素rsi表示对受影响零件Ps尺寸参数产生影响的更改零件Pi尺寸参数集合。为便于处理，规定矩阵中行零件与列零件的排序相同。以图3为例，假设其关联集值矩阵R如表1所示，表中元素为与行零件Ps的尺寸参数存在关联关系的列零件Pi的尺寸参数集合。例如，由表1中第一行、第二列元素可知，列零件P2的尺寸参数a2，1、a2，2会对行零件P1的尺寸参数产生关联影响。

表1 零件间的关联集值矩阵

第二步，建立中间转换矩阵。将矩阵R的列由零件扩展为该零件的尺寸参数，同时对矩阵R进行二进制转化，用“1”、“0”分别表示列尺寸参数“是”或“否”会对行零件的某一尺寸参数产生影响，进而建立中间转换矩阵，如表2所示。

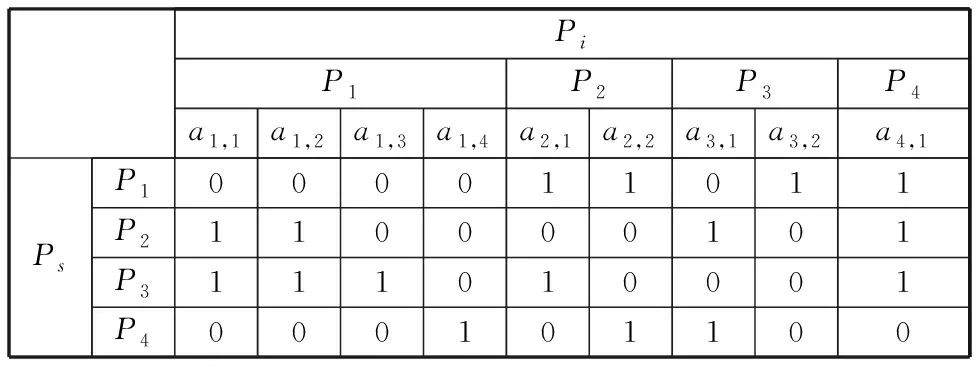
表2 中间转换矩阵

第三步，建立零件尺寸与零件间的关联矩阵。为便于运算，将中间转换矩阵转化为向量值矩阵C=[csi]l×l，其中csi为二进制向量，可表征对受影响零件Ps尺寸参数产生影响的更改零件Pi的尺寸参数情况，l为相关零件的数量。该矩阵更为直观地描述了更改零件的尺寸参数对其余零件的影响。将表2所示的中间转换矩阵转换为向量值矩阵，可表示为

(4)根据是否被共同的父代零件尺寸参数所影响来确定子代零件之间的逻辑关系。若选取矩阵C中第i列零件Pi为更改零件(即更改源)，则对该列所有的非零向量两两进行“与”操作，根据“与”操作结果可以识别子代零件是否被共同的父代零件的尺寸参数所影响。本文采用“&”代表“与”操作运算符，对于零件Ps、Pm，若csi&cmi≠0(i≠m≠s)，则零件Ps与Pm之间的逻辑关系为AND，否则两者之间形成OR关系；对于多个零件Pm、Ps、Pa、Pb，若(csi&cmi)&(cai&cbi)≠0(i≠m≠s≠a≠b)，则这些零件之间的逻辑关系为AND，否则为OR关系。上述图3示例中，以列零件P1为父代节点，即以表1所示的矩阵R中第一列为更改源，以该列中的非零向量所对应的行零件为子代节点，依据上述方法可确定零件之间的AND、OR逻辑关系，进而可建立以零件为节点的第一层更改传播路径，如图4所示。

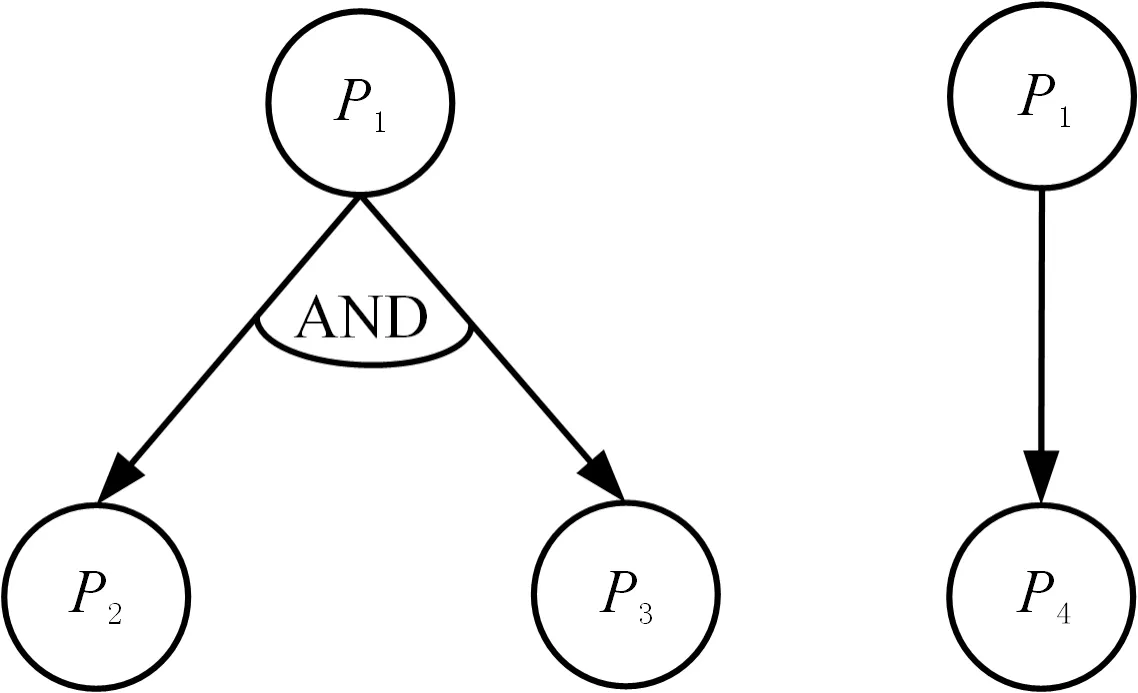
图4 第一层更改传播路径(示例)Fig.4 First level change propagation path(example)

(5)以第一层更改传播路径的子代节点为更改源，重复步骤(4)，进行迭代搜索。

(6)搜索终止条件的确定。一般情况下，更改是单向的(即尺寸的更改不形成闭环反馈)，因此在搜索过程中，当路径的某一分支中出现与父代节点相同的零件时，则搜索停止。在更改传播路径图中，为表达搜索过程的完整性，将终止节点用虚线圆表示，且该节点不计入传播路径。基于上述过程，可得到图3示例所示的以零件为节点的更改传播路径，如图5所示。

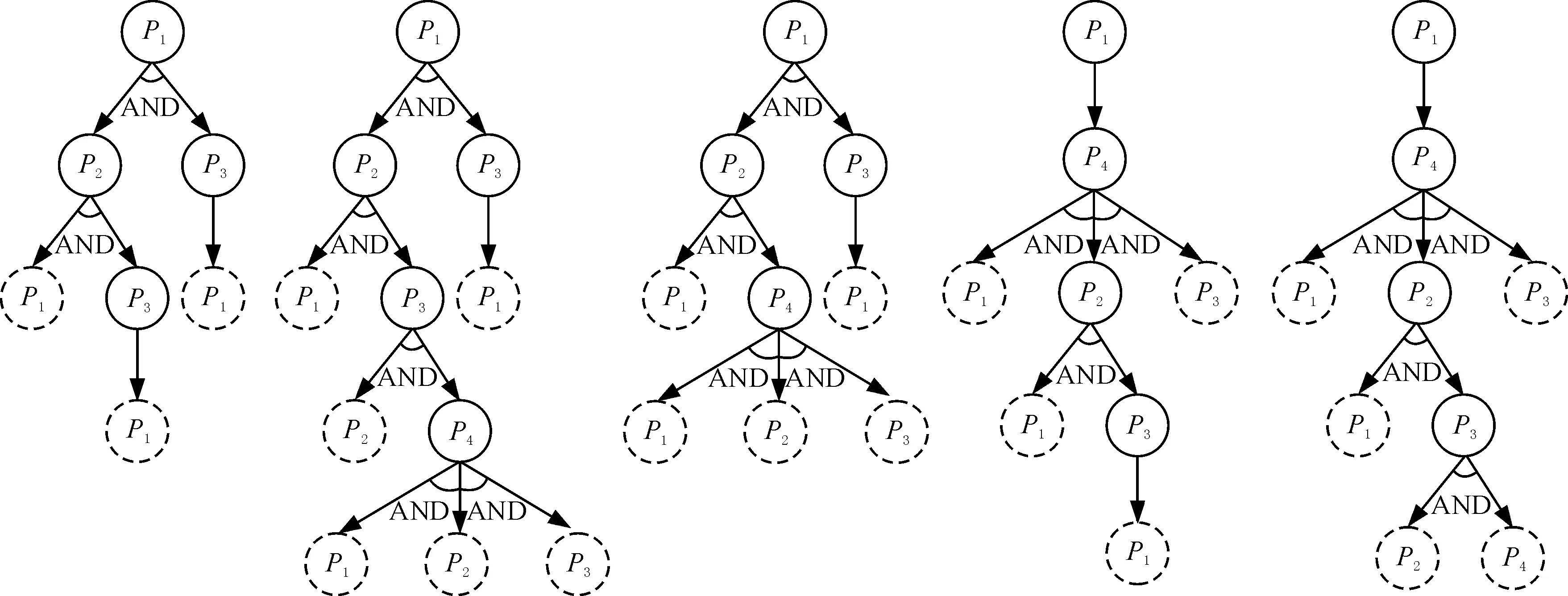
(a) 路径1 (b) 路径2 (c) 路径3 (d) 路径4 (e) 路径5图5 零件更改传播路径的初选(示例)Fig.5 Preliminary selection of part-based change propagation path(example)

2.1.2更改传播路径的优选

以零件为节点的更改传播会形成多条路径，如何从多条更改路径中选择一条经济可行的方案是工程变更传播需要解决的重要问题。路径的优选涉及到几何结构、配合关系、更改成本等多方面的内容，是个错综复杂的问题。本文仅从尺寸关联及其变更成本的角度考虑路径的优选问题。

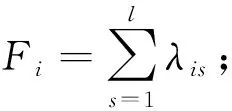
在不考虑其他约束条件的情况下，取评价指标值最小的路径为最终更改传播路径。

2.2 以尺寸为节点的更改传播路径

基于2.1节所描述的过程，可得到以零件为节点的更改传播路径。但在更改传播过程中，上层零件某一尺寸的更改并非直接反馈到下层相关零件的所有尺寸上，如何确定更改尺寸在零件确定尺寸间的传递过程与路径，是最终进行尺寸传播分析的基础。

内积运算的物理意义是一个向量在另一个向量上的投影，其运算结果可以说明两个向量在某一方向上的相互影响程度或接近程度。由此，本文以2.1节中所形成的零件间传播路径为基础，基于内积运算，提出了以尺寸为节点的更改传播路径搜索算法。

根据以零件为节点的更改传播路径，首先建立关联路径图上相邻父子节点零件Pm、Ps之间的尺寸关联矩阵为

D(Ps，Pm)=[duv]n1×n2

其中，n1为零件Ps的尺寸参数数量，n2为零件Pm的尺寸参数数量；在矩阵D(Ps，Pm)中，若零件Pm的第v个尺寸会对零件Ps的第u个尺寸产生影响，则duv=1，否则duv=0，在具体操作中，该矩阵可通过对建模软件中特征尺寸之间关系的识别获取。

为找出零件Pm的第v(1≤v≤n2)个尺寸所影响的零件Ps的尺寸参数集合，将ev与矩阵D(Ps，Pm)中的各行向量做内积运算，其中ev为内积运算算子，且ev为第v位为“1”的n2维单位向量；若ev与矩阵D(Ps，Pm)中第u(1≤u≤n1)行向量内积运算结果为1，则表明Pm的第v个尺寸参数会对Ps的第u个尺寸参数产生关联影响。

以图5b所示的路径为例，采用上述内积运算方法即可建立以零件P1中尺寸参数a1，1为初始更改尺寸的尺寸传播路径，如图6所示，具体步骤如下。

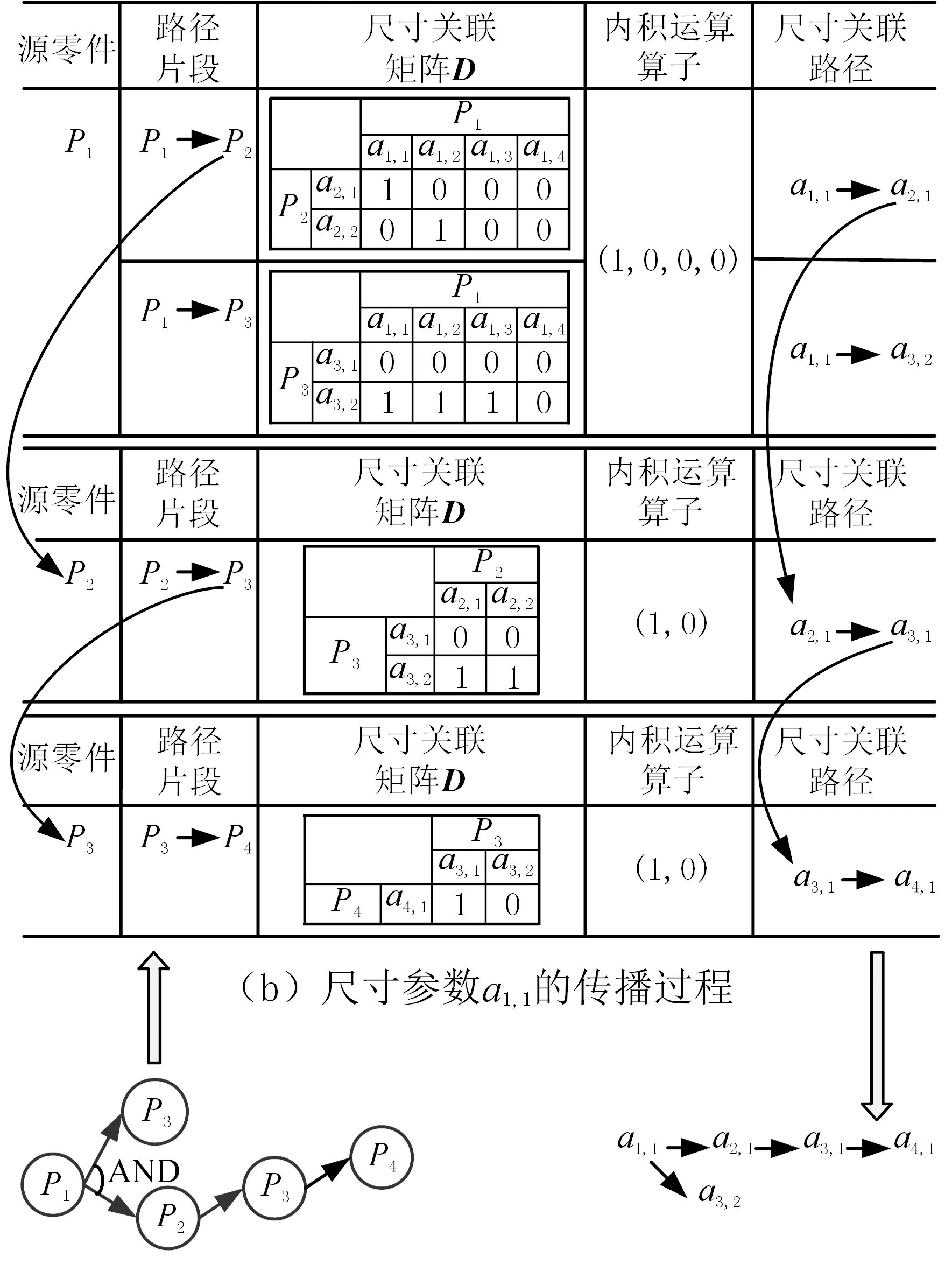
(a) 基于零件的更改 传播路径 (c) 尺寸a1，1的更改 传播路径图6 尺寸参数a1，1的传播路径分析Fig.6 Analysis of the propagation path of a1，1

(1)删除图5b所示路径的冗余节点，获取简化后的以零件为节点的传播路径，如图6a所示。

(2)基于图6a所示的以零件为节点的传播路径，分解出路径片段；建立第一段路径片段，即源零件P1与其子代零件P2、P3的尺寸关联矩阵D(P2，P1)、D(P3，P1)。

(3)初始变更尺寸a1，1为零件P1中4个尺寸分量的第一个分量，其内积运算算子为e1=(1，0，0，0)；将向量e1与矩阵D(P2，P1)、D(P3，P1)的各个行向量分别做内积运算，得到尺寸a1，1所影响的零件P2、P3的尺寸分别为a2，1、a3，2，由此可得第一段尺寸传递路径，即a1，1→a2，1，a1，1→a3，2。由图6a可知P1→P3路径终止。

(4)以零件P2为更改源，建立路径片段P2→P3的尺寸关联矩阵D(P3，P2)；依据尺寸a2，1在零件P2尺寸分量中的位置，将向量(1，0)与矩阵D(P3，P2)的各个行向量分别做内积运算，得到尺寸a2，1所影响的零件P3的尺寸为a3，1。

以此类推，可完成以尺寸a1，1为更改源的传播路径，如图6c所示。

3 实例

本节以覆膜机为例说明上述方法的应用。图7所示为覆膜机的结构模型。在工作过程中，送料机构对纸张进行运输，然后由吸料部件将纸张吸起并传递到皮带线1，由皮带线1运送至覆膜卷处进行压膜，压好膜的纸张继续传递到裁剪部位进行裁剪，最后经过皮带线2完成覆膜。

图7 覆膜机结构模型Fig.7 Structural model of laminating machine

为简化分析过程，本文只选取以图8所示的机架结构、吸料部件与送料机构三个部件所构成的装配体为例，分析尺寸更改传播过程。

该装配体中各零件的结构尺寸如图8所示，图中带有箭头的曲线表示零件之间存在装配关联关系。其中，机架P1与零件P3、P5、P7、P9、P10存在配合关系，气缸安装底板P2与零件P3、P4、P5存在配合关系，吸盘支架P8与零件P4、P6存在配合关系。各零件的关联尺寸参数如下：

E(P1)={a1，1，a1，2，a1，3，a1，4，a1，5}

E(P2)={a2，1，a2，2}E(P3)={a3，1}

E(P4)={a4，1，a4，2，a4，3}E(P5)={a5，1，a5，2}

E(P7)={a7，1，a7，2}E(P8)={a8，1，a8，2}

E(P9)={a9，1，a9，2，a9，3}E(P10)={a10，1，a10，2}

图8 覆膜机尺寸及装配关联关系Fig.8 Dimension and assembly relationship of laminating machine

3.1 以零件为节点的更改传播路径

首先建立零件尺寸与零件间的关联矩阵。根据零件间的尺寸关联关系，建立基于尺寸关联的覆膜机中间转换矩阵，如表3所示。

表3 覆膜机中间转换矩阵

然后确定子代零件之间的逻辑关系。为简化描述过程，将其中一个零件作为更改源，并描述其更改传播过程。在实际生产中，某一型号的覆膜机只能对特定尺寸范围的纸张进行加工，当纸张尺寸变化超过该范围时，则需要对覆膜机进行更改设计。由于纸张尺寸会对机架结构尺寸产生直接影响，因此将机架结构作为更改源。抽取表3中机架P1这一部分建立以机架为更改源的中间转换矩阵，如表4所示。

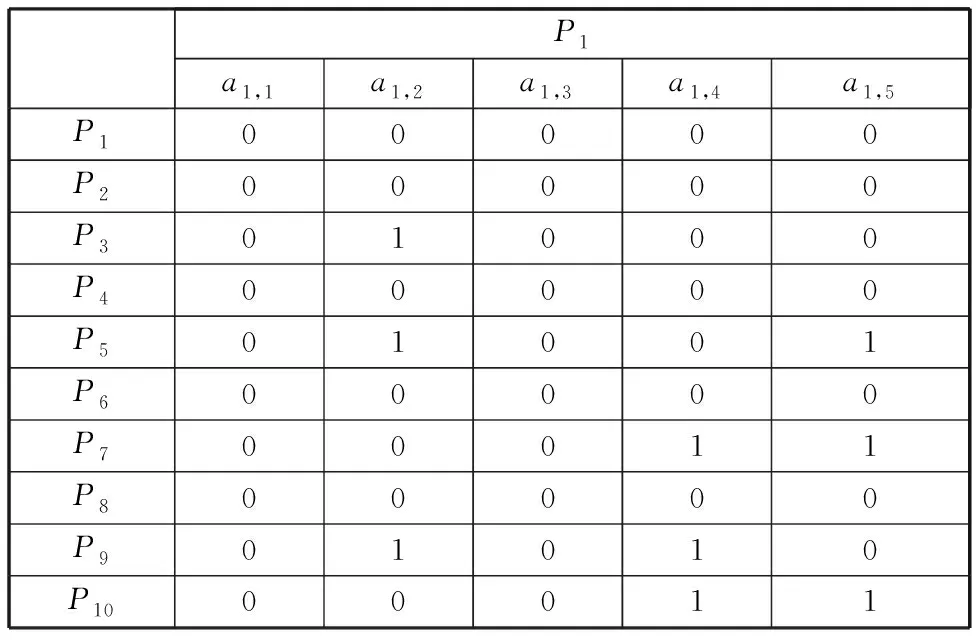
表4 机架作为更改源的中间转换矩阵

在表4所示的矩阵中，零件P3、P5、P7、P9及P10所在的行向量非零，这些零件为受零件P1更改影响的零件，并对该矩阵的这些非零行向量两两进行“与”操作，有

P3&P5=(0，1，0，0，0)P7&P10=(0，0，0，1，1)

P7&P9=(0，0，0，1，0)P9&P10=(0，0，0，1，0)

均为非零向量。由此可得到零件间的更改传播逻辑关系，见表5，其中，“A”、“O”分别代表零件之间的逻辑关系为“AND”、“OR”。

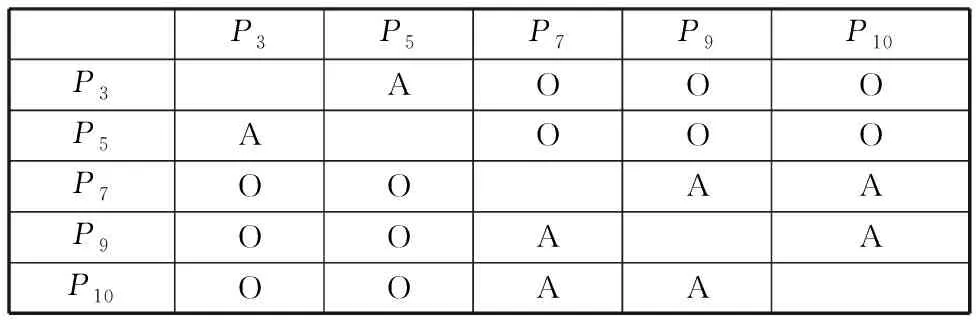
表5 零件间的更改传播逻辑关系

依据表5可建立第一层更改传播路径，如图9a所示。基于该路径中的“OR”关系，第一层路径可分解为两个子路径：①路径1′为P1→(P3，P5)；②路径2′为P1→(P7，P9，P10)。

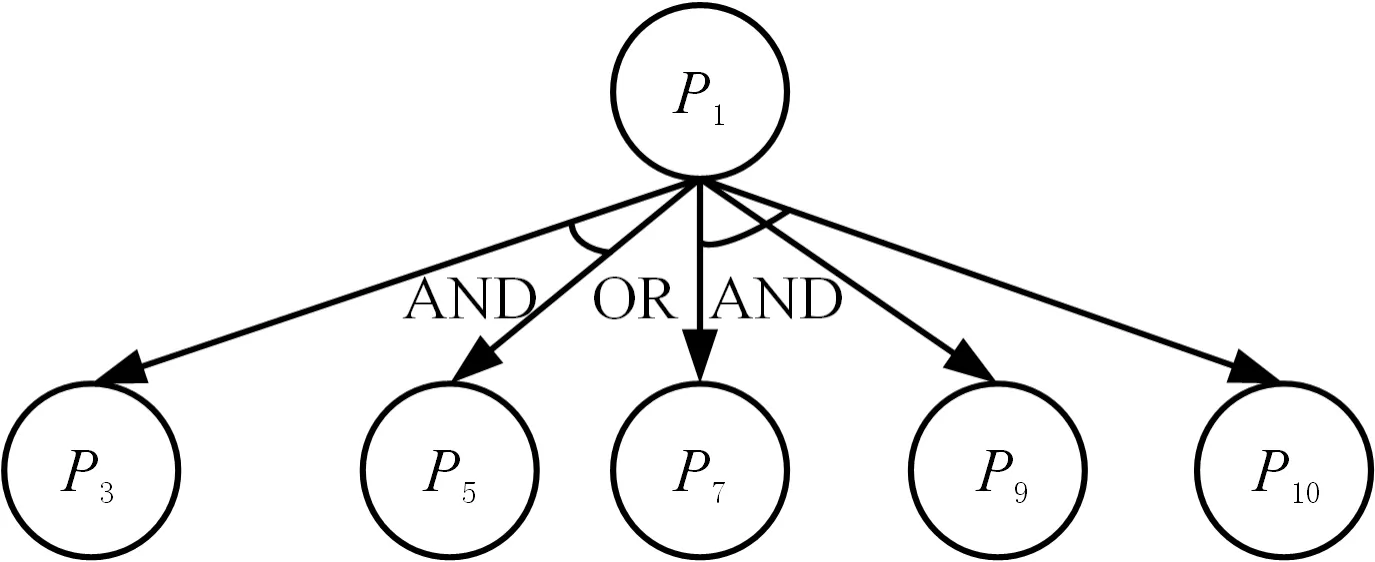
(a) 第一层路径

将路径1′中的P3、P5和路径2′中的P7、P9、P10分别作为下一层更改源，重复上述运算，可得最终基于零件的更改传播路径：路径1和路径2，如图9b所示。

3.2 以尺寸为节点的更改传播路径

建立关联路径图上父代零件与其子代零件的尺寸关联矩阵，分别如表6～表14所示。

表6 零件P1与零件P3尺寸关联矩阵

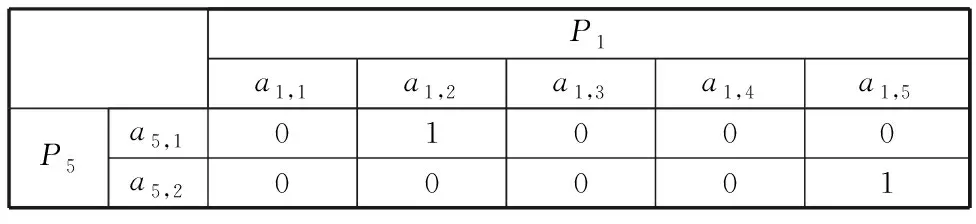
表7 零件P1与零件P5尺寸关联矩阵

表8 零件P1与零件P7尺寸关联矩阵

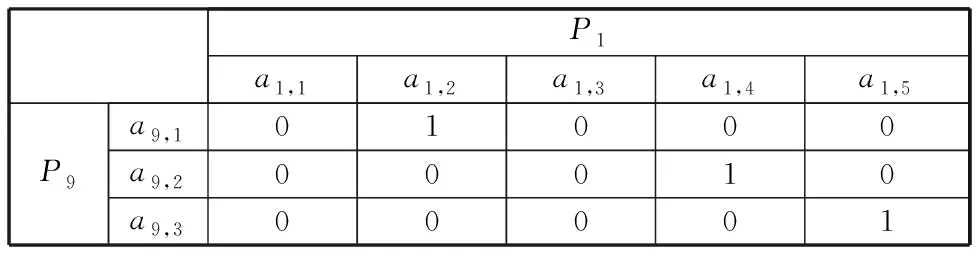
表9 零件P1与零件P9尺寸关联矩阵

表10 零件P1与零件P10尺寸关联矩阵

表11 零件P5与零件P2尺寸关联矩阵

表12 零件P2与零件P4尺寸关联矩阵

表13 零件P4与零件P8尺寸关联矩阵

表14 零件P3与零件P2尺寸关联矩阵

利用内积运算的方法，建立基于尺寸关联的传播路径。如在路径1中，父代零件为P1，子代零件分别为P3、P5，为求取尺寸a1，2的传播路径，可用向量(0，1，0，0，0)分别与表6和表7所示的矩阵中各个行向量做内积运算，可以得到零件P1中尺寸a1，2更改时的尺寸传播路径；同理也可得到零件P1中其他尺寸的传播路径。图10所示为最终基于尺寸的更改传播路径。

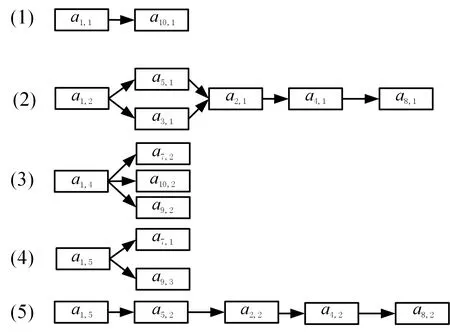
图10 最终尺寸传播路径Fig.10 Final dimension propagation path

4 结论

(1)建立了以尺寸逻辑元、更改传播逻辑元、尺寸更改传播系数为基本构成的关联更改传播模型，实现了尺寸特性之间层次与逻辑关系的精准描述。

(2)分别采用矩阵运算及向量内积运算方法，建立了以零件为节点和以尺寸为节点的关联更改传播路径，确定了更改尺寸在产品零件中相关尺寸间的传递过程与路径。这种基于矩阵的分析方法，一方面实现了尺寸关联关系由语义描述到数值描述的量化转变，另一方面基于数学运算的更改传播路径搜索方法使得该方法更便于计算机表达与实现。此外，采用从零件到尺寸的分层次路径搜索方法可显著降低搜索的复杂性，从而提高了搜索效率。

本文所提出的方法可为深入研究尺寸更改传播的内在机理提供一定的参考。但目前仅讨论了单个零件发生尺寸变更后其更改传播路径的搜索方法，对于多零件以及多参数耦合更改方面的研究还有所欠缺，这也将是后续研究工作中拟进一步讨论的问题。