基于有限元法带边型声子晶体结构的带隙研究
2021-07-15邓微陈晓宏
邓微,陈晓宏
(广州铁路职业技术学院,广州 510430)
0 引言
声子晶体[1]可分为Bragg和局域共振声子晶体两种不同结构形式,通过局域共振结构带隙产生的机理分析,在有限的空间里,只有用小于波长两个数量级的周期性结构才能在低频段产生带隙,即“小尺寸控制大波长”。本文通过在单层板上敷设等效“质量-弹簧”的局域共振子,获取较低的带隙起始频率和较宽的带隙绝对宽度,从而实现对500 Hz下的低频振动及噪声进行减振降噪控制。
1 带边型局域共振模型及材料参数
为研究单层板上添加局域共振子对低频振动特性的影响,建立合适的单板板附加共振子模型结构,如图1所示,其中晶格常数边长a=0.2 m,厚h为0.0025 m,软体层(橡胶阻尼块)A半径r2=0.05 m,厚度a2为0.01 m,具体参数如表1所示。图1是kx、ky方向完全对称的正方晶格,周期结构的第一和不可约布里渊区可用(如图2阴影部分)表示。

图1 带边型模型

图2 正方晶格

表1 局域振子材料
2 弹性波带隙计算
选择有限元法[2]对声子晶体的带隙特性进行研究。对声子晶体原胞结构进行参数设置、网格划分施加相应边界条件对结构进行后处理,就能得到特征频率和波矢之间的能带关系图。
2.1 有限元法及Bloch原理
对二维周期结构进行有限元法求解,特征值方程为
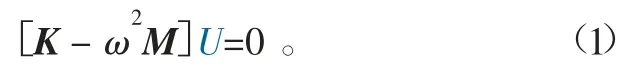
式中:K、M分别为周期共振子结构的刚度、质量矩阵;U为原胞结构的特征向量;ω为角频率。
根据布洛赫(Bloch)定理[3],沿x、y二维方向周期性结构位移场方程为
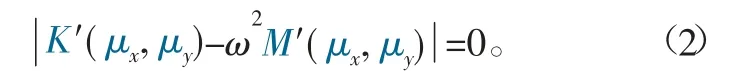
式中:K′、M′分别为二维周期共振子结构的刚度、质量矩阵;μ为波矢;μx、μy满足x、y二维方向周期性条件。
2.2 有限元法能带计算
利用有限元法沿x、y方向对波矢(k)布里渊区边界进行周期性扫描,选择Floquet周期性边界条件,在(-π/a,π/a)范围进行扫描。选取前10阶特征频率进行分析,可得到沿x、y方向周期性方向的能带结构图(如图3)和高对称点图(如图4)。
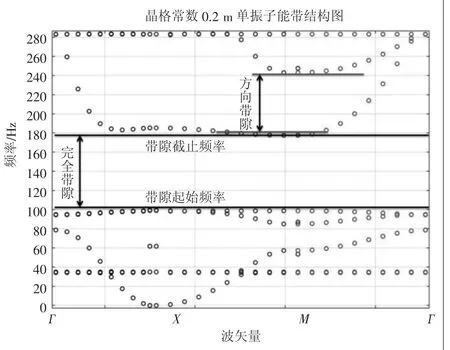
图3 二维声子结构能带结构图
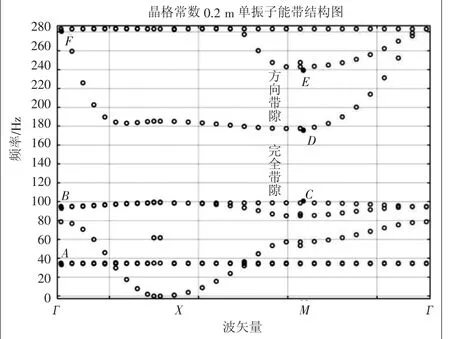
图4 能带结构图的高对称点
在能带结构图中的高对称点(A~F)进行标记,并结合原胞的振动模态逐一分析其位移振型。
分析图3,存在三条平直模式能带、一段完全带隙及一个区域的方向带隙。分析单振子位移振型图,如图5(a)~图5(f),在A点模态39 Hz附近,在局域共振子内部形成一个旋转模态,振子中心形成一个绕z轴呈涡轮状的体位移,由于共振子未能与基体板件中的能量波进行耦合作用,色散能带上所有的能量均能在板内进行自由传播从而形成通带。在B、C点99 Hz附近,共振子和基板内的lamb波相互作用,使纵向平面内平移模态产生的水平剪切波和面外横向模态产生的弯曲波相互作用形成一个剪切模态抑制z方向的扭转模态振动,致使质量块(B)沿垂直方向产生剪切形变,产生z方向的垂向力分量给基体板,同样此时的软体层(A)橡胶阻尼起刚度弹簧的作用产生谐振从而打开禁带形成带隙的下边界。在D点180 Hz频率处,质量体(B)沿垂直方向施加给基板产生一个垂向力抑制局域声子板中的弯曲波横向弯曲振动,引起共振子和基体板件之间反相振动,此时产生的垂向力致软体层橡胶阻尼等效为受压的弹簧装置,产生形变消耗弯曲波的内部能量,截断带隙形成上边界,故在99~180 Hz范围内形成完全带隙,绝对带宽为81 Hz,如图3在此频率范围内存在完全带隙。而在180~240 Hz之间大部分区域未出现本征频率,称之为方向带隙,同样在E点的产生一个z方向的垂向力,也能对面外模态的弯曲波进行抑制。

图5 高对称点的振型图
3 带边形局域共振带隙优化研究
3.1 尺寸因素对单振子带隙的影响
3.1.1 晶格尺寸(a)对单振子带隙的影响
设置步长为0.025 m的晶格尺寸0.150、0.175、0.200、0.225 m进行分析,改变其结构参数,基体板厚度发生相应变化,但总质量维持不变,如表2所示。

表2 试件模型参数
分析图6,根据带隙形成原理分析,带隙下边界起始频率和共振子的固有频率相近,由于基体板和共振子的质量不变,故下边界起始频率维持不变。当基体板的晶格常数(a)变大时,共振子在基体板的接触面填充率变小,上边界的终止频率从200 Hz向140 Hz低频方向移动且随边长的增长而逐渐减小,禁带绝对宽度变窄。
图6 F-1600型三缸单作用泥浆泵流量曲线

图6 晶格常数(a)改变对带隙影响
3.1.2 质量块B半径(r1)对单振子带隙的影响
为探究质量块B半径(r1)对其第一带隙的影响,选取步长0.01 m,r1半径分别设置为0.04、0.05、0.06、0.07 m尺寸,局域共振子的总质量恒定,其厚度发生改变,其结构参数如表3所示。
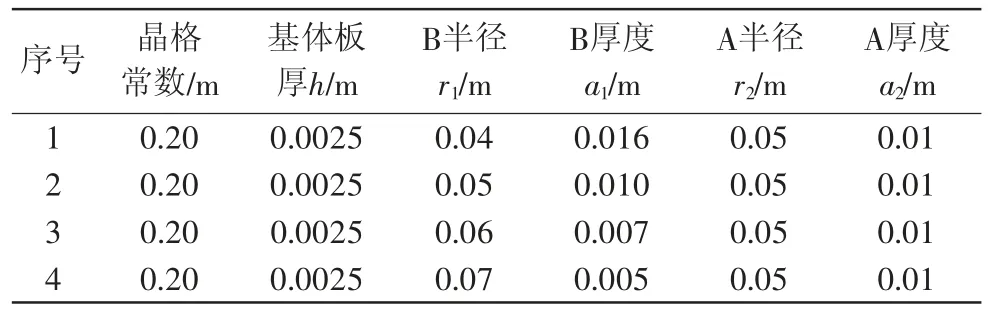
表3 试件模型参数
由图7知,当质量块B半径r1从0.05 m减至0.04 m时,带隙下边界往低频方向移动至90 Hz处,此时禁带上边界为155 Hz,完全带宽缩至65 Hz。当散射体B半径r1从0.05 m增至0.07 m时,起始频率从100 Hz往低频拓展至72 Hz,而带隙截止频率保持不变,完全带隙宽度达到了102 Hz,在软体层半径和厚度不变的情形下,散色体质量块B的半径增大对生成带隙的下边界有很好的拓宽。散射体B的半径在0.04~0.07 m的范围内,带隙起始频率先往高频移动,然后往低频拓宽,带隙宽度逐渐增大。其中0.05~0.07 m半径下截止频率保持不变。
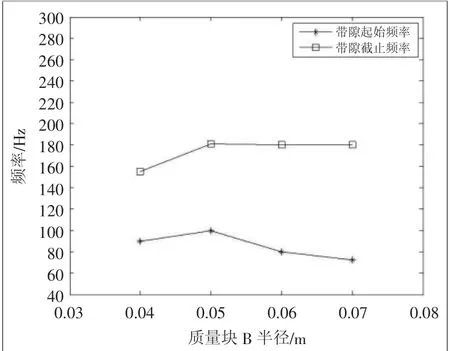
图7 质量块B半径改变对带隙影响
3.1.3 软体层A半径(r2)对单振子带隙的影响
为探究软体层A半径(r2)对其第一带隙的影响,选取步长0.01 m,r2半径分别设置为0.04、0.05、0.06、0.07 m尺寸,其总质量维持不变,而对应的厚度发生改变,结构参数如表4所示。
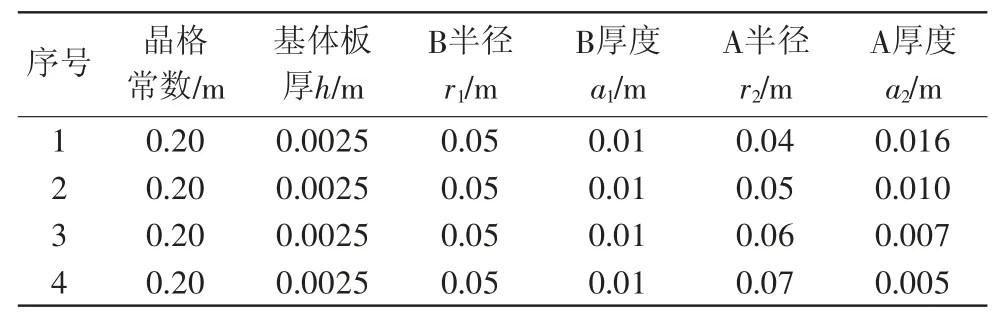
表4 试件模型参数
如图8所示,软体层A半径为0.04 m时其起始频率为48 Hz,截止频率为102 Hz。随着r2的增大,起始频率从95 Hz单调上升增至175 Hz,截止频率从182 Hz升至248 Hz。r2从0.04 m增至0.05 m时,其带隙宽度拓宽增幅较0.06、0.07 m要大。从r2增大时,其在基体板水平方向往四周进行了扩宽,相当于对“弹簧”进行并联处理。减小厚度相当于缩小对“弹簧”的串联,致使共振子等效刚度增大。根据带边型共振带隙形成机理,刚度降低使带隙下边界向高频延伸,共振子与基体板之间的振动耦合作用增强,绝对带隙宽度呈拓宽的趋势。

图8 软体层A半径改变对带隙影响
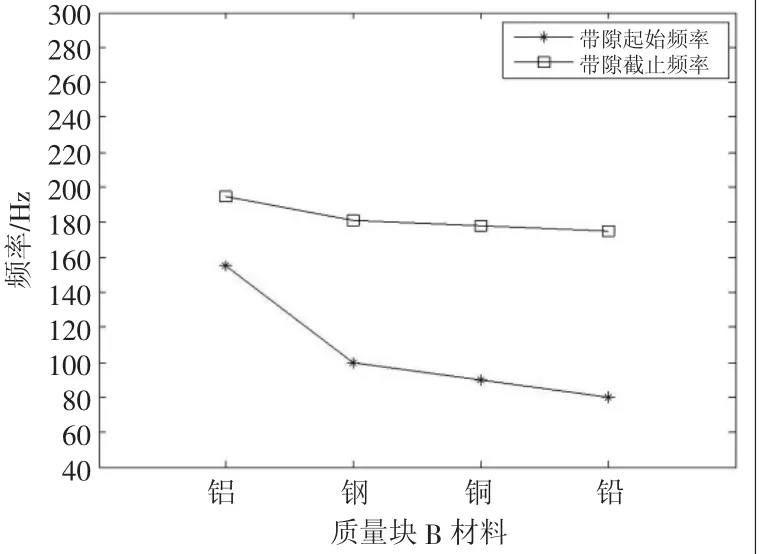
图8 软体层A半径改变对带隙影响
3.2 材料因素对带隙的影响
3.2.1 软体层A弹性模量对单振子带隙的影响
为探究软体层A弹性模量对其第一带隙的影响,仅改变软体层A的弹性模量分别设置为0.1E、E、5E、10E,其他结构参数不变,如表5所示。
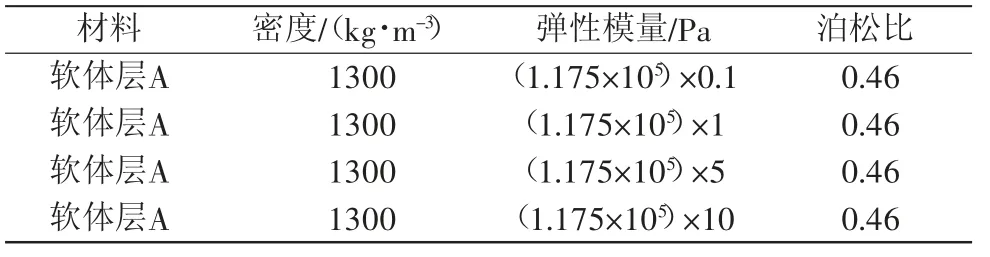
表5 软体层A弹性模量改变
如图9,设置标准弹性模量的0.1倍时(E1)时,其带隙下边界、带隙上边界分别为33、62 Hz,带隙宽度仅有29 Hz。究其原因在共振子质量不变时,等效刚度与振子的固有频率成正比关系,当弹簧等效刚度减小时相应的固有频率也降低。当弹性模量降低时,使局域共振子变“软”,其与基体板的耦合作用减弱,从而带隙的起始频率降低,带隙宽度变窄。反之当弹性模量增大5倍(E3)、10倍(E4)时,软体层A的弹性系数相应减小,共振子的等效刚度变大,共振子和基体板两者之间的耦合作用增强,带隙移至高频,带隙宽度拓宽。

图9 软体层A弹性模量改变对带隙影响
3.2.2 散射体质量块B材料密度对单振子带隙的影响
为探究散射体质量块B密度对其第一带隙的影响,根据密度的大小依次选取铝、钢(标准)、铜、铅等材料,其他结构参数不变,如表6所示。

表6 局域振子不同材料质量块B
分析图10,当质量块为铝件时,共振子的附加质量相比原试件降低,根据等效质量和固有频率之间反比的关系,带隙起始频率移向高频段。选用铅质量块时,由于质量块密度增加,在等效质量-弹簧系统中质量比增大,结构的固有频率降低,带隙的起始频率也降低,同时共振子和基体板中间的耦合作用增强,拓宽带隙宽度,但缺点是附加的质量增大。
4 结论
本文运用参数化设计在单层板上敷设局域共振子的声子晶体结构,分析其结构特性,利用有限元方法仿真得到500 Hz以下频率的的带隙分布情况。分析并优化各组成部分的结构尺寸和材料因素对带隙形成的影响。通过分析,可以将此研究结论运用于铁道车辆等载运设备的外壳或者地板结构,起到减振隔声的作用。
