刚性接触网跨距对弓网动态性能的影响分析

2021-07-15皋金龙

电气化铁道 2021年3期

皋金龙

0 引言

刚性接触网在隧道内相对柔性接触网具有一定优势，其接触线无张力，不用设置下锚装置，不会发生断线事故，零部件少，载流量大，安全可靠，维修工作量小，被广泛应用于地铁隧道内[1]。随着国内轨道交通线路运行速度的不断提高，对弓网系统的动态性能要求越来越高。跨距是刚性接触网的一项关键参数，弓网之间的良好受流质量需要选取合理的跨距，鉴于此，有必要对不同速度等级下刚性接触网跨距的选取进行研究。

目前，针对不同速度等级下刚性接触网跨距选取的研究较少，文献[2～4]建立弓网耦合模型，通过静力分析与弓网动态仿真分析仅研究了在160 km/h及以下速度等级下与某种型号受电弓相匹配的跨距方案，尚未对在不同速度等级下与不同型号受电弓相适应的刚性接触网跨距进行研究。本文建立刚性接触网与受电弓模型，采用弓网动态仿真技术，分析不同型号受电弓以不同速度通过不同跨距刚性接触网的弓网动态性能参数，得出不同速度等级下与不同型号受电弓相适应的刚性接触网跨距，为受电弓与刚性接触网系统设计提供研究基础。

1 弓网仿真模型

刚性接触网由汇流排、接触线、悬挂与定位结构等组成。汇流排通过一定的夹持力将接触线固定，两者形成一个整体，悬挂与定位结构主要包含门式结构与悬臂式结构。利用有限元法建立刚性接触网仿真模型时，可将汇流排与接触线考虑为一个整体，等效为欧拉梁单元，将门式悬挂结构与悬臂式悬挂结构等效为一个带质点的弹簧单元。因刚性接触网的汇流排截面惯性矩较大，通常刚性接触网成“之”字形布置，又因拉出值较小，一般最大为250 mm，相对于刚性接触网的锚段长度250 m，拉出值变化率很小，故建模时忽略拉出值的变化。

在建立刚性接触网锚段关节模型时，为使受电弓从一个锚段平滑过渡到另一个锚段，刚性接触网的锚段关节利用两锚段刚性接触网几何上重叠实现，重叠区域在空间上存在等高点，并将锚段末端的欧拉梁单元抬高70 mm[5]，刚性接触网等效模型如图1所示。

图1 刚性接触网等效模型

本文分析的跨距值分别为6、8与10 m，根据工程经验及文献[3]，建立3个锚段模型，其中跨距6 m的锚段内跨距分布为1.8 m + 2 m + 4 m + 6 m×39 + 4 m + 2 m + 1.8 m，跨距8 m的锚段内跨距分布为1.8 m + 2 m + 6.4 m + 8 m×27 + 7 m + 6 m + 2 m + 1.8 m，跨距10 m的锚段内跨距分布为1.8 m + 2 m + 6 m + 10 m×23 + 6 m + 2 m + 1.8 m。

受电弓由弓头、上框架、下臂杆、传动系统与底架等组成，结构复杂，在弓网动态仿真中需要将其进行简化。目前，多数学者进行弓网动态仿真分析时通常将受电弓结构等效为质量块模型、多刚体模型、刚柔耦合模型、柔体模型[6]，因本文不对受电弓结构特点进行分析，且根据文献[7]的研究，三质量块模型的仿真结果比二质量块模型更准确，故本文选取受电弓三质量块模型进行弓网动态仿真。本文基于交流供电制式的市域快速轨道交通线路，选取能够满足最高运行速度200 km/h的3种型号（DSA200、DSA250与DSA380）受电弓进行分析研究。

2 弓网动态性能分析

选取接触力标准偏差、接触力最大值与接触力最小值作为评价指标，分析不同型号受电弓以不同速度通过不同跨距时的弓网动态性能。

2.1 DSA200型受电弓

DSA200型受电弓以不同速度分别通过6、8、10 m 3种跨距的刚性接触网，得到受电弓在不同运行速度下的接触力标准偏差与接触力最值，分别如图2、图3所示。

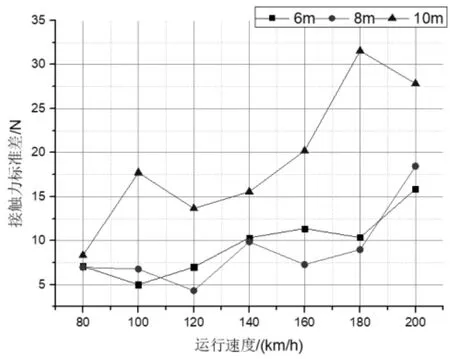
图2 弓网接触力标准偏差

图3 弓网接触力最值

选择运行速度80、120、160、200 km/h 4种工况，统计3种跨距的接触力特征值，如表1所示。

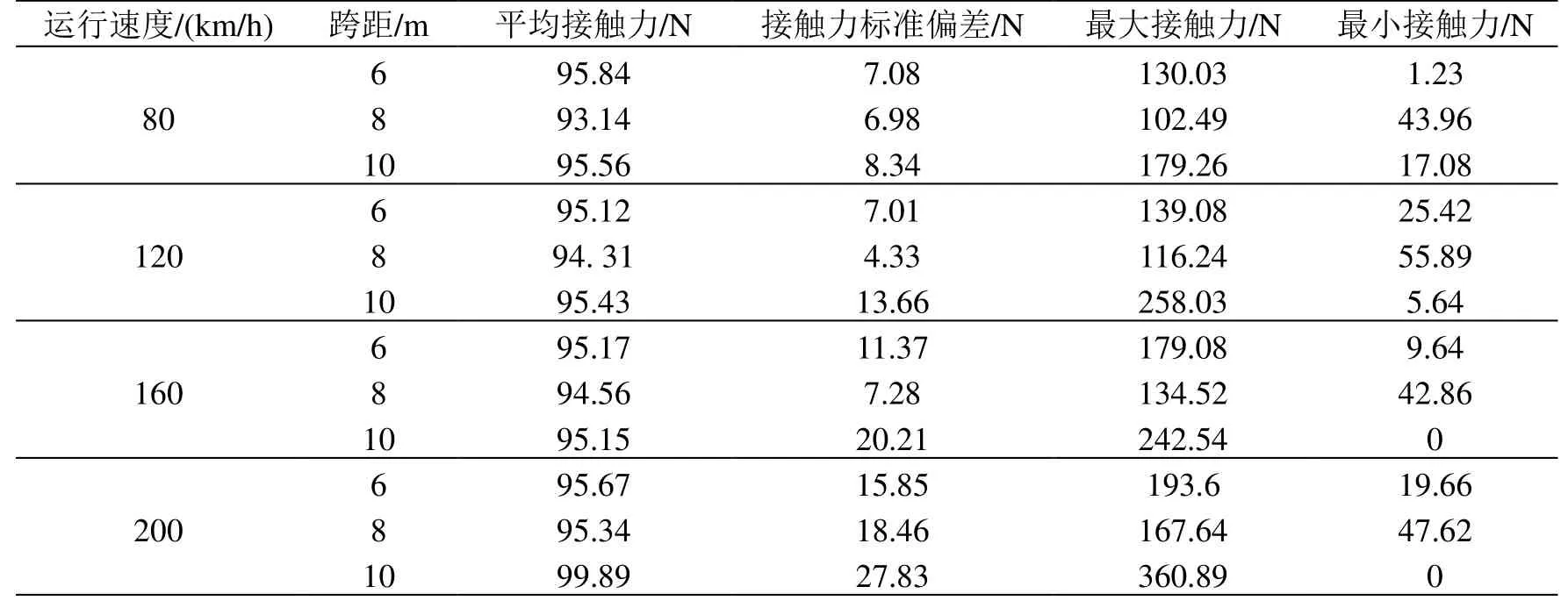
表1 DSA200型受电弓通过不同跨距接触网的弓网接触力统计

从表1可以看出，以160 km/h运行速度通过10 m跨距时，最小接触力已经为0，表明DSA200型受电弓不适合以160 km/h速度通过跨距为10 m的刚性接触网。接触力标准偏差越小，表明接触力的分布越集中于平均接触力，弓网接触质量越好。在速度为80～160 km/h时，8 m跨距的弓网接触力标准偏差最小，表明DSA200型受电弓与8 m跨距刚性接触网的适应性更好。在速度达200 km/h时，6 m跨距的弓网接触力标准偏差最小，表明DSA 200型受电弓与跨距为6m的刚性接触网匹配性较好。

2.2 DSA250型受电弓

DSA250型受电弓以不同速度分别通过6、8、10 m 3种跨距的刚性接触网，得到受电弓在不同运行速度下的接触力标准偏差与接触力最值，如图4、图5所示，弓网接触力统计如表2所示。

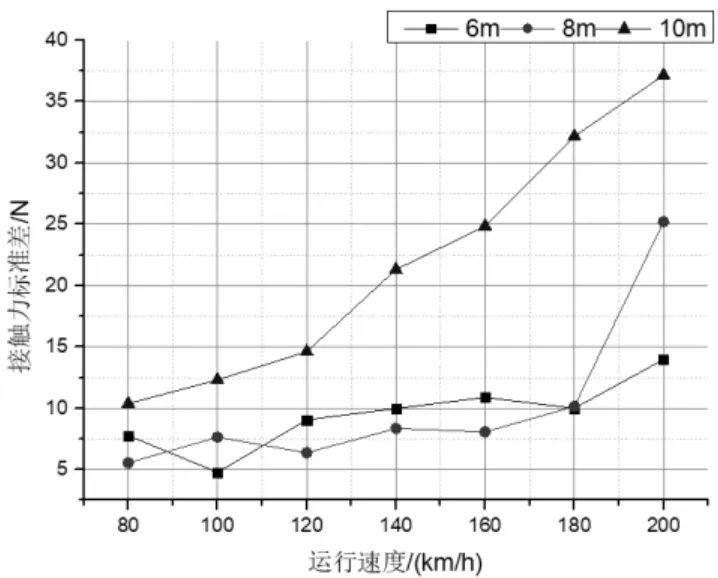
图4 弓网接触力标准偏差

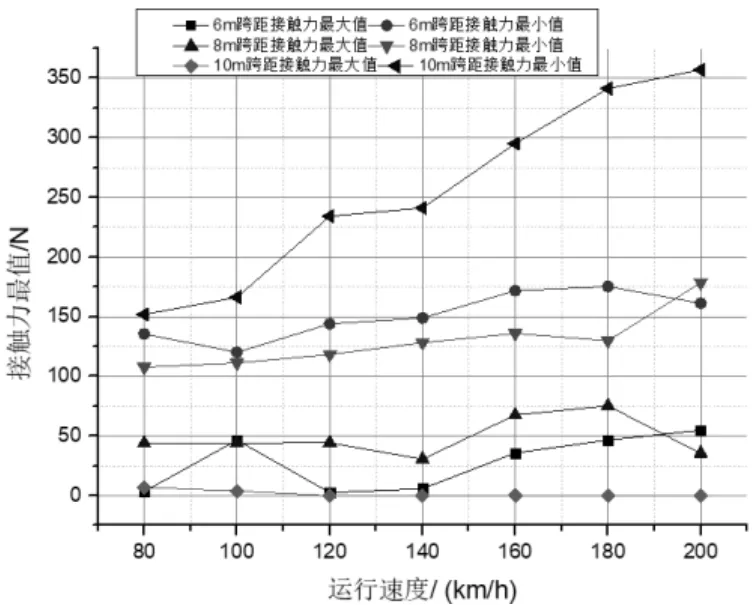
图5 弓网接触力最值

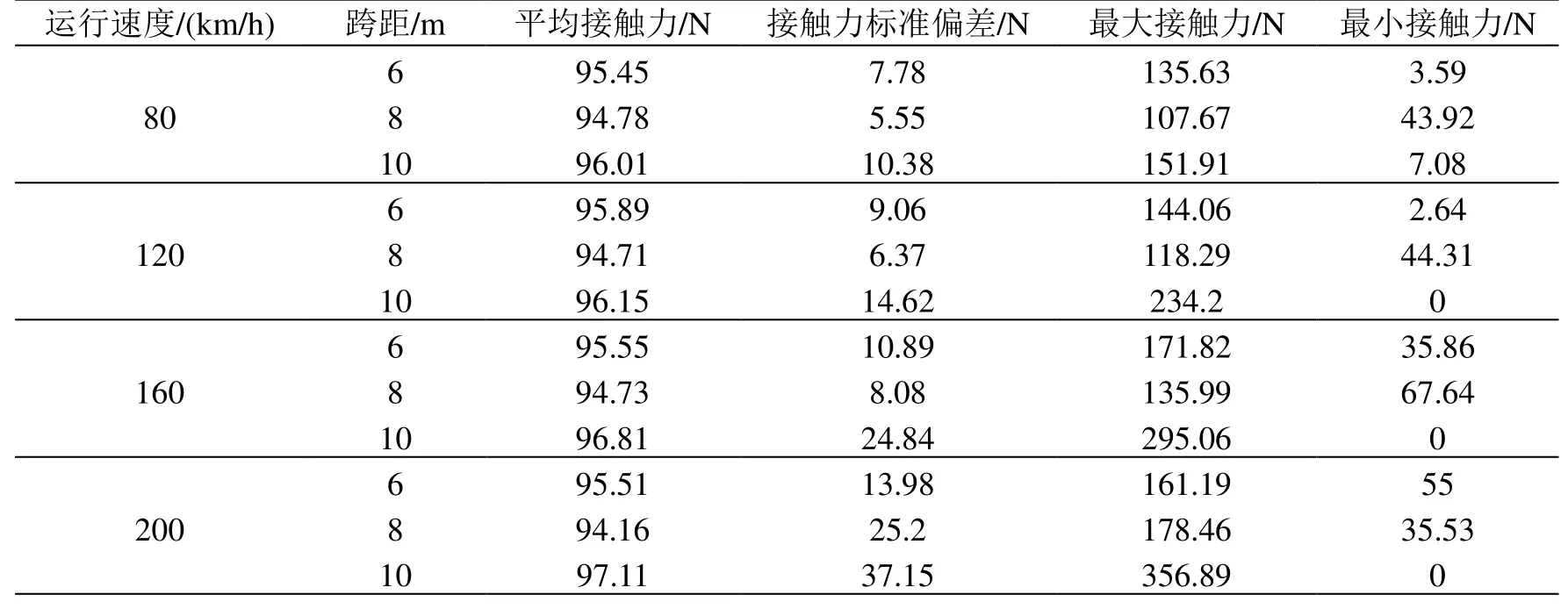
表2 DSA250型受电弓通过不同跨距的弓网接触力统计

从表2可看出，在速度达到120 km/h时，跨距为10 m的刚性接触网的最小接触力已经为0，表明DSA250型受电弓不适合以120 km/h速度通过跨距为10 m的刚性接触网。DSA250型受电弓在80、120、160 km/h速度等级下，8 m跨距的弓网接触力标准偏差最小，表明DSA250型受电弓与8 m跨距的刚性接触网更匹配。在速度达200 km/h时，6 m跨距的弓网接触力标准偏差最小，表明DSA250型受电弓与6 m跨距的刚性接触网更匹配。

2.3 DSA380型受电弓

DSA380型受电弓以不同速度分别通过6、8、10 m 3种跨距的刚性接触网，得到受电弓在不同运行速度下的接触力标准偏差与接触力最值，如图6、图7所示，弓网接触力统计如表3所示。

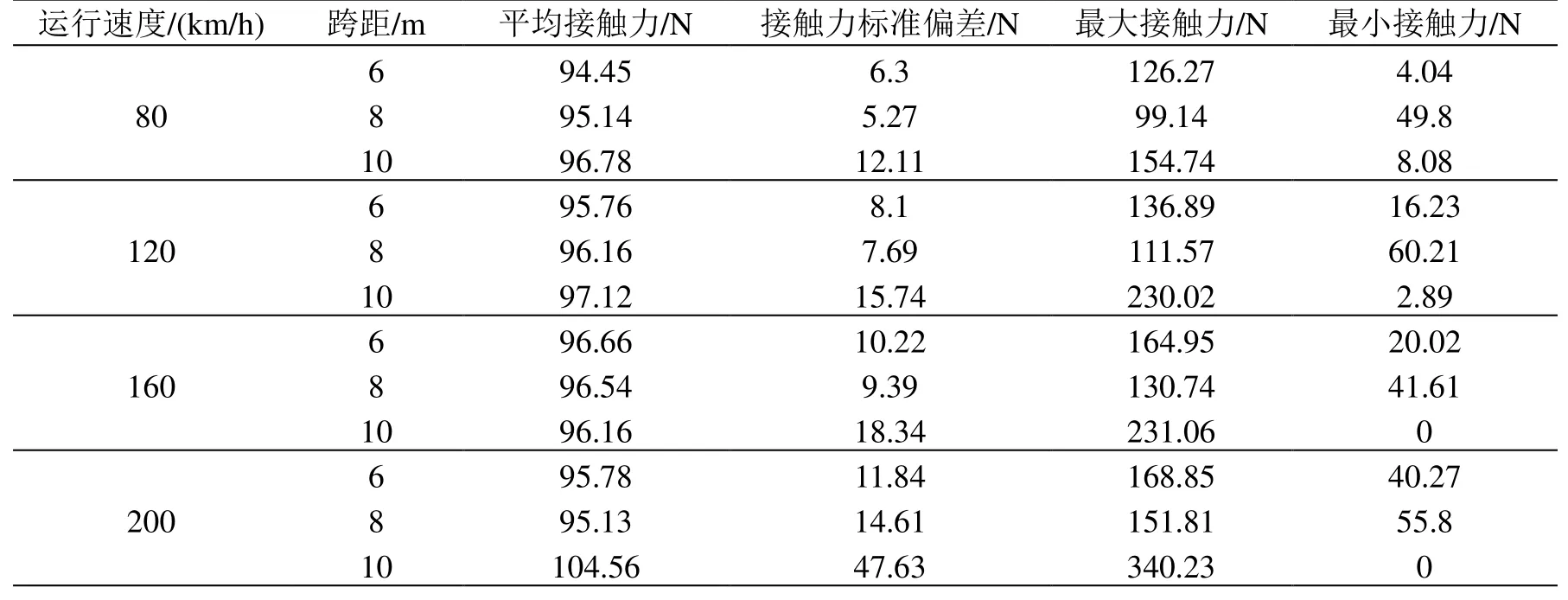
表3 DSA380型受电弓通过不同跨距的弓网接触力统计

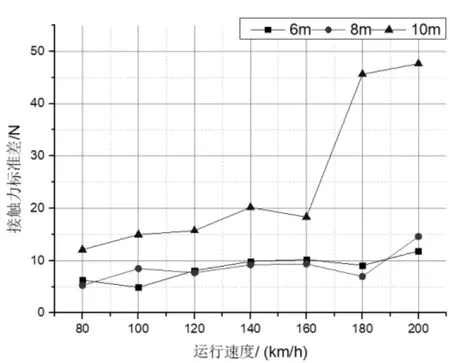
图6 弓网接触力标准偏差

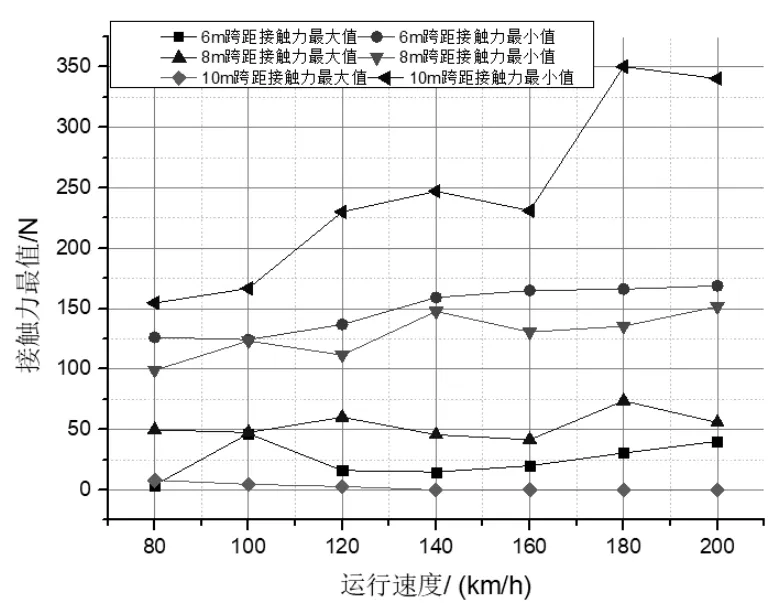
图7 弓网接触力最值

由图6可以看出，在速度为160 km/h及以上，10 m跨距的弓网接触力标准偏差呈直线增加，表明在高速运行区段，10 m跨距的刚性接触网弓网匹配关系急剧恶化。由表3可以看出，DSA380型受电弓在80、120、160 km/h运行速度下，8 m跨距的弓网接触力标准偏差最小，表明DSA380型受电弓与跨距为8 m的刚性接触网更匹配。在速度为200 km/h时，6 m跨距的弓网接触力标准偏差最小，表明此时DSA380型受电弓与跨距为6 m的刚性接触网更匹配。