旋转直驱阀的双闭环模糊PID控制仿真分析
2021-07-15邓新阳胡春艳李海涛
邓新阳, 李 伟, 胡春艳, 王 锐, 李海涛
(1. 中国科学院 工程热物理研究所, 北京 100089; 2. 中国科学院大学 工程科学学院, 北京 101400)
在传统航空发动机燃油系统中, 通常采用电液伺服阀或者步进电机驱动计量活门开度. 但电液伺服阀结构复杂, 加工困难, 同时对工作液的清洁要求较高, 而步进电机存在齿轮空回等问题, 从而限制了其在航空发动机中的应用. 旋转直驱阀(rotate direct drive valve, RDDV)没有尺寸精密的喷嘴挡板及射流管等易堵塞结构, 具有结构简单、 抗污染能力强、 可靠性高等优点, 目前已成为伺服阀的主要发展趋势[1-5]. 采用有限转角力矩电机(limited angle torque motor, LATM)直接驱动阀芯旋转, 结构简单, 便于安装和拆卸; 同时控制器通过电机直接控制阀口开度, 有利于数字化控制, 因此旋转直驱阀在各领域中广泛应用. 但RDDV系统通过电机直接驱动阀芯旋转的结构不存在限位机构, 因此对控制系统的精度和稳定性提出了较高的要求. 同时, 有限转角力矩电机在驱动计量活门旋转时, 会受液动力负载的影响, 因此系统对负载适应性也提出了较高要求.
目前, 对电机的控制通常采用经典的比例-积分-微分(PID)控制. 但随着对控制性能越来越高的要求, 传统的单闭环PID控制已经不能满足系统的快速性和准确性要求, 为提高PID控制器的性能, 已提出了很多改进方法. 如文献[6]通过比较电流环/位置环和速度环/位置环两种双闭环控制器, 提出了采用电流环+位置环的结构模式, 有效提高了系统的快速性和灵活性. 但双闭环PID控制器仍是线性控制器, 仅在工作点附近才能保持良好的控制性, 若在偏离工作点较远的非线性区域, 则难以保证系统的动态品质. 因此, 文献[7]提出了将模糊控制与PID控制相结合的方法, 解决了传统PID控制中抗扰动能力差的缺点, 提高了系统的控制能力.
本文首先建立旋转直驱阀的数学模型, 并通过MATLAB软件进行仿真分析. 在此基础上, 提出采用位置环+电流环的双闭环控制系统. 电流环采用PI控制, 在消除噪声影响的前提下, 保证系统的输出力矩快速收敛且无残差; 位置环采用PID控制, 并与模糊控制相结合, 这是因为模糊-PI控制器对高阶被控过程动态性能较差, 而模糊-PD控制器会产生较大的稳态误差. 最后通过系统仿真验证了该控制方法的快速性、 准确性及负载适应性[7].
1 RDDV系统结构及建模
1.1 RDDV系统结构
RDDV系统结构如图1所示, 直驱阀阀芯在有限转角力矩、 电机输出力矩和阀芯受到负载力矩(仅考虑负载的液动力)的共同作用下开始旋转, 角位移传感器将阀芯的实际角度反馈给控制器, 并与输入位置信号做差产生控制信号, 从而实现对系统的闭环控制.

图1 RDDV伺服系统UG三维效果Fig.1 RDDV servo system UG three-dimensional effect
1.2 有限转角力矩电机建模
力矩电机是一种单相的无刷直流电机, 在输入电流作用下, 可在一定旋转角度内产生驱动力矩, 其等效电路图如图2所示. 由图2可列出电机各环节的微分方程[8].

图2 有限转角力矩电机的等效电路图Fig.2 Equivalent circuit diagram of limited-angle torque motor
有限转角力矩电机电压平衡方程为
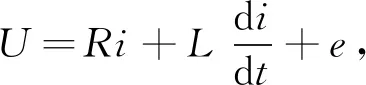
(1)
其中U为电机控制电压,R为电机电枢电阻,i为电流,L为电机电枢电感,e为电机反电动势.在不考虑电机干摩擦且为线性阶段时, 机械系统的力矩平衡方程为

(2)
其中J为转子与阀芯的转动惯量,θ为旋转角度,B为黏性阻尼系数,T为电磁转矩,Tf为负载转矩.额定励磁下电枢回路的反电动势方程为
e=Kbω,
(3)
其中Kb为电机反电动势系数,ω为电机转速.额定励磁下电磁转矩方程为
T=Kti,
(4)
其中Kt为电机电磁转矩常数.
1.3 液动力负载建模
阀芯在工作时会受到外部作用力、 惯性力、 阻尼力以及工作介质对阀芯的作用力.外部作用力即电机驱动阀芯运动的力, 惯性力和阻尼力是由于阀芯具有一定质量和运动时的阻尼作用而产生的力, 对于航空发动机转速控制器, 这两个力都很小, 在分析受力时可忽略不计[9].工作介质对阀芯的作用力包括液动力和侧向液压力, 其中侧向液压力常通过在阀芯工作表面沿圆周设置宽度较小的均压槽, 以减小其对阀芯运动的影响; 而液动力根据其性质又分为稳态液动力和瞬态液动力[10].
稳态液动力Ts是指工作介质通过节流窗口时流量不变, 由流速大小及方向变化而产生的对阀芯的作用力[11]:
Ts=2cvμAΔprcosα=Ksθ,
(5)
其中cv为工作介质流经节流窗口时的速度系数,μ为流量系数,A为节流窗口的节流面积, Δp为节流窗口前后的压力差,r为阀芯半径,α=69°为射流角,Ks为稳态液动力系数.瞬态液动力Tr是指阀芯开度变化时, 流体速度和加速度变化对阀芯产生的作用力:

(6)
其中W为面积梯度,L为阻尼长度,Kr为瞬态液动力系数.
1.4 RDDV系统建模
对式(1)和式(2)进行拉氏变换:

(7)
忽略阀芯所受的机械摩擦和Coulomb摩擦, 联立式(7)得到角位移θ(s)和输入电压U(s)的传递函数为
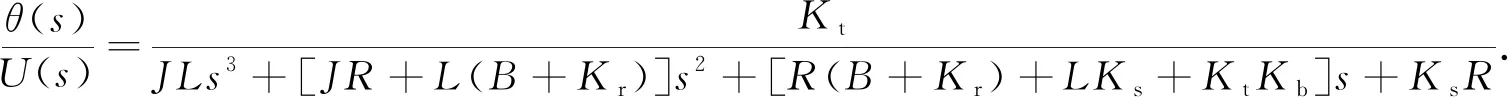
(8)
2 控制器设计
为提高系统性能, 通常采用多闭环控制方法.传统“三环”结构能有效改善系统的动态特性, 但由于闭环数多, 不能满足系统的快速性要求.因此, 考虑采用位置环+速度环或位置环+电流环的双闭环结构[12-14].由文献[6]可知, 位置环+速度环系统的负载适应性更好, 而位置环+电流环系统快速性更好.根据需求选取系统快速性更好的位置环+电流环结构.
2.1 电流环设计
电机中电流与电动机的输出力矩成正比, 电流环的作用是增强系统的抗扰动能力, 在无电流环时, 系统输出电流会随扰动的变化而发生波动, 直接影响电机的输出力矩, 进而影响电机对角度或速度的响应.同时, 在电流环中需设置限幅结构, 以防止加减速过程中产生的力矩过大.
RDDV有限转角力矩马达的绕组可视为电阻R与电感L的串联模型, 则绕组电流I(s)和驱动电压U(s)之间的传递函数[15]为
I(s)/U(s)=1/(Ls+R),
(9)
PI控制的动态方程为
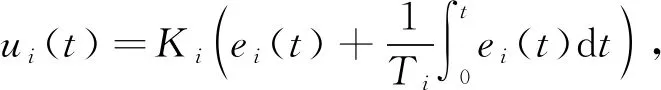
(10)
传递函数为
Gi(s)=Ki[1+1/(Tis)],
(11)
其中Ti为积分时间常数,ui(t)和ei(t)分别为控制器的输出、 输入信号,Ki为控制器比例系数.
考虑到电机需滤除电枢电流中所有的交流噪声, 因此电流负反馈需带有一阶低通滤波, 其表达式为a/(Tts+1), 其中Tt为滤波时间常数,a为电流环反馈系数. 从而可得如图3所示电流环的Simulink建模结构.
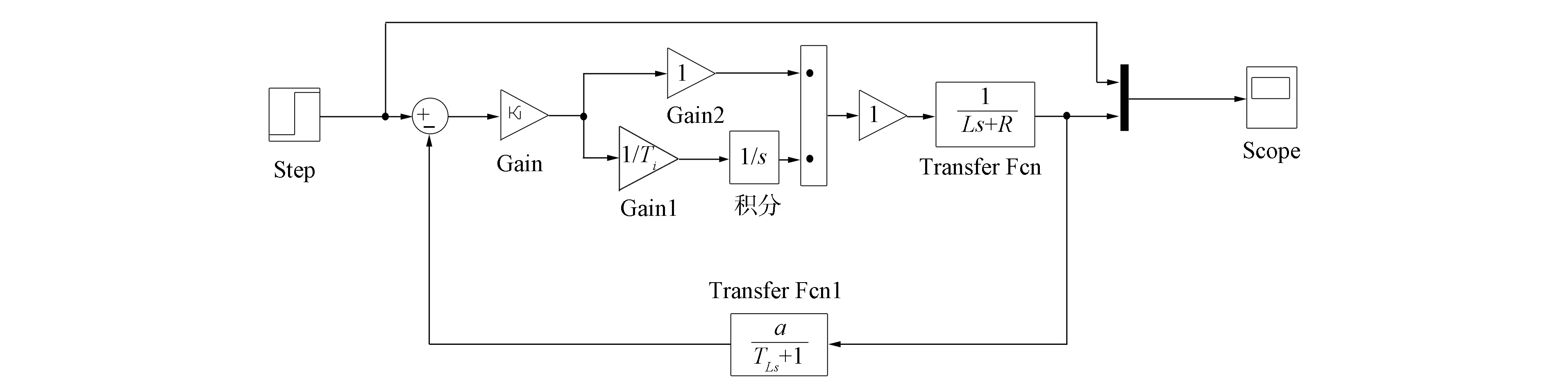
图3 电流环闭环模型Fig.3 Current loop closed-loop model
电流环的开环传递函数为
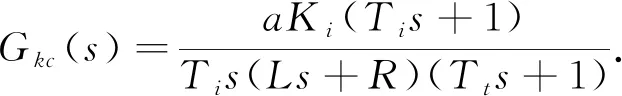
(12)
为使控制回路尽可能简单, 本文采用零极点对消的方法选取电流环的积分时间常数为
Ti=L/R.
(13)
从而开环传递函数为
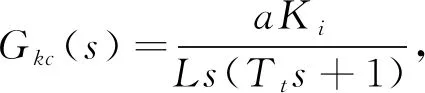
(14)
闭环传递函数为
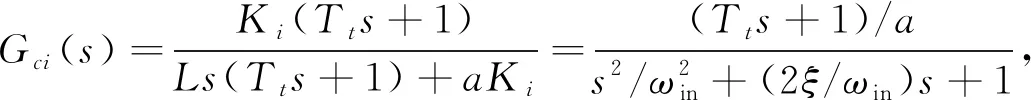
(15)

取反馈系数为a=1,Tt=0.000 1 s[15]. 选取不同的Ki值, 使得电流环的截止频率在500 Hz附近, 经过调试, 选取Ki=6. 图4为电流环闭环Bode图. 由图4可见, 系统带宽为484 Hz, 满足设计要求.
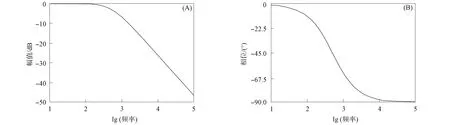
图4 电流环闭环Bode图Fig.4 Current loop closed-loop Bode diagram
2.2 位置环设计
位置环作为电机控制系统的外环, 可直接决定伺服控制系统的动态性能和静态性能指标. 因此, 位置环应采用PID控制器. PID的传递函数[14-15]为
Gpi(s)=Kp[1+1/(Tis)+Tds],
(16)
位置环的开环传递函数为

(17)
2.3 模糊控制器设计
位置环采用PID控制方法, 可使系统的动态性能和稳态性得到大幅度提升, 但当系统受到液动力负载时, PID的定常参数无法适应多变的负载, 因此采用将模糊控制与PID结合的方法, 使系统既能满足控制精度高、 响应速度快的要求, 又能保证其灵活性和较强的适应性.
以角位移误差E和误差变化率EC作为输入, 以控制参数的变化量ΔKP,ΔKI,ΔKD作为输出, 采用模糊控制方法对系统进行控制参数的实时整定. 选取7个模糊语言值, 记为{NB,NM,NS,ZO,PS,PM,PB}, 作为输入和输出的模糊状态描述, 三角函数在论域范围内灵敏度较高, 将其选作NM,NS,ZO,PS,PM等中间模糊状态的隶属度函数. 而NB和PB选用高斯形隶属函数, 以保证系统两端能平滑过渡. 图5为模糊控制器隶属函数示意图.

图5 模糊控制器隶属函数示意图Fig.5 Schematic diagram of membership function of fuzzy controller
根据文献[15-16]建立模糊控制规则, 使系统在不同的输入条件下, 输出不同的ΔKP,ΔKI,ΔKD, 从而对PID控制参数KP,KI,KD进行在线整定. PID中的控制参数为
KP=KP0+ΔKP,KI=KI0+ΔKI,KD=KD0+ΔKD,
(18)
其中KP0,KI0,KD0为控制参数的初始值.模糊控制规则表如图6所示.
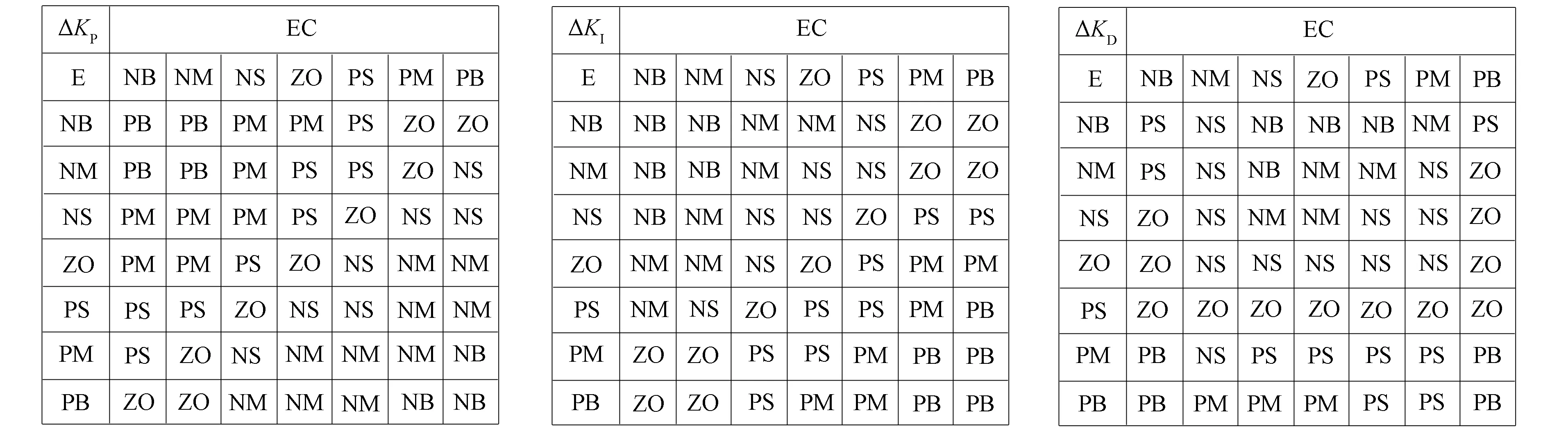
图6 ΔKP,ΔKI,ΔKD模糊控制规则表Fig.6 ΔKP,ΔKI,ΔKD fuzzy control rule tables
3 仿真校验
下面利用MATLAB/Simulink软件搭建旋转直驱阀模型, 分析其在不同控制方法下的响应.
3.1 阶跃响应
分别对传统PID、 双闭环PID和模糊双闭环PID控制器下的旋转直驱伺服系统输入一个阶跃信号, 得到响应曲线如图7所示. 由图7可见, 常规的PID控制器、 位置/电流双闭环控制器和模糊双闭环PID控制器在阶跃信号下, 响应时间分别为0.22,0.19,0.02 s, 并且常规的PID控制会出现较大的超调量. 模糊PID控制极大缩短了响应时间, 这是因为当系统的输入信号E较大时, 控制器会取较大的ΔKP和较小的ΔKI, 在保证系统快速响应的基础上, 防止出现较大的超调; 当E为中间值时, ΔKP会适量减小, 同时ΔKI和ΔKD取值适中, 以保证响应速度; 当E较小时, 为保证系统的稳定, ΔKP和ΔKI会适当增大. 因此, 常规PID控制效果不理想, 模糊双闭环控制缩短了调节时间, 改善了控制效果.
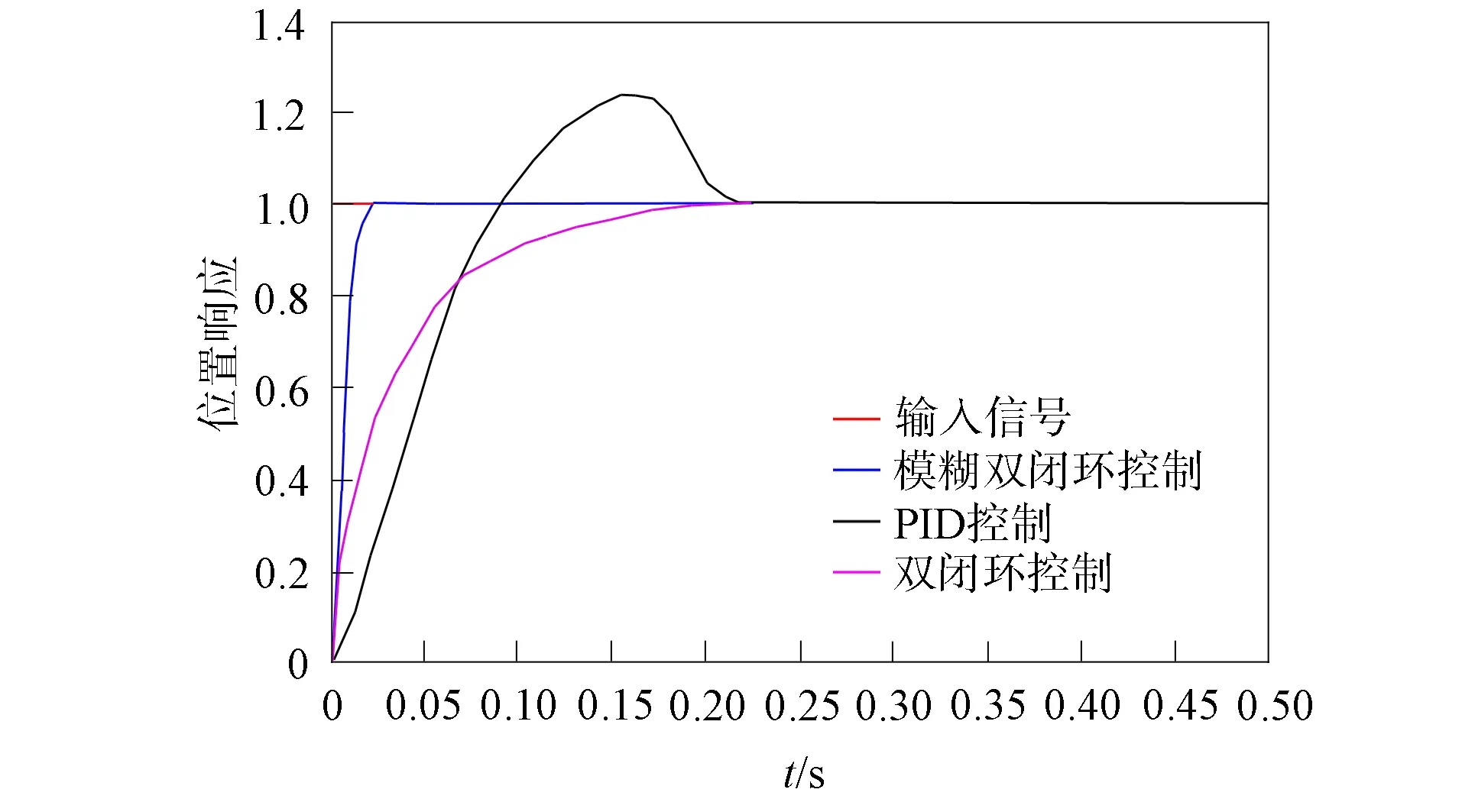
图7 不同控制器的位置阶跃响应曲线Fig.7 Position step response curves of different controllers
3.2 正弦响应
对常规PID控制和模糊PID控制输入不同频率的正弦波信号, 响应结果如图8和图9所示. 由图8和图9可见: 当输入信号的频率较低时, 两种控制方法均具有良好的跟踪性能; 但当系统的输入信号频率较高时, 常规PID控制方法出现明显的超调, 并且大幅度滞后, 而模糊PID控制虽然有小幅度滞后, 但响应速度明显更快, 并且无超调量, 其动态跟踪特性明显优于常规PID控制. 这是因为在参数整定过程中, 当系统输出大于给定输出时, ΔKI会取小值甚至负值以减小KI, 保证系统的稳态精度, 系统上升时间长于要求时间时, ΔKI和ΔKP同时增大, 保证了系统的快速性.
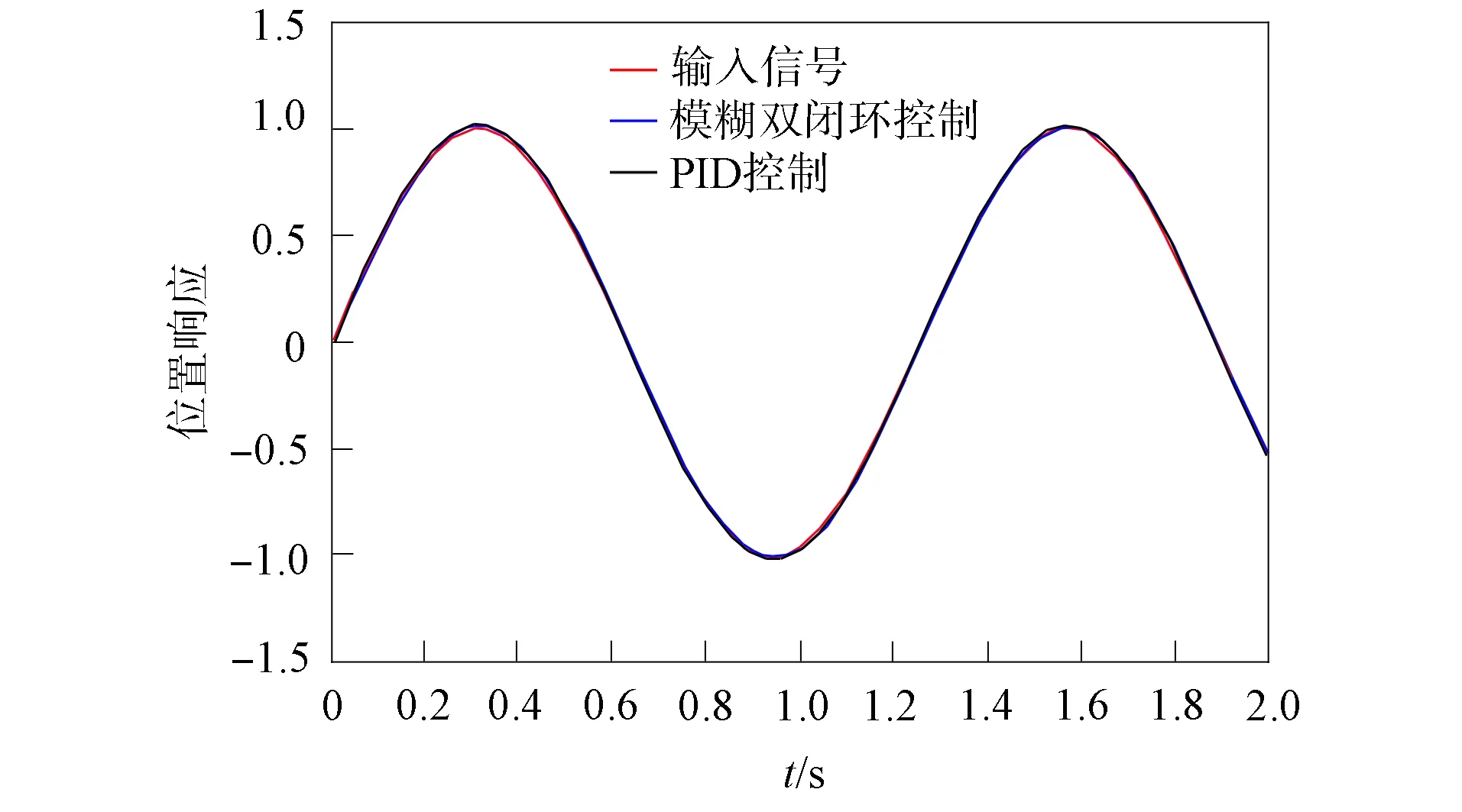
图8 输入20 rad/s时的正弦响应曲线Fig.8 Sine response curves at 20 rad/s
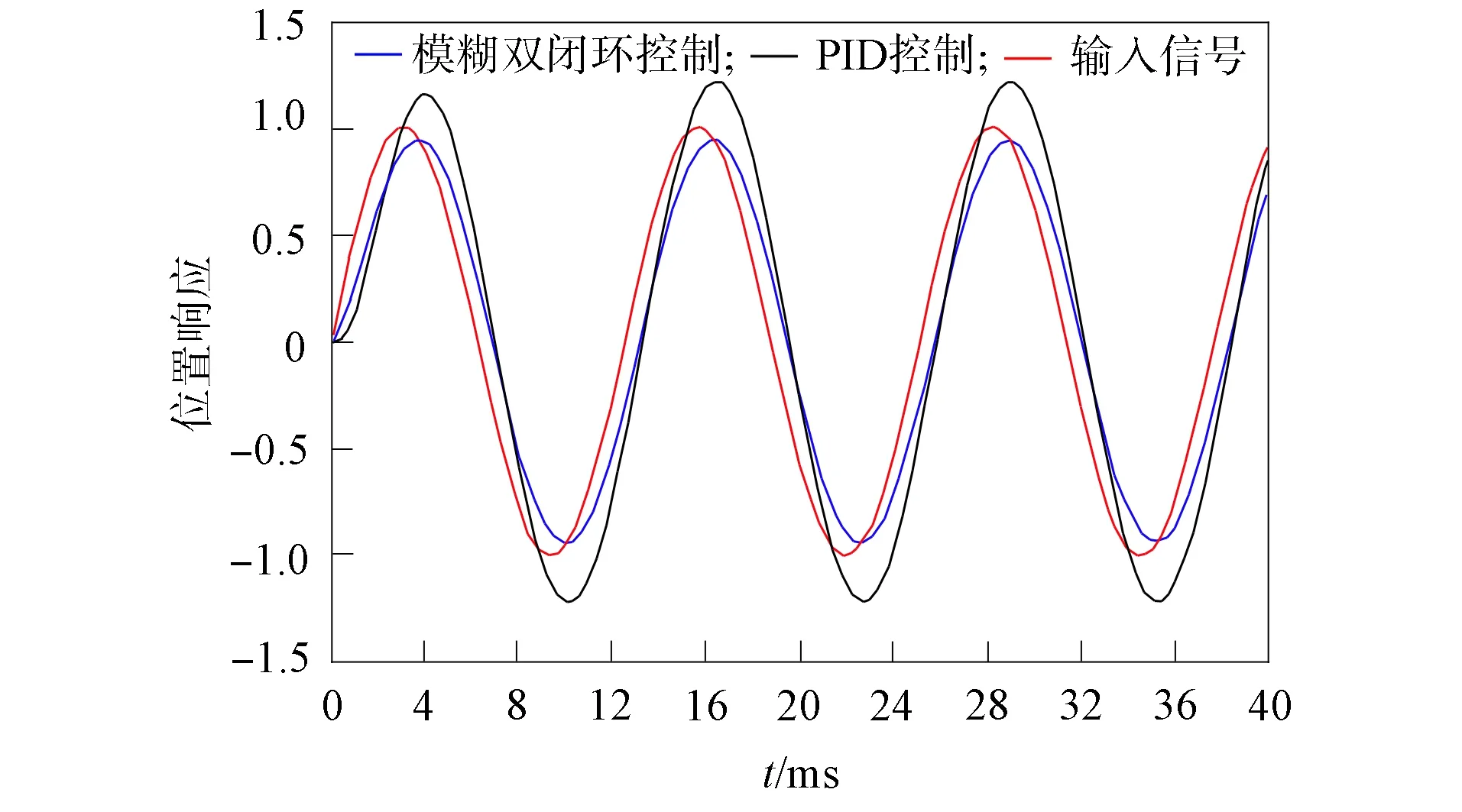
图9 输入200 rad/s时的正弦响应曲线Fig.9 Sine response curves at 200 rad/s
3.3 系统Bode图
图10为采用模糊PID控制时系统的闭环Bode图. 由图10可见, 当频率的回路增益为-3 dB时, 系统的相位裕度为48.4°, 带宽为98.3 Hz, 系统闭环稳定.
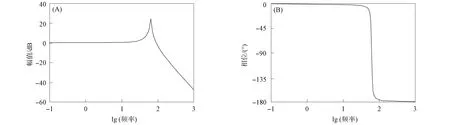
图10 系统闭环Bode图Fig.10 System closed-loop Bode diagram
综上所述, 为提高旋转直驱阀的动态特性, 本文通过MATLAB建立了RDDV系统的数学模型, 并在此基础上提出了采用位置环/电流环的双闭环控制结构, 位置环采用PID控制, 并与模糊控制相结合, 从而实现对PID控制参数的自整定. 由仿真分析可得如下结论:
1) 采用模糊PID控制方法可显著提高系统的响应速度, 缩短调节时间;
2) 通过施加负载扰动, 系统可在极短的时间内恢复到正常工作状态, 因此采用模糊PID控制可有效克服未知扰动对系统性能的影响;
3) 由输入不同频率正弦信号的仿真分析可见, 模糊PID在保证系统无超调的前提下, 相位滞后明显低于常规PID控制, 具有更好的跟踪性.
