双悬臂式压电振动给料器设计与性能分析
2021-07-15林学洋高兴军邓子龙
林学洋,高兴军,王 月,邓子龙
(1.辽宁石油化工大学机械工程学院,辽宁抚顺113001;2.沈阳隆基电磁科技股份有限公司,辽宁抚顺113122)
科技的发展使工业对无人化和自动化的要求越来越高,对工件的自动化装配、计数以及检测等方面的应用也越来越广。振动给料器按输送方式可分为直线式和螺旋式两种,按照激振源的不同可以分为机械式、电磁式以及压电式三种,其中电磁式的给料器采用电磁铁作为激振源,由于其具有送料效率高、承载能力强、通用性好等优点被广泛应用于工程中[1]。伴随着工业生产的不断进步,输送的产品向着轻、薄、小的方向发展,电磁式振动给料器的体积大、噪声高、输送精度低等缺点无法满足现代工业对产品输送的要求,迫切需要研发新型的振动给料器[2]。
压电驱动技术的逐渐成熟,使振动给料器迎来了革新。20 世纪70 年代末,日本将矩形压电振子应用于振动给料器,并成功地研制出悬臂式压电振动送料器,它具有无电磁干扰、能耗低、噪声小、物料输送精确度高等优点,使其被广泛应用于医药、精密机械等领域[3]。近年来,日本又对压电式振动给料器进行了更深入的研究,SANKI 公司研制出各种型号的悬臂梁式压电振动给料器,并在部分领域代替电磁式振动给料器[4]。韩国仁荷大学敏捷制造与系统实验室对压电振动给料器进行有限元分析和实验验证,指出改善给料器对各种物料适应性和减少输送噪声将是进一步的研究方向[5]。我国对压电振动给料器的研究起步较晚,市面上出现的压电式振动给料器大多数来源于日本,且价格昂贵。近些年,我国的研究人员也对压电给料器进行研究,并在已有给料器的基础上进行改进。吉林大学依托863 计划的支撑,对压电式给料器进行了一系列的研究,研制出直线式、横推式、惯性式以及磁力弹簧式等新型的送料器,弥补了我国在压电式给料器研究 上的不足[6⁃8]。
1 结构设计
本文设计的双悬臂梁式压电振动给料器(振动给料器,下同)的结构如图1 所示,由顶盘、Z 型主振弹簧、矩形压电振子、底座、工型传振板、橡胶底脚组成。矩形压电振子通过螺钉固定在底座上,工型传振板的一侧通过螺栓与压电振子的自由端相连,另一侧通过螺栓与顶盘和料斗连接在一起,4 个均匀分布的Z 型主振弹簧通过螺钉将其固定在底座和顶盘上,底座与减振底脚采用螺钉将其固定在一起。

图1 振动给料器结构图
振动给料器采用矩形压电振子作为激振源,在压电振子的两侧通入正弦交流电,压电振子由于逆压电效应产生弯曲变形,两个矩形压电振子自由端的位移通过工字型传振板将位移传到顶盘,使Z 型主振弹簧产生弯曲变形,工字型支撑板同时产生扭转变形。矩形压电振子受交变信号的作用,在前半个周期内压电振子的变形使顶盘降低一个高度,料盘中的物料由于惯性的作用瞬间悬停在原来的位置并与料盘产生脱离。在后半个周期内,压电振子受到相反电场的作用,产生的变形与前半个周期相反,顶盘会上升一个高度并产生与前半个周期相反的扭转,料盘对物料产生垂直方向的支撑力和沿着圆周方向的摩擦力,当压电振子持续受到交变信号的作用时,物料沿着料槽持续不断地向前输送[9]。
2 振动给料器的动力学分析
振动给料器包含垂直振动和扭转振动两种振动模式,在垂直方向上建立动力学物理模型,如图2所示[10]。图中,m1为振动给料器上端的质量,包括顶盘、料斗、物料以及连接所使用的螺栓和螺母的质量,kg;m2为底座、主振弹簧的质量,kg;k1为矩形压电振子的刚度,N/m;k0为主振弹簧板沿垂直方向的刚度,N/m;k2为矩形压电振子和Z 型主振弹簧板沿垂直方向的等效刚度,N/m;k3为橡胶底脚的等效刚度,N/m;r1为质量块m1的绝对阻尼系数;r3为质量块m2的绝对阻尼系数;F=F1sin(wt)为压电振子变形产生的力,其中w为频率;x1和x2分别为质量块m1、m2离开平衡位置的位移,m。
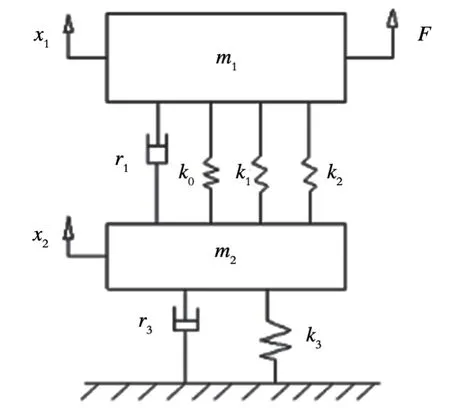
图2 振动给料器动力学物理模型
根据牛顿第一定律得出该系统的受迫振动方程:
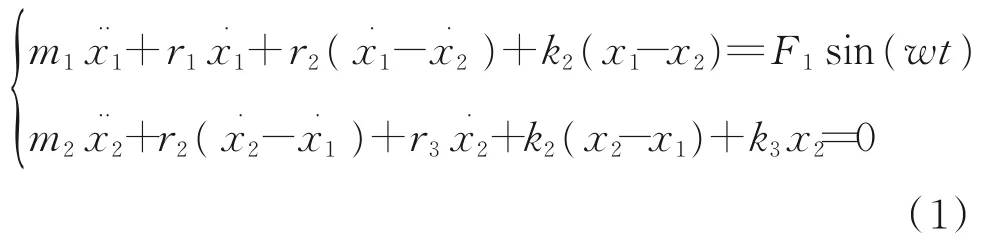
式中,r2为质量块m1对质量块m2的相对阻尼系数,k2=2k1+k0。
忽略阻尼对系统产生的影响,则方程中r1、r2、r3均为0,方程(1)可以简化为:
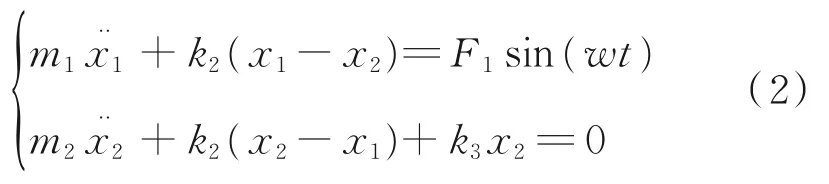
假设系统稳定阶段做等幅振动,系统按与激振力相同的频率做受迫振动。设其特解为:

简化整理可得:
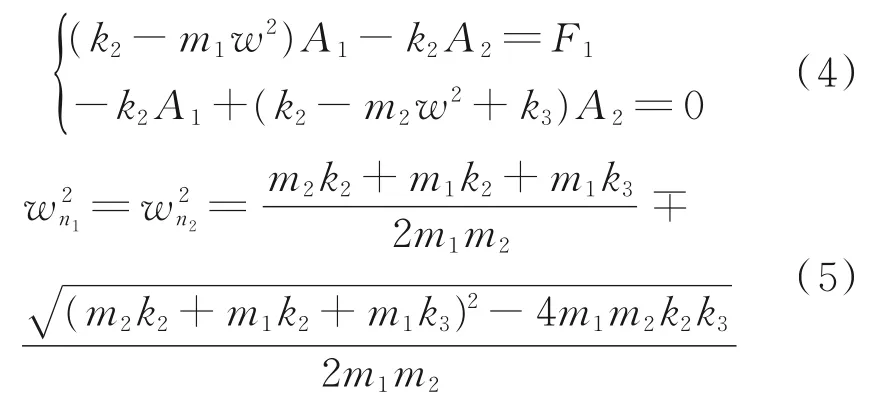
橡胶底脚只起减振和支撑的作用,k1和k2远远大于k3,所以k3≈0,则:
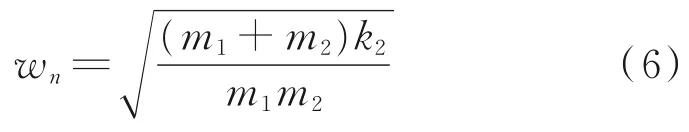
由式(6)可知,整个振动系统固有频率主要受压电振子和主振弹簧刚度以及底座、顶盘、料斗质量的影响,而减振底脚以及系统阻尼对系统的固有频率影响较小,故将次要因素忽略,忽略阻尼和减振底脚对固有频率的影响,因此实际的固有频率比计算值小。
m1和m2的振幅表示为:
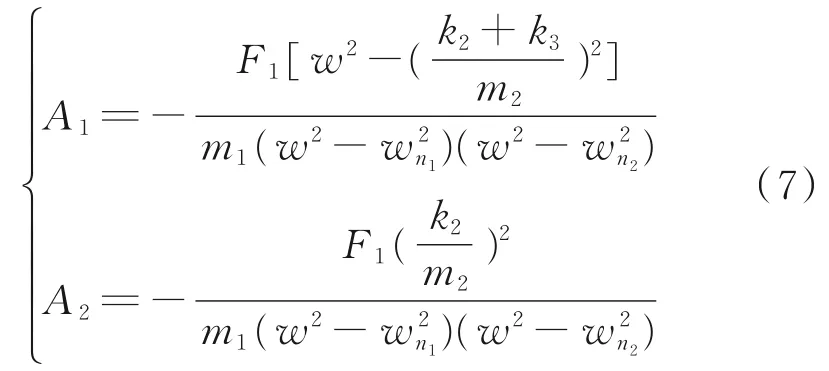
假设橡胶底脚的刚度k3=0,则m1和m2的振幅A1和A2表示为:
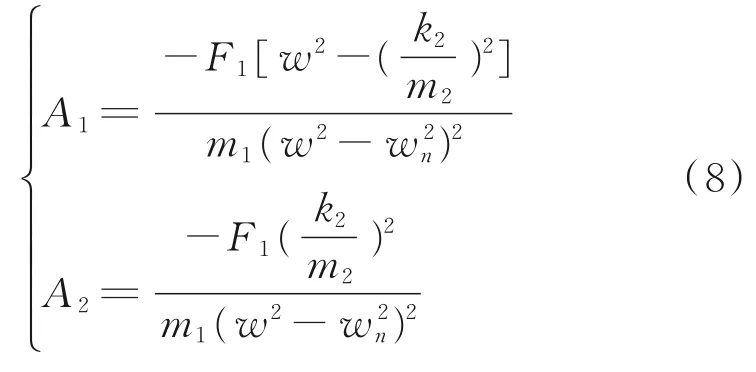
A1和A2的表达式中质量块m1和m2的振幅均与m1的质量成反比。为了保证能够快速、高效地输送物料,需要在共振的状态下振幅A1尽可能大,因此需要m2足够大,且在满足良好振动要求的基础上,适当减小主振弹簧的刚度,使顶盘具有更大的振幅,装置具备更好的性能。但是,如果主振弹簧的刚度过小,则整个装置的固有频率过小,物料将无法正常运输。
3 压电双晶片模态分析
对矩形压电振子进行振型分析时,利用ANSYS Workbench 软件进行模态分析,将矩形压电振子与底座连接的一端固定,使振子处于悬臂梁状态[11⁃13]。压电陶瓷片和基板均采用六面体单元格进行网格划分,节点数为325 783,单元格数为66 240,对压电双晶片振子进行模态分析得到前3 种振动模态,如图3 所示。由图3 可知,压电双晶片振子只有在1 阶振动模态下保持简单的弯曲变形,2 阶和3 阶振动模态包含了复杂的弯曲和扭转变形。其中,1 阶振动模态下自由端位移最大,也更符合装置共振状态下压电振子的变形情况,此时矩形压电振子的固有频率为886.14 Hz。

图3 前3 阶压电双晶片振子模态图
4 振动给料器模态分析
模态分析是对振动特性分析最有效的方法,得出的固有频率也是谐响应分析和瞬态动力学分析的前提条件。利用ANSYS Workbench 软件先对装置进行模态分析,装置由多个零部件进行装配而成,底座采用铸铁材料,主振弹簧和支撑板采用65Mn 弹簧钢,顶盘采用硬质铝合金,料斗采用不锈钢材料,材料属性见表1[14]。
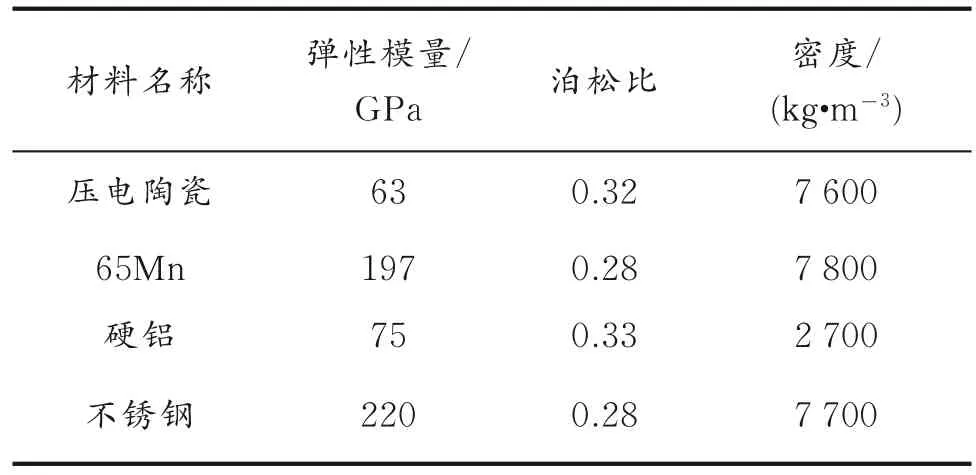
表1 材料属性
将减振底脚进行固定,压电陶瓷和基板采用六面体单元进行网格划分,其余构件则利用软件自主生成网格,节点数为331 588,单元格数为100 248,前 3 阶固有频率分别为 118.85、254.73、322.52 Hz。装置前3 阶振动模态如图4 所示。图中,红色部分表示振幅最大的位置。
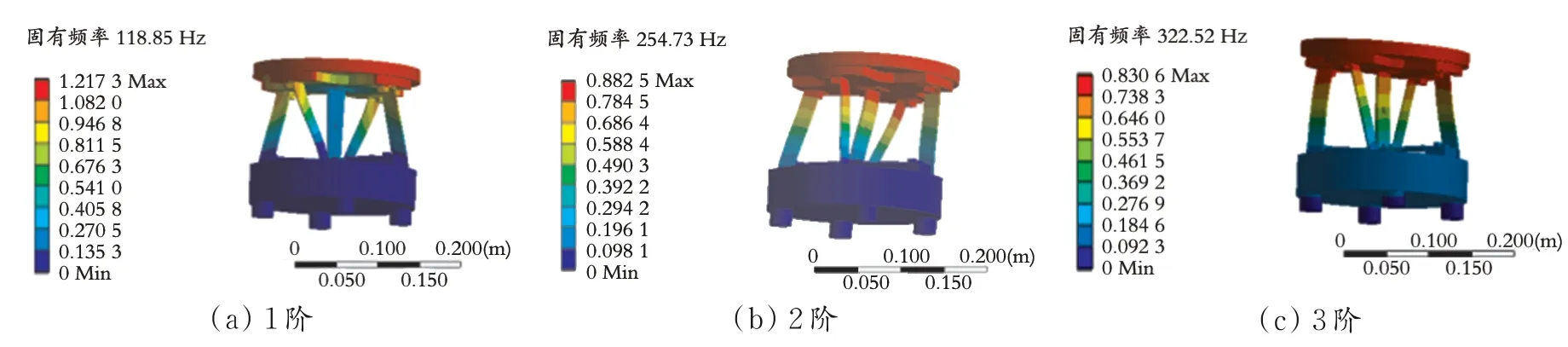
图4 装置前3 阶振动模态
由图4 可知,1 阶振型中装置的振动包含垂直方向的振动和扭转振动,结合装置的实际工作状态可知,1 阶振型更符合实际的工作情况,其固有频率为118.85 Hz,因此当装置达到共振状态时,压电振子不会发生共振。
5 振动给料器谐响应分析
垂直方向的振幅是判断振动给料器性能好坏的依据,也是装置是否能完成物料定向运输的依据,需要在压电振子的两面施加交流电,探究交流电的幅值和频率对装置垂直方向上振幅的影响。利用ANSYS Workbench 软件对装置进行谐响应分析,压电陶瓷PZT4 的介电常数矩阵[ε]、压电常数矩阵[e]和压电弹性系数矩阵[c]为:

利用full 完全法进行谐响应求解,模态分析中理论固有频率为118.85 Hz,在压电双晶片两侧施加200 V 交流电,在固有频率附近取点进行扫频求解,扫频间隔为 1.00 Hz,系统等效阻尼比ς取 0.005,对料盘垂直方向振幅进行仿真求解,结果如图5 所示。由图5 可知,当输入交流电频率为119.00 Hz 时,垂直方向的振幅达到最大值55 μm,在固有频率附近增加或减小输入频率都会使振幅降低,导致装置对物料的输送能力下降。激振频率离固有频率越近,振幅增长越明显,在偏离共振点处,阻尼比对振幅的影响较小,忽略阻尼比对装置的影响。当垂直方向振幅大于10 μm 时,物料开始沿着料槽进行滑动运输,装置的工作频率为116.00~122.00 Hz[15]。
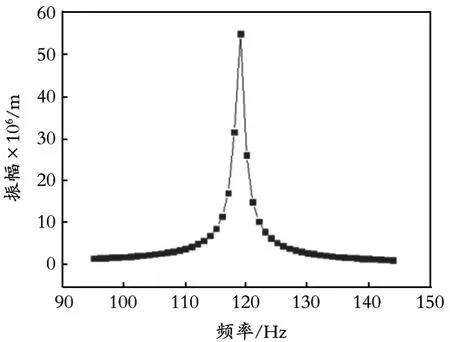
图5 料盘边缘频幅曲线
6 等效阻尼比在谐振区域的影响
振动给料器在运输物料时需要将交流电的频率采用调频控制器调节至共振状态,使垂直方向上能够输出最大位移。在共振状态下,阻尼比对给料器振幅的影响较大,为了探究阻尼比对装置工作区间的影响以及共振点处振幅的影响,利用ANSYS Workbench 软件对装置进行谐响应分析。设置阻尼比ς分别为 0、0.001、0.003、0.005,压电振子两侧的电压为200 V,频率间隔为0.20 Hz,扫频为114.00~124.00 Hz,输出垂直方向上的振幅,将仿真得出的数据在Origin 中绘制曲线,结果如图6 所示。
由图6 可知,在共振点附近,阻尼比对料盘振幅的影响较大,阻尼比对装置的影响不可忽略。但是,在确定工作频率区间时,阻尼比对装置的影响较小,频率为115.60~122.00 Hz 时垂直方向的振幅均大于10 μm,且激振频率在115.60 Hz 和122.00 Hz 时,阻尼比对系统的影响较小,可以忽略不计,最终确定装置的工作频率为115.60~122.00 Hz。
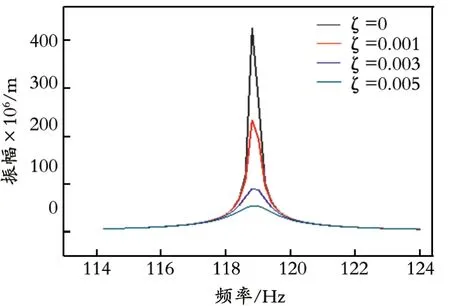
图6 装置在不同阻尼比下的幅频特性曲线
7 结 论
利用矩形压电振子作为驱动元件,采用垂直驱动的方式设计了一款振动给料装置。该装置结构简单,适用于轻小物料、精密物件的输送。其中,主振弹簧采用Z 型结构便于调整安装角度,适用于不同质量物料的输送。
对该结构送料系统进行动力学分析和物料受力分析,确定了系统的固有频率、振动幅度等决定系统性能的关键参数。
对振动给料器模型进行仿真。在装置的固有频率为188.85 Hz 的条件下进行谐响应分析时,在共振点处系统阻尼比对振幅影响较大,但偏离共振点时影响较小。忽略阻尼比对装置的影响,扫频间隔为1.00 Hz,在119.00 Hz 处振幅达到最大,其工作频率为116.00~122.00 Hz。
