采用多特征共生矩阵的模板匹配

江苏蓬，向 伟，刘云鹏，罗海波*

（1.中国科学院 沈阳自动化研究所，辽宁 沈阳110016；2.中国科学院 机器人与智能制造创新研究院，辽宁 沈阳110169；3.中国科学院大学，北京100049；4.中国科学院 光电信息处理重点实验室，辽宁 沈阳110016；5.辽宁省图像理解与视觉计算重点实验室，辽宁 沈阳110016）

1 引 言

模板匹配是计算机视觉领域一个非常经典的问题，该技术在地图与地形匹配、生理病变检测、指纹识别等领域中都有着非常重要的应用价值［1-2］。模板匹配是通过使用特定的算法在目标图像中寻找与模板图像特征内容最为相似的区域。但在实践过程中，由于图像拍摄时间、角度、环境的不同使得目标图像中目标区域与模板图像会存在一定的差异。这些不确定因素所造成的复杂场景（如光照变化、背景变化、遮挡、刚性以及非刚性形变等）会为模板匹配技术带来极大的挑战。如何实现复杂场景下的成功匹配就成为当前模板匹配算法的研究重点之一。

相似性度量是模板匹配算法的核心，传统的模板匹配算法通常采用直接对图像中的所有像素点进行逐像素匹配计算（如：差值平方和（SSD）、绝 对 误 差 和（SAD）、归 一 化 互 相 关（NCC）等）。这类算法虽然运算过程简单，但由于其面向所有特征点施加距离计算，对目标物体没有针对性，所以对背景变化非常敏感。并且当模板图像与目标图像之间存在非刚性形变、遮挡等复杂变换时，匹配精度会大幅度下降。

此外，大多数的模板匹配算法需要在模板图像和目标图像之间建立一个特定的几何参数模型，也就是说在其假定的几何参数模型成立时，匹配效果会非常好，但当异常值存在时就容易出错。这也使得这类算法只能解决某一类场景问题，从而限制了算法的适用范围。所以在复杂场景下，使用传统的模板匹配算法通常难以匹配到正确区域。

在对最新的模板匹配算法的研究中发现，Dekel等人［3］提出了一种可在无约束环境下进行匹配的最佳点对相似性算法BBS（Best-Buddies Similarity），其核心思想是判断每一对像素点对是否互为最近邻点对，并将最近邻点对数量最多最密集的地方视为最终匹配区域。这种方法对大多数的离群点具有很强的鲁棒性，可以在一定程度上克服复杂场景变化所带来的影响［4］。此后，国内学者王刚等人用曼哈顿距离代替欧氏距离并对置信度图进行阈值筛选和滤波，进一步提高了BBS算法的匹配精度［5］。但由于查找互为最近邻点对的计算成本较大，耗时较长，Talmi等人对其进行了改进，提出了可变形差异相似性算法DDIS（Deformable Diversity Similarity）。该方法引入两个关键思想：一是采用单向近似最近邻代替双向互为最近邻的方式来减少计算量，提高算法实时性；二是考虑最近邻域的形变，复杂场景下匹配精度更高［6］。但由于DDIS在原有最近邻匹配的基础上增加了空间形变量的计算，使得该方法在模板尺寸较大的情况下需要更长的运行时间。国内学者逯睿琦等人在DDIS算法的基础上添加空间金字塔模型，并且在不同尺度下提取模板图像点的显著性区域，让其更加关注目标物体本身，从而提高算法的抗遮挡和背景变化的能力［7］。Talkor等人提出的DIWU（Deformable Image Weighted Unpopularity）算法同样选取最近邻点对作为相似性度量，不同于以上方法需要每一个滑动窗口进行最近邻匹配，该方法一次性针对整幅图像进行最近邻点对计算，并以第一个窗口的匹配分数为基础通过位置差迭代计算其余窗口得分，该方法可在不降低匹配精度的基础上实现算法加速［8］。

BBS与DDIS是以计算最近邻点对为相似性度量，通过图像块之间的相似性来解决复杂场景下的匹配问题，但这种相似性度量方法只考虑了图像的局部信息，当目标物体（前景）与背景之间对比度较低时（如目标过小、目标与背景颜色相似、背景过于杂乱），或发生大面积遮挡、剧烈非刚性形变等情况时，匹配精度会下降；当同时包含多种复杂场景时，则很难匹配到正确区域。此外，传统的模板匹配算法通常只提取一种图像特征，这样很难捕获到足够的图像信息。针对这些问题，本文提出了以共生矩阵［9-11］作为相似性度量的模板匹配方法，通过统计图像特征共生矩阵信息来收集全局信息；并采用多特征融合的方法将颜色特征、HOG特征、深度特征相结合从而实现多方位的图像特征信息提取。

综上所述，本文利用共生矩阵从多特征融合所获取的大量数据中学习图像之间的相似性，能够很好的对抗光照变化、背景杂乱、几何形变、遮挡等复杂情况。与BBS和DDIS算法相比，匹配精度等高、算法鲁棒性更强。

2 基本原理

Hseu等人在1999年首次提出了利用共生矩阵进行模板匹配的思想，但当时只考虑了灰度图像和二维平移的简单情况［9］。通过对共生滤波器的研究发现，共生矩阵可以捕获图像的纹理属性而不是像素值之间的直接差异，从而隐式地表达一定的纹理相似性［12］。通过捕获并统计全局的共生信息可以得到每一个候选窗口的共生分数，我们认为来自相同纹理属性区域的图像可以获得较好的共生分数［11］。本节中我们会对共生矩阵进行介绍，以及如何实现多特征融合下的模板匹配。

2.1 共生矩阵

定义一个共生矩阵C如公式（1）所示，C(a，b)表示在图像中，像素值p，q同时出现的总次数，并根据像素之间的空间位置关系赋予不同的权重。

其中：p，q分别表示两像素点在图像中的位置，Ip，Iq则表示该位置上的像素值，δ是根据模板图像大小而变化的自适应参数，Z代表归一化因子。方括号中为判断函数，若p位置的像素值等于a，则方括号值等于1，反之为0。

从上述公式中可以发现共生矩阵是一个对称矩阵，其对角线上的元素为其自身像素在图中出现的次数，而共生矩阵的求解实质上就是遍历图像修改权重累计求和的过程。通过共生矩阵我们可以了解到两个像素值在同一区域内共同出现的概率。但共生矩阵有一个弊病，它会突显经常出现的像素值所做的贡献却忽略那些不经常出现的像素值，而所忽略的这一部分也有可能是模板中的关键信息。所以我们借用机器学习中用于衡量两个对象之间相关性的点互信息PMI来解决这一问题。PMI的基本原理如下：

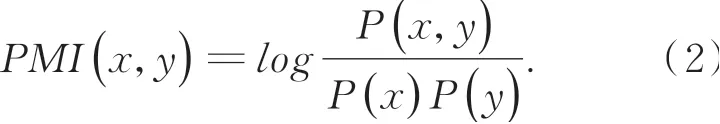
根据概率论可知：若x，y不相关，则PMI(x，y)=0；若x，y相关，则x，y相关性越大，则PMI(x，y)越大，其中的log是取自于信息论中的概率量化转换。根据这一原理，我们将共生矩阵C(a，b)除以其先验概率h(a)，h(b)以获得共生互信息矩阵。

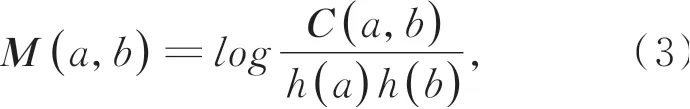
图1 共生互信息矩阵可视化Fig.1 Visualization of co-occurrence mutual information matrix

2.2 特征选取

图像的特征提取是图像处理过程中的关键一步，对后续的匹配计算有着重要的影响。本文选择了3种常用的图像特征：颜色特征、HOG特征、深度特征，它们分别表征了图像的3类不同特征属性。下文将对它们进行逐一说明。

2.2.1 颜色特征

颜色特征是一种通过像素值大小描述图像中景物表面性质的全局特征，由于其数据量小，便于查找且观感强烈，使得颜色特征成为图像处理领域最常用的图像特征。但因其对图像区域的大小、方向、空间位置等信息缺乏敏感性，所以本文选择将其与其它图像特征结合使用。

常用的颜色空间有RGB、HSV、Lab等。其中，HSV不适合在光照模型中使用，Lab颜色空间色域最大，且不依赖于光线，能有效避免颜色损失；在计算同等精度时，运行速度不逊于RBG模式。所以本文选取Lab作为算法采用的颜色空间。

2.2.2 HOG特征

梯度方向直方图（HOG）最早由Dalal等人在2005年提出，常用于行人检测，很少有人将其应用于模板匹配中，本文尝试利用其所捕获的结构轮廓信息来增强匹配的可靠性。HOG特征主要通过划分cell和block的方法来计算局部像素点之间的梯度方向与梯度强度分布。对于图像来说，梯度即为像素值变化最快的方向，由于图像的边缘与梯度是垂直关系，所以图像的局部边缘轮廓特征能被梯度的方向密度分布很好地描述。HOG作为一种对边缘形状和梯度非常敏感且能够高效捕获图像边缘信息的算子，在对图像进行检测时它能够对位置与方向空间进行量化从而削弱图像位置变化带来的影响，所以HOG特征对几何形变与光照变化都能保持良好的不变性。HOG特征的提取主要分为5个步骤：图像预处理、计算图像梯度、梯度方向统计、重叠块特征标准化、生成特征向量。图2为HOG特征提取的直观流程图。

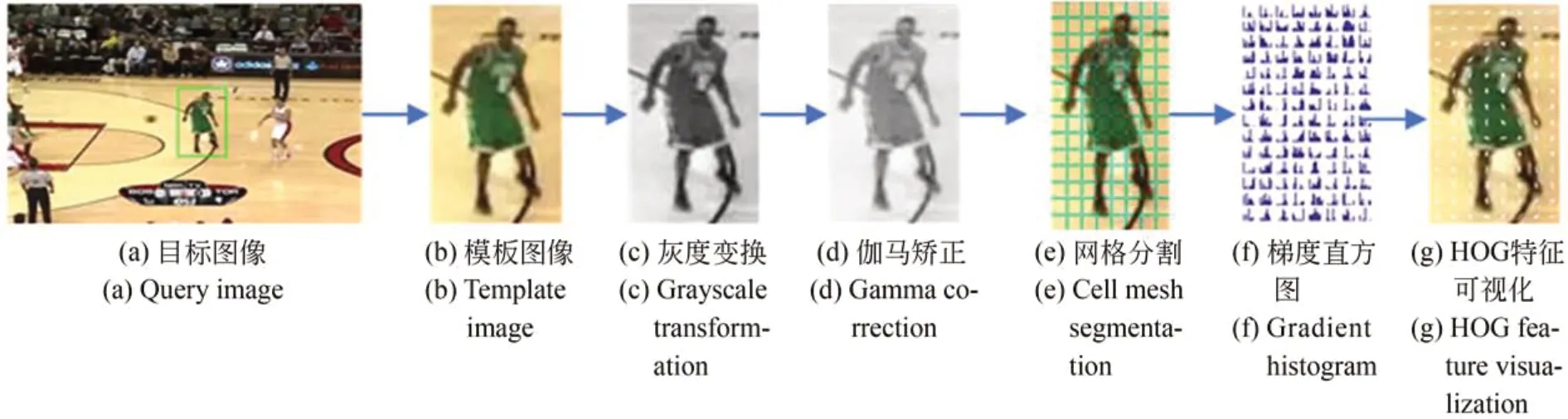
图2 HOG特征提取Fig.2 HOG feature extraction

2.2.3 深度特征

图像的颜色特征和HOG特征只是提取物体的表面特征（浅层特征），而通过深度学习的自主学习能力能够帮助我们寻找图像数据背后的规律，捕获更加本质的图像深层特征。本文利用卷积神经网络CNN来提取图像的深度特征，CNN的局部感知、池化以及参数共享特性能够有效减少参数，降低机器负载加快运行速度。本文使用当 下 流 行 的VGG19网 络 模 型［13-14］，选 取 来 自conv1_2，conv3_4和conv4_4三个卷积层输出的特征图。我们对得到的特征图进行归一化处理，之后再通过双线性插值的方法缩放到原始图像大小。

2.3 多特征融合

不同的图像特征可以表征不同的图像信息，而得到的图像信息越多对模板匹配就越有利［15］，所以我们想到通过特征融合的方法将3种图像特征进行整合，提供更加完备的图像信息，从而提高匹配算法的准确性和鲁棒性［16］。

多特征融合需要经历特征提取、特征串联、PCA降维以及k-means聚类四个步骤。首先将所提取的3种图像特征进行特征串联（本文为等比例），但是这样做会加大特征空间的维数导致后续的分类困难，同时也可能会包含一些无关或冗余的信息。为了降低特征维度减少计算的复杂度，同时减少无用信息，消除特征之间的相关性，需要对串联后的特征进行特征抽取。本文采用主成分分析法（PCA）来解决这一问题，通过用较少的主成分来表示特征以实现特征降维［17］。研究发现，当贡献率等于0.95时能够达到最好的匹配效果，在降低特征空间维度保证匹配算法实时性的同时尽量减少信息损失保证匹配精度。

如果图像匹配算法只考虑一般的256级灰度图像，那所得的共生互信息矩阵M的大小就为256×256，假设采用的是三通道的彩色图像，则的大小将变成256×256×3，这使得矩阵M将过大而无法进行应用。所以PCA降维后的特征仍无法直接用于匹配计算，还需要进行分类量化。本文采用k-means聚类［18］算法将图像特征分为k个簇类（本文中k=256），此时M矩阵的大小为k×k。

2.4 图像匹配

图3 为本文算法的流程图，经过图像预处理、多特征提取与融合后，我们将图像特征量化为k个簇类，通过求解共生矩阵C（如公式1）来统计每个簇类对在目标图像中共同出现的次数，之后通过计算共生互信息矩阵M（如公式3）来体现每个簇类对的共现概率。最后采用共生统计的方法来求解给定模板T与候选区τ⊆I的匹配概率。

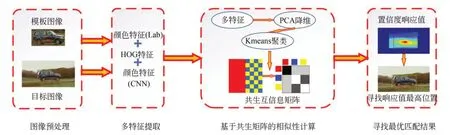
图3 算法流程图Fig.3 Algorithm flow chart

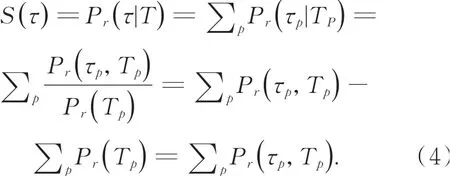
3 实验结果与讨论

本文在Dekel等人建立的公共数据集上进行了实验评估［19-20］，该数据集是从OTB数据集中选择35个标准彩色视频序列，通过恒定帧差[f，f+20]进行采样（f为随机选取），每个视频截取3对图像，总共采集105对模板图像。每一对图像的第一幅作为参考图像用于提取模板，第二幅图像作为待匹配的目标图像，所得到的图像数据集涵盖各种各样的挑战：复杂的几何形变，光照变化，尺度差异，旋转，局部遮挡等。下面从定量分析与定性分析两方面对本文的实验结果进行评估。

3.1 定量分析

我们借鉴目标跟踪中常用的准确率度量方法，将实验的检测结果与预测真值框之间的重叠率视为衡量匹配成功与否的度量标准：

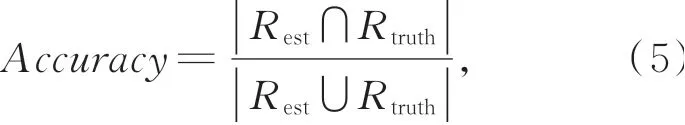
其中：|⋅|表示一个区域的像素点的个数，Rest代表实验测试结果区域，Rtruth代表人工事先标定的预测真值区域。

算法1基于多特征共生矩阵模板匹配算法Algorithm 1 Template matching algorithm based on multi-feature co-occurrence matrix

BBS算法与DDIS算法都只是单一的使用颜色或者深度特征进行图像匹配，这种方法得到的图像信息较少，使得算法在一些复杂场景下容易发生匹配失败。并且它们都没有考虑到目标的局部结构和整体轮廓特征，所以我们尝试加入HOG特征以弥补这一不足。本文通过将颜色特征、HOG特征和深度特征三者进行特征融合来获取更多的图像信息增强算法的可靠性。我们将本文算法与目前一些匹配效果较好的模板匹配算法进行了性能对比，进行比较的算法有：DDIS，BBS，SSD，NCC，SAD以及HM（颜色直方图匹配算法）。考虑到深度特征的特征空间维度较大，普通算法采用深度特征很难达到匹配实时性要求，所以在对比实验中我们只对DDIS算法分别采用了深度特征（DDIS-D）和颜色特征（DDIS-C），其余算法均使用颜色特征。通过对105组图像进行匹配实验，根据实验结果绘制了成功率曲线图并计算了曲线下面的面积（AUC）。

表1 中展示了各种算法的AUC，图4中展示各种算法的成功率曲线。通过对比计算可以发现，本文算法的AUC值为0.6586，相比于目前最好的几种模板匹配算法DDIS-D、DDIS-C、BBS分别提高了7.88%，8.14%，20.16%，并且明显优于其它传统的模板匹配算法。实验结果证明了采用特征融合的方法比简单地使用单一特征能够获得更好的匹配结果。

表1 不同模板匹配算法的AUC得分Tab.1 AUC score of different template matching algorithms

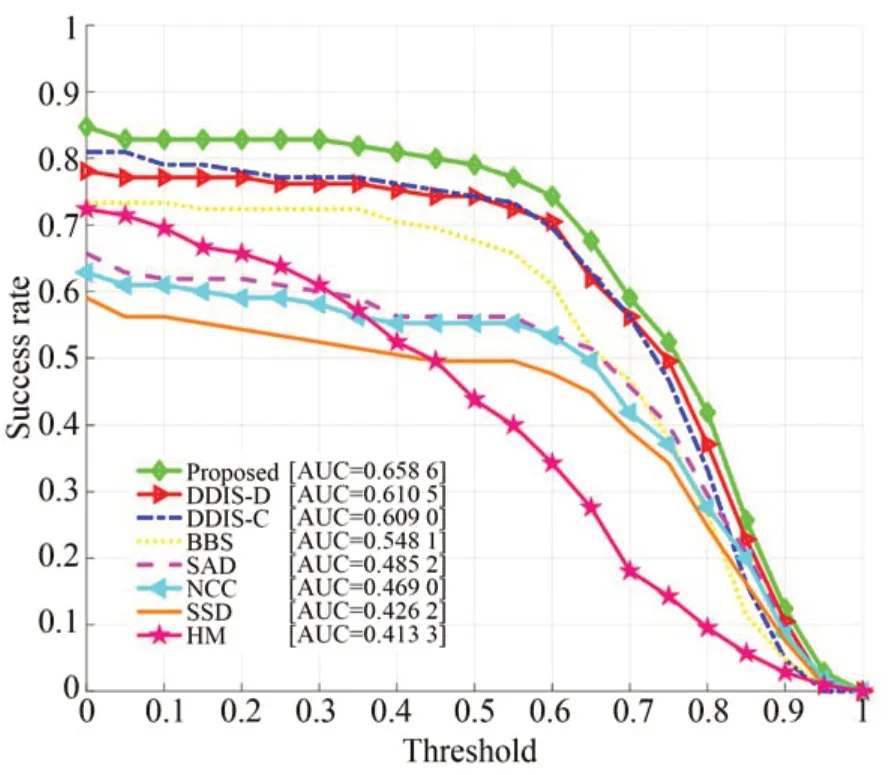
图4 不同模板匹配算法的成功率曲线Fig.4 Success rate curves of different template matching algorithms

不同于BBS算法和DDIS算法需要对最近邻进行搜索查找，本文采用通过求解共生矩阵来对图像特征进行共生信息统计，算法原理简单且易于实现。本文在电脑配置为8GB RAM、i7-7500CPU环境下分别对105组图像进行实验，对基于共生矩阵的匹配核心算法进行运行时间统计，其中匹配平均耗时为1.934 8 s，最短耗时为0.147 5 s，最长耗时为6.899 7 s。而BBS与DDIS算法的匹配耗时受模板尺寸影响下较大，当模板图像较大时，匹配耗时可达百秒以上。

3.2 定性分析

通过对比实验结果，我们选取了6组具有代表性的匹配结果（如图5），这6组图像包含了常见的一些具有挑战性的复杂场景：几何形变、近似目标区域干扰、背景杂乱、光照变化、局部遮挡、目标对象过小等；且一般为几种复杂情况同时存在。图5中的前两列分别代表模板图像和待匹配图像，后4列则表示各种算法的置信度图。从匹配结果上看（绿色为真值框、紫色框为本文算法匹配结果），DDIS算法只能成功匹配上很少一部分，BBS算法全部以失败告终，而我们的算法能够成功匹配到正确目标位置。从置信度图上对比可以发现，本文算法的置信度图是非常干净的，并且在正确位置上具有非常强烈的响应。由此可见，在这些复杂的场景下本文算法匹配成功率更高、算法的鲁棒性更强。

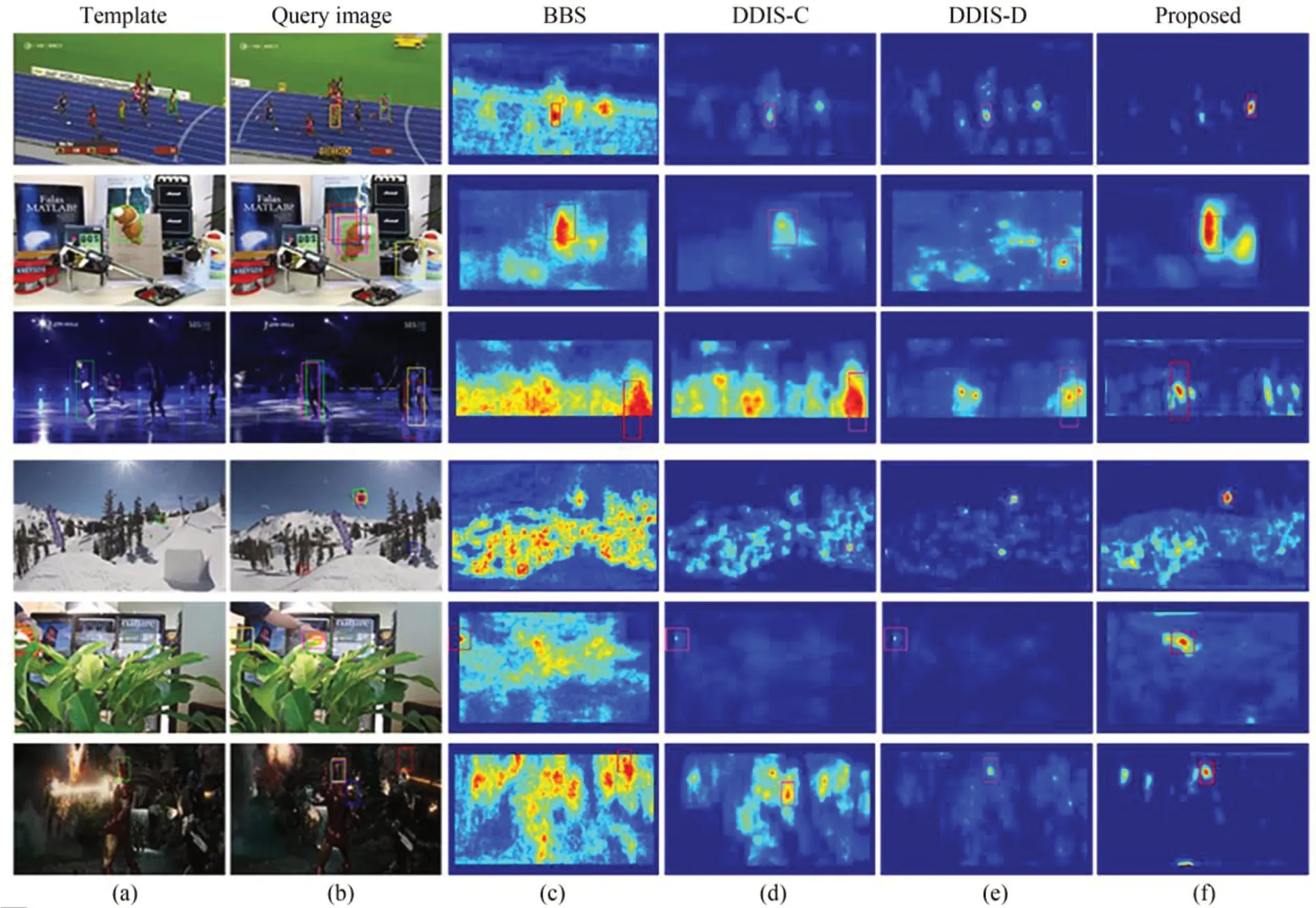
图5 不同模板匹配算法匹配结果Fig.5 Results on different template matching algorithms

4 结 论

鉴于传统的基于相似性信息统计的模板匹配算法未能充分利用各类图像特征信息，且在多种复杂情况共存的场景下算法匹配精度较低这一缺点，本文提出了一种基于共生矩阵的多特征融合模板匹配算法。提取图像的颜色特征、HOG特征与深度特征进行，并通过PCA与Kmeans算法对图像特征进行降维分类实现特征融合，从而捕获更充足的局部特征信息，再通过对共生矩阵进行信息统计的方法得到全局信息共生得分，从而将高分数区域作为模板匹配结果。本文算法的AUC得分为0.658 6，较目前较好的几种模板匹配算法都有较好提升。且该算法能够适应更为复杂的匹配场景，算法的鲁棒性更强，匹配精度更高。但是本文的算法仍然存在一定的局限性，当匹配的目标存在明显的尺度变换时，我们的方法有可能失败，这也是我们下一步努力的方向。