结构光编码测量技术在火星高分相机中的应用

曹智睿，董吉洪

（中国科学院 长春光学精密机械与物理研究所 空间三部，吉林 长春130000）

1 引 言

在首次火星探测任务高分辨率相机的研制过程中，加工了许多具有精密三维形貌要求的结构件用于高精度的标定、测试和试验等工作。为了检测这些结构件的加工精度，通常使用三坐标测量设备，以接触测量的方式获取若干采样点的空间位置信息，并进一步拟合待测表面的三维形貌。受待测表面三维形貌特点和测量效率等因素的制约，通过三坐标测量三维形貌时的采样点密度难以大幅度提高，从而制约了复杂三维形貌的测量精度；另外，通过有限采样点拟合得到的三维形貌无法有效反应待测表面局部位置的凸点、凹点等加工误差，而这些加工误差将严重影响火星高分辨率相机的标定、测试和试验精度，甚至破坏相机精密的光机结构位置关系。结构光编码测量技术具有非接触、高密度和高效率等优点，被广泛应用在工业测量、模具制造、医学影像、文物重建等领域［1-4］，可有效解决三坐标测量设备存在的上述技术问题。

结构光的编码方法是结构光编码测量技术的重要基础，随着DLP数字投影技术的发展，结构光编码的灵活性和多样性大大增加，现有的结构光编码方法主要包括格雷码［5-6］、正弦相移［7-9］、梯形相移［10-12］、三角相移［13-14］以及格雷码与相移结合［15-18］等。其中，格雷码与正弦相移结合的编码方法因其高采样密度和易于相位展开等优点应用最为广泛。传统的格雷码与正弦相移的结合方式为对称式结合，该编码方法要求正弦相移周期与格雷码最小编码周期相等，且边界对齐。在实际应用过程中，受被测物体形状、表面材质、测试环境照明和格雷码二值化阈值等因素的影响，格雷码和正弦相移周期边界产生周期错位，从而导致周期边界位置的绝对相位解算误差。为了解决这个问题，研究人员提出了多种不同的方法。第一类方法的核心思想是通过优化滤波算法、自动阈值设置方法、亚像素边界定位算法和非线性误差校正算法等方法提高格雷码和正弦相移周期边界的定位精度［19-23］，从而一定程度地减小了周期错位误差产生的范围和概率，但是此类方法并不能彻底消除周期错位误差。第二类方法的核心思想是通过相邻像素的比较来识别格雷码或正弦相移绝对相位的变异点，然后根据具体情况确定周期错位误差的校正方案［24］，此类方法复杂且具有一定的局限性。例如，当周期错位误差的范围超过一个像素时，某些位置的解码错误无法得到纠正；当被测物体表面形貌变化剧烈时，一些正常的相位突变可能被误判为周期错位误差，从而导致错误的校正。第三类方法的核心思想是通过改进编码方法从原理上消除周期错位误差。例如，Fu X和Yu X等人提出的梯形相移非对称结合格雷码的方法［25］，通过格雷码与梯形相移区域码的双重约束减小周期错位误差，但是梯形相移在采样密度和测量精度上的固有缺陷使其无法取代格雷码结合正弦相移的重要地位；Zhang Q提出了一种格雷码与正弦相移的互补编码方法［26］，通过投射额外的格雷码图像（正弦周期与附加格雷码周期相同，但边界对应关系发生偏置），获取两个互补的绝对相位值来消除周期错位误差，但是投影额外的格雷码会在一定程度上降低测量效率，难以适用于高精度动态三维测量等应用场景。

本文提出对四步正弦相移进行区域编码的概念和方法，并将具有区域编码的正弦相移与格雷码进行非对称结合，通过格雷码和区域码的双重约束，从原理上消除了格雷码结合正弦相移的周期错位现象。本文提出的方法与梯形相移非对称结合格雷码的方法相比较，具有更好的采样密度；与Zhang Q提出的互补编码方法相比较，不需要增加额外的格雷码投影数量，有利于提高投影测量效率。

2 基本原理

2.1 正弦相移区域编码与相对相位编码

在以往的应用中，正弦相移只存在相位编码，不存在区域编码。本文提出了正弦相移区域编码的概念和四步正弦相移区域编码的方法，目的是将具有区域编码的正弦相移与格雷码进行非对称结合，通过格雷码码值和正弦区域码的双重约束最大限度地减小周期边界处的解码误差。

四步正弦相移的间隔为1/4正弦周期，每个正弦相移周期均可划分为四个区域，区域编码N分别取值0，1，2，3，如图1所示。

图1 影像测量系统原理图Fig.1 Block diagram of image measuring system

四步正弦相移区域编码的规则如表1所示，表中I1~I4分别代表第1幅至第4幅正弦编码图案中特定像元位置的灰度值。

表1 四步正弦相移区域码编码规则Tab.1 Region encoding rules of the four step sinusoidal phase-shifting

四步正弦相移相对相位φ的解码方法如公式（1）所示，式中fix表示向下取整运算，例如：

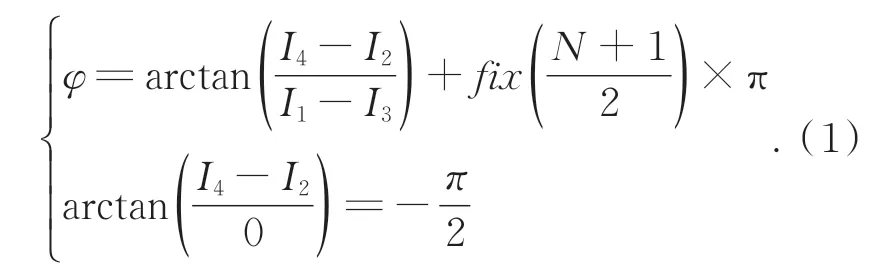
2.2 格雷码非对称结合正弦相移

格雷码非对称结合正弦相移编码方法改变了格雷码最小编码周期与正弦相移周期之间的周期对应关系和位置对应关系。在新的编码方法中，正弦相移周期大于格雷码最小编码周期，且格雷码最小编码周期边界分别位于正弦相移两个区域的中间位置。该方法的核心思想是避免格雷码码值k与正弦相移区域码码值N同时变化，即使一个编码的判读产生了误差，仍可通过另一个不变的编码抑制周期错位误差的产生。

格雷码与四步正弦相移非对称结合的具体方法如下：首先，设置正弦相移周期占据4m像元位置（数字4代表四步正弦相移所划分的4个区域），格雷码最小编码周期占据4n像元位置；为了保证格雷码最小编码周期边界分别位于正弦相移两个区域的中间位置，则m和n应满足公式（2）所示的数学关系。

为了便于下文的讨论，在满足公式（2）的条件下对m和n进行任意赋值，本文取m=8，n=6，即格雷码图像的最小编码周期占24个像元，而正弦相移周期占32个像元，此时，格雷码与正弦相移的非对称结合关系如图2所示。图中，所有格雷码周期边界均位于正弦相移区域中心位置，格雷码周期边界与正弦相移区域边界之间存在±4个像元的周期错位容错范围，用于避免格雷码码值与正弦相移区域码码值同时变化。需要指出的是，由于正弦相移和格雷码的非对称结合关系，k=0的格雷码周期边界并未与Pixel 0对齐，而是对应于N=0的正弦区域中间位置。

图2 展示了k=0～3的格雷码周期与正弦相移的非对称结合关系。k≥4时，格雷码周期与正弦相移的非对称结合关系依此循环。格雷码周期边界与正弦相移区域码的对应关系如表2所示。

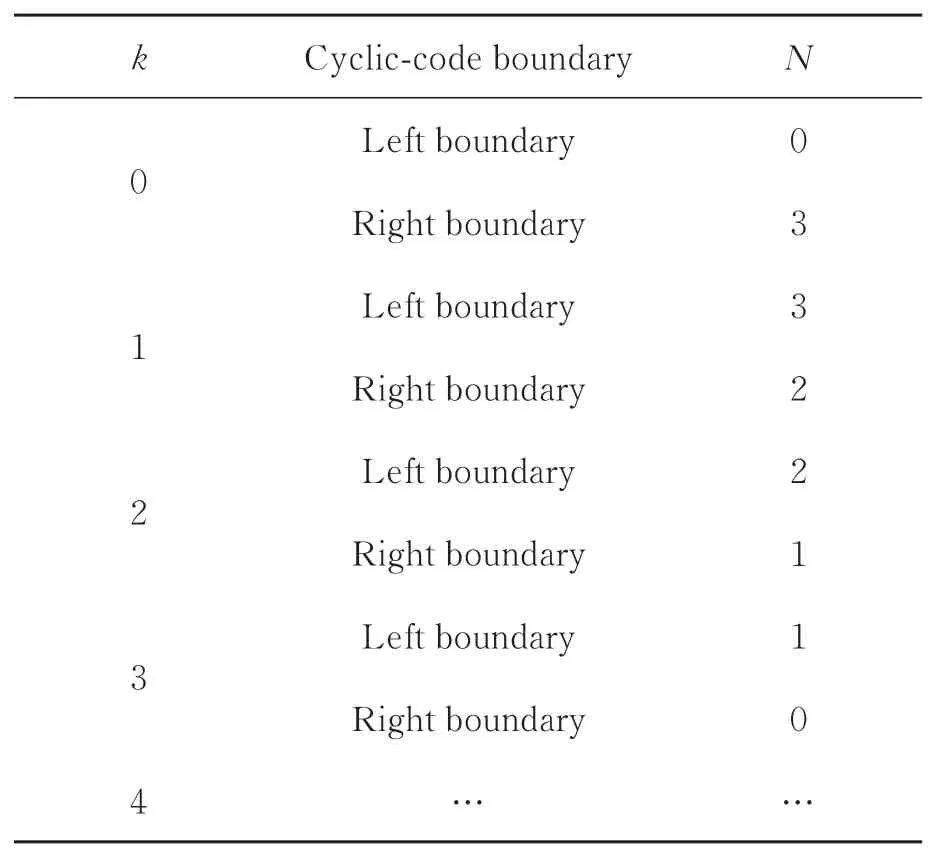
表2 格雷码周期边界与正弦相移区域码的对应关系Tab.2 Correspondence between the cyclic code boundar⁃ies and the region codes

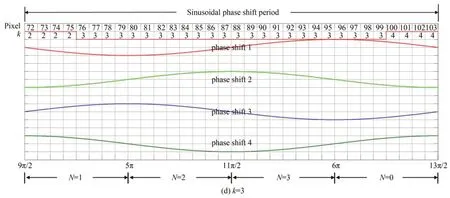
图2 格雷码与正弦相移的非对称结合关系Fig.2 Asymmetric combination of Gray code and sinusoidal phase-shift

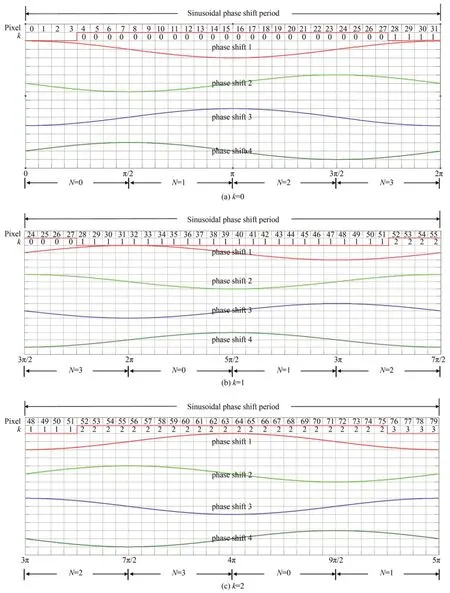
格雷码非对称结合四步正弦相移绝对相位Φ的解码需要考虑两者之间的非对称关系，解码方法如公式（3）所示，式中，k为格雷码码值，k=0，1，2…..31，N为正弦相移区域码，N=0，1，2，3，fix表示向下取整运算。

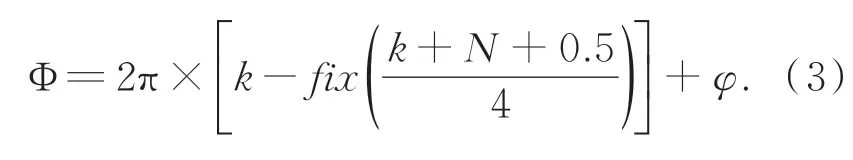
3 误差分析

3.1 ΔN和Δφ的关系

本文提出了正弦相移区域编码的概念和方法，并给出了与区域码N相关的相对相位的计算公式，我们将以图2（a）所示的编码为例，定量分析区域码误差ΔN与相对相位误差Δφ的关系，可能出现的误差情况如表3所示。对于经过辐射校正的测量系统，通过表1所示的编码规则判别正弦相移的区域边界时，判别误差通常可控制在一个像元，即正弦相移的区域码解码误差仅发生在区域边界的相邻像元之间。表3中，N代表区域码真值，N'代表带有误差的区域码测量值，N=0→N'=1代表区域码真值为0的边界像元被误判为区域码为1，φ代表相对相位的真值，φ'代表带有误差的相对相位测量值，Δφ代表相对相位的测量误差。

由以上分析可知，正弦相移的区域码产生一个码值的误差仅导致相对相位π/16的误差，对应编码图像中一个像元位置。

3.2 Δk、ΔN和Δφ的关系

由公式（3）可知，在格雷码周期边界附近，格雷码码值k和正弦相移区域码码值N的判读误差都将导致绝对相位Φ的展开误差。对于经过辐射校正的测量系统，正弦区域码边界和格雷码边界的判别误差通常可控制在一个像元，由于格雷码周期边界与正弦相移区域边界之间预留了±4个像元的容差范围，因此可认为格雷码码值与正弦相移的区域码码值不会同时出现判读误差。此时，可能存在的误差情况如表4所示，表中，k，N和Φ分别代表格雷码、区域码和绝对相位的真值，k'，N'和Φ'分别代表带有误差的格雷码值、区域码值和绝对相位值。

表4 △k、△N和△Φ的关系Tab.4 Relationship between△k，△N and△Φ

在各种可能的误差情况下，绝对相位的解算误差均等于相对相位的解算误差，由此可见，正弦相移非对称结合格雷码的编解码方法从原理上完全消除了周期错位误差的产生。

4 仿真验证

为了排除随机误差因素的干扰，在相同实验条件下准确地比较不同编码方法在周期错位误差抑制方面的性能差异，本文选择了仿真实验进行验证，仿真实验平台为3ds Max和MATLAB。仿真测量系统由摄像机、投影仪和被测物体组成。仿真摄像机模拟Nikon D850相机与105 mm焦距微距镜头的组合，其中相机CMOS传感器有效感光尺寸设置为35.9 mm×23.9 mm，传感器有效分辨率设置为8 256×5 504，105 mm焦距微距镜头的视场角度设置为23°20'；仿真投影仪模拟BenQ W7000 DLP投影仪，分辨率设置为1 920×1 080，投影区域设置为100 mm×56.25 mm，投影编码分别为传统格雷码结合正弦相移和格雷码非对称结合正弦相移，其中传统编码的最小周期占24像元，非对称结合编码的格雷码最小周期占24像元，正弦相移周期占32像元；摄影物镜和投影物镜位于被测表面同一侧，投影物镜光轴沿坐标系Y轴，投影中心距离坐标系原点O的距离为450 mm；摄影物镜光轴平行X-Y平面，与投影物镜光轴相交于坐标系原点O，呈15°夹角。

设置被测物体为一个理想平面，尺寸为100 mm×50 mm，表面反射特性为漫反射，被测平面沿X-Z平面放置，表面几何中心与坐标原点O重合，如图3所示。

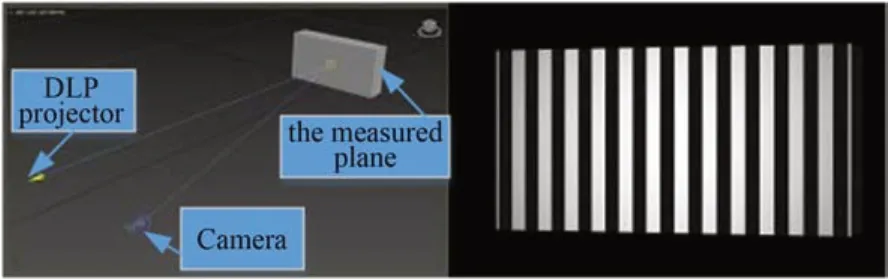
图3 理想平面的仿真测试Fig.3 Simulation measurement of ideal plane

分别应用对称结合编码配合周期误差校正的方法和非对称结合编码方法，对仿真环境下的理想平面进行测量，得到重构平面及其测量误差分别如图4和图5所示。

图4 应用对称结合编码配合周期误差校正方法的测量结果Fig.4 Simulation measurement results of plane with sym⁃metrically combined encoding and periodic disloca⁃tion error correction

图5 应用非对称结合编码方法的平面测量结果Fig.5 Simulation measurement results of plane with asymmetrically combined encoding

应用上述两种方法得到的平面测量数据如表5所示。从测量结果可以看出，应用传统对称结合编码方法配合周期错位误差校正算法的最大测量误差与均方误差相差巨大，说明部分像元位置的周期错位误差没有得到校正，或出现了校正错误；而应用非对称结合编码方法的最大测量误差与均方误差极其接近，说明周期错位误差已从原理上消除。

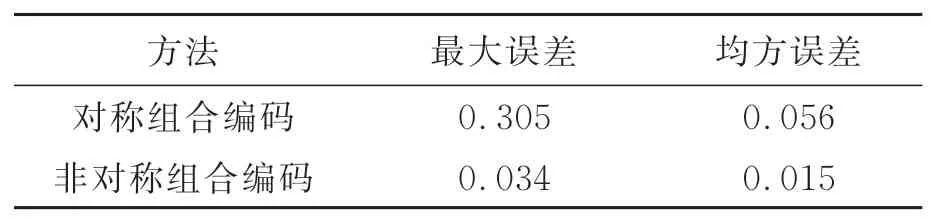
表5 对理想平面的仿真测量结果Tab.5 Simulation measurement results of the ideal plane（mm）

为了进一步验证格雷码非对称结合正弦相移编解码方法的可行性，本文对曲面进行了方针测试实验。设置被测物体为一个理想球体，球体半径为50 mm，表面反射特性为漫反射。球体几何中心与投影中心、摄影中心同高，且与O点重合，如图6所示。

图6 理想球面的仿真测试Fig.6 Simulation measurement of ideal sphere

分别应用对称结合编码配合周期误差校正的方法和非对称结合编码方法，对仿真环境下的理想球面进行测量，得到重构球面及其测量误差分别如图7和图8所示。

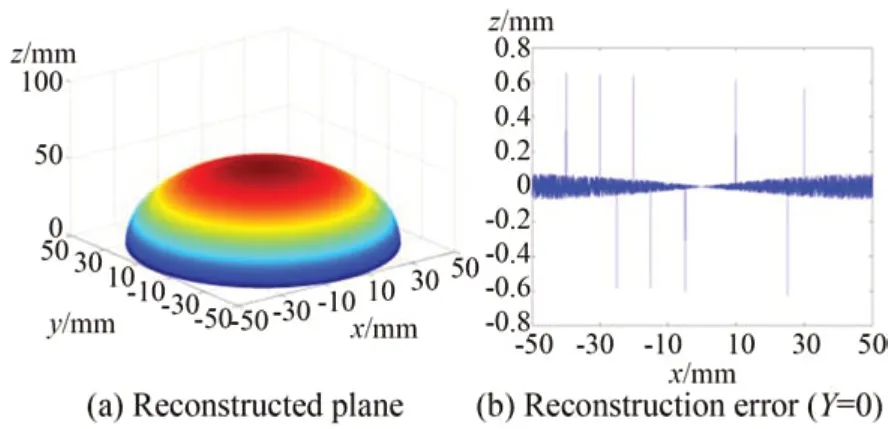
图7 应用对称结合编码配合周期误差校正方法的测量结果Fig.7 Simulation measurement results of sphere with symmetrically combined encoding and periodic dis⁃location error correction

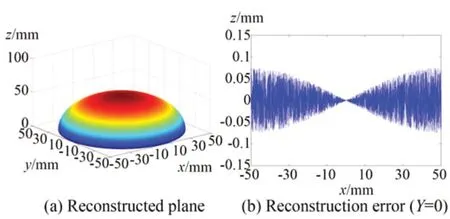
图8 应用非对称结合编码方法的球面测量结果Fig.8 Simulation measurement results of sphere with asymmetrically combined encoding

应用上述两种方法得到的球面测量数据如表6所示。从测量结果可以看出，应用传统对称结合编码方法配合周期错位误差校正算法的测量结果仍然存在显著的周期错位误差，且最大误差和较大误差的数量均较平面测量明显增加，这是因为在球面边缘位置，周期错位校正算法将部分正确的码值突变当做周期错位进行了错误的校正，导致了更多更大的解码误差；而应用非对称结合编码方法的最大测量误差和均方误差较为接近，说明非对称结合编码方法对周期错位误差的抑制效果仍然显著有效。

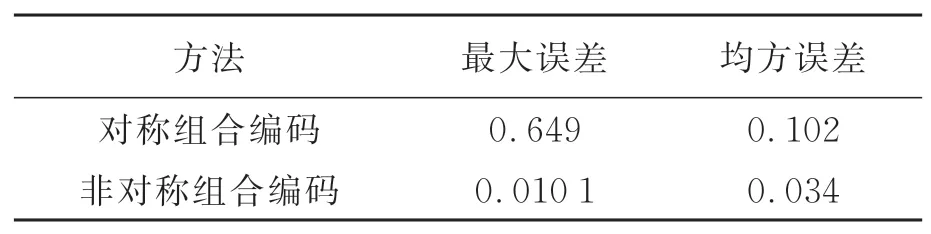
表6 对理想球面的仿真测量结果Tab.6 Simulation measurement results of ideal sphere（mm）

5 实验验证

为了进一步验证研究内容的正确性，以火星高分相机研制过程中加工的某精密平板作为测量对象，开展了实验验证工作。之所以选择最简单的平面物体作为实验验证对象，是因为相对于其他复杂表面，平面的精加工难度相对较低，加工保障的精度最高，便于定量比对和评价新技术的测量精度。待测平板尺寸为150 mm×100 mm×10 mm，其中一个150 mm×100 mm的表面进行了精密研磨，三坐标测量系统和粗糙度测试仪的测量结果显示：研磨后的表面粗糙度优于0.005 mm，平面度优于0.01 mm。使用BenQ W7000 DLP投影仪、Nikon D850相机与105 mm焦距微距镜头组建了测试系统，投影仪、相机和被测铝板之间的相对位置关系大体参照了第4章仿真实验的布局，但是并没有进行严格的约束，因此本文所采用的三维解算方法对测试设备的相对位置关系并没有严格的要求［27］。

应用本文提出的非对称组合结构光编码技术进行被测表面的重构，重构表面如图9（a）所示，将重构表面和拟合标准平面做差，得到测量误差如图9（b）、9和表7所示。我们可以发现，测试的最大误差和均方根误差大约为仿真结果的2倍，需要指出的是该误差既包含了测试系统的测试误差，也包含了被测表面的加工误差。可以确定是，测试过程中并没有产生类似图4（b）所示的周期错位误差，这表明本文提出的非对称组合结构光编码技术是正确有效的。

表7 对平面的测试结果Tab.7 Measurement results of plane （mm）

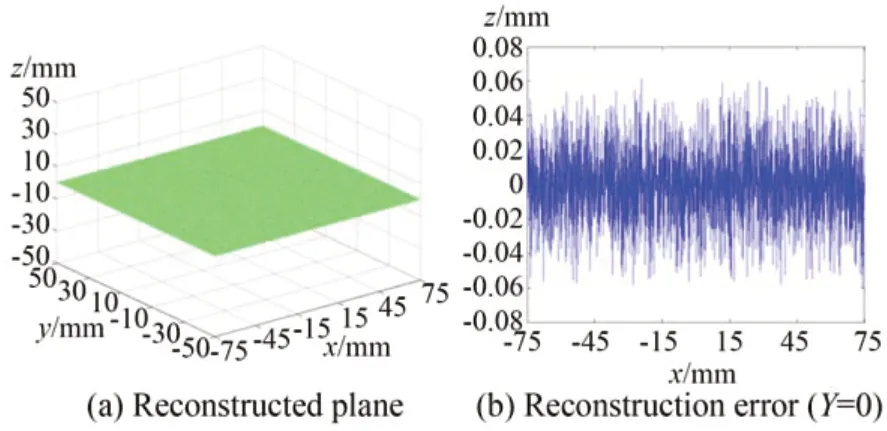
图9 实测结果Fig.9 Physical measurement results of plane with asym⁃metrically combined encoding

6 结 论

本文提出了正弦相移区域编解码的概念和方法，以及格雷码与正弦相移的非对称组合方法。3ds Max的仿真实验结果和实测实验结果显示，格雷码与正弦相移的非对称组合的编码方法有效地消除了周期位错误差，使最大测量误差减少了一个数量级，平均测量误差减少了70%，该方法比现有方法具有更高的测量精度、更高的测量密度和更高的测量效率，特别适用于高精度动态三维测量的应用场景。