基于直线空间旋转的十字结构光标定

秦训鹏，丁吉祥*，董寰宇，董书洲

（1.武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉430070；2.武汉理工大学 湖北省新能源与智能网联车工程技术研究中心，湖北 武汉430070）

1 引 言

线结构光测量以其非接触式且能获得较高的几何精度而在工业测量和三维重构领域得到广泛的应用［1］。在汽车与交通运输、航空航天等领域［2］，对于复杂曲面上特征检测问题一直是研究的热点问题，如汽车零部件制造与检测中螺纹孔的圆孔半径、圆心坐标和圆心位置度等都是质量检测的重要因素。而传统的人工测量不仅进度差而且效率低，如工业中测量使用的三坐标测量机等，无法满足现代生产线上的自动化要求。针对上述问题，国内外学者提出以结构光的形式进行测量。在线结构光测量系统中，相机标定精度和光平面标定精度是影响测量精度的主要因素。

传统的结构光标定方法有3D靶标法［3-4］、拉丝法［5］和消隐点法［6］等，但上述方法存在标定靶标复杂、标定点数量少、标定过程复杂和标定精度低等问题。邹圆圆等［7］设计一种标准量块作为标定靶标，简化了标定靶标对象，但需要三维精密平移台配合，标定过程复杂。陈天飞等［8-9］提出利用空间中平行直线与光轴不垂直时在摄像机中投影产生的多个消影点来完成光平面法向求解，避免了复杂靶标的使用，但是需要高精度运动机构来配合求解，由于这种限制，标定方法的可操作性会降低。杨凯等［10］提出一种基于自由移动平面靶标的标定方法，避免了运动造成精度降低和靶标过于复杂等问题，但标定点的数量较少，鲁棒性较差。于龙龙等［11］提出的基于二维平面靶标的线结构光标定，以直线方程的形式来表示光条图像信息，简化了标定靶标，弥补了标定点少的缺陷，但标定过程仍需移动靶标。然而针对十字结构光标定的研究，Kiddee等［12］提出了一种简单的CLSL（十字结构光标定）标定方法，以少量的十字光与靶标平面边线相交的非共线特征点来获取光平面方程，可以满足中等精度的测量需求，但标定点数量较少不能充分利用光条信息，同时还需要移动靶标来获取特征点，操作过程复杂。Zhang等人［13］采用十字结构光来进行焊缝识别测量，以光条中心点作为特征点来拟合光平面方程，最终测量的均方根误差在1.526 mm以内，标定精度还需进一步提高。

本文提出一种基于直线空间旋转的十字结构光平面标定，利用靶标平面内光条直线的空间旋转特性来获取光平面拟合所需直线，不仅增加特征点数量，而且不需再次移动来获取光条中心点即可完成光平面标定，既提高了精度，又可使标定的过程更加便捷。

2 十字结构光视觉测量模型

十字结构光视觉测量模型采用相机垂直布置、结构光发射器倾斜布置的结构方式，为保证光条中心点的提取精度，十字结构光入射中心线与水平面的夹角要保证在30°~60°之间，取相机光轴与激光投射中心线所成夹角为45°，且所成平面位于X w Y w Zw平面内，相机坐标系原点到光轴与结构光平面交点的距离为L，其模型示意图如图1所示。其中Oc-X cY c Zc为相机坐标系，OXY为图像坐标系，Oc为摄像机的光轴中心，在靶标平面E上的投影点为O w，以图像坐标系中的X和Y轴为正方向，以右手准则建立世界坐标系Ow-Xw Y w Zw。

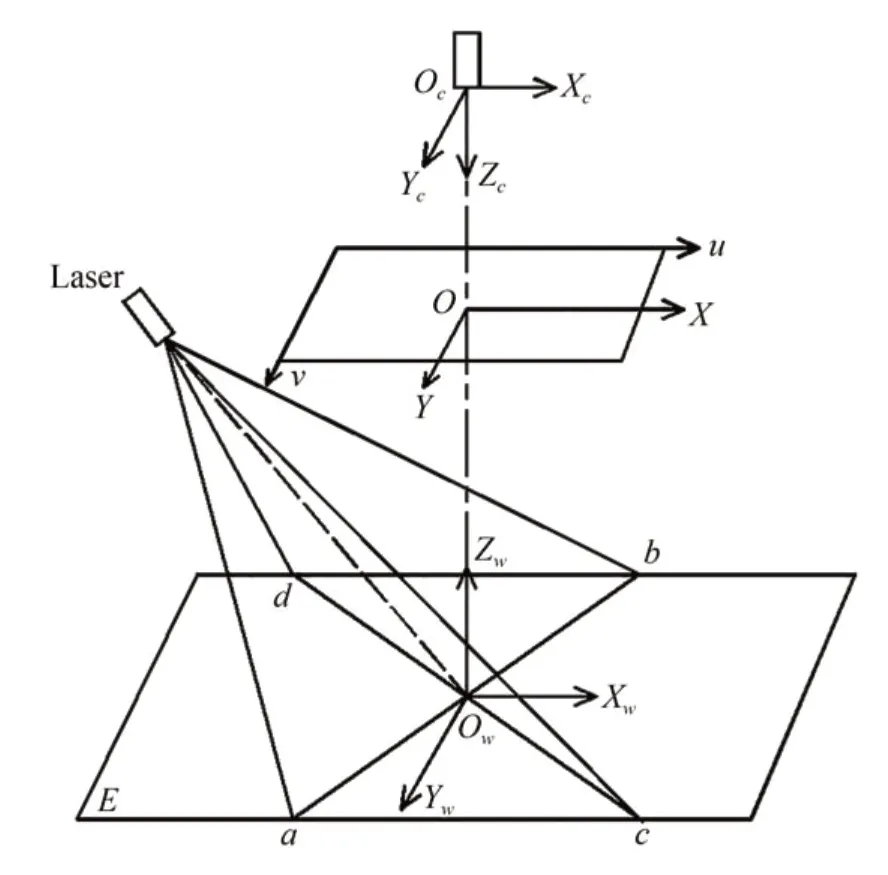
图1 十字结构光视觉测量模型Fig.1 Cross structured light vision measurement model

根据相机的针孔成像模型和世界坐标系与相机坐标系之间的变换关系［14］，将图像像素坐标系下的坐标进行射影变换，并建立其与世界坐标系下对应点的转换关系［8］。

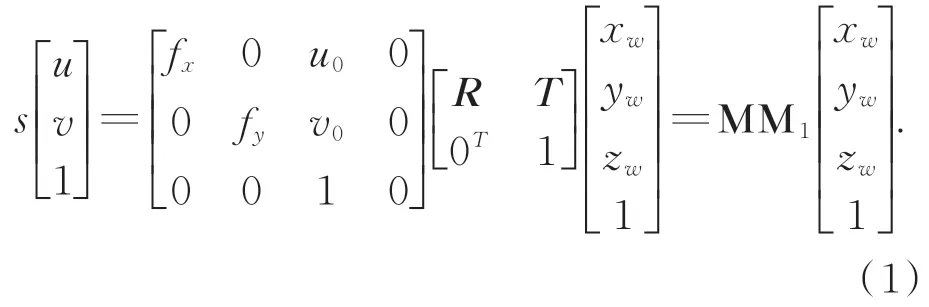
其中：s为比例因子，（u，v）为图像坐标系中点的像素坐标，M为相机的内参矩阵，其中fx，fy分别为相机在x，y方向上的有效焦距，u0，v0为图像坐标系下光心坐标，M1为相机的外部参数矩阵，R和T代表世界坐标系与相机坐标系之间的旋转和平移矩阵。

相机坐标系下，光平面方程的表达式为：

其中，A，B，C，D为待标定的光平面方程系数。

在上述理论的基础上，本文提出一种十字结构光标定算法，算法流程如图2所示。

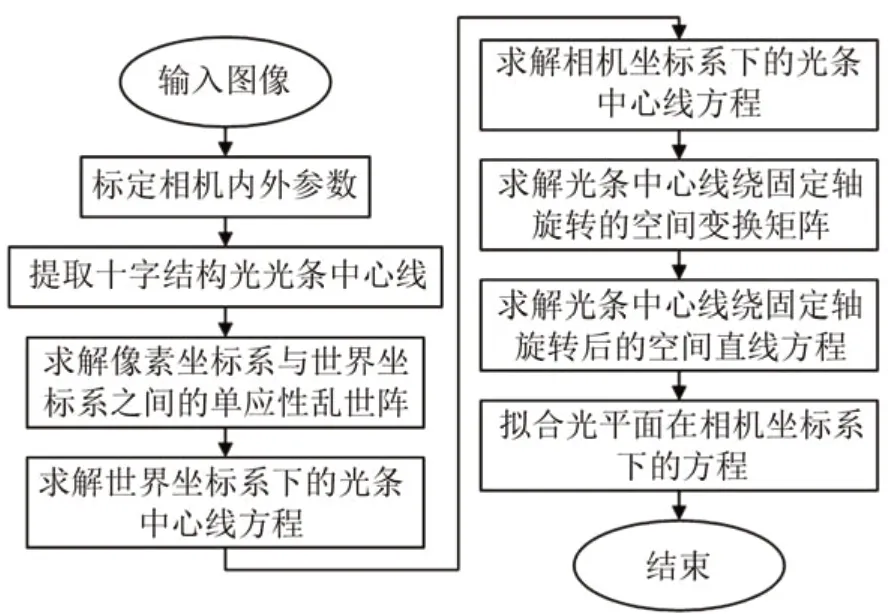
图2 十字结构光平面标定算法流程Fig.2 Cross structured light plane calibration algorithm

3 十字结构光平面标定

3.1 十字结构光光条中心提取

在实际测量实验中，十字结构光在物体表面所呈现的光条具有一定的像素宽度，需要采用一种合适的光条中心提取算法来获取中心点像素坐标，并以光条中心点坐标作为十字结构光的实际投射位置。如图3所示，为快速、精确地提取图中特征光条的中心点坐标，对矫正后的图像提取感兴趣区域（ROI）和用高斯滤波去除图像中的干扰噪声，其次采用OSTU算法以及基于Hes⁃sian矩阵的Steger算法［15］提取光条中心。通过OSTU算法设置合适的灰度阈值，提取出光条图像所在区域，可以提升后续十字结构光中心的提取速度。通过Hessian矩阵获取特征光条的法线方向，在法线方向上对光条截面的灰度值进行泰勒展开，进而求取光条在截面上的一阶零点，即灰度的极大值点，作为光条在该法线方向上中心点。该算法在一定程度上能够减少图像中一些由物体表面产生的漫反射光对光条中心提取的影响，具有较好的鲁棒性和稳定性，且能达到亚像素级提取精度。

图3 十字结构光灰度图Fig.3 Cross structured light grayscale image

3.2 基于单应性矩阵的空间直线方程求解

针对上述提取的光条中心点坐标进行最小二乘拟合，求得直线在相机像素坐标系下的直线方程，将其转换为齐次表达式为：

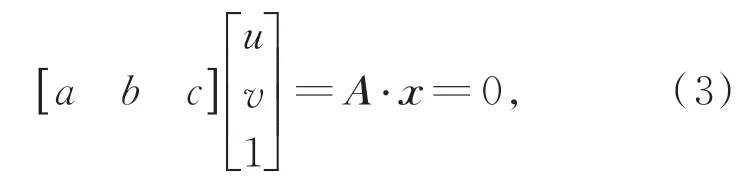
其中，A为图像平面内直线方程的系数矩阵。

而在射影变换中，对于满足中心投影映射的两个平面，存在单应性矩阵H使得像平面和靶标平面上的点满足如下关系［11］：

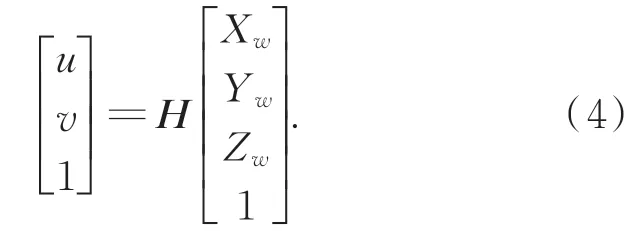
为获取两平面之间的单应性矩阵H，首先使用相机拍摄标定靶标图像，并通过角点提取算法提取靶标图像中的所有圆心坐标，如图4所示，我们定义靶标中间的圆心坐标为世界坐标系原点，且靶标所在平面Zw=0，采用Ransac算法对圆形靶标在像平面内的圆心坐标和在世界坐标系内的坐标进行匹配求解，最后通过L-M优化算法得到单应性矩阵H。相比于使用四对匹配点计算单应性矩阵，本算法由于采用了圆形靶标上的所有圆心特征点坐标来计算单应性矩阵，计算的结果鲁棒性更好。

图4 靶标图Fig.4 Image of target

根据式（3）和（4）的求解结果，可得两平面上直线方程的变换关系为：

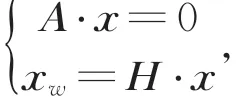
即：

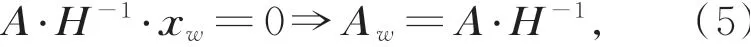
其中，A w为靶标平面内的直线方程系数矩阵。通过上述图像坐标系下直线拟合得到的直线方程便可以求解出对应靶标平面上的光条中心线方程。

根据靶标平面所在的世界坐标系与相机坐标系的转换关系［10］知：

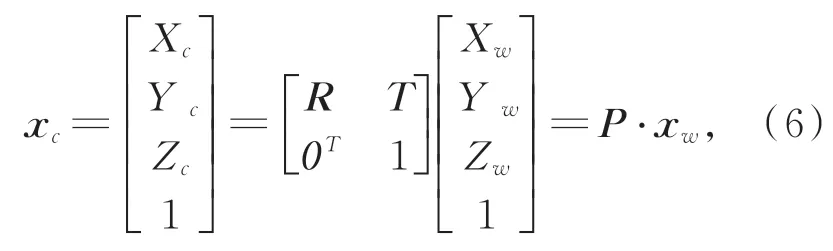
其中，P为空间中的一点从世界坐标系到相机坐标系的位姿转换矩阵。

根据式（6），进一步可得在相机坐标系下直线方程为：

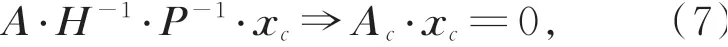
其中，A c是靶标平面上的直线在相机坐标系下的直线方程系数。

3.3 基于空间直线旋转的直线方程求解

根据十字结构光平面∏1和∏2与靶标平面相交产生的两直线在相机坐标系下的空间直线方程，可得两直线的交点O1为（Xc，Y c，Zc），相对应的在与相机光心同一高度处的一点O2坐标为（Xc，Y c，0）。通过将O2点绕O1点沿Xc轴反向旋转α度，可得激光器的入射方向，取入射方向上一个入射点F，其坐标为（X c-Zctanα，Y c，0），其中α为激光器入射方向与靶标平面夹角。

对于三维空间中的任意一点M（mx，my，mz）和空间直线L，直线的单位方向向量为n（nx，ny，nz），且经过点Q（x0，y0，z0），如图5所示。

图5 空间点绕任意轴旋转Fig.5 Rotation of space points around any axis

旋转轴线L在坐标系下的直线方程为：

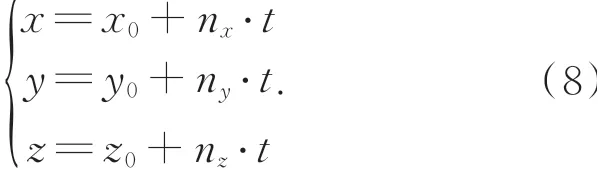
圆弧MM'旋转所成平面在坐标系O-XYZ下的平面方程为：

根据式（9）和（10）可以求得：

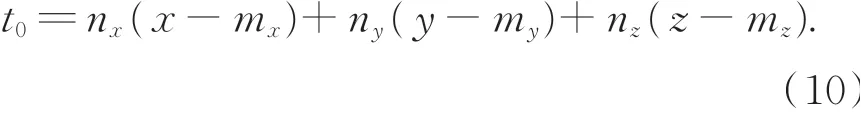
设圆弧MM'的圆心在坐标系O-XYZ下的坐标（xc，yc，zc）为：

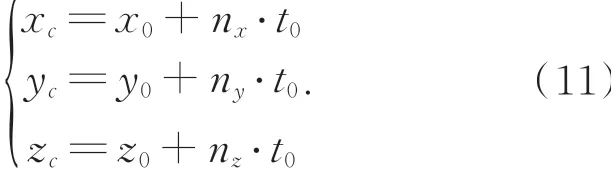
圆半径r为：

点M'在坐标系o-x'y'z'上的坐标为：

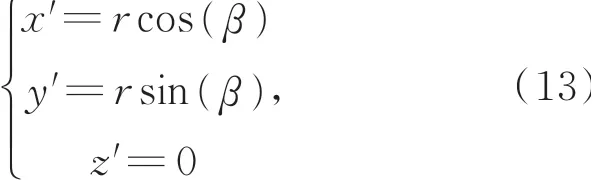
其中，β为点M绕旋转轴线L的旋转角度。利用齐次坐标变换，将点M'在坐标系o-x'y'z'的坐标变换到坐标系XYZ的坐标：

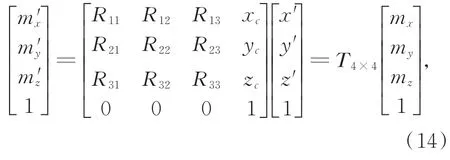
其中：T4x4为空间变换矩阵，K=1-cosα，G=

根据空间直线旋转变换关系，光平面∏2与靶标平面相交产生的光条的中心直线绕轴线FO1旋转180°后得：

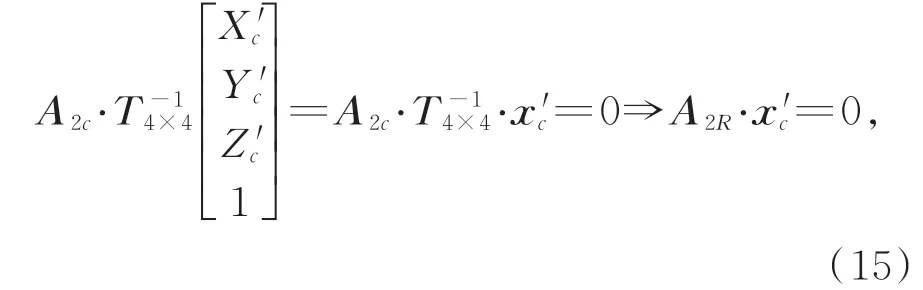
其中，A2R为光平面∏2中的直线旋转后的直线方程

系数矩阵。进一步可得靶标平面内的光条中心线从图像像素坐标系到相机坐标系的变换关系为：

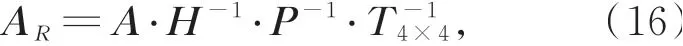
其中，A R为相机坐标系下，靶标平面内任意直线绕固定轴旋转后的直线方程系数矩阵。

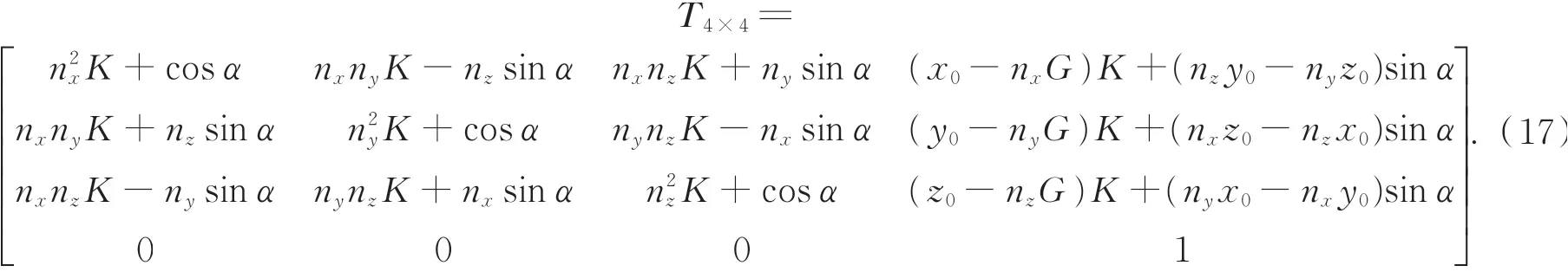
3.4 十字结构光平面方程求解

根据上述相机的透视变换模型和空间直线的旋转变换关系，靶标平面内的光条中心线绕入射中心线旋转180°后的直线与旋转前的直线位于同一光平面内，以最小二乘法拟合两条直线便可以得到光平面方程，即：

其中，平面∏1的法向量n1=（A1，B1，C1），平面∏2的法向量n2=（A2，B2，C2）。以上为整个十字结构光平面的标定过程，完成相应参数的求解即可完成光平面标定。

4 实验验证与分析

搭建十字结构光测量系统如图6所示。激光器采用的是波长为650 nm的十字激光器，功率为100 mW，相机选用Basler公司的面阵相机，镜头选用的是Ricoh 8 mm定焦镜头。选取圆形靶标标定板，标定板由7×7个实心圆阵列组成，圆形直径为3.5 mm，相邻两个圆形之间的圆心距离为7 mm，外框黑线尺寸为56×56 mm圆点标定板的制造精度为±0.01 mm。

图6 十字结构光测量实验系统Fig.6 Cross structured light measurement experiment system

在标定过程中，对标定板的识别和建立坐标系时，以标定板的左上缺角为准，以正中圆心为坐标原点，左侧同行圆点中心线为X轴，下侧同列圆点中心线为Y轴，以正中圆心垂直于标定板平面为Z轴，建立靶标平面坐标系，如图7所示。

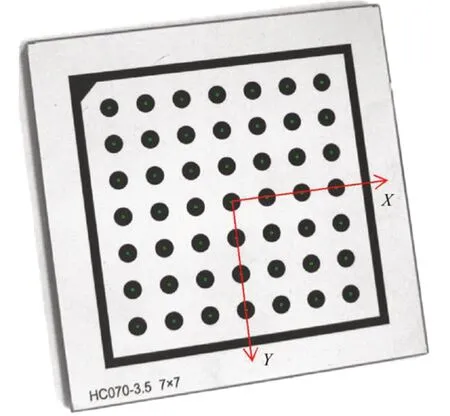
图7 靶标平面坐标系Fig.7 Target plane coordinate system

4.1 相机标定

利用工业相机采集24幅不同位置处的标定板图像。对所采集的24幅标定板图像，利用opencv中的标定模块，对每幅标定板图像中的所有圆形靶标进行圆心提取。利用圆形靶标圆心的亚像素级像素坐标和张正友标定法［16］，即可得到相机的内、外部参数和畸变系数的最优解，其标定结果如表1所示。根据上述参数计算标定点在靶标平面上的重投影误差的均值为0.06 pixel，使用的相机具有较高的标定精度。

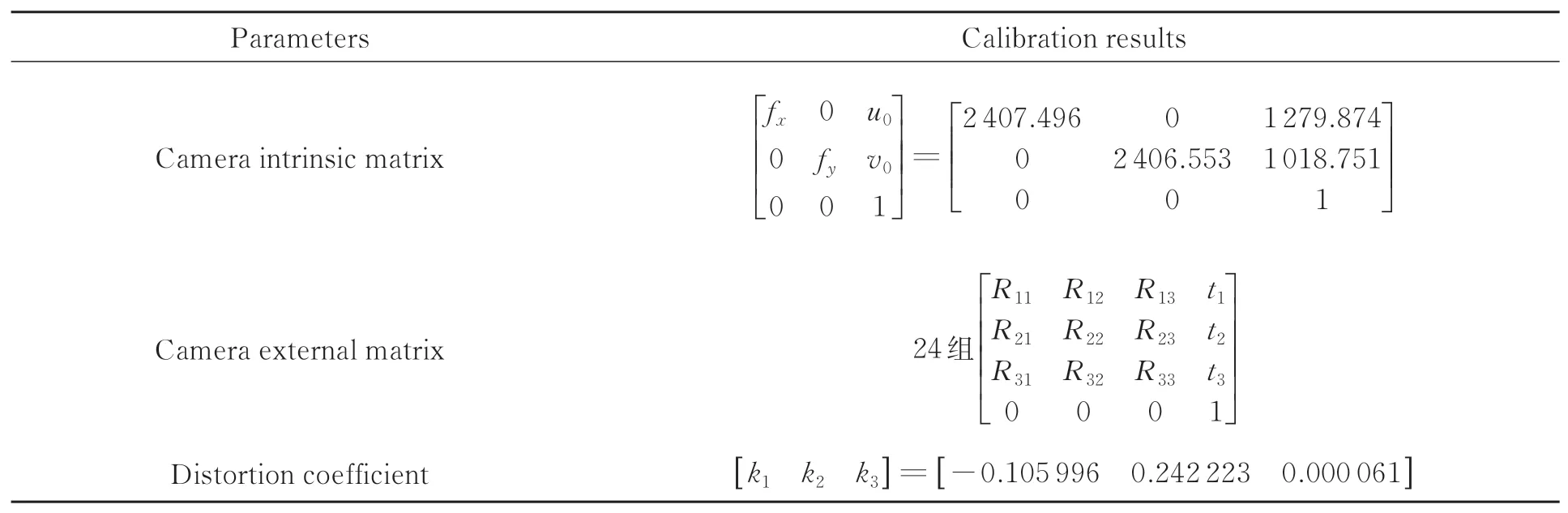
表1 相机标定结果Tab.1 Camera calibration result

4.2 十字结构光平面标定

以第一幅标定板中的靶标平面坐标系为世界坐标系，进行十字结构光平面标定。光条中心提取结果如图8所示。利用单应性矩阵和坐标变换矩阵，获取相机坐标系内的光条直线方程如图9（a）所示，绕固定轴线进行旋转如图9（b）所示。光平面拟合结果如图10所示，获得两个光平面∏1和∏2的方程为：

图8 光条提取结果Fig.8 Light strip extraction results

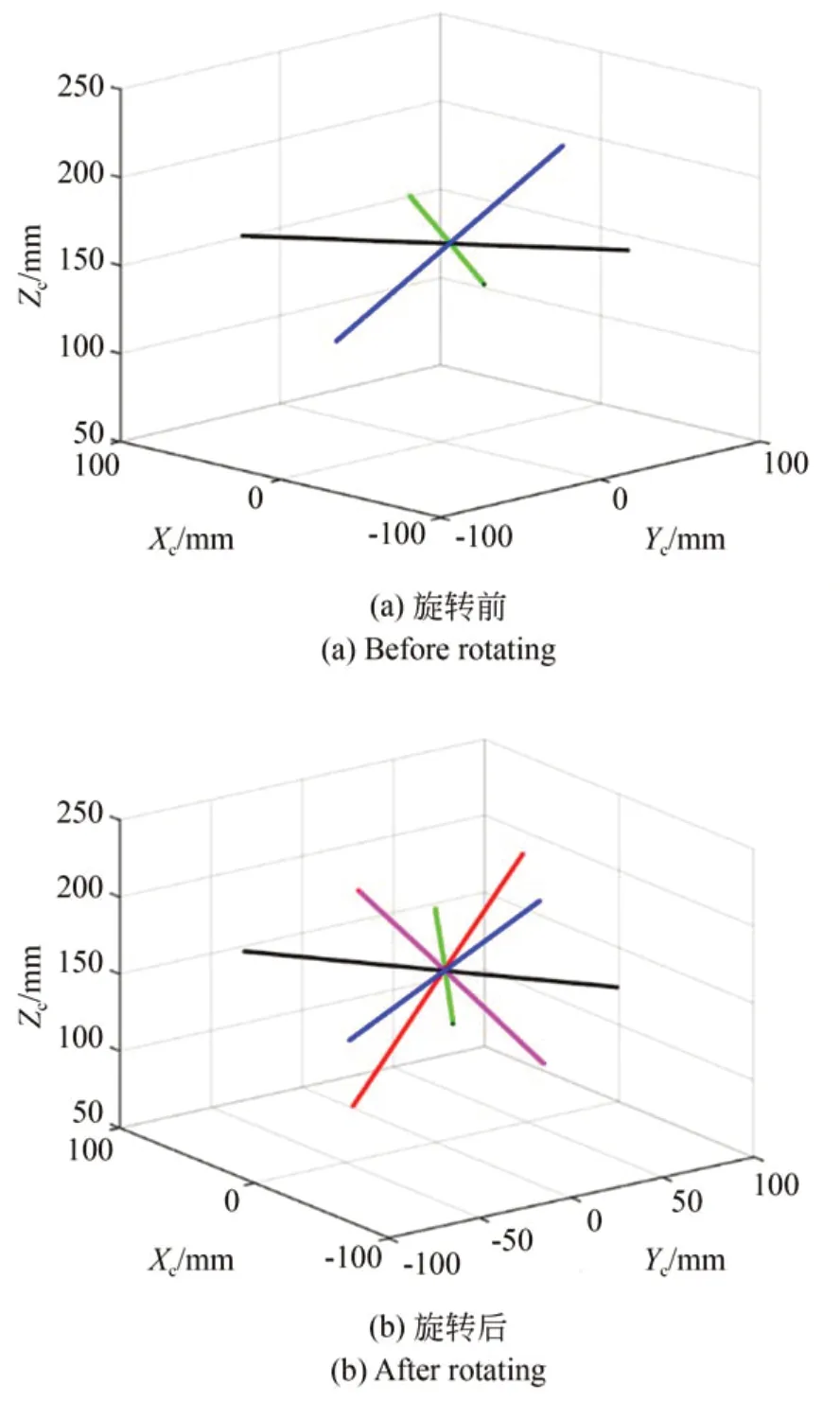
图9 直线空间旋转变换Fig.9 Linear space rotation transformation

图10 光平面拟合Fig.10 Light plane fitting

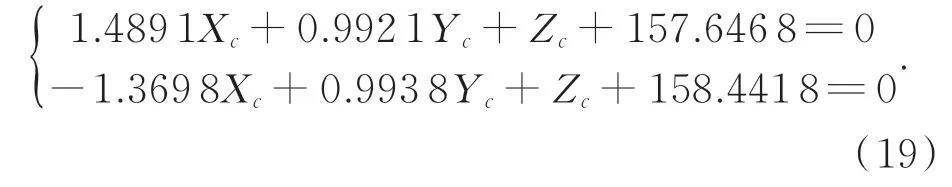
4.3 精度分析与对比实验

为验证上述标定方法标定结果的准确性，将靶标随机放置在相机坐标系下的不同高度处，进行光平面标定，对标定后两光平面的夹角α进行计算，实验结果如表2所示。

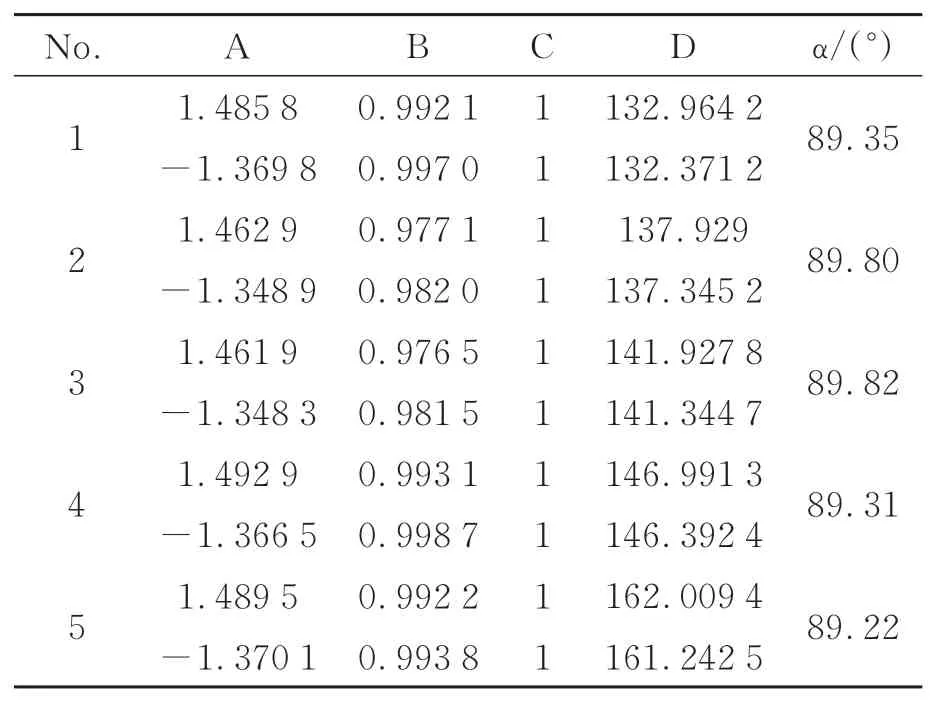
表2 不同位置标定结果Tab.2 Calibration results at different positions

由表2可知，不同高度处的光平面夹角误差在1°以内，满足标定精度要求。

如图11所示，计算每条光条中心直线与每行圆心坐标拟合的直线的交点坐标以及夹角，通过计算相邻两交点之间距离的正弦值与标准值的误差来评估精度。采用交比法［17］和本文方法对靶标在相机坐标系下不同高度处的圆心间距测量结果如图12所示，表3为同一位置处两种方法对圆心间距的测量结果。

图11 靶标圆心间距测量Fig.11 Target distance measurement

根据图12，本文标定方法得到的测量误差整体上优于交比法得到的测量误差，其中本文方法测量的平均绝对误差为0.023 mm，均方根误差为0.026 mm，交比法测量的平均绝对误差为0.035 mm，均方根误差为0.037 mm。根据表3，对于同一位置处圆心间距的测量，使用本文的标定方法测量的平均绝对误差为0.025 mm，均方根误差为0.029 mm，而交比法测量的绝对误差为0.036 mm，均方根误差为0.039 mm。

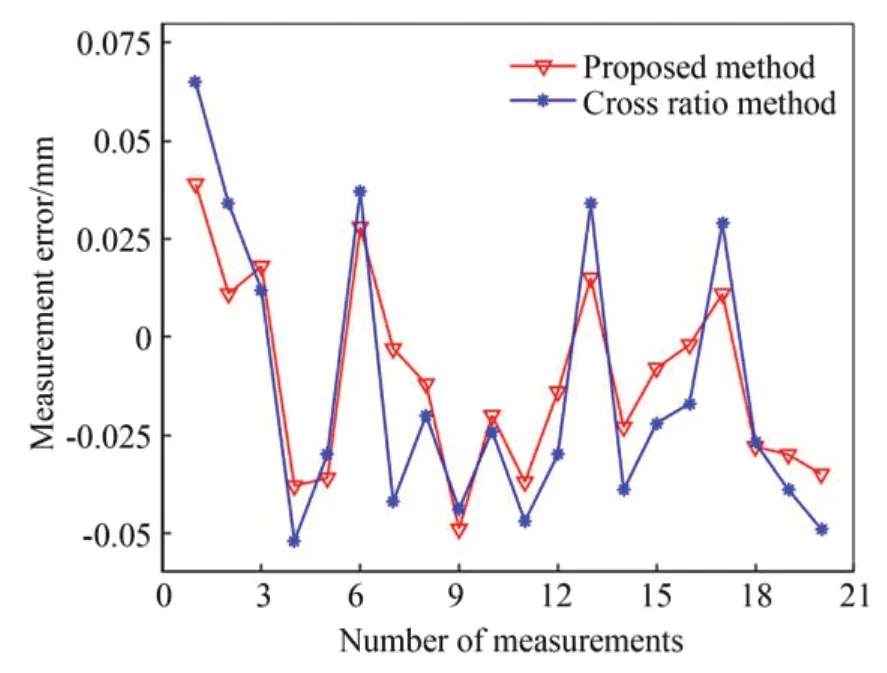
图12 两种标定方法的测量误差Fig.12 Measurement errors of two calibration methods

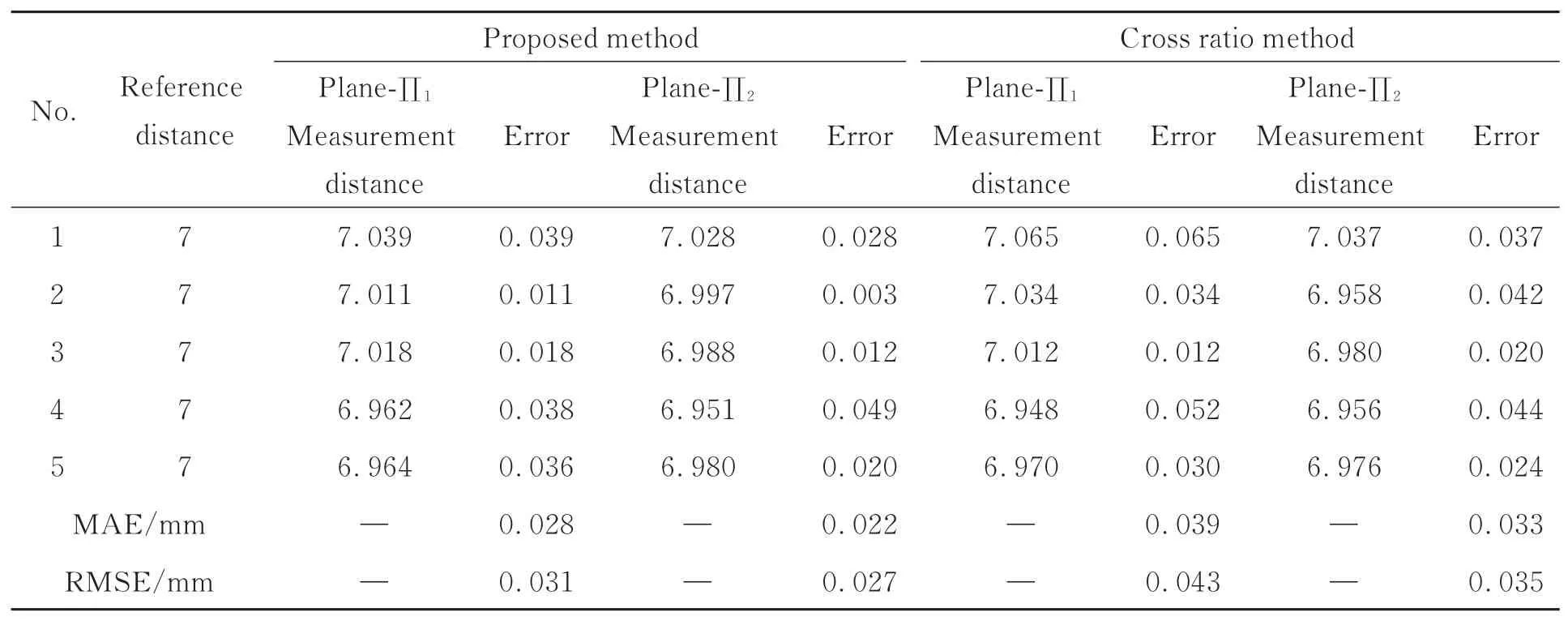
表3 同一位置不同方法测量结果Tab.3 Measurement results of different methods at the same location （mm）

影响测量精度的因素有很多，包括：光条中心提取和拟合准确度、测量物体表面反光特性、机械载体以及实验器材的制造误差等。本文所述标定方法，不需要多次对光条中心进行提取和拟合，也不需要配合机械运动来获得另一平面内的十字结构光中心线，因此可以减小光条中心拟合次数造成的累积误差以及机械运动误差对测量精度的影响。通过上述实验的误差对比可知，本文方法比交比法更能获得较高的标定精度，更加符合测量要求。

5 结 论

本文针对十字结构光平面的快速、高精度标定，提出一种基于直线空间旋转的十字结构光平面标定方法。利用拟合后的光条中心直线，结合单映性矩阵和世界坐标系与图像坐标系之间的旋转变换矩阵，来获取相机坐标系下的直线方程，通过直线绕任意轴的旋转变换关系，将直线进行旋转，拟合相应平面内的直线即可完成光平面标定。该方法以直线替代特征点，同时剔除光条提取过程中的异常数据点，不需要复杂的空间特征点求取，标定的鲁棒性更好，且标定过程不需要再次移动靶标平面，标定过程更加简单。实验结果表明，本文方法对圆心间距测量的平均绝对误差为0.023 mm，均方根误差为0.026 mm，测量精度优于传统标定算法，且满足大多数工件的测量精度需求。