工艺误差影响下微电热驱动器失效分析

陈 浩，曹 云，王新杰，王 炅，席占稳，聂伟荣

（南京理工大学 机械工程学院，江苏 南京210094）

1 引 言

微机电系统（Micro Electro Mechanical Systems，MEMS）微电热驱动器利用焦耳热效应产生热形变实现位移［1］，是一种较为可靠的驱动方式。相对于压电［2］、静电［3］、磁致［4］等驱动器而言，电热驱动器具有输出位移大、输出力稳定以及工艺兼容性好等优点。但MEMS工艺中存在的不确定性会导致电热驱动器实际测量得到的参数与设计参数产生较大的偏差。这些随机偏差不仅影响驱动器的性能，而且严重降低了驱动器的工作可靠性，甚至导致其失效。

目前关于MEMS随机工艺误差的诸多研究主要分为以下三种方式。第一种方式：定性研究单一工艺误差与结构性能之间的关系［5-7］。例如，曹云等人［5］研究了弹簧线宽、厚度、侧壁倾角和两电极间隙等单一尺寸误差对万向惯性开关阈值的影响。第二种方式：采用统计方法模拟得到工艺误差下结构性能的概率分布［8-9］。例如，J.S.Kong等人［8］对静电驱动器中的尺寸误差进行随机抽样，通过有限元仿真计算每个样本点所对应的位移，最终得到静电驱动器存在加工误差时的位移统计规律。第三种方式：建立结构性能关于参数的随机数学模型，量化工艺误差对结构性能的影响［10-12］。例如，Lili Gao等人［10］采用侵入式混沌多项式展开法（Intrusive Polynomial Chaos Expansions，IPCE）分别建立了MEMS微梁的弹性模量和应力关于加工误差的模型，分别得到弹性模量和残余应力的概率分布密度并通过蒙特卡洛法进行验证。由于MEMS器件性能是多个工艺误差同时作用的结果，采用第一种分析方式不能全面地反映误差对器件性能的影响。而基于统计原理的分析方法为了保证结果的全面、准确需要进行大量的随机抽样，从而造成计算时间成本的成倍增加。混沌多项式展开方法兼顾了结果精度与计算成本，因此是一种行之有效的工艺误差不确定性分析方法。

混沌多项式展开法（Polynomial Chaos Expansions，PCE）基于混沌多项式理论，能精确描述任意特征分布的随机变量的随机性［13］。非侵入式混沌多项式展开法在进行随机分析时，只需在系统输入和输出两者之间建立一种映射关系，因此无需知道系统响应函数的具体形式。侵入式混沌多项式展开法会改变原有的系统响应函数形式，从而根据新的系统响应函数得到输出的随机分布［14］。本文提出一种非侵入式混沌多项式展开方法（Non-intrusive Polynomial Chaos Expansions，NIPCE）用于V型微电热驱动器中点处的温度的不确定性量化及整体结构失效概率研究。本文具体研究步骤如下：首先通过对加工工艺分析，确定微电热驱动器的主要参数的误差来源；其次对加工样品的主要参数进行测量并分析得到误差下参数的特征分布；接着将参数作为变量，构建微电热驱动器中心点处温度的混沌展开多项式，并使用蒙特卡洛法对混沌多项展开模型进行验证；最后对混沌多项展开模型进行分析，得到V型微电热驱动器发生温度失效的概率。

2 器件制作工艺

硅基MEMS电热驱动器主要采用干法深刻蚀即反应离子深刻蚀工艺（DRIE）制作。以光刻胶为牺牲层、硅片作为器件结构，进行多次掩膜、光刻、刻蚀及去胶等步骤［15-17］，如图1所示。

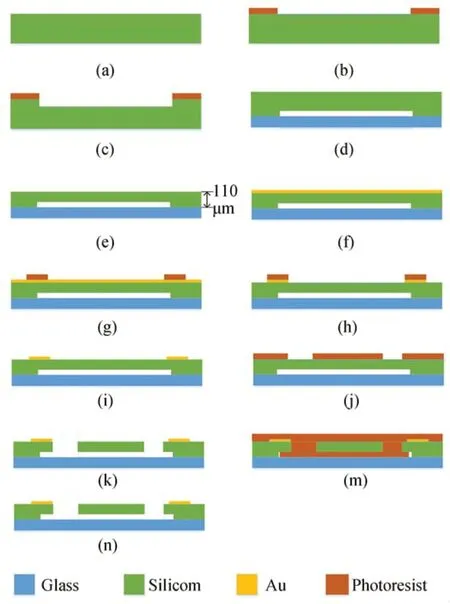
图1 硅基电热驱动器的制作流程Fig.1 Fabrication process of the silicon-based electrothermal actuator

（a）备片：选择晶面为（100）的硅片，经掺杂处理后，硅片的电阻率降低到0.01～0.02Ω·cm，并对硅片进行清洗；（b）光刻；（c）刻蚀：深刻蚀8～10μm，得到硅片锚点，清洗去除光刻胶；（d）非对准键合：采用7740玻璃片与硅片锚点键合；（e）减薄：采用KOH溶液对硅片背面进行湿法刻蚀，刻蚀后的硅片整体厚度约为110μm，从而满足微电热驱动器厚度设计要求；（f）溅射：在硅片表面溅射、淀积一层Ti/Au合金薄膜；（g）光刻；（h）刻蚀：对合金层进行刻蚀，从而形成电热驱动器电极，清洗除胶；（i）合金化：使合金与硅片之间形成低欧姆接触，同时也增加合金与硅之间的附着力；（j）光刻；（k）刻蚀：采用反应离子刻蚀释放结构得到电热驱动器；（m）划片：涂胶保护结构进行划片；（n）清洗：使用丙酮溶液去除保护胶，最终完成器件制作。对制作样品进行分选；准备合适的印刷电路板（PCB）；使用红胶进行粘片；经烘干、引线；最终完成微电热驱动器的封装，如图2所示。

图2 微电热驱动器的封装样品Fig.2 Packaged sample of the micro-electro-thermal actuator

3 误差测量及其特征分布

V型电热驱动器结构示意图，如图3所示。采用高倍显微镜（OLYMPUS STM 6）和欧姆表，对同一加工批次的23个样品分别进行了主要参数的测量，分别测量了电热驱动器的宽度与电阻。所有样品参数的测量结果如图4所示。从图中可以看出：驱动器宽度和电阻的偏差较大，宽度的变化范围为：33~39μm，电阻的变化范围为：130~170Ω。等离子深硅刻蚀工艺（DRIE）中，刻蚀区域深宽比越小，刻蚀速率越快。在本次加工的整体结构中，各部分的刻蚀宽度相差较大，而V型电热驱动器刻蚀区域的深宽比较小，其刻蚀速率较快导致过刻蚀的产生。此外，由于V型驱动器在硅片上均匀分布且硅片中间和边缘处的刻蚀速率不一样，因此硅片不同位置处的驱动器的过刻蚀时间不同。综上，V型电热驱动器样品的宽度误差较大。对于驱动器电阻而言，由于掺杂工艺中的不均匀性，导致硅片不同区域的电阻率也不同，因此在驱动器宽度和电阻率误差的共同作用下，其电阻的偏差也会较大。

图3 V型电热驱动器结构示意图Fig.3 Sketch of the V-shaped electro-thermal actuator

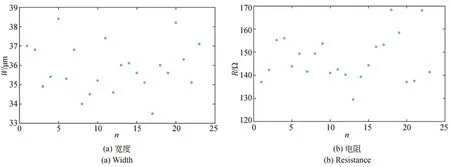
图4 各个样品参数测量结果Fig.4 Measuring result of the parameters in the samples

样品的电阻值不仅与材料电阻率有关，也取决于驱动器的尺寸参数。电阻与宽度之间的相关性增加了可靠性分析的复杂性。因此独立变量电阻率ρ更适用于建立可靠性分析模型。根据（1）式，可计算得到每个样品的电阻率值。

其中h为驱动器的厚度。由于在加工过程，对硅片进行整体减薄以保证驱动器的厚度（100μm），因此在电阻率计算中各样品驱动器的厚度可视为恒定值。因为V型电热驱动器单臂长度l达到1 500μm，所以其相对误差要远小于宽度w的相对误差。因此计算时可忽略长度的尺寸误差对电阻率的影响。经过计算，得到各个样品中的电阻率如图5所示。

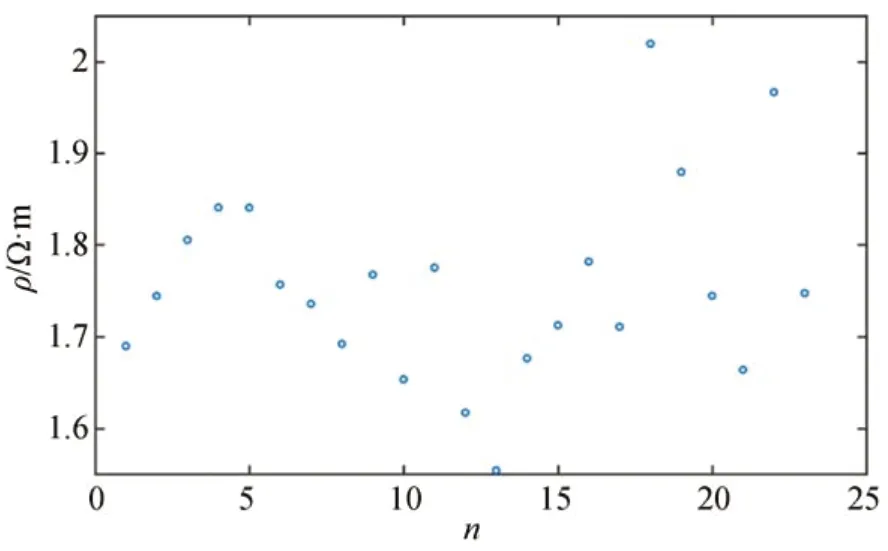
图5 各个样品的电阻率Fig.5 Resistivity of the samples

电阻率是材料固有属性，因此实际与驱动器尺寸无关，而在掺杂工艺中，离子注入浓度满足：

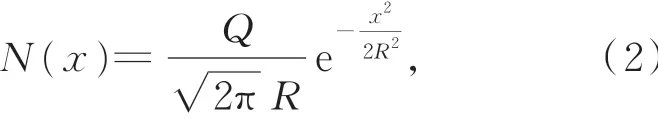
其中：Q为注入离子束剂量，R为掺杂半径。从该式可以看出：硅片不同区域的电阻率满足正态分布。由于V型电热驱动器均匀分布在硅片上，因此驱动器的电阻率应具有正态分布特征。为进一步建立混沌多项式展开模型，这里假设V型驱动器的宽度满足正态分布。通过对所测量到的数据散点分别进行拟合，得到宽度和电阻率所满足的正态分布累计密度函数曲线，如图6所示。从图中可以看到：拟合得到的正态分布能较好地描述宽度和电阻率的误差分布特征。表1给出了电热驱动器测量样品宽度和电阻率的一阶和二阶统计矩（均值、方差）以及拟合得到的正态分布特征参数。

图6 宽度和电阻率累积密度函数曲线Fig.6 Cumulative density function（CDF）curve of width and resistivity

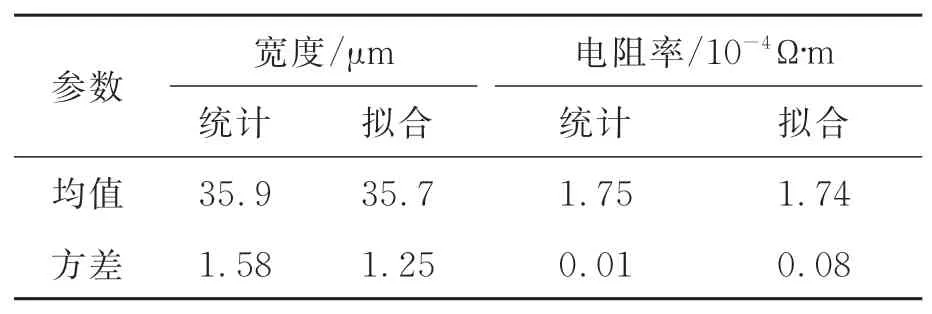
表1 驱动器宽度和电阻率的一、二阶统计矩及拟合得到的正态分布参数Tab.1 First and second order statistical moment and pa⁃rameters of normal distribution by fitting of width and resistivity in the actuator

4 非侵入式混沌多项式展开

在微电热驱动器中，不仅涉及多物理场耦合而且存在特殊的热损失形式，导致微电热驱动器的温度方程十分复杂，因此宜采用非侵入式混沌多项式展开法对电热驱动器的温度进行不确定性分析。基于非侵入式混沌多项式展开法的V型微电热驱动器温度分析流程如图7所示。

图7 基于非侵入式混沌多项式展开法的驱动器温度不确定性分析流程Fig.7 Stochastic analysis of temperature on the actuator based on non-intrusive chaos expansion method

4.1 模型构建

通过上述对V型驱动器宽度和电阻率的测量分析，由于宽度和电阻率存在误差，驱动器温度分布也相应地存在不确定性。V型电热驱动器最高温度存在于驱动器的对称中心处［18］。基于非侵入式混沌多项式展开方法，建立该处温度关于宽度和电阻率的数学模型，进而可以分析V型电热驱动器温度失效概率。由变换公式（2），变量宽度和电阻率转化成标准正态分布。

其中：ψ为变换前的变量，满足正态分布N（µ，σ）；ζ为变换后的变量，满足标准正态分布N（0，1）。根据非侵入式混沌多项式展开方法，V型电热驱动器对称中心处的温度函数可以展开为二维多项式基函数的线性组合，即：

其中：aij为多项式的系数，p为混沌多项式展开截断阶数，系数aij的个数z：

H i（ζ）为根据变量ζ的特征分布得到的一维i阶正交基函数，其正交性质如下：

其中：<·>表示内积，权重函数f（ζ）为变量ζ的概率密度函数：

δij为克罗内克（Kronecker delta）函数。

在式（3）中，可将H i（ζ1）H j（ζ2）整体视为一个二维正交基函数，具有上述类似性质：

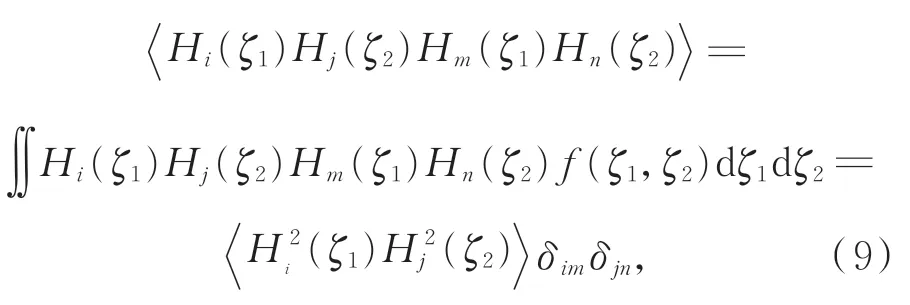
此时，权重函数f（ζ1，ζ2）为变量ζ1和ζ2的联合概率密度函数：

由于ζ1，ζ2均为标准正态分布，根据Askey［19］方案，基函数H（ζ1）H（ζ2）均为一维Hermite正交基函数。以下是5阶一维Herimite正交基函数：

4.2 系数求解

通过对上述建立的V型电热驱动器对称中心处的温度混沌展开模型的分析，系数aij为未知量。为对系数aij进行求解，温度展开方程（3）左右两端分别与各二维基函数进行加权求内积，得到：

根据式（8）二维正交基函数的性质，式（11）经化简得到：

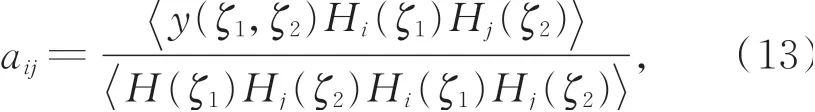
其中：分母的内积可直接积分得到，分子的内积可通过高斯数值积分法计算得到，具体如下：

其中：q为高斯积分阶数为q阶高斯积分的第k个积分点的计算可先对积分点做式（2）的反变换得到对应的电热驱动器宽度和电阻率值，然后进行有限元仿真得到V型电热驱动器对称中心处的温度；对应为第k，m个积分点处的权重之积。表2［20］给出3，5阶高斯积分的积分点和权重。

表2 3、5阶高斯积分的积分点和权重Tab.2 Third and fifth order gauss integration point and weight

5 有限元仿真及实验验证

由于在混沌多项式系数求解中，需通过有限元仿真计算得到各积分点处的V型电热驱动器对称中心处的温度。为保证非侵入式混沌多项展开模型的精确性，需对有限元仿真模型进行实验验证。这里选用20号微电热驱动器样品进行实验测试，具体参数如表3所示。根据20号微电热驱动器的参数，建立了相应的有限元模型。不同电压作用下，有限元计算位移和实验位移如图8所示。从图中可以看出：有限元模型位移计算结果与实验结果一致。因此，该有限元模型能够准确对V型电热驱动器进行模拟，基于该有限元模型得到的温度分布结果是可信的。

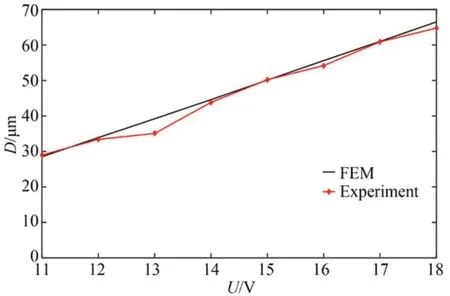
图8 不同电压作用下电热驱动器仿真与实验位移Fig.8 Displacement of the electro-thermal actuator by simulation and experiment under different voltages

表3 20号V型微电热驱动器样品参数Tab.3 Parameters of the 20th sample of the V-shaped electro-thermal actuator

6 结果验证与分析

为对混沌多项式展开方法得到的V型电热驱动器最高温度的概率密度分布结果验证，首先抽取不同样本数的微电热驱动器进行蒙特卡洛［21］模拟计算，其最高温度的均值如表4所示。随着抽样数的增加，最高温度的均值逐渐趋于收敛。从可信度和计算成本角度综合考虑，1000次抽样仿真的结果即可用于混沌多项式计算结果的验证。

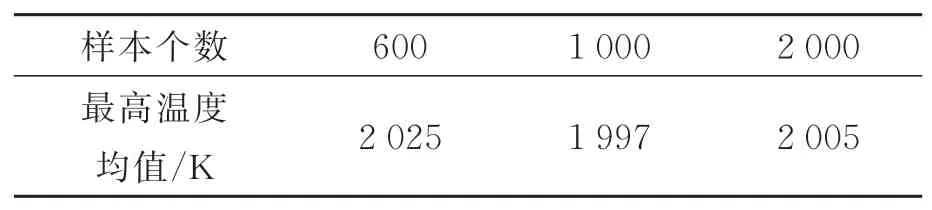
表4 不同抽样数下，V型电热驱动器最高温度的均值Tab.4 Mean value of the highest temperature on the Vshaped electro-thermal actuator with different numbers of samples

图10 18 V电压作用下电热驱动器最高温度概率密度分布Fig.10 Probability density distribution of the highest tem⁃perature on the electro-thermal actuator applied with 18 V

微电热驱动器最高温度的混沌展开多项式的阶数分别取3阶和5阶。高斯积分的阶数定为9阶，即每个变量维度上有9个高斯积分点。又由于混沌多项式中存在两个变量，因此共有81个积分点。在16 V，18 V加载电压下，分别由3阶、5阶混沌多项式和蒙特卡洛法计算得到的该加工批次的V型电热驱动器最高温度的概率密度分布如图9~10所示。从图中可以看出：分别由混沌多项式与蒙特卡洛法计算得到的最高温度概率密度分布曲线几乎完全重合，因此非侵入式混沌多项式展开方法可以准确对存在工艺误差的V型电热驱动器的最高温度进行不确定性量化。此外，使用蒙特卡洛法需进行1000组仿真，而采用混沌多项式展开方法只需对电热驱动器进行81组仿真。且随着混沌多项式中变量的增加，使用蒙特卡洛法抽取的样本数会呈指数型的增加，因此混沌多项式法有效地降低了计算成本。在16 V电压作用下，该加工批次的V型电热驱动器对称中心处的温度均值大约为1 600 K，温度分布范围大致在1 100～2 500 K；而18 V电压作用下的温度均值大约为2 000 K，温度分布范围大致在1 300～3 000 K。随着电压的增加，V型电热驱动器对称中心处的温度均值不断升高，温度分布范围也不断增大。在16 V和18 V电压作用下，5阶混沌多项式的温度概率密度曲线均要比3阶混沌多项式的曲线更为接近由蒙特卡洛法得到的曲线。因此，随着混沌多项式展开阶数的增加，V型电热驱动器最高温度分布的计算结果更为精确。

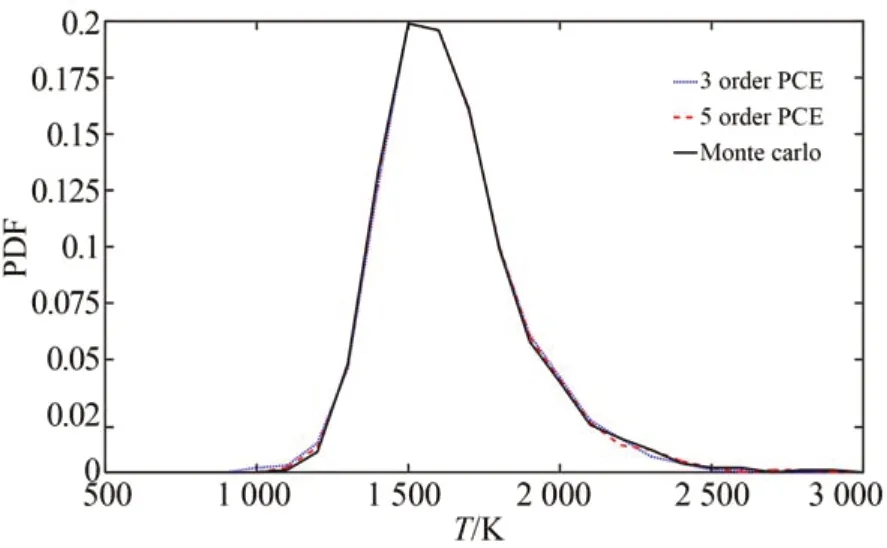
图9 16 V电压作用下电热驱动器最高温度概率密度分布Fig.9 Probability density distribution of the highest tem⁃perature on the electro-thermal actuator applied with 16 V

在16 V和18 V电压作用下，V型电热驱动器最高温度的累积密度曲线如图11所示。从图中可以看出：由于硅的熔点大约为1 700 K，因此在16 V电压作用下，该加工批次的V型电热驱动器的失效概率大约为41.4%；而在18电压作用下，该加工批次的V型电热驱动器的失效概率急剧增加达到了91.5%。不同电压下，V型电热驱动器的温度失效概率如图12所示。从图中可以看出：随着电压增大，温度失效概率逐渐增大；在16~17 V之间，V型电热驱动器的温度失效可能性急剧增加。

图11 16 V，18 V电压作用下，电热驱动器最高温度累积密度分布Fig.11 Cumulative density distribution of the highest temperature on the electro-thermal actuator ap⁃plied with 16 V and 18 V

图12 不同电压作用下，V型电热驱动器温度失效概率Fig.12 Failure probability of temperature of the Vshaped electro-thermal actuator with different voltages

7 结 论

本文对V型电热驱动器加工样品的宽度和电阻率进行了测量计算，发现其偏差满足正态分布。在ANSYS中建立的V型电热驱动器有限元模型的分析结果与实验结果一致。

基于非侵入式混沌多项式展开方法，根据宽度和电阻率误差分布，对V型电热驱动器最高温度进行不确定性量化分析，其分析结果与蒙特卡洛仿真结果一致，且结果精度与混沌多项式的精度有关。

通过对V型电热驱动器最高温度累积概率密度分析，并结合硅的熔点温度，可以得到：随着加载电压升高，驱动器温度失效概率也不断增大。当加载18 V电压时，驱动器的温度失效概率达到了91.5%。