核心约束空腹式型钢混凝土柱恢复力模型研究
2021-07-14周春恒陈宗平
周春恒, 陈宗平
(1.宁波大学 土木与环境工程学院,宁波 315211;2.广西大学 土木建筑工程学院,广西 南宁 530004;3.广西大学 工程防灾与结构安全教育部重点实验室,广西 南宁 530004)
型钢混凝土柱具有刚度大、承载力高、抗震性能好等优势,被广泛应用与高层建筑与重载厂房中[1-2]。其中,空腹式型钢混凝土柱比实腹式型钢混凝土柱具有更好的抗弯性能,且节点穿筋施工便捷,但是抗震性不及实腹式型钢混凝土柱[3-5]。针对这一情况,本文提出核心约束空腹式型钢混凝土(lattice steel reinforced core-confined concrete,LSRCC)柱,将螺旋箍筋配置于空腹式型钢混凝土柱的核心,增强其对混凝土的约束作用,提高延性和抗震性能[6];同时保持了空腹式型钢混凝土柱节点施工便捷的优势。
恢复力模型是弹塑性时程分析的基础,对结构的地震反应分析结果有着重要影响,国内外学者对型钢混凝土构件的恢复力模型进行了大量试验研究[7-10]。其中,周颖等[9]基于空腹式型钢混凝土柱的低周反复试验,建议了其骨架曲线及恢复力模型。石晶等[10]通过试验研究,提出空腹式型钢混凝土柱的退化三线型恢复力模型及其特征点的计算方法。然而,有别于传统空腹式型钢混凝土柱,LSRCC柱中螺旋箍筋能对核心混凝土提供额外的约束,且约束作用对混凝土柱的滞回特性产生极大的影响[11-12],李升才[13]在箍筋约束混凝土柱恢复力模型的研究中建议考虑配箍率的影响。因此,现有的空腹式型钢混凝土柱的恢复力模型难以适用于LSRCC柱。本文通过LSRCC柱的低周反复试验,分析了试件的滞回性能和恢复力特征,考虑型钢与螺旋箍筋的复合约束作用对其恢复力的影响,建立该新型柱的恢复力模型,为其弹塑性地震反应分析提供理论基础和依据。
1 试验概况
设计制作了8个1/2缩尺核心约束空腹式型钢混凝土柱试件,试件截面尺寸为250 mm×250 mm,高度为1 250 mm,剪跨比λ=3.4,试件几何尺寸及截面配钢如图1所示。在其他参数完全相同的情况下,试件LSRCC-1~LSRCC-3分别采用不同的轴压比,试件LSRCC-2、LSRCC-4及LSRCC-5分别采用不同的配箍率,试件LSRCC-2及LSRCC-6在总含钢率相同的条件下,采用不同的螺旋筋及缀板的配置形式,试件LSRCC-2、LSRCC-7及LSRCC-8分别采用了3种不同的截面配钢形式,具体参数见表1。各试件所采用混凝土的实测标准立方体抗压强度为46.85 MPa,弹性模量为3.19×104MPa,各类钢材力学性能见表2。

图1 试件尺寸及截面配钢

表1 试件设计参数

表2 钢材力学性能
试件采用悬臂柱式加载,轴压力由2 000 kN液压千斤顶通过反力架在柱端施加,水平反复荷载由500 kN电液伺服作动器施加。水平反复荷载采用混合控制分级加载,试件屈服前,以10 kN为荷载增量进行力控分级加载,每级循环1次;试件屈服后,以屈服位移的倍数为位移幅值进行位控加载,每级循环3次,直至承载力下降到峰值荷载的85%时结束,试验全过程通过FCS协调加载控制系统控制,并实时采集荷载和位移数据,获取滞回曲线。
2 滞回特性分析
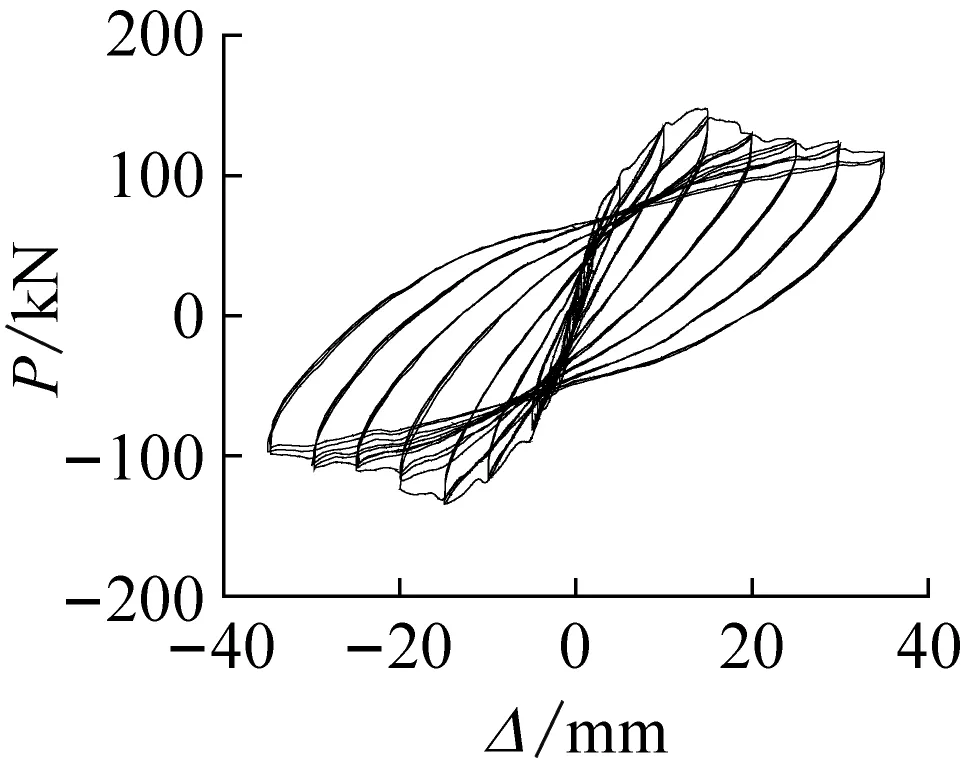
图2为各试件的滞回曲线,由图2可见,核心约束空腹式型钢混凝土柱的滞回曲线饱满,在试件达到峰值荷载前,同一位移幅值3次循环曲线基本重合,无明显的强度衰减和刚度退化;峰值荷载后,由于非约束区混凝土的剥落,随着位移幅值的增大强度衰减现象愈发显著,卸载刚度也存在明显的退化。
(a) LSRCC-1
轴压比对试件滞回特性的影响最大。当轴压比在在0.2~0.5时,随其增大,峰值荷载有所提高,轴压比为0.3和0.5时的峰值荷载较0.2时分别提高了27.0%和85.9%;但是滞回环的饱满程度、曲线的稳定性降低,强度衰减程度增大,峰点后的承载力的下降速度显著增大。
当螺旋箍筋间距在40~80 mm,型钢缀板间距在140~190 mm时,随着螺旋箍筋间距和型钢缀板间距的减小,滞回环趋于饱满,峰点后承载力的下降速度减小,曲线卸载刚度的退化速度降低。
三种截面类型试件的滞回曲线中,Ⅲ类截面试件(LSRCC-8)的复合约束作用最为显著,其水平峰值荷载、极限位移和滞回环所包围的面积均最大,而Ⅱ截面试件(LSRCC-7)由于螺旋箍筋的约束面积最小,其水平峰值荷载、极限位移和滞回环所包围的面积最小。Ⅲ类截面试件的峰值荷载和极限位移比Ⅱ截面试件分别高出31.7%31.4%。
3 骨架曲线模型的建立
3.1 骨架曲线模型的简化
为了得出准确的LSRCC柱骨架曲线特征,首先将试件骨架曲线进行归一化处理,如图3所示。
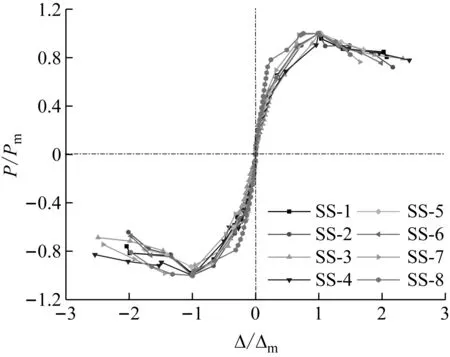
图3 归一化骨架曲线
由图3可见,各试件的骨架曲线近似符合存在屈服点、峰值点和极限点的三折线规律,故简化为图4所示的计算模型。具体简化规则为:
(1) 骨架曲线各特征点取值为相应的正向和负向值的平均值。
(2) 骨架曲线为包括弹性阶段、弹塑性阶段和下降阶段的三折线模型,考虑了屈服点、峰值点和破坏点三个特征点。
(3) 屈服点以前认为构件处于弹性变形阶段,其刚度按弹性刚度计算;屈服点到峰值点间认为构件处于弹塑性阶段,这一阶段试件刚度保持为相同值;峰值点之后为下降阶段,试件刚度同样保持为相同值。
3.2 骨架曲线模型特征参数的确定
三折线骨架曲线模型分为弹性阶段、弹塑性阶段和下降阶段,如图4所示。
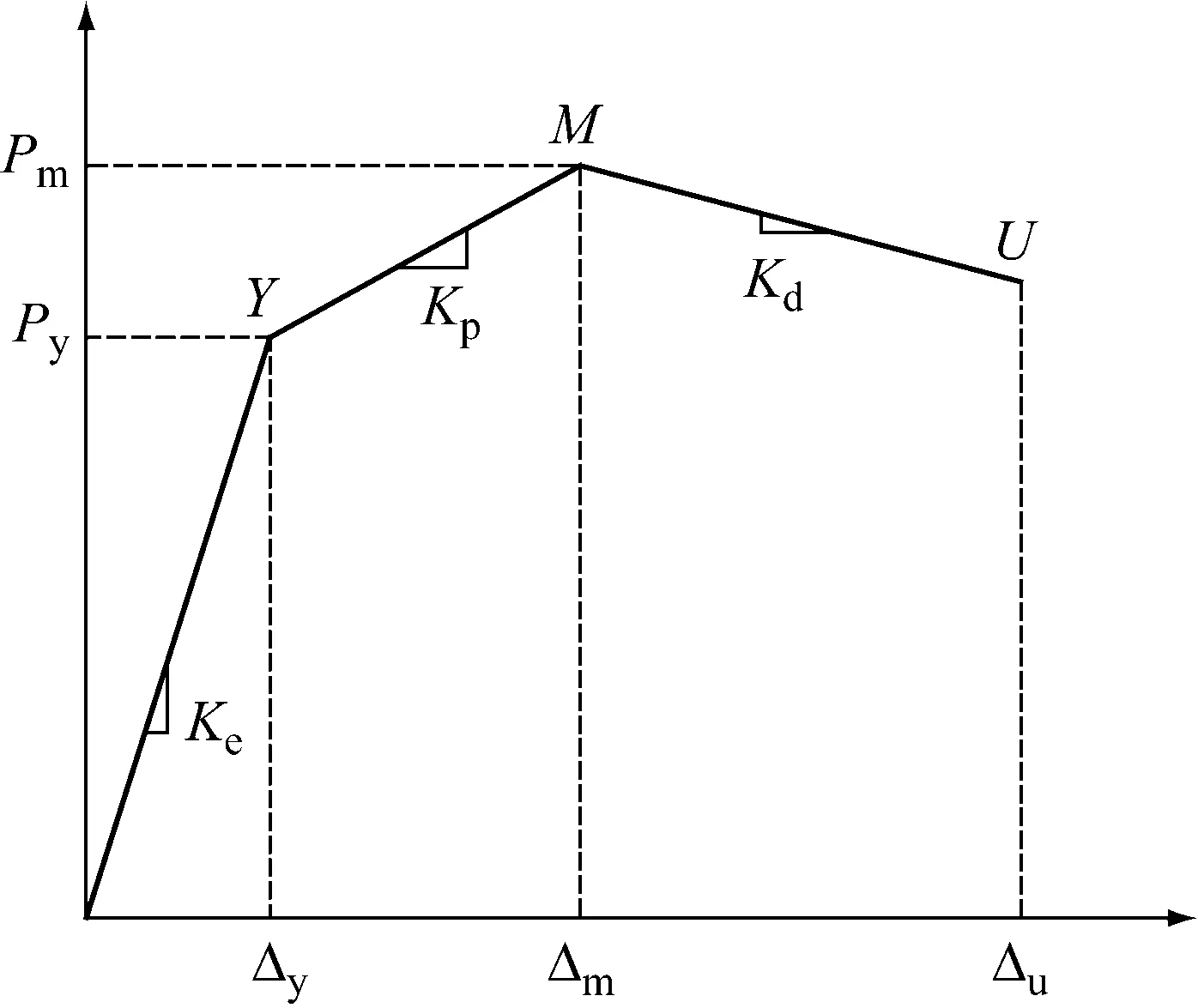
图4 骨架曲线模型
弹性阶段:虽有裂缝产生,但发展缓慢,斜率变化较小,简化为原点与屈服点(Py,Δy)相连的线段,需要确定的特征参数为屈服点荷载Py和弹性刚度Ke。
弹塑性阶段:表现为试件屈服后的强化特征,简化为屈服点(Py,Δy)与峰值点(Pm,Δm)相连的线段,需要确定的特征参数为峰值点荷载Pm和弹塑性刚度Kp。
下降阶段:承载力逐渐衰减,简化为峰值点(Pm,Δm)与破坏时极限点(Pu,Δu)相连的线段,需要确定的特征参数为极限点荷载Pu和软化刚度Kd。
(1) 弹性刚度Ke的确定
压弯剪共同作用下,LSRCC柱的弹性刚度应同时考虑弯曲变形和剪切变形的影响。型钢和螺旋箍筋的约束作用对弹性刚度的影响较小,故不考虑约束作用的影响,根据截面的弹性抗弯刚度、剪切刚度及试件的几何关系,由结构力学可计算LSRCC柱在弹性阶段的刚度
(1)
式中:H为柱高;EI为截面弹性抗弯刚度;GA为截面弹性抗剪刚度;k为截面剪切形状系数,矩形截面取1.2。
JGJ 138—2016《组合结构设计规范》给出了截面弹性抗弯刚度EI和弹性抗剪刚度的计算方法
EI=EcIc+EaIa
(2)
GA=GcAc+GaAa
(3)
根据材料力学,G与E存在相关性
(4)
式中:EcIc和GcAc分别为钢筋混凝土部分的截面抗弯刚度和抗剪刚度;EaIa和GaAa分别为型钢部分的截面抗弯刚度和抗剪刚度;ν为泊松比。
实际上混凝土在弹性阶段已产生了很多裂缝,因此,考虑开裂对试件抗弯刚度的影响,对式(2)进行修正,如下
EI=0.6EcIc+EaIa
(5)
(2) 峰值点荷载Pm的确定
所有试件均为压弯破坏,其峰值点荷载即为压弯极限承载力,根据试件的几何关系可得
Pm=M/H
(6)
式中:M为弯矩;H为柱高。
弯矩M参考文献[14]空腹式型钢混凝土柱偏压承载力的计算方法,根据式(7)、(8)确定
(7)
(8)
(3) 屈服点荷载Py的确定
文献[13-15]的研究结果均表明,SRC柱和箍筋约束混凝土柱的屈服点荷载与峰值点荷载均存在着一定的相关性。由图5可见,LSRCC柱的屈服点荷载与峰值点荷载与柱高相关,为近似线性关系。通过试验结果的线性回归可得

表3 峰值点荷载计算结果与试验结果对比

图5 屈服荷载与峰值荷载的关系
Py=0.71Pm-5.40/H
(9)
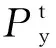

表4 屈服点荷载计算结果与试验结果对比
根据式(1)弹性刚度Ke的计算结果和屈服荷载Py的计算结果,可得到屈服位移Δy。
(4) 弹塑性刚度Kp的确定
弹塑性阶段是试件屈服后承载力依然上升的硬化过程,其刚度可用弹性刚度表示
Kp=αpKe
(10)
式中,αp为刚度硬化系数。
弹塑性刚度的确定需要考虑二阶效应、塑性铰长度、滑移变形等多因素的影响,使得理论计算复杂且结果存在离散性。另外,硬化过程可以看做是混凝土弹塑性发展的带裂缝工作阶段,而约束作用能限制裂缝的发展,对试件弹塑性刚度的大小有很大的影响。螺旋箍筋的约束作用主要与体积配箍率和约束范围的大小有关,型钢的约束作用主要与缀板体积配钢率和相应的约束范围有关。因此,本文通过试验结果的线性回归确定刚度硬化系数αp,并以螺旋箍筋配箍率体积配箍率、螺旋箍筋有效约束系数、缀板体积配钢率和型钢有效约束系数为表征,以体现型钢与螺旋箍筋的复合约束作用对螺旋筋约束增强空腹式型钢混凝土柱弹塑性刚度的影响
(11)
式中:n为轴压比;ρv为螺旋箍筋体积配箍率;ρvb为缀板体积配钢率;ηs为螺旋箍筋约束系数,取螺旋箍筋有效约束面积与试件总的截面积之比;ηb为型钢有效约束系数,取型钢骨架的约束面积与试件总截面之比;r为截面类型系数,由于型钢包裹在混凝土外部,Ⅲ类截面试件在弹塑性阶段的裂缝极少,达到峰点前,混凝土未发生剥落,达到峰点后混凝土的破坏情况也远小于Ⅰ类和Ⅱ类截面试件,通过图3骨架曲线的对比也可知,二者弹塑性刚度有很大的差异,所以Ⅰ类和Ⅱ类截面r取1.0,Ⅲ类截面r取0.66。
根据弹塑性刚度Kp、峰值点荷载Pm、屈服点荷载Py和屈服点位移Δy,通过下式可得到峰值点位移
(12)
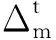

表5 峰值点位移计算结果与试验结果对比
(5) 软化刚度Kd的确定
峰值点后,试件的承载力开始衰减,刚度出现软化。这一阶段的刚度也可以通过弹性刚度表示
Kd=αdKe
(13)
式中,αd为刚度软化系数。
以螺旋箍筋配箍率体积配箍率、螺旋箍筋有效约束系数、缀板体积配钢率和型钢有效约束系数来体现型钢与螺旋箍筋的复合约束作用对LSRCC柱软化刚度的影响,通过试验结果的线性回归确定刚度软化系数αd
(14)
与式(11)相同,Ⅰ类和Ⅱ类截面r取1.0,Ⅲ类截面r取0.66。
(6) 极限点荷载Pu的确定
根据本文对屈服点荷载的定义,取下降段0.85Pm所对应的荷载值,故
Pu=0.85Pm
(15)
由下降段软化刚度Kd、峰值点荷载Pm、极限点荷载Pu和峰值点点位移Δm,通过下式可得到极限点位移
(16)

表6 极限点位移计算结果与试验结果对比
3.3 试验验证
通过上述方法确定各特征参数后,即可获得LSRCC柱的骨架曲线模型。利用骨架曲线模型计算各试件的骨架曲线,并与试验实测的骨架曲线进行对比,如图6所示。由图可见,计算骨架曲线与试验实测骨架曲线有较高的吻合度,说明所建议的LSRCC柱骨架曲线较好的反映了各试件的荷载-位移关系,并且能够体现出复合约束作用、轴压比和截面类型的影响。
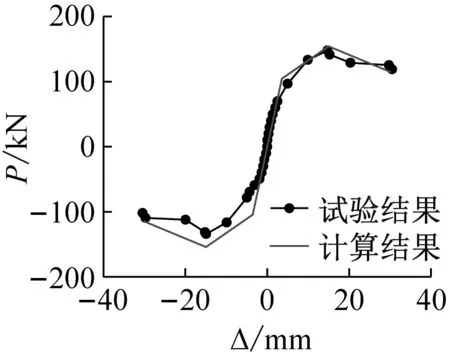
(a) LSRCC-1
4 恢复力模型的建立
4.1 滞回规则的确定
通过对LSRCC柱滞回特性的分析,在已建立的骨架曲线模型的基础上,确定其恢复力模型的滞回规则,如图7所示,具体如下:
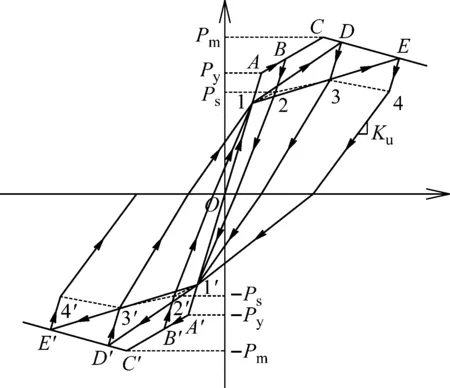
图7 螺旋筋约束增强空腹式型钢混凝土柱的恢复力模型
(1) 根据实测滞回曲线特性,当试件加载至屈服后,刚开始卸载时,卸载刚度与弹性刚度,当到达某一点时(2、2′、3、3′、4、4′),由于混凝土的开裂剥落,卸载刚度出现软化,不再与弹性刚度相同,本文定义这一点为软化点,弱化点荷载Ps按下式计算
Ps=0.75Puu
(17)
式中:Ps为软化点荷载;Puu为卸载点荷载。
(2) 反向再加载时,所有曲线均经过弹性段上的某一点(1、1′),本文定义为再加载指向点;再加载指向点荷载和位移分别取0.75Py和0.75Δy。
(3) 由于强度衰减程度与众多因素有关,计算复杂[16],故本文建议的恢复力模型不考虑试件的强度衰减。
(4) 试件屈服前,加载和卸载路径沿着骨架曲线模型弹性阶段进行,加卸载刚度均与弹性刚度一致。正向加卸载时,沿着OA线段;反向加卸载时,沿着OA′线段。
(5) 试件屈服后达到峰值荷载前,加载路径沿着骨架曲线模型弹塑性阶段进行,即AC线段。加载至位移幅值点(B点)时开始卸载,初始卸载按弹性刚度进行,当卸载至软化点(2点)时,试件产生软化,而后按卸载刚度Ku卸载,直至荷载降为0。反向再加载时,首先指向再加载指向点(1′点),之后沿着反向骨架曲线模型加载,首先加载至屈服点,即1′A′或1A线段,而后沿着AC′线段进行。反向卸载规则与正向相同。在这一阶段,一个完整的滞回路径为:O-A-B-2-1′-A′-B′-2′-1。
(6) 试件达到峰值点后,加载路径由再加载指向点(1点)指向位移幅值在骨架曲线模型下降阶段上的点(D点)。加载至D点后开始卸载,与前一阶段一致,初始卸载按弹性刚度进行,当卸载至软化点(3点)后,按卸载刚度Ku卸载,直至荷载降为0。反向再加载时,首先指向再加载指向点(1′点),之后由1′点指向位移幅值在反向骨架曲线模型下降阶段上的点(D′点),沿着1′D′线段再加载。之后的反向卸载规则与正向相同。在这一阶段,一个完整的滞回路径为:1-D-3-1′-D′-3′-1。而后直至试件破坏的滞回规则均与上述相同,根据位移幅值的确定滞回路径。
4.2 卸载刚度的确定
由试件的实测滞回曲线可知,随着位移幅值的增加,卸载刚度Ku不断降低。这是由于试件的裂缝随着位移的增大而逐渐增大,混凝土剥落愈发严重,钢材的不可恢复变形也逐渐增加。型钢与螺旋箍筋的约束作用能有效的裂缝的发展和混凝土的剥落,必然会对螺旋筋约束增强空腹式型钢混凝土柱的卸载刚度Ku有所影响。
将卸载刚度Ku通过弹性刚度Ke表示
Ku=αuKe
(18)
式中,αu为卸载刚度系数。
通过螺旋箍筋配箍率体积配箍率、螺旋箍筋有效约束系数、缀板体积配钢率和型钢有效约束系数来考虑型钢与螺旋箍筋的复合约束作用对螺旋筋约束增强空腹式型钢混凝土柱卸载刚度的影响。经过回归分析,建议螺旋筋约束增强空腹式型钢混凝土柱恢复力模型的卸载刚度系数为
(19)
式中,Δuu为卸载点位移。
4.3 试验验证
利用上述建议的恢复力模型对螺旋筋增强空腹式型钢混凝土各试件的滞回曲线进行计算,计算结果与试验实测结果的对比如图8所示。由图可见,各试件的计算结果与试验结果吻合较好。并且该模型能很好的反映型钢与螺旋箍筋复合约束作用的影响。
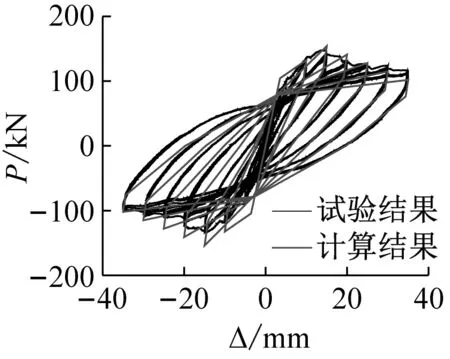
(a) LSRCC-1
5 结 论
本文在对8个核心约束空腹式型钢混凝土柱试件低周反复试验的基础上,针对其滞回特性,建立了考虑型钢与螺旋箍筋复合约束作用的核心约束空腹式型钢混凝土柱的恢复力模型。结论如下:
(1) 核心约束空腹式型钢混凝土柱的滞回曲线饱满,强度衰减和加、卸载刚度退化等滞回特性主要受轴压比、截面类型、螺旋箍箍筋配箍率和型钢间接配钢率的影响。
(2) 所建议的骨架曲线模型采用三折线模型,在模型特征参数的计算中考虑了复合约束作用的影响,量化了型钢与螺旋箍筋的约束效应;骨架曲线模型与实测骨架曲线吻合较好。
(3) 所建议的恢复力模型考虑了复合约束作用的卸载刚度Ku,恢复力模型与实测滞回曲线吻合较好,能较好的反应不同轴压比和复合约束效应对核心约束空腹式型钢混凝土柱滞回特性的影响。
