铁路桥上直立式声屏障车致振动研究

2021-07-14李小珍雷康宁龚振华

振动与冲击 2021年13期

李小珍，雷康宁，龚振华，毕然，胡喆，徐鸿，郑净

(1.西南交通大学土木工程学院，成都 610031； 2.中铁第四勘察设计院集团有限公司，武汉 430063; 3.中铁二院工程集团有限责任公司，成都 610031)

随着轨道交通的迅猛发展，列车过桥时所诱发的桥梁振动与噪声问题愈发突出，人们对噪声的容忍度也随着生活质量的改善而越来越低。当列车时速低于300 km，轮轨噪声在总噪声中占主导地位[1]，声屏障常作为一种降低轮轨噪声的有效措施被广泛采用。

声屏障结构的形式多种多样，为了避免与铁路附属构筑物相互干扰，影响安全限界，轨道交通中仍多采用直立式声屏障。现有研究多针对声屏障声学特性进行，而随着车速的增加，轮轨激励作用增强，列车过桥时引起桥梁及其上声屏障振动加剧。此时声屏障和桥梁将作为振源向四周辐射噪声，从而间接削弱了声屏障的降噪效果[2]。因此开展桥梁及其上声屏障结构的振动规律研究，对进一步提出减振措施和降低桥梁-声屏障辐射噪声具有至关重要的意义。

为了对声屏障结构的动力特性进行研究，Rocchi等[3]开展了现场试验，测试了轨道附近的流场和作用于声屏障、道床板上的列车风压，并对不同列车的气动特性进行了对比分析。Xiong等[4]通过现场试验的方法，测试了CRH380A运行时，直立式声屏障表面的脉动风压分布。何佳骏等[5]通过CFD对列车通过全封闭声屏障时形成压力波进行研究，探究了压力波在横、纵向分布的特点及衰减特性。龙丽平等[6-7]基于流体计算软件CFX，探究了列车通过声屏障过程中空气脉动力的分布规律。吕坚品等[8]探讨了脉动力的不同输入方式对不同跨度的铁路桥上声屏障动力响应的影响规律。陈向东等[9]基于ALE方法建立了列车-声屏障三维数值模型，分析了脉动力分布特性和时程特性的各项影响因素。

近年来，国内学者开始关注桥上声屏障的车致振动问题。李小珍等[10]对桥梁-封闭式声屏障的振动开展了现场测试，得出声屏障的振动大于箱梁振动，且呈现宽频特性的结论。罗云柯等[11]对某高速铁路箱梁和半封闭声屏障开展了现场测试，建立数值模型进行了计算分析，得到了桥上声屏障振动的传递路径和衰减规律，并提出了相应的减振措施。谢伟平等[12-13]通过对某轨道交通高架桥上半封闭式声屏障进行现场测试，分析了其动力特性及振动的传播规律，得到曲线段半封闭式声屏障的车致振动响应大于直线段的结论。

总体来说，已有的声屏障动力问题研究中，更多的是围绕列车脉动风压作用下声屏障的振动特性进行，关于声屏障车致振动的研究较少。同时，鲜有文献对直立式声屏障车致振动进行研究。由于直立式声屏障应用更为广泛，与封闭式声屏障相比，受列车脉动风压作用影响相对较小，且其基础通常安装于箱梁的翼缘板外边缘，高速列车的轮轨动力作用效应不容忽视。本文基于车-线-桥耦合振动分析理论，采用数值模拟与现场试验相结合的方法对桥上直立式声屏障车致振动特性进行研究，提出相应的减振措施，以期能够为今后直立式声屏障减振优化设计提供参考。

1 试验概述

现场试验以某双线铁路上安装有直立式声屏障的32 m混凝土简支箱梁为工程背景，如图1所示。混凝土简支箱梁梁长32.6 m，计算跨度31.5 m，采用单箱单室截面形式，桥面宽12.0 m，梁体中心线处高2.784 m，顶板厚0.34 m，腹板厚0.36 m，底板宽5 m、厚0.28 m。梁体采用C50混凝土，轨道中心线之间的距离为4.60 m，设计速度为200 km/h，二期恒载取174 kN/m，设计活载为ZC活载。

图1 铁路桥上直立式声屏障

桥上采用有砟轨道，其结构由钢轨、扣件、钢筋混凝土轨枕以及道床结构构成，采用标准轨距1 435 mm，轨枕间距为60 cm，钢轨采用CHN60型，扣件竖向刚度为60 MN/m。

桥上直立式声屏障高度为5.0 m，采用H型钢立柱，尺寸为250 mm×250 mm×9 mm×14 mm，顺桥向以2 m等间距布置。隔声单元板采用铝合金复合吸声板，厚度为140 mm，高度为0.5 m，沿高度方向共布置10块。单元板与H型钢立柱之间及上、下单元板间垫有三元乙丙橡胶垫层。

图2给出了箱梁以及声屏障立柱上的振动测点位置，图3给出了现场试验的传感器布置照片，所有测点均布置在跨中断面。其中，测点V1位于相邻扣件之间的钢轨下方，测点V2位于箱梁顶板中心，测点V3和V4分别布置在与声屏障第1和第5块单元板顶端等高处，至立柱底部距离分别为0.5 m和2.5 m。各测点采用CA-YD-189型压电式加速度传感器，使用东方振动和噪声技术研究所制造的INV3060S型24位智能采集仪进行实验数据采集，采样频率为1 024 kHz。

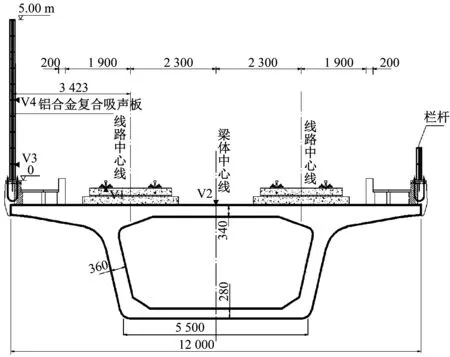
图2 振动测点布置示意图(mm)

图3 现场测试传感器布置

2 试验结果分析

由文献[14]可知，箱梁-声屏障辐射的结构噪声主要来源于声屏障的水平局部振动和箱梁板件面外振动。故对于箱梁选择测试顶板垂向加速度，声屏障立柱测试横向加速度。现场测试时，列车运行速度约为80 km/h，为避免测试结果具有偶然性，现场采集了多组数据。选取通过车型为CRH1A的三组数据，从时域和频域两个角度分析钢轨、箱梁以及声屏障立柱各部位振动的分布情况。

2.1 时域分析

列车通过时，钢轨及箱梁顶板测点振动加速度时程曲线如图4所示。图4中，加速度时程包含了列车从上桥导致桥梁振动到离开后振动衰减的全过程。

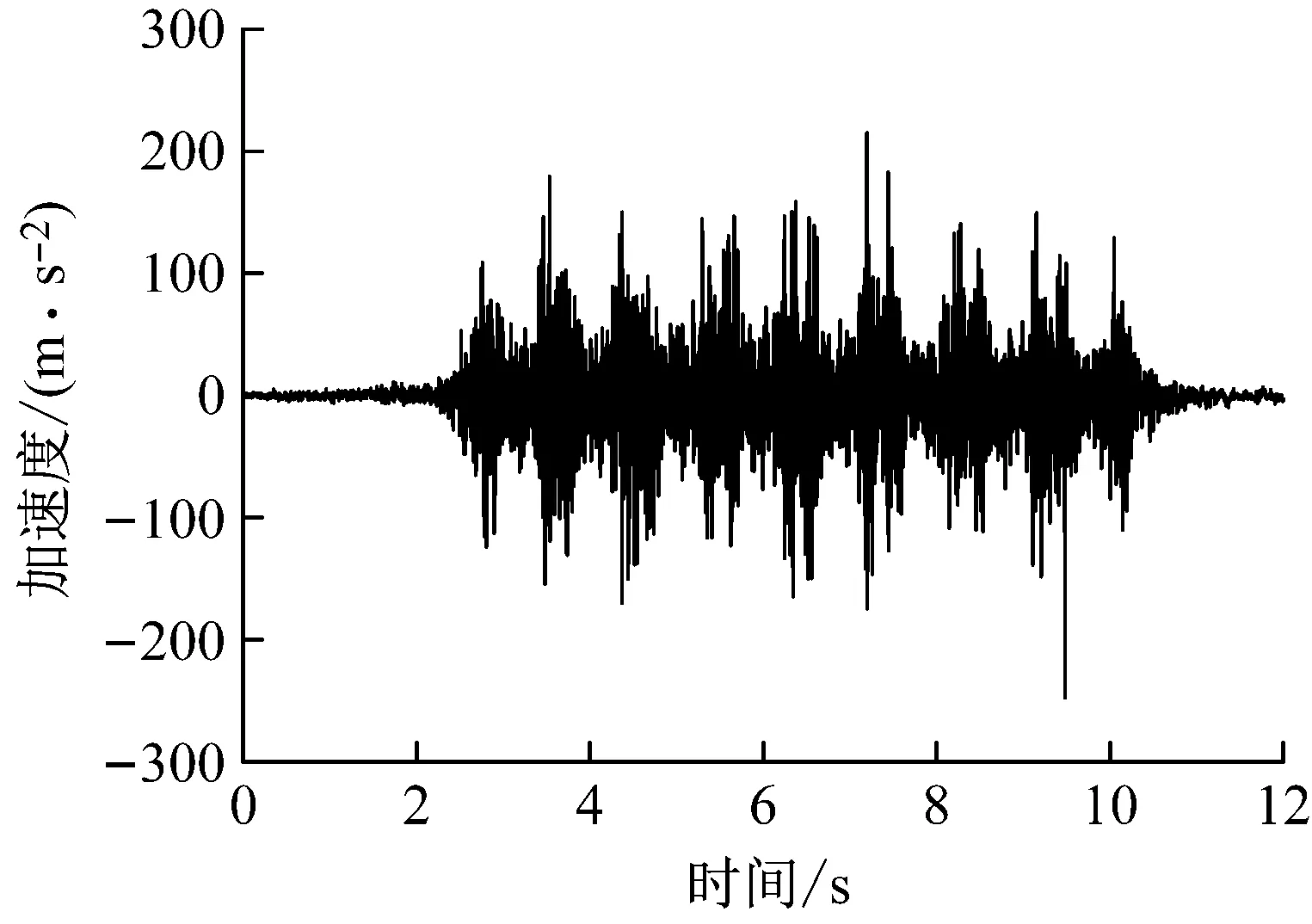
(a) V1(钢轨)

由图4可知，列车经过桥上时，钢轨和箱梁顶板振动加速度时程具有明显的峰值和周期性变化，可以清晰地识别出列车的编组形式(8节，总长200 m)。可以看出，列车通过测试断面的持续时间约为9 s，行车速度与实测80 km/h相近。从加速度大小来看，钢轨的振动加速度有效值为16.89 m/s2，瞬时峰值超过250 m/s2；经过扣件、轨枕、道砟的减振效应传递至箱梁顶板时，振动能量大大衰减，振动加速度有效值降为0.15 m/s2，瞬时峰值接近2.00 m/s2。

列车通过时，跨中截面声屏障立柱底部和中部测点振动加速度时程曲线如图5所示。

(a) V3(立柱底部)

由图5可知，声屏障立柱振动时程曲线持续时间与箱梁接近，声屏障立柱底部振动较为稳定，加速度幅值约为1.50 m/s2，瞬时峰值接近3.00 m/s2；与立柱底部相比，中部振动具有明显的峰值和周期性变化，瞬时峰值接近3.00 m/s2。

立柱底部和中部之间存在差异。首先，直立式声屏障立柱上部无约束，而底部具有较强约束。其次，立柱底部在箱梁翼板附近，主要随翼板共同发生竖向和横向振动，因此横向振动加速度时程曲线无明显的周期性变化。而立柱中上部横向振动则主要由箱梁受偏载和横向轮轨力作用时发生的扭转以及竖向变形控制，因此与桥梁顶板竖向振动特性相近，即曲线具有明显的峰值和周期性变化。

2.2 频域分析

为分析箱梁-声屏障结构振动水平在频率上的分布特性，采用振动加速度级VAL对振动水平进行评价。由于轮轨力频率分布范围较大，本文采用三分之一倍频程对各处的振动响应进行分析，采用振动加速度总振级对各测点振动强弱进行评价，计算方法如下

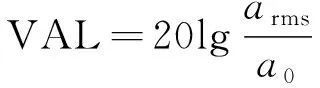
(1)

式中：VAL为振动加速度级(dB)；arms为振动加速度有效值(m/s2)；a0为基准加速度，取a0=10-6m/s2。

图6给出了钢轨、箱梁顶板中心以及声屏障立柱底部和中部测点三次实测振动加速度级频谱曲线及其总振级柱状图。

(a) V1(钢轨)

从图6中可以看出，各测点在三次测试中得到的频谱曲线特性相同，具有很高的重合性，表明现场测试结果可信度较高。通过分析各图，可得到以下结论：

(1) 钢轨振动加速度级在中低频范围内随频率的增大而增大，在1 250 Hz处，钢轨振动加速度级达到峰值147.98 dB，随后随频率增大而减小；

(2) 箱梁顶板中心的振动加速度级峰值为107.88 dB，出现在中心频率200 Hz附近，总振级约为111 dB；

(3) 声屏障立柱底部的振动加速度级峰值频率为50 Hz，在低于50 Hz频段，振级随频率增大而增大，50～160 Hz频段内随频率增加下降明显，在250 Hz处出现次峰值，随后随频率增加总体呈现出下降趋势；

(4) 声屏障立柱中部测点的振动加速度级优势频段为50～500 Hz，峰值频率为50 Hz，低于50 Hz频段与立柱底部保持相似特性，振级随频率增加而增加，50 Hz频段以后总体随频率增加而下降，在200～500 Hz频段内具有较大的波动；

(5) 振动加速度总振级在声屏障立柱底部高于立柱中部，且均高于箱梁顶板，其原因在于立柱安装在箱梁翼缘边缘处，列车通过时箱梁翼缘鞭梢效应突出。

3 数值分析

3.1 轮轨相互作用力的求解

本文通过建立如图7所示的轨道结构模型求解轮轨力，从下到上依次模拟桥梁、道砟、轨枕及钢轨，模型仅考虑垂向振动。车辆模型仅考虑转向架、一系悬挂以及轮对，考虑相邻车厢间距离较近的4个轮对之间的相互影响，车辆轴距和前后车辆相邻轮对间距分别为L1和L2。钢轨、轨枕、道砟和桥梁之间均采用弹簧-阻尼进行连接，钢轨视为无限长Timoshenko梁，轨枕简化为Euler梁，道砟简化为离散质量块，桥梁视为刚性基础。

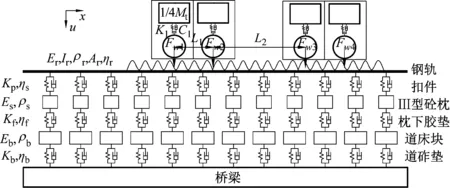
图7 轮轨相互作用模型

轮轨力计算时采用移动不平顺模型，由动柔度法计算动态轮轨力公式如下

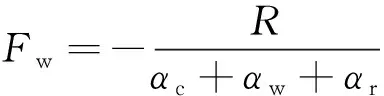
(2)

式中:R为轨道组合不平顺;α为动柔度，其下标c、w和r分别表示轮轨接触、车轮和钢轨动柔度。轮轨接触柔度可表示为：

αc=1/Kc

(3)

式中,Kc为线性轮轨接触刚度。

本文采用叠加法求解钢轨的动柔度，多车轮间的相互作用采用主动轮与被动轮的方法考虑。依次以每个车轮作为主动轮，求得该车轮作用处的钢轨动柔度αri、扣件力及枕下胶垫和道砟垫支持力，然后代入式 (2) 并考虑轨道不平顺的时间滞后效应，即可求得多个车轮单独作用下的轮轨力，详细求解过程见文献[15-17]。

本文动态轮轨力计算模型参数按表1和表2取值，列车车型为CRH1A，轨道不平顺按ISO 3095(2013)取值。

表1 车辆计算参数

表2 有砟轨道参数

采用以上参数，利用Matlab自编程序求解，得到轮轨相互作用力频谱图如图8所示。

图8 轮轨相互作用力

3.2 箱梁-声屏障耦合模型建立

声屏障结构作为桥上附属设施，可以统一作为车桥系统中的“桥梁子系统”进行研究，采用有限元软件ANSYS建立桥梁-声屏障耦合振动分析模型。各板件的局部振动对结构的动力特性影响较大，为获取结构的中高频振动响应，箱梁和声屏障立柱均采用板单元shell63建立。混凝土箱梁划分为顶板、翼缘、腹板、底板四部分，声屏障立柱由两块翼板和腹板构成。轨道结构以及桥上其他附属设施的质量，以174 kN/m的二期恒载添加到箱梁顶板中加以考虑，忽略这些结构对箱梁及声屏障立柱振动产生的其他影响。

声屏障立柱底部与箱梁翼缘板间视为固接，根据声屏障隔声单元板之间的连接具有足够弹性的特点，忽略其对声屏障结构的刚度贡献，仅将其作为附加质量添加到声屏障立柱上。建立的箱梁-声屏障耦合振动分析模型及典型振型如图9所示。由图可知，箱梁一阶竖弯频率为3.87 Hz，声屏障立柱一阶横弯频率为8.79 Hz。

(a) 模型

3.3 模型验证

由于本次测试路段行车速度较低，直立式声屏障受到的列车脉动风压可以忽略，且根据文献[18-20] 可知，高速列车脉动风荷载集中在2～4 Hz的低频段，故本文研究声屏障10～1 000 Hz频段振动时，可以忽略脉动风所产生的振动效应，本次现场测试结果可以直接作为车致振动响应进行模型验证，而不必考虑其是否包含了风致振动成分。图10给出了箱梁顶板中心(V2)和声屏障立柱中部(V4)两个测点处仿真值与实测值的三分之一倍频程曲线，其中实测值取三次试验值的平均值，计算频率范围为10～1 000 Hz。

(a) 箱梁顶板中心(V2)

由图10可知，箱梁顶板中心和声屏障立柱中部计算与实测得到的频谱曲线变化规律基本一致。V2和V4测点的振动加速度总振级计算值分别为107.8 dB和110.9 dB，均与实测值110.9 dB和114.3 dB相差较小，即通过本文建立的车-线-桥-声屏障耦合振动分析模型具有较高的可靠性，可进一步用于桥梁-声屏障振动特性研究。

同时，由上述结果可知，不论是箱梁顶板中心测点还是声屏障立柱中部测点，其总振级的计算值均小于实测值，这是由于计算模型中仅考虑了竖向轮轨作用力，忽视了轮轨横向力的影响，而实际上箱梁在横向轮轨力的作用下会发生扭转变形，使得箱梁顶板中心竖向振动和声屏障立柱横向振动进一步增大。

4 振动结果分析

利用3.2节建立的桥梁-声屏障耦合振动分析模型，以列车运行时轮轨相互作用力作为激励力进行谐响应分析，得到铁路直立式声屏障车致振动响应的分布规律，探讨了行车速度对其振动的影响，并提出了一种减振措施以供设计参考。

4.1 振动分布规律

为分析不同断面处声屏障立柱振动的分布规律，选取1/8断面、1/4断面和跨中断面，分别给出声屏障立柱底部、中部和顶部三个部位振动加速度总振级柱状图，如图11所示，计算车速为200 km/h。

图11 声屏障立柱振动加速度总振级分布

由图11可知，同一高度处，声屏障立柱的振动加速度总振级在跨中截面处最大，沿箱梁纵向呈现出从端部向跨中截面逐渐增大的趋势，主要原因为箱梁跨中断面受支座约束较弱，振动更为剧烈。由此可以看出，在进行简支梁桥上声屏障振动分析时，应重点关注跨中断面的振动水平。从1/8断面到跨中断面，立柱底部、中部和顶部的总振级分别增加2.2 dB、13.4 dB和12.0 dB，表明立柱底部的振动受断面位置的影响很小，而中部所受影响最为明显。

此外，同一断面处，声屏障立柱的振动沿高度方向具有相似的分布规律，其在中部小于底部，这与现场试验的结果一致。立柱底部距箱梁翼缘较近，受翼缘鞭梢效应的影响最为剧烈，而立柱顶部无约束，处于自由状态，故振动更为剧烈。但这种在不同高度上的差异由梁端向跨中逐渐缩小，至跨中时，各点振动水平较为接近。

4.2 行车速度

图12给出了在不同车速的列车通过桥梁时，箱梁顶板中心和声屏障立柱不同部位的振动加速度总振级柱状图，计算车速选择120 km/h、150 km/h、180 km/h、200 km/h。

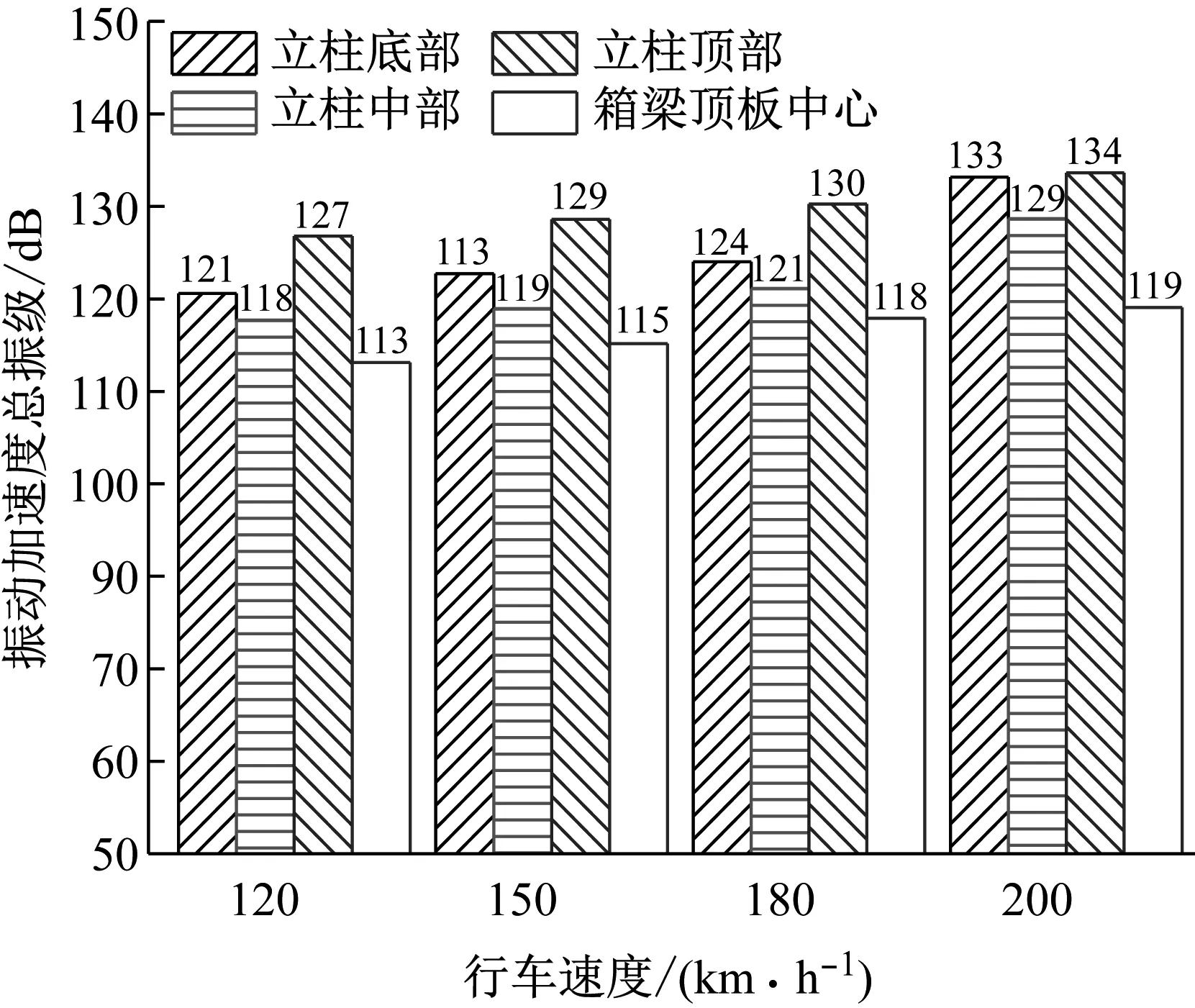
图12 各处总振级随车速变化

可以看出，相同速度下，声屏障立柱的振动较箱梁顶板更剧烈，而其振动加速度总振级均随车速的增大而不断增大。相对于声屏障立柱而言，箱梁顶板的振动受车速影响较为平缓，表现为车速每增加30 km/h，总振级约增大2 dB。而声屏障立柱各点，在车速低于180 km/h时，表现出与箱梁顶板相似的变化特性，当车速达到200 km/h时，声屏障立柱的振动显著加剧，在底部和中部尤为明显。原因在于，高速行车时列车轮轨力的频谱特性发生了变化，而声屏障立柱更易受轮轨力变化的影响。