高转速硬涂层阻尼薄壁圆柱壳的行波共振特性研究
2021-07-14杨志宏于晓光
王 宇, 夏 鑫, 杨志宏, 于晓光
(辽宁科技大学 机械工程与自动化学院,辽宁 鞍山 114051)
薄壁圆柱壳类构件在航空航天和舰船等叶轮旋转机械中应用广泛,例如:航空发动机的鼓筒和高压轴等典型的薄壁圆柱壳构件,低阶振动时通常具有轴向半波数为1的特征。随着燃气轮机等动力装备的升级换代,在外部复杂服役工况条件下,此类构件的振动问题越来越突出,容易产生共振、失稳和局部疲劳失效等问题[1-3]。采用硬涂层阻尼技术提高结构的动力学特性,近年来得到了学者的广泛关注,在现有薄壁壳体构件的硬涂层技术中,采用特殊的金属基硬涂层阻尼材料,研究结构的动力学特性,进而可以提高构件使用寿命的作用,有效的避免振动疲劳等问题。因此,针对高转速硬涂层阻尼薄壁圆柱壳构件的共振特性进行研究,具有一定的指导意义和工程应用价值。
针对薄壁壳体结构的振动问题,近几年得到了相关科技工作者的广泛重视,取得了可观的研究成果[4-10]。对于具有硬涂层阻尼技术薄壁结构的振动研究,也开始引起了学者们的高度重视,具有代表性的研究成果如下:杜广煜等[11-12]采用电弧离子镀法在不锈钢基片上沉积制备和研究了NiCrAlY涂层的化学和物理属性,结果表明NiCrAlY阻尼涂层能明显地提高基底的性能。Ren等[13]通过有限元法研究了硬涂层阻尼薄壁圆柱壳的固有特性和硬涂层参数变化对构件的影响。Li等[14]通过实验研究了悬臂边界条件下硬涂层对薄壁圆柱壳的影响,结果表明NiCrAlCoY+YSZ硬涂层能引起固有频率的轻微变化,在低阶/低频时阻尼效应更明显。Chen等[15]采用能量法和Rayleigh-Ritz法,对带有NiCrAlY硬涂层阻尼叶片的叶盘结构进行了振动分析,结果表明硬涂层有明显的阻尼作用,而整体叶盘只产生了轻微的频率变化。Yang等[16]基于Voigt-Reuss等效原理和Lindstedt-Poincaré扰动方法求解了带有NiCrAlY硬涂层薄板的固有特性,并对其非线性振动特性进行了行为研究。Sun等[17]采用瑞利-里兹法分析了固支-自由边界条件下NiCrAlCoY+YSZ硬涂层薄壁圆柱壳构件的自由振动特性。Song等[18]基于Voigt方法求解了悬臂时旋转薄壁壳体结构的高阶振动特性。张月等[19]采用有限元方法研究了固支-自由边界条件下考虑应变依赖性的NiCrAlCoY+YSZ硬涂层圆柱壳的固有特性。王宇等[20]针对三种边界约束条件下旋转态光滑薄壁圆柱壳的共振问题进行了探讨。综上所述,在高速旋转时,目前对于以NiCrAlY和NiCrAlCoY+YSZ阻尼材料为代表的硬涂层薄壁圆柱壳构件,其共振特性尚缺少相应的研究。
因此,针对高速旋转硬涂层薄壁圆柱壳构件,在固支-自由、简支-简支和固支-固支三种典型边界条件下,基于Love薄壳理论、Viogt-Reuss原理和传递矩阵法对构件的振动特性进行求解,并与文献中的计算结果进行比较,分析两种具有代表性硬涂层材料薄壁圆柱壳构件的模态特性与倍频激振作用下的共振特性,为硬涂层薄壁壳体类复合结构的振动设计研究提供理论支撑。
1 旋转硬涂层薄壁圆柱壳的行波共振特性
1.1 旋转态硬涂层薄壁圆柱壳模型
在柱坐标系Oxθz中,图1为旋转态硬涂层阻尼薄壁圆柱壳的模型,O为模型端面上的圆心,以角速度Ω绕x轴旋转,基体和硬涂层的长度均为L,基体的半径和厚度表示为R1和H1,硬涂层的半径和厚度表示为R2和H2,uj、vj和wj(j=1,2)分别表示基体和硬涂层在x轴、y轴和z轴方向上的振动位移,硬涂层薄壁圆柱壳沿x轴方向分成n0个子段,每个区段的长度分别为L1,L2,…,Li,…Ln0。
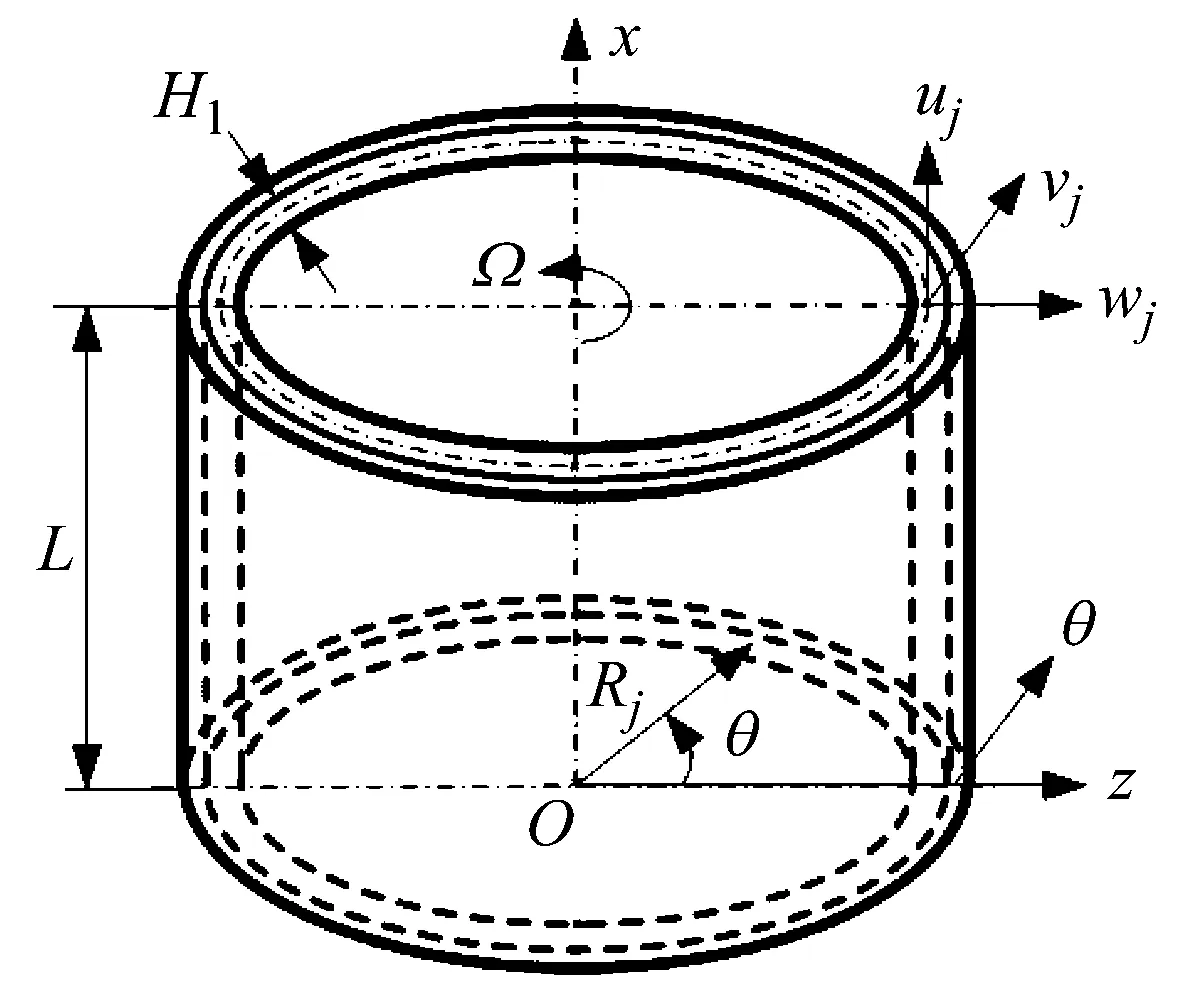
(a) 硬涂层薄壁圆柱壳构件
1.2 硬涂层薄壁圆柱壳的行波共振特性求解
根据复合结构的Viogt-Reuss等效原理,把硬涂层薄壁圆柱壳进行等效处理,等效材料的弹性模量、泊松比、密度和剪切模量用硬涂层材料和基体材料的弹性模量、泊松比、密度和剪切模量进行按体积分数比例综合贡献得到,设Em为基体的弹性模量,Ef为硬涂层的弹性模量,Vm为基体的体积分数,Vf为硬涂层的体积分数,μm为基体的泊松比,μf为涂层的泊松比,则硬涂层薄壁圆柱壳等效材料的弹性模量E、泊松比μ、密度ρ和剪切模量G分别为

(1a)
μ=μfVf+μmVm
(1b)
ρ=ρfVf+ρmVm
(1c)

(1d)
硬涂层薄壁圆柱壳构件等效后的中面半径和厚度分别为
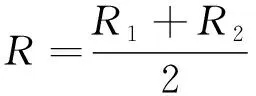
(2a)
H=H1+H2
(2b)
根据Love薄壳理论[21],任一区段硬涂层薄壁圆柱壳构件的振动微分方程表示为
(3a)
(3b)
(3c)

Kirchhoff面内切力Vx和横向剪力Sx分别为
(4a)
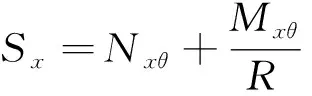
(4b)
中面法线绕x轴的转角θx、内力Nx和内力矩Mx的表达式分别为
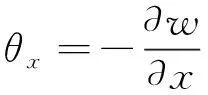
(5a)

(5b)
(5c)
令m表示硬涂层薄壁圆柱壳构件的轴向半波数,n表示周向波数,ωmn表示行波频率,定义位移解的形式为
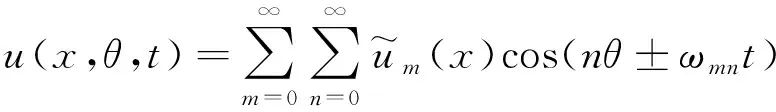
(6a)
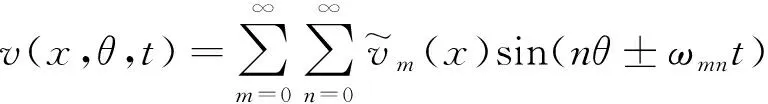
(6b)

(6c)
式中,“+”和“-”分别表示由于柯氏力和离心力引起的离心刚化效应,固有频率随转速变化产生后行波和前行波。
沿硬涂层薄壁圆柱壳构件的纵向分为n0个子段,n0=2j(j为自然数),共n0+1个截面,任一截面上的状态向量为
(7)
在状态向量中的位移、转角、内力和内力矩可以表示为
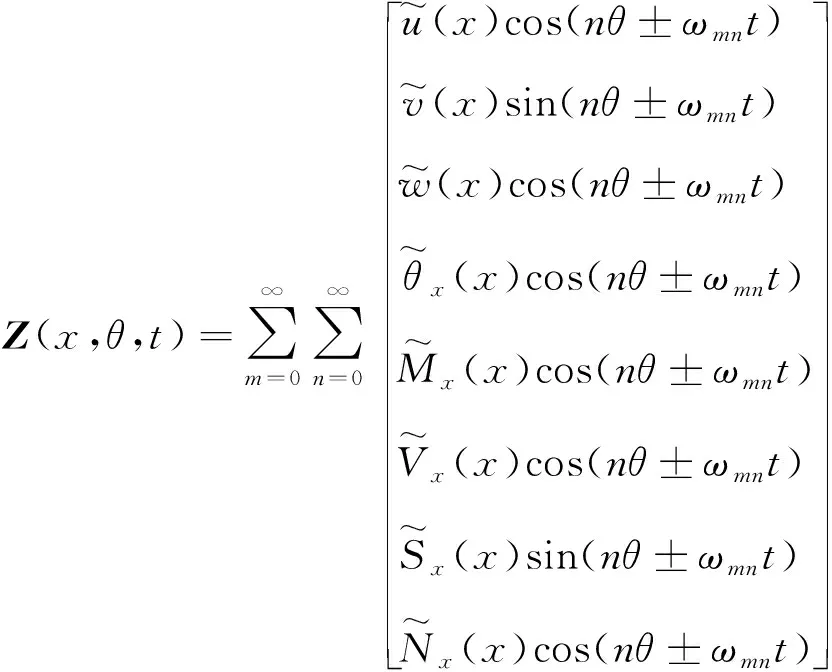
(8)
对上述变量进行整合,推导得到的一阶常微分方程组为
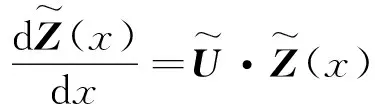
(9)

对于任一区段的相邻两截面,从一端面到另一端面的传递矩阵关系表示为

(10)
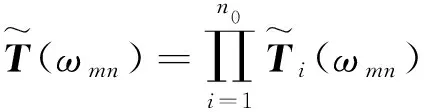
相邻两个截面的传递矩阵关系为
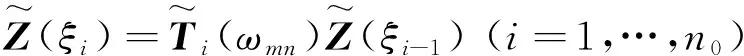
(11)
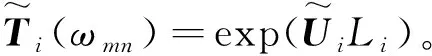
在简支-简支、固支-固支和固支-自由三种典型边界条件下,通过如下方法求解行波频率值:
(1) 简支-简支边界条件
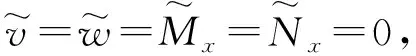
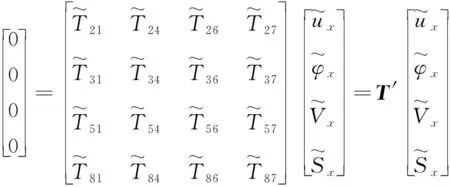
(12)
(2) 固支-固支边界条件
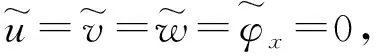

(13)
(3) 固定-自由边界条件
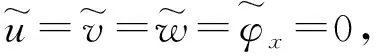

(14)
令式(12)、式(13)和式(14)的系数行列式分别为零,可以编程计算得到不同边界条件下的行波频率,即
det(T′)=0
(15)

(16)
由于外部复杂激振力作用的随机性,在实际中主要考虑周期激振力的作用,当激振力频率与行波频率有式(17)的关系时构件容易发生共振现象,即
ωmn=N·ωeN=1,2,3…
(17)
式中,ωe为激振力频率。
共振是一种能量聚集的现象,使构件发生危险的几率增加,为了判断构件在高速旋转时是否会发生共振现象,通过绘制Campbell图进行判断,在周期性倍频激振力作用下,激振频率表达式为
(18)
式中:K表示谐波系数;Nw表示工作转速。本文取K=1、2、3即可满足要求,Nw=1.5×104r/min。
当构件在启动、停止和变速工况条件下,工作转速附近的共振临界转速比较危险,应避开工作转速的±10%,一般用共振裕度[22]来描述,可以表示为

(19)
式中,Nr表示共振点对应的共振临界转速。
2 算例分析
针对高速旋转的硬涂层阻尼薄壁圆柱壳构件,在固支-自由、简支-简支和固支-固支三种边界约束条件下,采用本文方法沿壳体纵向分成16子段,基体所示的光滑薄壁圆柱壳材料为Ti5Al2.5Sn[23-24],两种硬涂层阻尼材料分别取NiCrAlY和NiCrAlCoY+YSZ,表1和表2分别给出了硬涂层薄壁圆柱壳构件的尺寸参数和材料参数,其中包括文献[19]的相关参数。

表1 硬涂层薄壁圆柱壳的几何参数
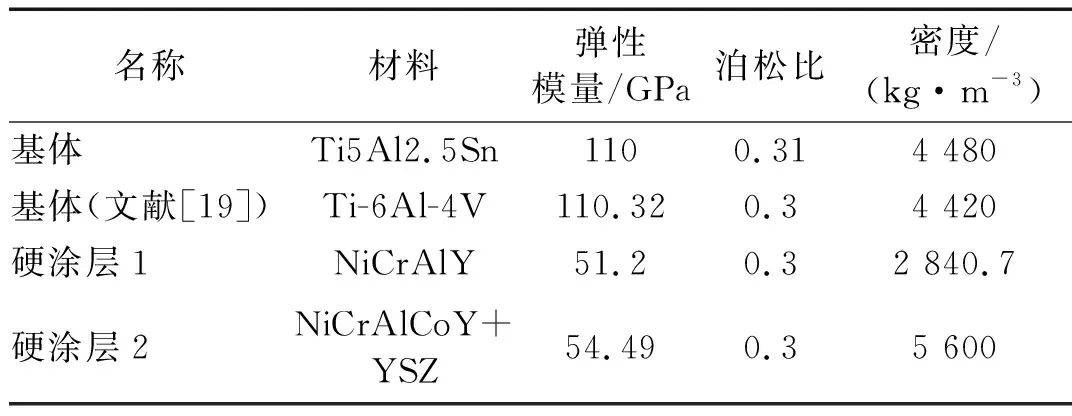
表2 硬涂层薄壁圆柱壳的材料参数
2.1 固支-自由边界条件
为了验证计算结果的准确性,利用本文方法,采用文献[19]中的参数进行计算,硬涂层材料为NiCrAlCoY+YSZ,得到的结果如表3所示。可以看出,本文方法和文献[19]得到的结果具有较好的一致性,各阶频率的平均误差约为1.15%,最大误差约为1.74%,误差在合理范围内,说明了本文分析方法的有效性。
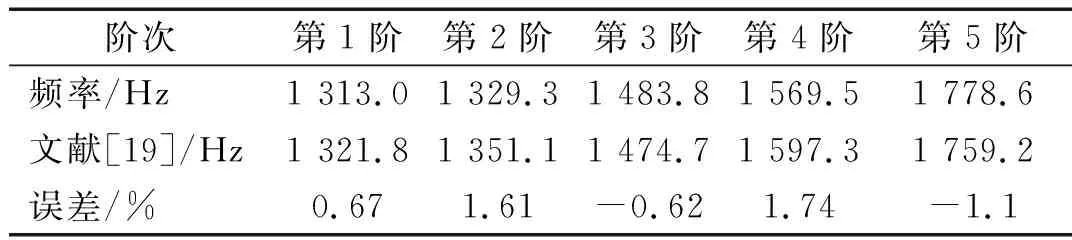
表3 硬涂层薄壁圆柱壳的前5阶固有频率
当转速在0时,对于NiCrAlY和NiCrAlCoY+YSZ两种硬涂层材料与文献[20]中不带硬涂层时薄壁圆柱壳构件,由式(15)和式(16)进行求解,对众多阶次筛选后得到的低阶静频值和三维模态振型如表4和图2所示。由表4和图2可知,当转速为0时,带有硬涂层1和硬涂层2时薄壁圆柱壳的最低阶静频值均对应(1,4)模态,与不带硬涂层时构件的最低阶三维模态振型相同,但静频值均减小,带NiCrAlY硬涂层薄壁圆柱壳的静频值减小了0.98%,带NiCrAlCoY+YSZ硬涂层薄壁圆柱壳的静频值减小了2.15%,同时其余各阶的静频值也发生了偏移。随着阶次的增加,带有硬涂层1和硬涂层2时硬涂层薄壁圆柱壳对应的三维模态振型相同,前六阶依次为(1,4)、(1,3)、(1,5)、(1,6)、(1,2)和(1,7),与不带硬涂层薄壁圆柱壳的模态振型完全相同,前六阶振型仍然以周向模态的振动为主,并且在自由端的振动幅度最大。

表4 固支-自由边界条件下薄壁圆柱壳的静频值

第1阶
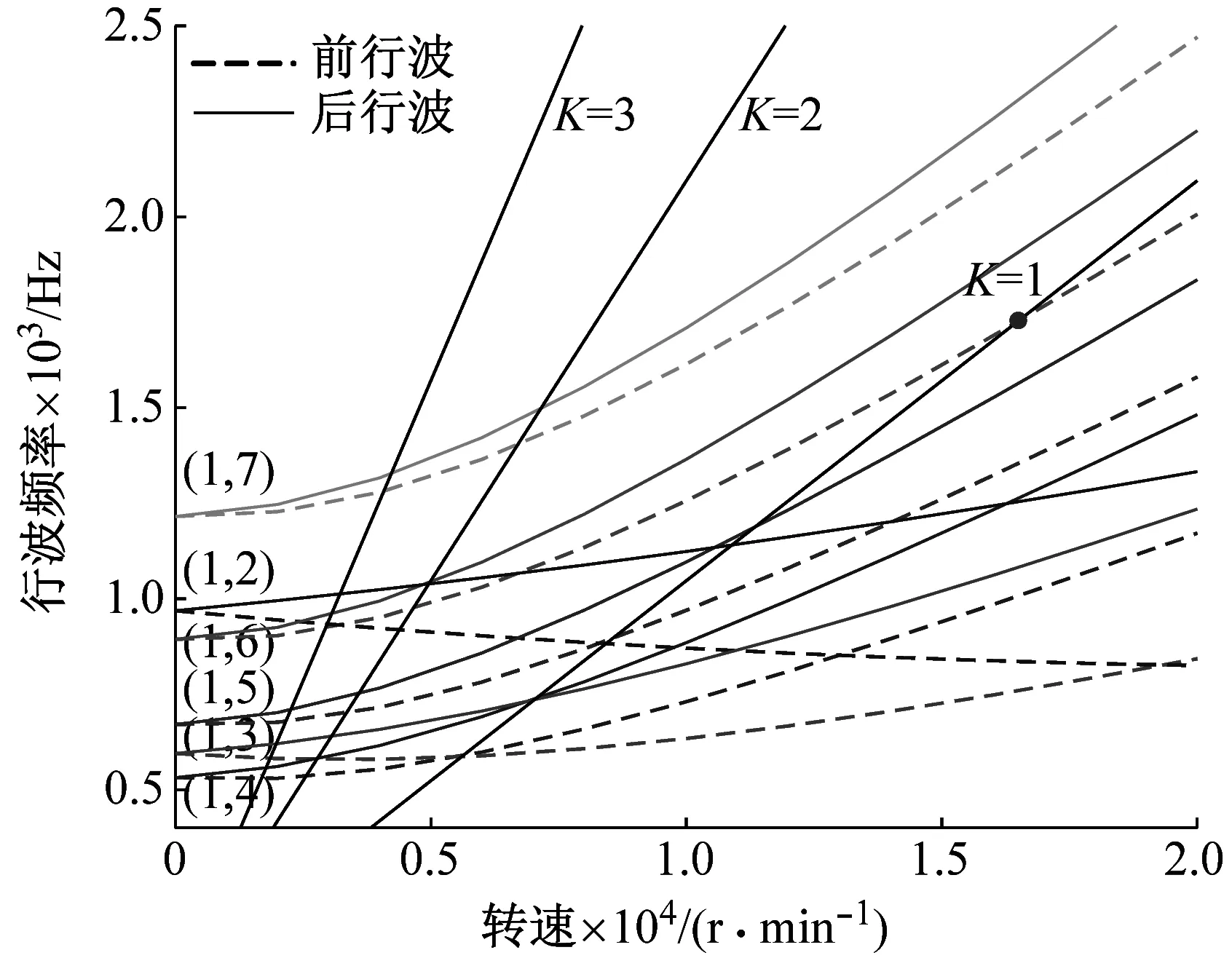
当转速为0~2×104r/min时,在转动坐标系下带有硬涂层1和硬涂层2时高转速薄壁圆柱壳的Campbell图如图3所示。可以看出,壳体结构的前后行波频率曲线随着转速的增加明显分离,在K=1、K=2和K=3倍频激励作用下,与前六阶模态的前行波和后行波的行波频率线存在多个共振点,但是K=2和K=3时激振频率线和行波频率线的交点都远离工作转速。在工作转速附近,硬涂层阻尼薄壁圆柱壳构件容易引起共振的共振点仅有1个,与不带硬涂层时构件的共振点数量相同。对于带NiCrAlY的硬涂层薄壁圆柱壳,在K=1倍激振力作用下,与(1,6)阶模态形成共振,而第1阶模态没有发生共振,共振频率为1 726 Hz,共振临界转速为16 484 r/min,与工作转速的共振裕度为9.89%;对于带NiCrAlCoY+YSZ的硬涂层薄壁圆柱壳,在K=1倍激振力作用时,同样和(1,6)阶形成共振,对应的共振频率为1 706 Hz,共振临界转速为16 290 r/min,与工作转速的共振裕度为8.6%。所以,不带硬涂层和带两种不同硬涂层时薄壁圆柱壳都容易引起(1,6)阶模态的共振,但是对应的共振频率和临界转速均增加。
(a) 硬涂层1
2.2 简支-简支边界条件
当转速在0时,对于NiCrAlY和NiCrAlCoY+YSZ两种硬涂层材料与文献[20]中不带硬涂层时薄壁圆柱壳构件,由式(15)和式(16)进行求解,对众多阶次筛选后得到的低阶静频值和三维模态振型如表5和图4所示。由表5和图4可知,当转速为0 r/min时,带有硬涂层1和硬涂层2时薄壁圆柱壳的最低阶静频值均对应(1,5)模态,与不带硬涂层时构件的最低阶三维模态振型相同,但静频值增加,带NiCrAlY硬涂层薄壁圆柱壳的静频值增加了3.15%,带NiCrAlCoY+YSZ硬涂层薄壁圆柱壳的静频值增加了1.93%,同时其余各阶的静频值也发生了偏移。随着阶次的增加,带有硬涂层1和硬涂层2时硬涂层薄壁圆柱壳对应的三维模态振型相同,前六阶依次为(1,5)、(1,4)、(1,6)、(1,7)、(1,3)和(1,8),与不带硬涂层薄壁圆柱壳的模态振型相比较,第2阶和第3阶振型发生了变换,但前六阶振型仍然以周向模态的振动为主,并且振动幅度最大部位发生在壳体中部。
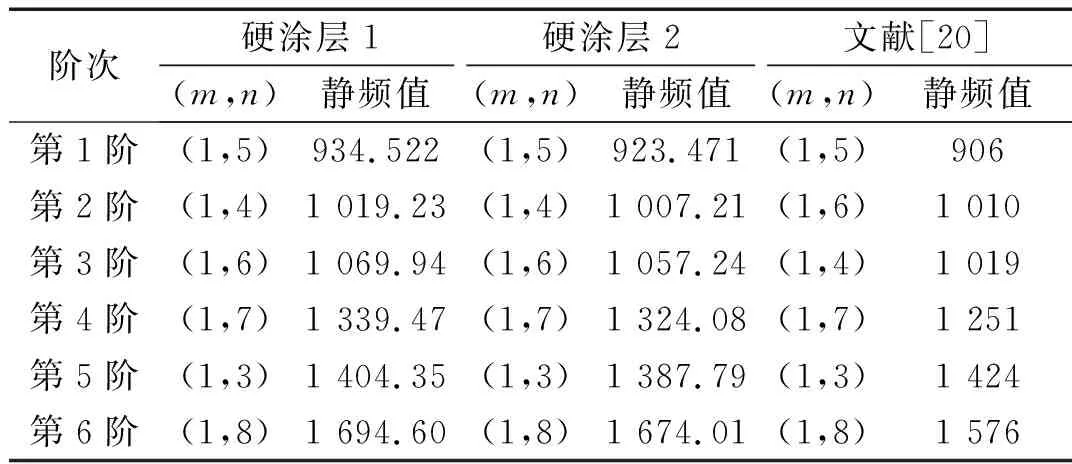
表5 薄壁圆柱壳的静频值

第1阶
当转速为0~2×104r/min时,在转动坐标系下带有硬涂层1和硬涂层2时高转速薄壁圆柱壳的Campbell图如图5所示。可以看出,由于柯氏力的作用,随着转速的增加壳体结构的前行波和后行波频率曲线明显分离。在K=1、K=2和K=3倍频激励作用下,与前六阶模态的前行波和后行波的行波频率线存在多个共振点,但是K=2和K=3时激振频率线与行波频率线的交点都远离工作转速。在工作转速附近硬涂层阻尼薄壁圆柱壳构件容易产生共振的共振点有2个,而不带硬涂层时构件的共振点仅有1个。对于带NiCrAlY的硬涂层薄壁圆柱壳,当K=1倍频激振力作用时,与(1,5)阶和(1,3)阶模态发生共振,共振频率为1 645 Hz和1 725 Hz,共振临界转速分别为15 709 r/min和16 474 r/min,与工作转速的共振裕度为4.73%和9.83%;对于带NiCrAlCoY+YSZ的硬涂层薄壁圆柱壳,当K=1倍激振力作用时,同样与(1,5)阶和(1,3)阶模态发生共振,共振频率为1 626 Hz和1 705 Hz,共振临界转速分别为15 529 r/min和16 279 r/min,与工作转速的共振裕度为3.53%和8.53%。所以,同不带硬涂层时的薄壁圆柱壳相比较,带两种不同硬涂层薄壁圆柱壳除了容易引起(1,5)阶模态的共振,还容易引起(1,3)阶模态的共振,对应的共振频率和临界转速均增加,并且共振裕度数值越小越容易引起对应阶次的共振。

(a) 硬涂层1
2.3 固支-固支边界条件
当转速在0时,对于NiCrAlY和NiCrAlCoY+YSZ两种硬涂层材料与文献[20]中不带硬涂层时薄壁圆柱壳构件,由式(15)和式(16)进行求解,得到的低阶静频值和三维模态振型如表6和图6所示。由表6和图6可知,当转速为0 r/min时,带有硬涂层1和硬涂层2时薄壁圆柱壳的最低阶静频值均对应(1,6)模态,与不带硬涂层时构件的最低阶三维模态振型相同,但静频值均变大,带NiCrAlY硬涂层薄壁圆柱壳的静频值减小了0.68%,带NiCrAlCoY+YSZ硬涂层薄壁圆柱壳的静频值减小了1.85%,同时其余各阶的静频值也发生了偏移。随着阶次的增加,带有硬涂层1和硬涂层2时硬涂层薄壁圆柱壳对应的三维模态振型相同,前六阶依次为(1,6)、(1,5)、(1,4)、(1,7)、(1,3)和(1,8),与不带硬涂层薄壁圆柱壳的模态振型相比较,第1阶和第2阶振型相同,其余各阶振型发生了变化,但前六阶振型仍然以周向模态的振动为主,在壳体中部的振动幅度最大。

表6 固支-固支边界条件下薄壁圆柱壳的静频值
第1阶
当转速为0~2×104r/min时,在转动坐标系下带有硬涂层1和硬涂层2时高转速薄壁圆柱壳的Campbell图如图7所示。可以看出,壳体结构的前后行波频率曲线随着转速的增加明显分离,在K=1、K=2和K=3倍频激励作用下,与前六阶模态的前行波和后行波的行波频率线存在多个共振点,但是K=2和K=3时激振频率线和行波频率线的交点都远离工作转速。在工作转速附近,硬涂层阻尼薄壁圆柱壳构件容易产生共振的共振点有3个,不带硬涂层时构件的共振点仅有1个。对于带NiCrAlY的硬涂层薄壁圆柱壳,在K=1倍激振力作用下,与(1,4)阶、(1,5)阶和(1,3)阶模态形成共振,而第1阶模态没有发生共振,共振频率分别为1 562 Hz、1 656 Hz和1 697 Hz,共振临界转速分别为14 917 r/min、15 814 r/min和16 208 r/min,与工作转速的共振裕度为0.55%、5.43%和8.05%;对于带NiCrAlCoY+YSZ的硬涂层薄壁圆柱壳,在K=1倍激振力作用下,同样与(1,4)阶、(1,5)阶和(1,3)阶模态形成共振,共振频率分别为1 544 Hz、1 637 Hz和1 677 Hz,共振临界转速分别为14 740 r/min、15 632 r/min和16 015 r/min,与工作转速的共振裕度为1.73%、4.21%和6.77%。所以,同不带硬涂层时的薄壁圆柱壳相比较,带两种不同硬涂层薄壁圆柱壳除了容易引起(1,3)阶模态的共振,还容易引起(1,4)阶和(1,5)阶模态的共振,对应的共振频率和临界转速均减小,并且共振裕度数值最小的(1,4)阶最容易发生共振,而在其它交点处的共振裕度均大于10%。
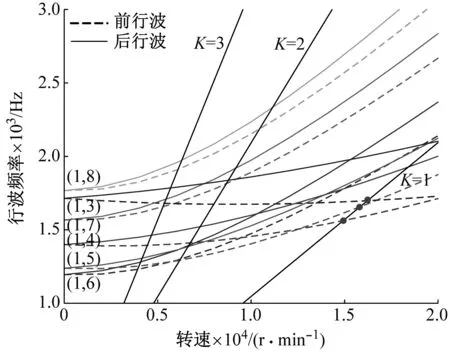
(a) 硬涂层1
3 结 论
本文基于Love薄壳理论、Viogt-Reuss原理和传递矩阵方法,在固支-自由、简支-简支和固支-固支三种边界约束条件下,通过算例分析了高速旋转硬涂层阻尼薄壁圆柱壳的行波共振特性,主要结论如下:
(1) 对固支-自由边界条件下硬涂层薄壁圆柱壳的固有频率进行计算,与文献中的结果基本一致,最大误差小于2%,验证了本文分析方法的合理性。
(2) 当转速为0时,在三种边界条件下NiCrAlY硬涂层比NiCrAlCoY+YSZ硬涂层薄壁圆柱壳的各阶静频值偏高,两种硬涂层材料对构件的第1阶模态振型无影响,仅静频值发生了偏移,随着阶次的增加和边界条件的变化,前六阶三维模态振型的顺序发生了变化。
(3) 在2×104r/min转速范围内,在三种边界条件下转速对两种硬涂层材料薄壁圆柱壳行波频率的影响较大,高转速时前、后行波频率曲线明显分离。在工作转速附近和倍频激励作用时激振频率线与前六阶模态的前、后行波频率曲线存在共振裕度小于10%的共振点,共振点数量与边界条件和倍频激振力有关。
(4) 对于高速旋转的两种硬涂层薄壁圆柱壳构件,随着边界条件的变化,共振模态不一定发生在第1阶,而是随着共振点变化容易引起对应阶次的模态振动,并且共振裕度越小越容易引起相应阶次模态的共振,通过调整构件的工作转速、固有频率或激振频率等措施,保证构件在工作转速时有充分的裕度,避免发生共振现象。
