固体火箭发动机声能共振规律试验研究

赵天泉， 张翔宇， 甘晓松

(中国航天科技集团有限公司四院四十一所，西安 710025)

固体火箭发动机不稳定燃烧又称为燃烧不稳定性或振荡燃烧，是发动机研制过程中遇到的棘手问题之一[1]。通常会产生压力-时间曲线和推力-时间曲线发生不规则变化、发动机或飞行器震动等现象。更严重时，会导致发动机因为超压而失效或爆炸[2]，导致延长研制周期和大量追加研制经费，甚至研制失败[3]。在过去几十年里，几乎在所有固体火箭发动机研究领域都出现了不稳定燃烧现象，如弹道、地对地、空对空、地对潜、舰对空导弹以及航天飞机和大型运载器等[4-5]。根据不稳定燃烧压力振荡频率与燃烧室声腔固有频率的关系，可以将不稳定燃烧分为声不稳定燃烧和非声不稳定燃烧[6]，其中声不稳定燃烧是燃烧过程与发动机中的声学过程相互作用的结果，是困扰发动机型号研制且难以彻底解决的问题。

发动机声腔结构对于涡脱落、结构阻尼、喷管阻尼等增益/阻尼因素以及燃烧室的固有振型、固有振荡频率具有较大的影响，多年来，研究人员对此开展了大量的研究工作。苏万兴等[7-10]通过试验及仿真的方式探究了潜入喷管对发动机内压力振荡的影响，研究结果表明，潜入喷管引入的空腔不利于发动机的稳定性；Dunlap等[11-12]对于绝热环引起的障碍脱落涡开展了研究工作；张翔宇等[13-14]对于后向台阶结构产生转角涡脱落引起声涡耦合现象进行了分析研究；苏万兴等[15]探究了空腔位置及结构对脉冲压力振荡的影响，发现头部空腔有利于提高发动机的稳定性，中间位置空腔及末端空腔发动机的稳定性较差，且扩张式中间空腔比收敛式中间空腔的压力振荡更为严重；闫宝祥等[16]建立了燃烧室声学特性分析的物理数学模型，并计算了四片翼柱型和五片翼柱型两种常见燃烧室形状的声学特性，为分析声不稳定燃烧提供了依据；Blomshield[17]研究发现，主燃面位于燃烧室的末端不利于发动机的稳定；张峤等[18]通过数值计算发现，头部空腔对压力振荡有一定的抑制作用。以上的工作主要考虑了结构变化对于流动的影响，且以仿真计算为主，声学过程是声不稳定燃烧的核心内容，本研究从声学角度出发，建立试验系统，探究声能共振规律。

建立了一种探究固体火箭发动机声能共振规律的试验方法并搭建了试验系统，以声学激励作为增益，考虑了发动机中的结构阻尼、壁面阻尼及喷管阻尼，从声学响应角度评估发动机稳定性。探究了前封头结构及潜入空腔体积大小对稳定性的影响规律，并从声学角度分析了原因。

1 试验原理

固体火箭发动机声不稳定燃烧是推进剂的燃烧过程(或燃烧室内的流动过程)与发动机燃烧室声振模式相互作用的结果，某一声模态是否稳定以及不稳定的幅值，取决于增益机制提供能量与阻尼机制耗散能量之间的关系。声学特性是声不稳定燃烧的核心内容，经典声学理论为理解和解释声不稳定燃烧提供了基本依据。

研究声不稳定燃烧时，可以将发动机视为自激声振荡系统，燃烧室相当于声振荡器，发动机中各种增益因素提供能源，同时还要考虑各种阻尼因素，典型的增益/阻尼因素如图1所示。

图1 固体火箭发动机常见的增益/阻尼因素

在试验中，声学试验发动机相当于振荡器，添加的声源作为增益，试验发动机出口处的声能损失、壁面损失及结构损失作为主要的阻尼因素，与实际发动机的工作情况相对应，试验原理图如图2所示。

图2 试验原理图

2 试验系统

2.1 试验系统组成

试验系统由声学试验发动机、声学激励系统及数据采集系统组成，如图3所示。其中声学试验发动机将在2.2中进行详细介绍。声学激励系统由声源、功率放大器及扬声器组成，声源为白噪声，经功率放大器通过扬声器传入试验发动机。扬声器位于发动机的头部及中部共两个，以便在不同位置添加声学激励。数据采集系统由传感器、模态数据采集测试仪及带有测试软件的计算机组成，试验发动机共分布40个传感器，以测量不同空间位置的声学响应，其中沿轴向分布10个，周向分布4个。

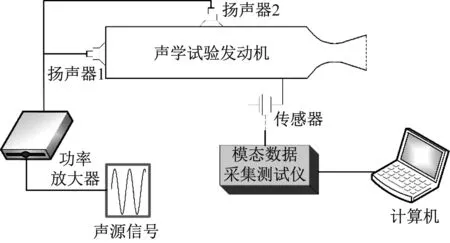
图3 试验系统组成示意图

2.2 声学试验发动机

声学试验发动机是试验系统的重要组成部分，由金属壳体及非金属填充物组成，二维结构示意图如图4所示，实物图如图5所示。其中金属壳体材料为铝，由前封头壳体、后封头壳体及中间试验段组成。非金属填充物材料为尼龙，由试验段填充物、前封头填充物及后封头填充物组成。改变前、后封头处非金属填充物结构可以改变试验发动机的声腔结构(表1)，对1#、2#,3#声腔结构开展试验可以探究前封头结构对声腔稳定性的影响，对4#、5#、6#声腔结构开展试验可以探究潜入空腔体积对声腔稳定性的影响。

1-前封头填充物；2-前封头壳体；3-中间试验段；4-试验段填充物；5-突扩连接件；6-后封头填充物；7-后封头壳体。

图5 声学试验发动机实物图

表1 声腔结构

3 试验方法

3.1 试验过程

声学试验发动机是一个声振荡器，添加的声源作为扰动并提供能量，二者耦合可产生声振荡，振荡的频率与声腔固有频率基本一致。由试验发动机中分布的传感器及测试设备可测得不同空间位置的声压值，改变前、后封头填充物构型可改变声腔结构，具体试验过程如图6所示。

图6 试验流程图

3.2 数据处理

定义声学响应传递函数pf表征压力振荡程度

(1)

式中：p为测点声压值;ps为声源声压值。

比较1#、2#、3#声腔结构的pf大小探究前封头结构对声腔稳定性的影响，比较4#、5#、6#声腔结构的pf大小探究潜入空腔体积对声腔稳定性的影响。(注：为了减小试验误差，试验中进行了重复测量，处理数据时对重复测量结果作均值处理。)

4 试验结果及分析

4.1 压力振荡特性

对于4#声腔结构，在头部添加声学激励时1号测点(测点编号与图3一致，下同)压力振荡特性如图7所示。试验发动机内部发生了压力振荡，各阶振荡频率呈现倍频关系(图8)，且前三阶振荡比较显著，第一阶振荡最为显著，在之后的分析中取前三阶压力振荡进行分析。

(a) 压力振荡曲线

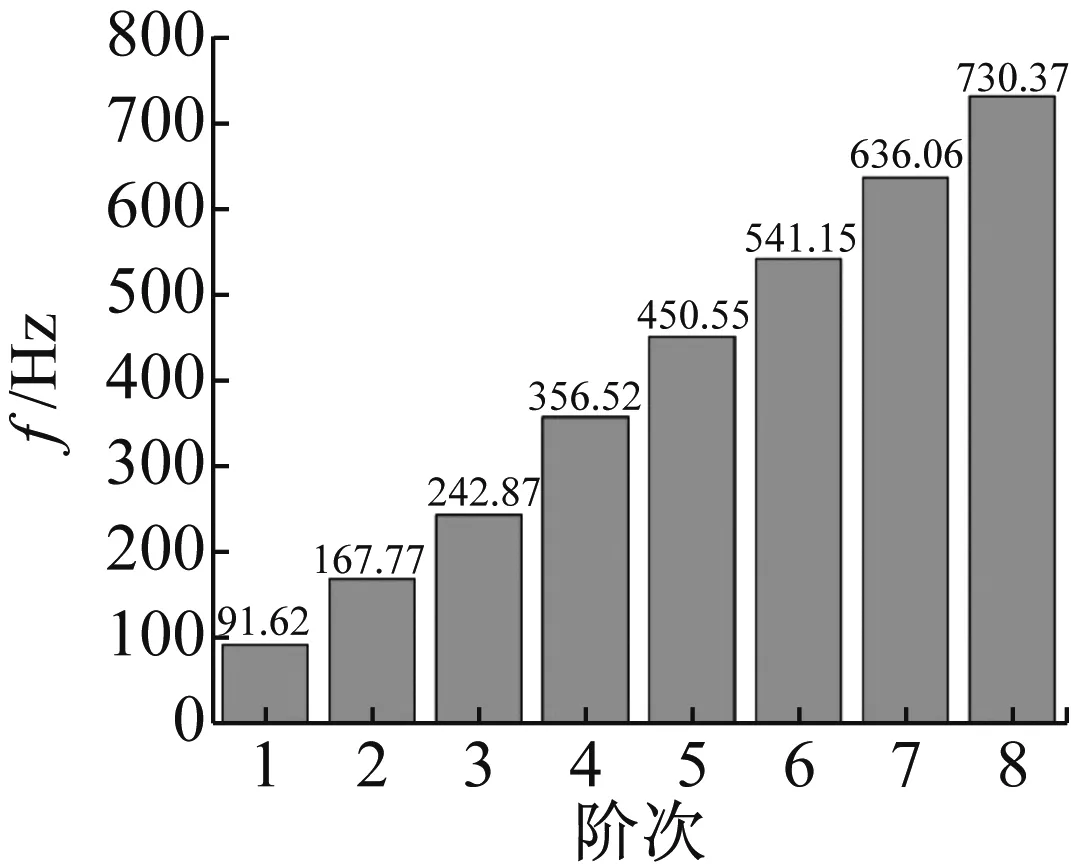
图8 振荡频率

分析前三阶压力振荡振型分布。对测点声压值进行插值计算，得到测点之间的压力分布，由试验发动机上的多个测点即可得到振型分布，如图9～图11所示。试验发动机内部发生了轴向压力振荡，与固体发动机轴向声不稳定燃烧对应。

图9 第一阶声压分布云图

图10 第二阶声压分布云图

图11 第三阶声压分布云图

4.2 结构特性对声腔稳定性的影响规律

4.2.1 前封头结构的影响

(1) 试验结果

对于1#、2#、3#声腔结构开展试验，由轴向振型分布可知，前封头处是压力振荡的波腹，振荡较为严重，选取1号测点进行分析，结果如图12所示。 三种声腔结构前三阶压力振荡频率基本一致。对于第一阶声学响应传递函数，3#声腔函数值最大，1#、2#声腔相差不大；对于第二、三阶声学响应传递函数，相比于2#声腔，1#、3#声腔函数值较大，稳定性较差。

(a) 1#声腔

(2) 结果分析

三种声腔结构声学响应传递函数在不同的阶次呈现的大小关系不同，对于第一阶传递函数，2#声腔结构对于声能的耗散作用更弱，函数值更大，稳定性更低；对于第二、三阶传递函数，相比于1#、3#声腔，2#声腔结构对声能的耗散作用更大，函数值更低，稳定性更高。

4.2.2 潜入空腔体积的影响

(1) 试验结果

对于4#、5#、6#声腔结构开展试验， 选取位于压力振荡波腹附近的1号测点进行分析，结果如图13所示。随着潜入空腔体积增加，各阶振荡频率减小，传递函数值升高，试验发动机稳定性降低。

(a) 4#声腔

(2) 结果分析

声波在发动机出口附近会发生反射与透射，改变潜入空腔体积会改变声压反射因数及透射因数。分析潜入空腔及出口处的传声特性，为便于分析，将结构进行简化(图14)。图14中:pi为入射声波;pr为反射声波;pt为透射声波;pb为潜入空腔处声波;S2为出口截面积，Sb为潜入空腔截面积，S1=S2+Sb;l为潜入空腔长度。沿试验发动机轴向建立坐标系，坐标原点位于潜入空腔入口处。

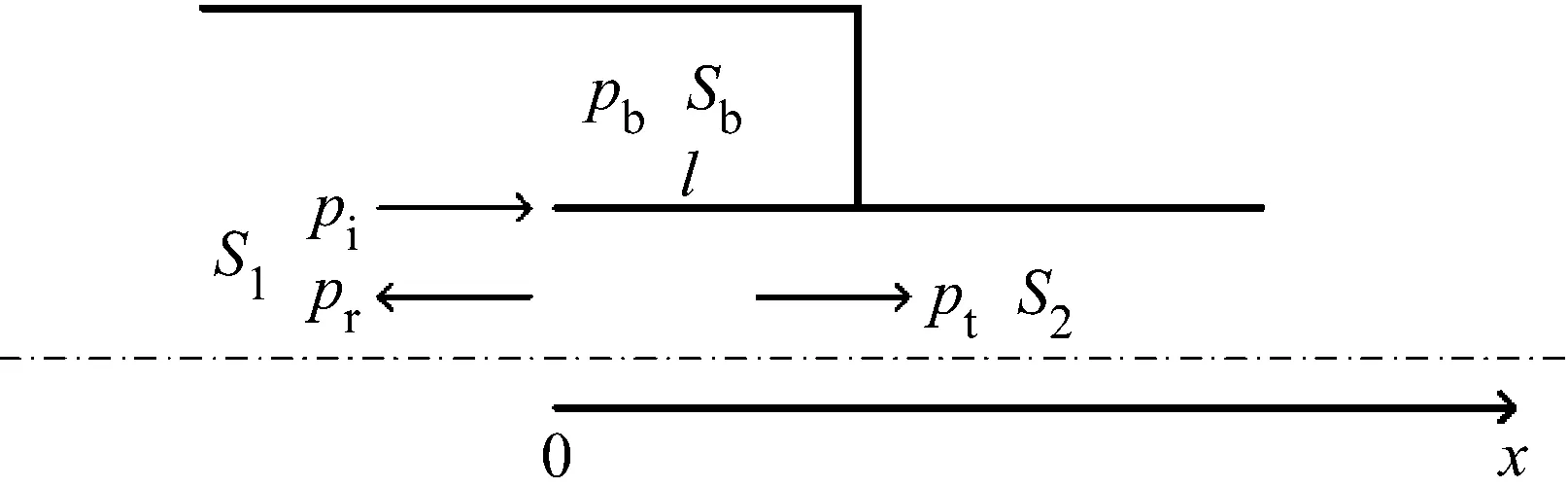
图14 传声特性分析示意图

管中各类声压的表达式为

(2)

在x=0的交接口，有声压连续与体积速度连续条件

(3)

或表示为

(4)

由式(10)、(11)及(12)可得

(5)

则声压透射系数

(6)

式中，Zb=Rb+jXb

则声强透射系数为

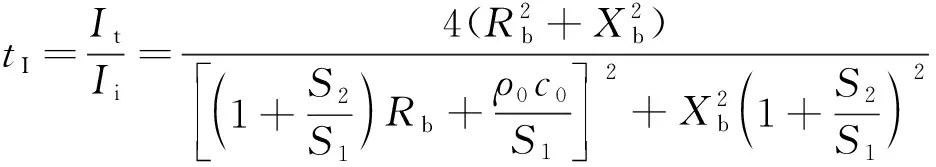
(7)

声功率透射系数为

(8)

代入式(8)中，得到：

(9)

试验中，S1=0.066 m2，Sb=0.038 m2，则S2=0.028 m2，取c0=340 m/s，4#、5#、6#声腔对应的l分别为0、0.05 m、0.10 m，作出三种潜入空腔长度下声功率透射系数随频率的变化曲线，如图15所示。在所分析的频率范围内，随着潜入空腔长度的增加，各阶振荡频率处声功率透射系数减小，导致试验发动机内部声学响应传递函数升高。

图15 不同潜入空腔长度下声功率透射系数

5 结 论

(1) 从固体火箭发动机声不稳定燃烧的声学特性出发，以声学激励作为扰动并提供能量，通过声学响应传递函数表征发动机稳定性，建立了试验系统并开展了试验，可以表征声不稳定燃烧的声学特性。

(2) 不同前封头结构声腔的各阶振荡频率基本相同，对于第一阶压力振荡，3#声腔函数值最大，1#、2#声腔差别较小；对于第二、三阶压力振荡，相比于1#、3#声腔，2#声腔结构对声能的耗散作用更大，稳定性更高。

(3) 潜入空腔体积增大，各阶压力振荡频率减小，声学响应传递函数升高，声腔稳定性降低。传声特性分析结果表明，潜入空腔长度增加导致出口声功率透射系数减小，声腔内声学响应传递函数升高，声腔稳定性降低。