随机扰动下多电机网络混沌振荡的反馈可调节控制

郭士铭， 韦笃取

(广西师范大学 电子工程学院，桂林 541004)

永磁同步电机(permanent magnet synchronous motor，PMSM)具有高功率密度、高转矩密度、高效率、高稳定性等特性[1-2]，被广泛应用于工业生产与日常生活中[3-4]。然而永磁同步电机是多变量、强耦合的非线性系统，在某些参数条件下会出现混沌行为，混沌会造成电机间歇振荡，进而影响电机的工作状态[5]。另一方面，在现代工业生产中，需要多电机网络的稳定协调同步运行[6]，多电机网络一旦出现混沌振荡，将会影响电力传动系统的工作效率，造成极大的经济损失。此外，实际生产过程中，电机系统由于受到随机噪声及随机负荷的影响而具有随机性[7]，使多电机网络的控制工作变得更复杂。因此，研究随机扰动下多电机网络的混沌控制对保证工业生产的高效安全运行具有重要意义。目前，国内外学者提出了较多的复杂网络混沌控制理论与方法，如有限时间控制[8]、间歇性控制[9]、滑模控制[10]，等等。但有关电机网络的混沌控制研究尚属少见。本文将在前人的工作基础上提出反馈可调节控制方法对随机多电机网络混沌进行控制。

反馈可调节是指将非线性控制系统的反馈进行调节，使系统达到稳定状态。已有文献研究表明，对单个非线性系统的增益进行自适应调节后，可以有效控制混沌[11]。本文首先以PMSM为节点，以电机间的耦合为连边，建立随机扰动下不同拓扑结构(Newman-Watts,NW)小世界网络，星型网络)的多电机网络模型，然后基于李雅普诺夫稳定性理论提出反馈可调节控制方法，对多电机网络的混沌进行控制。最后数值仿真验证了控制方法的可行性和有效性。研究结果对保证电力传动系统正常运行具有指导意义。

1 PMSM动力学模型

目前广泛研究的永磁同步电机模型为三维自治系统[12-14]，其数学模型如下

(1)

式中:x1、x2、x3分别表示系统的状态变量;σ、γ是系统无量纲参数，均为正值。已有文献研究表明[15]，PMSM系统在一定的系统参数范围内会出现紊乱无周期的混沌状态。以系统(1)为节点，电机间的耦合为连边，建立多电机网络，其数学模型如下

(2)

式中:i为节点编号;c>0为耦合强度。Aij表示网络的拓扑连接：如果网络节点i和j之间存在连接，则aij=aji=1；否则，aij=aji=0。同时,对所有i，有aii=0。

2 随机扰动下PMSM网络模型

对于一般随机非线性系统可以描述为如下模型

dx=f(x)dt+h(x)dw

(3)

其中x∈Rn是系统的状态变量，w表示定义在完备概率空间上的r维布朗运动，f(·):Rn→Rn和h(·):Rn→Rn是在x上的局部Lipschitz函数，且满足f(0)=0和h(0)=0。

定义1：对于给出的V(x)∈C2，结合差分公式(3)，定义差分运算L如下

(4)

式中,Tr{A}是A的迹。

引理1[16]：对于随机系统(3)，如果随机非线性系统的李雅普诺夫函数为负定，则系统在区间上存在唯一解，且系统趋于稳定。

将PMSM系统与式(3)相结合，可得到随机多电机网络模型[17]

(5)

式中,Ψ1i，Ψ2i，Ψ3i表示任一节点未知的平滑非线性函数。

3 多电机网络的反馈可调节控制设计

设计如下控制器

(6)

式中,β，k，m均为控制器参数。将控制器加入系统(5)得

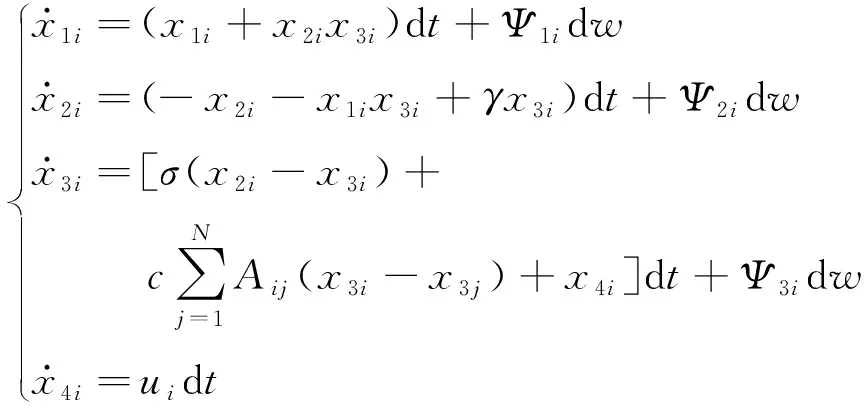
(7)

式中，x4i为系统的反馈。下面我们通过李雅普诺夫稳定理论来验证控制器的可行性。

将Vi按照式(4)进行差分运算

(8)

只需满足差分算式LVi<0即可说明受控系统为渐近稳定的。

根据文献[11]对差分式的分析，当Vi为正定函数且系统为随机非线性系统时，差分式(8)各项均满足以下关系式

(9)

(10)

式中:C1，C2，C3为正常数;k≥0为控制器参数;ε，b是待定系数。

结合关系式(8)～(10)可得

LVi≤k-1-2ε-b(C1+1)||x1i||4+

(11)

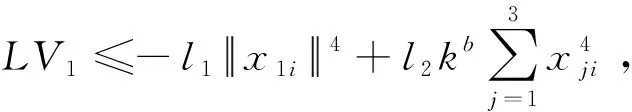
||x1i||4[k-1-2ε-b(C1+1)-l1+k-1-2ε-b]+

-|x1i||4[-k-1-2ε-b(C1+2)+l1]-

(12)

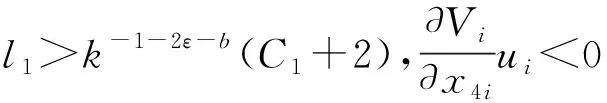
k-1+l2kb>k-1-ε(C2+2C3+1+C4)

则可得LV为负定，系统趋于稳定。

4 实验仿真

控制器u具体表达式如下

u=-(β1β2β3k-m1x1+β2β3k-m2x2+β3k-m3x3)

(13)

根据以上推论与条件，设置控制器参数为：m1=3，m2=2，m3=1，k=3，β1=2，β2=2.11，将参数代入式(13)可得

u=-(0.3k-m1x1+0.5k-m2x2+0.7k-m3x3)

(14)

首先分析反馈可调节控制器对NW型小世界电机网络的影响。网络的拓扑实现过程如下：从一个节点数N=50，近邻数m=2的最近邻耦合电机网络开始，然后在非近邻节点之间以概率ρ随机添加连边。对于ρ=0，它就退化成原来的最近邻耦合网络；对于ρ=1，它就变成一个全局耦合网络。系统参数取γ=28，ρ=0.7，c=3。系统在无反馈调节控制时，各节点时序如图1所示。

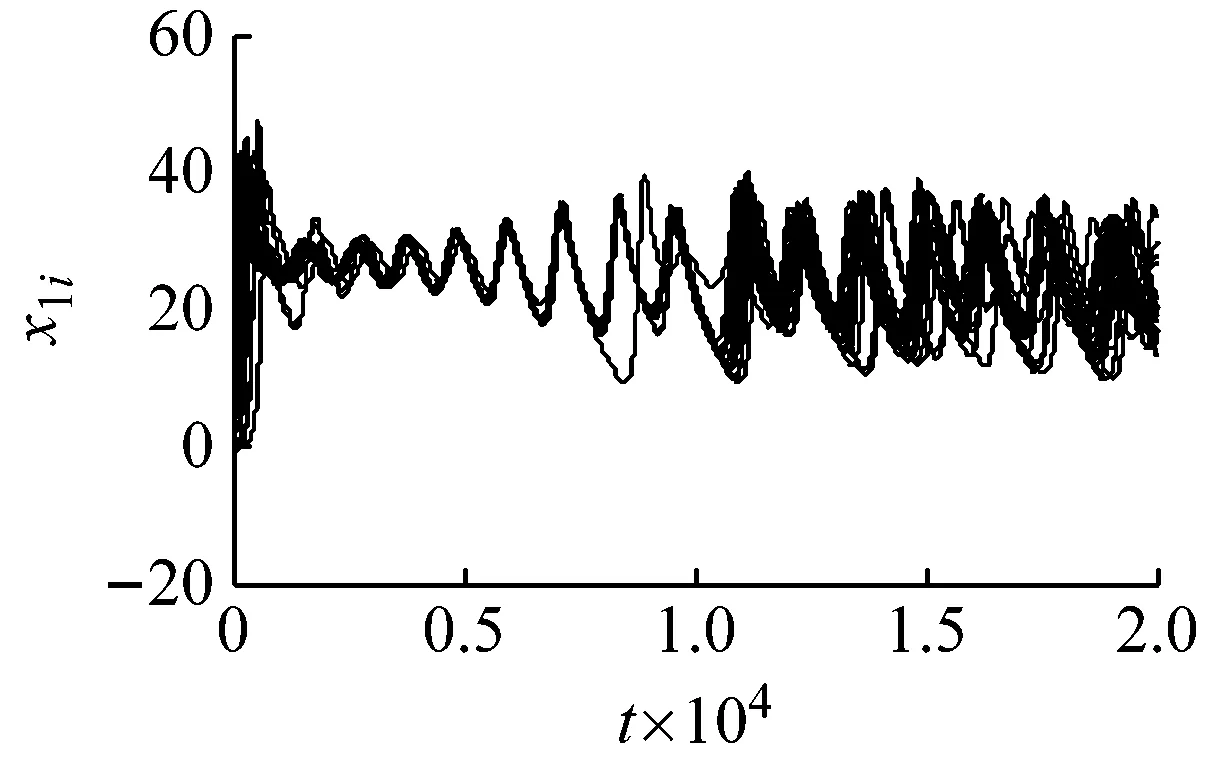
(a) x1i时序

从图1可知，在NW小世界电机网络中当随机非线性系统中未加入反馈调节控制时,多电机网络处于混沌状态，各电机节点均处于无规则振荡状态中，通过对比图1(a)，(b)和(c)可知，系统变量x3i振荡幅度最大，故在实验仿真中控制器加到系统变量x3i中。

从图2可知，在NW小世界中加入反馈调节控制器后，各节点的系统状态变量曲线均在短时间内趋于稳定，说明在NW小世界电机网络中加入反馈调节控制器能有效抑制系统混沌。

(a) x1i时序

接着分析反馈调节对星型电机网络的作用，节点数取50，系统参数取γ=28，σ=5.6，c=3系统在无反馈调节控制时，状态变量如图3所示。

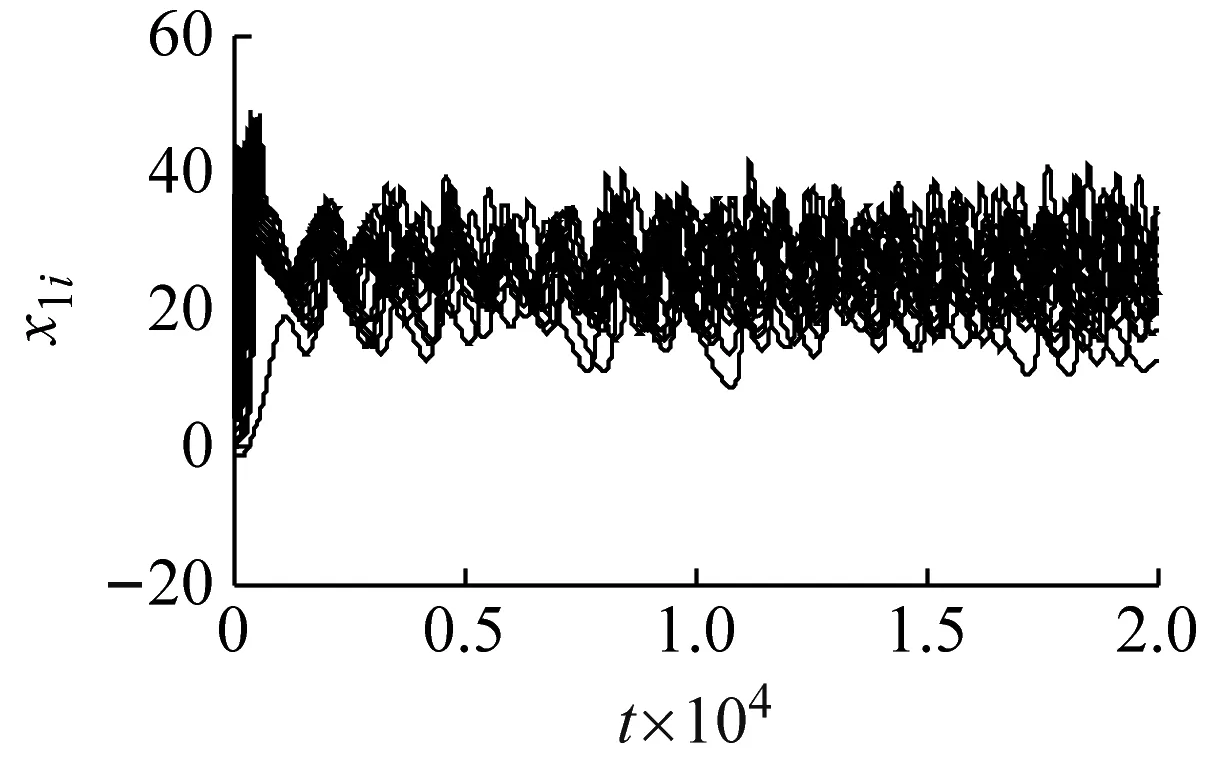
(a) x1i时序

从图3可以看出，星型电机网络在没有反馈调节控制时处于混沌运动状态。然后在系统中加入反馈调节控制器，系统的状态变量如图4所示。

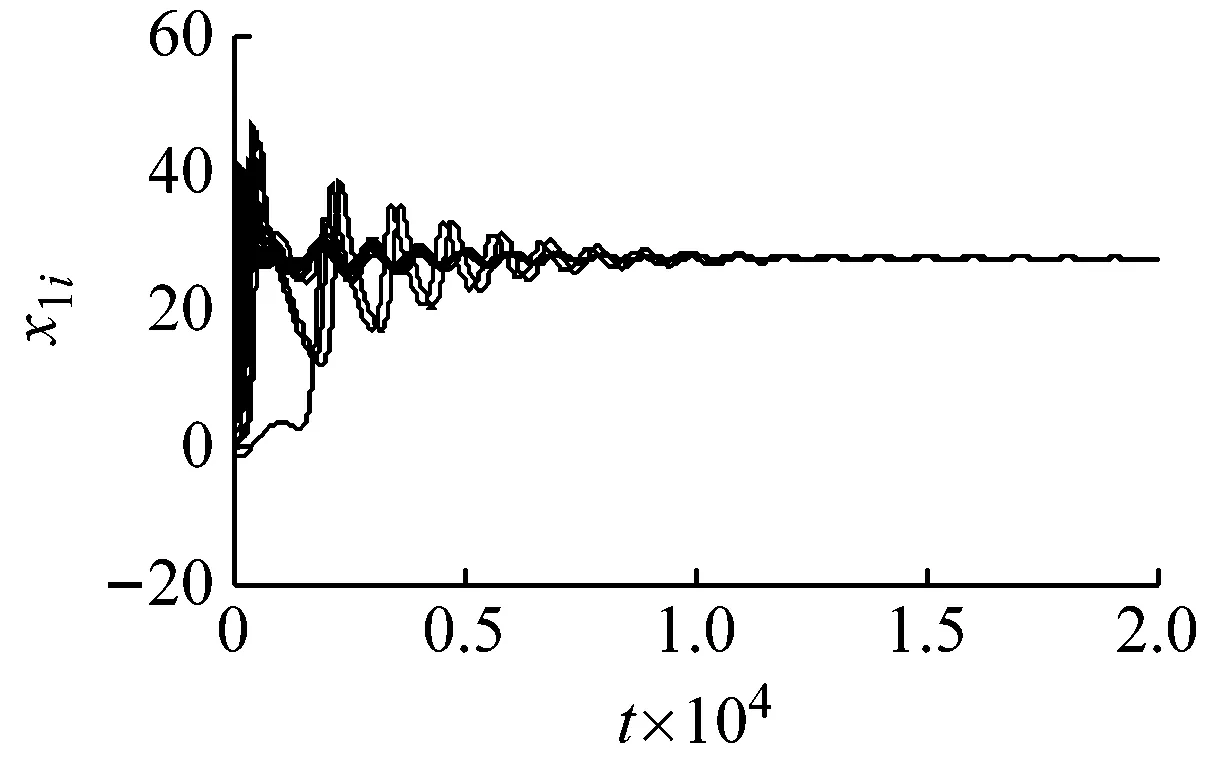
(a) x1i时序

从图4可知，系统在加入反馈调节控制后，星型电机网络各节点的混沌振荡得到了有效控制，但状态变量时序图趋于稳定所需的时间较长。仿真实验结果表明反馈调节控制同样适用于星型电机网络，但对于NW小世界电机网络中的混沌控制效果更优。

5 结 论

本文利用反馈可调节控制方法对随机扰动下多电机网络的混沌进行控制。首先以PMSM为节点，电机间的耦合为连边，建立具有不同拓扑结构(NW小世界网络，星型网络)的多电机网络随机模型，然后提出了一种反馈可调节控制方法，并基于李雅普诺夫稳定性理论证明了该方法的可行性。最后运用数值仿真方法对理论分析的有效性进行了验证。本文研究结果对保证多电机复杂系统的正常工作有一定的指导意义。