考虑时空影响下的图卷积网络短时交通流预测

陈丹蕾，陈 红，任安虎

西安工业大学 电子信息工程学院，西安710021

近年来交通拥堵现象严重，且拥堵时的尾气排放不仅造成环境污染也导致大量能源浪费；道路拥挤造成交通事故的频发，都给交通治理带来考验。道路车流量预测是近年来交通领域的研究热点之一，在路网不同道路上的检测器中采集到车流量数据，通过一些方式学习到其中的数据规律，去预测未来时刻不同路段的数据。文献[1]在路易斯64号州际公路的数据上研究了四类传统机器学习交通流量预测的方法：分布式随机森林、深度神经网络、广义线性模型和梯度提升机。其中分布式随机森林方法所得模型略微胜于其他三种方法所得模型。为防止交通流的不确定性带来噪声干扰，同时为提高预测的准确性，文献[2]建议采用小波分解法获得原始交通数据的基序列和偏差序列。并对比了局部加权偏最小二乘法（LW-PLS）和卡尔曼滤波法，结果表明文中方法的准确率确实有所提高。考虑到神经网络组合模型性能优于单模型，将k-近邻（KNN）与长短时记忆（LSTM）结合[3]，利用KNN 选择检测站并将构造的交通序列集数据送入LSTM预测。文献[4]组合了ARMA模型和BP神经网络模型，以道路路口为单元做预测，但没考虑路口的交通流方向。STARIMA[5]预测模型利用包含多阶路口的路口转弯率来构建空间上的权重矩阵，虽考虑了交通流方向但没有考虑现实因素中人的主观因素对路线选择的影响，只考虑了最优情况。在大型的路网结构中为了预测交通拥堵，Ma等人[6]融合了深度受限玻尔兹曼机和递归神经网络，由于RNN模型自身限制无法处理长时间序列，Shao 等人[7]利用LSTM 模型进行预测，虽克服RNN存在的问题，但层数限制导致LSTM模型优势没被体现，预测效果不佳。为加深层数并提高预测精度，提出深度信念网络（DBN）和多任务学习（MTL）组成的深度框架[8]，二者间可通过权重共享使精度提高近5%。路网结构类似于拓扑结构，在图论中可以表现为图结构数据，可利用图卷积网络在图结构上做数据信号的处理。文献[9]提出时空图卷积网络（STGCN），相比传统CNN和RNN提高了计算效率，可以很好地学到时空特征中的有用信息。为了能够在实际路况中随着时间变化过程动态地捕捉到空间的依赖关系，用动态图卷积的思想对STGCN的空间静态依赖提出时空GCNN[10]来做改进；不同周期的流量数据也是捕获数据时空特性的关键，利用时空卷积对其分别建模提出多组件时空图卷积网络[11]（MCSTGCN），真实数据预测后效果优于部分现有模型；利用基于注意力的方式在模型中突出重要的数据部分，文献[12]提出图和基于注意力的长短期记忆网络（GLA）的混合以捕获交通流的时空特点。图卷积网络（GCN）提取观测站上的交通流的空间特征，长短期记忆（LSTM）模型提取到交通流的时间特点。为了在大规模数据上进行预测，Gao等人[13]提出一种大规模的可学习的图卷积网络（large-scale Learnable GCN，LGCN），取特征值大的前几个结点作为邻居结点最终得到邻居结点的信息。Zhao 等人[14]提出将图卷积网络与门控循环单元组合模型，在出租车和高速公路环路上数据集上预测车速，并加入随机噪声检验模型的鲁棒性，结果表明所提模型具有更好的性能，但是并没有考虑到城区路网内交通流之间的特性。

综上所述，充分考虑到城区路网的结构特性，以及交通流预测需要同时考虑时空因素的特点，采用图卷积网络与门控循环单元组合构成一个包含五层神经网络层的深度神经网络，先根据真实路网中各路段之间的相邻关系构造路段之间的邻接矩阵作为图卷积网络的有向图数据，将采集到的车流量数据与邻接矩阵一同作为图卷积网络的输入，用经过GraphSAGE 算法改进后的图卷积网络采集并聚合相邻路段所提取到的含有空间特征的车流量数据。再结合门控循环单元可以处理时间序列数据的特点，将图卷积网络中已经降维的输出数据作为其自身的输入，由此提取出含有时间特征的1维向量作为最终的预测结果，根据实验得出的结论验证了模型的有效性，证明本文模型可以很好地预测城区道路的车流量。

1 图神经网络（GNN）

1.1 图卷积网络（GCN）

图卷积网络[15]是为解决拓扑结构数据，提高网络效率且更好地提取数据空间特征而提出，图卷积网络计算原理如图1 所示。图卷积网络中的结点关系是用图来表示，对图进行定义：G=(V,E)，其中V(vertices)是图中结点的集合，E(edges)是结点之间边的集合，结点代表各路段的采集器，边代表路段，箭头代表方向。在交通网络中，交通数据是有向的且在真实路网中采集器采集到的数据都是单向的，因此这里定义的是单方向的有向图（如图2所示）。

图1 图卷积网络计算原理图

图2 交叉路口不同方向车流量行驶情况

图2 中黑色圆点代表每个道路口的采集器（传感器），每条路段都有1个采集器，分别记录进入车道车辆和通过车道车辆，代表从图中车道的初始位置开始可能通行的各个方向，红色方框的部分代表一个交通路口，箭头指向代表车辆通行（车道）方向。

图卷积层卷积操作和激活函数定义如下：

其中，Hl+1∈ℝM×Nl+1为l+1 的隐含值；Hl∈ℝM×Nl为l层的隐含值；X∈ℝM×N为输入；M为结点数量；N为每个结点上的特征数量；为了在结点中引入自身结点，再定义一个单位对角矩阵I，使得；f为l层到l+1 层的传播函数，将各结点特征聚合后利用它的传播规则生成下一层的特征值。其传播规则如下：

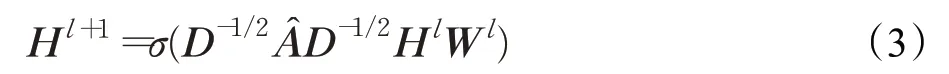
其中，σ为l层的非线性激活函数（relu激活函数）；度矩阵，i、j分别为结点vi与结点vj，D-1/2为对度矩阵D求逆后开根号，可以看作是用来给度结点的特征值进行归一化从而降低不同度数量上特征值之间的差距，防止后期训练过程中出现梯度消失或梯度爆炸的现象，Wl∈ℝNlNl+1为l层的权重矩阵。

1.2 GraphSAGE算法

GraphSAGE[16]的核心是通过训练聚合函数聚合邻居结点特征信息，将基线的图卷积网络学习扩展为归纳学习，使得利用该算法改进后的GCN 对未知结点起到泛化的作用。定义l个聚合器aggregatel,∀l∈{1,2,…,l}在聚合器上定义聚合函数来聚合邻居结点信息到目标结点上，聚合过程如下所示：

以图3中红色结点为中心向外采样，l=1 代表第一层采样的邻居结点，聚合邻居结点的特征信息，l=2 代表第二层采样到二阶结点，聚合到二阶邻居结点的特征信息。为了尽可能保留车流量较多的特征，本文中每一层的聚合算子采用加和聚合算子，如公式（6）所示：

图3 某路口结点两层采样和聚合的过程

1.3 图注意力机制（GAT）

在图算法中，图注意力机制[17]需要先计算目标结点与邻居结点之间的注意力系数，在路网中可以描述为两路段之间车流量流动越大系数越大。这些系数作为权重在聚合邻居结点信息时进行加权，在图神经网络计算中能更关注系数大的邻居结点，从而增加大车流量路段预测的准确性，路段间的车流量关系也很容易被发掘。设邻居结点v到vi的权重系数为eiv，激活函数设计为LeakyReLU，权重参数为a∈ℜ2d(l+1)，则权重系数计算公式为：

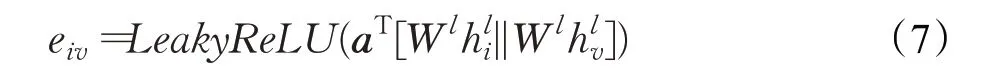
为能更好地分配权重，对所有的邻居计算出的相关度统一地做形式为softmax 归一化处理，保证所有邻居的权重系数和为1，得到最终的权重系数αiv：

最后根据注意力机制的加权求和思路，更新后的结点v特征值为：

2 门控循环单元（GRU）

门控循环单元是为解决循环神经网络（RNN）中无法保留长时间依赖信息以及反向传播过程中出现的梯度消失和梯度爆炸现象。但是相比LSTM 能够提高运算速度[18-19]，同时在性能上影响较小，在不同时间段的特征值中保留下来出现频率较高的特征。GRU神经网络单个细胞内部原理图如图4所示，在每个隐藏神经元单元中都有两个门控，分别为更新门zt决定是否将前边时间段的信息传递进来、重置门rt决定该遗忘多少信息、经过重置门之后剩下的部分被称作候选状态，在输入时间数据后该网络会根据所输入数据长度确定时间序列长度，并且在一个时间步里，所有神经单元会同时并行处理数据。

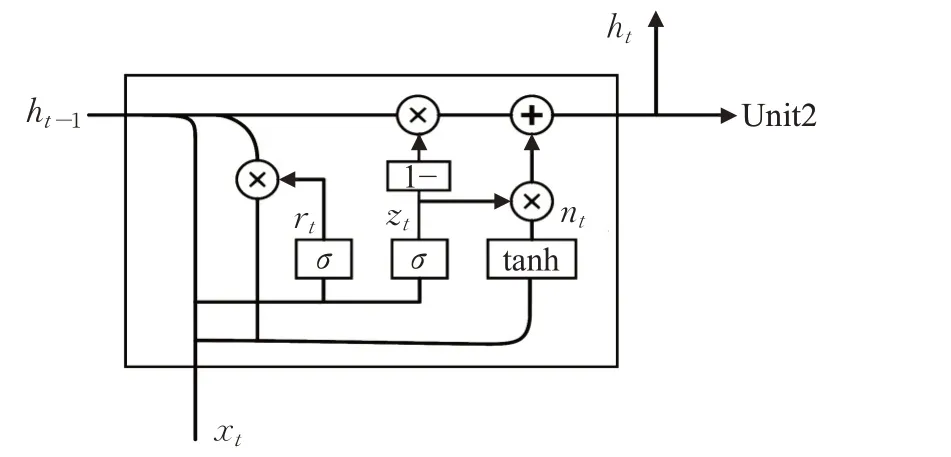
图4 GRU隐藏单元内部原理图

式（10）～（13）中为GRU隐藏单元内部计算原理：

其中，xt为输入，ht-1为上一时刻的隐藏状态，ht为新细胞状态；rt为重置门值，zt为更新门值，为候选状态；win、wir、wiz分别为两个门和隐藏状态的输入的权重，whn、whr、whz分别为两个门和隐藏状态的隐藏层权重，bin、bir、biz分别为两个门和隐藏状态的输入偏置，bhn、bhr、bhz分别为两个门和隐藏状态的隐藏层偏置；σ为sigmoid激活函数，“∗”为哈达玛积。

3 GCN与GRU组合预测模型

给定一个包含有M条路段，N天历史车流量数据，则需要定义该路网第n天的车流量数据矩阵Sn为：

如图5所示为路网拓扑结构，每一条线代表一条路段，两路段的交点即为一个路口，每条路段均安置一个检测器，对应编号既为路段编号也为检测器编号。以编号为A 的路段为例，“①”代表车流从A 路段分别到一阶邻居结点路段B、D、F的车流量，“②”以及灰色指向箭头代表车流经过一阶邻居结点路段到二阶邻居结点路段B1、B2、B3、D1、D2、D3、F1、F2、F3 的车流量，起始路段与其邻居路段间指向关系如表1所示。

图5 路网拓扑结构图

表1 A路段对应一二阶邻居路段

预测模型建立过程如下：

（1）GCN 参数配置。为了降低计算复杂度节约计算资源，在图卷积网络中设定聚合器l=2，采样结点数为10，并在每一层的前向传播过程中加入图注意力机制方法。

（2）GCN 第一层结点设置。图卷积网络的第一层输入为144×N（N天每天144个时间点）个结点，输出为350个结点。

（3）GCN 第二层结点设置。图卷积网络的第二层输入为350个结点，输出为220个结点；其中图卷积层每一层接收到所有特征数据后，会利用空间相关性根据不同的权重进行降维。

（4）GRU 第一层神经单元设置。门控循环单元的第一层隐藏神经单元个数为100，输入维度为图卷积网络的输出维度。

（5）GRU 第二层神经单元设置。门控循环单元的第二层隐藏神经单元个数为10。

（6）全连接层设置。最后一层为全连接层，神经元个数为1，其输出值为最终的预测结果。

预测模型结构如图6所示。

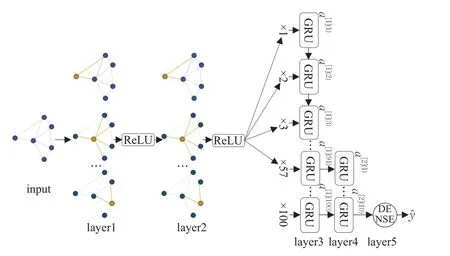
图6 模型结构

4 实验结果分析

4.1 数据介绍

为了增加评估模型的有效性，本实验数据采集于陕西省榆林市区某中心区域如图7 所示，该数据集中共涉及到16 个路口，57 条路段，数据点以周期10 min为一个间隔，从8：30—21：30 共10 天正常工作日，共包含45 030 个车流量数据。其中训练数据为前6 天，测试数据为后2 天，为观察模型的训练效果，取第7 天和第8 天的数据作为验证集。图7 中绿色线表示所涉及路段，线段上方框中1～16 数字代表路口编号。为便于观察路网中每条路段的具体位置，画出图7 区域的路段拓扑结构图如图8 所示，每条路段都对应着该路段的路段编号。

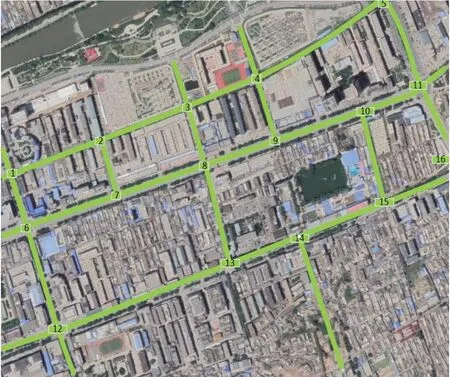
图7 本实验采集数据的真实路网区域

图8 本实验路网区域拓扑结构图

模型算法设计如下：

（1）根据一阶邻居结点指向关系构造邻接矩阵adjacency=R57×57。

（2）定义一个单位对角矩阵I，使得

（5）将归一化好的结点特征和车流量数据矩阵S输入到第一层GCN层。

（6）引入注意力机制，计算结点v与邻居结点vi之间的权重系数eiv。

（7）对所有的权重系数做softmax归一化处理，得到最终权重系数αiv=softmax(eiv)。

（8）选择加和聚合算子Aggsum。

（9）通过第一层GCN 层聚合操作后聚合了一阶邻居结点的特征。

（10）第一层输出经过relu变换输入到第二层，再执行一遍（6）～（8），此时聚合了二阶邻居结点特征

（11）第二层输出经过relu变换输入到第三层GRU层，第三层输出后输入到第四层GRU层。

（12）最后一层Dense层的输入为第四层的输出，得出预测结果。

结合该算法的每一层参数配置如表2所示。

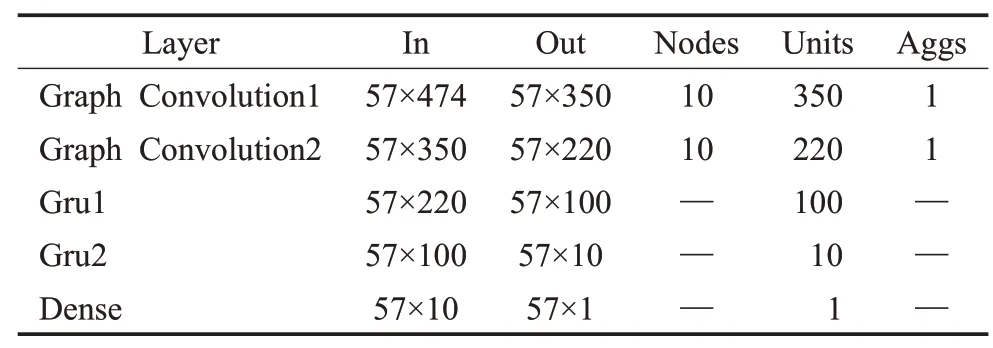
表2 模型参数配置

4.2 误差评价指标

为了评价模型的预测性能，本文分别以均方误差（Mean Square Error，MSE）以及准确率（ACC）作为评价指标，定义如下所示：

式中，N为样本个数，yn为车流量真实值，为车流量预测结果。

4.3 实验结果及分析

本实验在RTX2060 上采用Adam 优化器来对模型进行优化，学习速率为0.001，训练批次为200次，权重衰减为5E−4。为了消除不同数量级对模型训练带来影响，需要在读取数据之后对所有数据首先进行归一化处理，同时也能够有效提升模型的训练速度，降低计算资源的消耗。归一化方法：

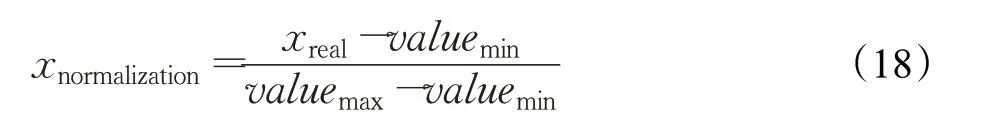
根据表3 实验结果发现本文模型预测性能最优，MSE 为0.000 53，相较于GCN+LSTM 提高了0.000 16，相当于将每一个预测值与真实值之间的差距平均缩小了约0.095 5；相较于GCN提高了0.010 7，预测值与真实值之间的差距平均缩小了约0.781 0；相较于GRU 和LSTM分别提高了0.010 4和0.011 0，差距也分别缩小了约0.769 9、0.791 8，说明本文模型具有较高的稳定性。而准确率随着模型复杂度降低成正比，因此也验证了组合时空特征提取模型在预测过程中优于独立特征提取模型，并且本实验模型的准确率高于其他非GCN 模型达8%左右，证明图卷积神经网络在预测不规则排列数据时相比其他模型能力较强，在车流量预测中可以达到很好的预测效果。

表3 5种模型的预测结果

如图9～11 所示，随着训练次数的增加本实验模型在训练集和验证集上都表现出了较快的收敛速度，且3 个图中GRU 模型收敛速度明显快于LSTM 模型，证明了本实验模型训练速度优于其他模型并且GRU 模型计算速度快于LSTM 模型。使用该预测模型预测第11 天上午8：30 时刻的57 条路段车流量，并与真实值对比。

图9 5种模型损失变化情况

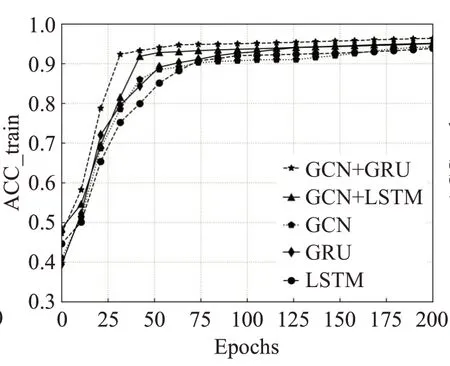
图10 5种模型在训练集上准确率变化情况

图11 5种模型在验证集上准确率变化情况

观察图12～16，可以看出在图12中预测模型的拟合度较高，其他模型在编号为10～24 以及36～38 的路段上拟合度较差，波动较大，为了便于观察，将5种模型的整体差值范围表示如图17所示。

图12 GCN+GRU模型预测结果与真实值比较

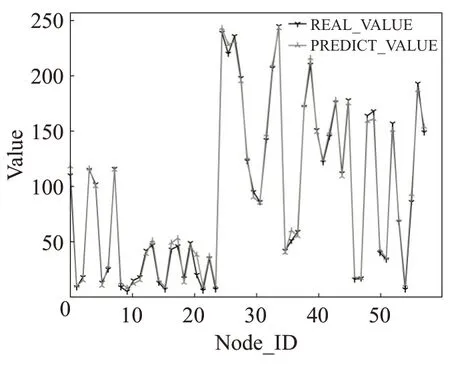
图13 GCN+LSTM模型预测结果与真实值对比

图14 GCN模型预测结果与真实值比较

图15 GRU模型预测结果与真实值比较

图16 LSTM模型预测结果与真实值比较

图17 5种模型预测差值

图17 中不同颜色代表不同路段上的差值，可以看出所提模型的差值最低，LSTM 模型的差值最高，进一步验证了所提组合模型的精度要优于其他模型。

5 结束语

图神经网络在处理矢量数据的优势使其可以在城市路网中有效地提取路网中的空间相关性，门控循环单元在有效处理时间序列数据的同时在计算速度上相比于LSTM模型也有所提高，二者组合共同预测城市市区内57 条道路的车流量，并且在实验中证明该模型在训练速度以及预测精度上均明显优于其他非图神经网络以及非组合的模型。虽然模型性能不错，但是考虑到在大量的数据下神经网络可以表现出更好的性能，因此为了提升模型的性能，在未来的工作中将会采集更多的数据给模型增强数据驱动的能力。