纯相位全息图优化算法

卜浩祯， 焦述铭

(1. 纽约大学 数学系，纽约10003；2. 鹏城实验室，深圳 518055)

1 引 言

三维立体显示技术在近年来得到了飞速发展，其在娱乐、医学、研究、军事等领域的应用也层出不穷，如视觉研究、医学成像、科学可视化、虚拟原型展示、防伪水印等[1-3]。目前有多种可以实现三维显示的技术，如基于显示屏的虚拟现实技术以及基于双目视差的立体显示技术等。然而相比于现实场景，以上显示技术都存在一定的成像瑕疵。其中一个重要原因是人眼观看显示图像时的辐辏距离(Vergence Distance)与聚焦距离(Focal Distance)不匹配所导致的视觉辐辏调节冲突(Vergence-Accommodation Conflict)，会引起观看者的不适、眩晕及视疲劳等问题[4-7]。

1947年由Gabor发明的全息成像技术是一种运用光的干涉与衍射来对光场波前进行记录与重建的技术[8]。“全息”意为“全部的信息”，指该技术会记录原光场的所有振幅及相位信息，并能完全重建物体和场景的波前信息[9-10]。相比于传统的三维成像技术，全息成像中的信息载体全息图包含了物体的全部形状和深度信息，被认为是三维场景重建的终极最佳方法[11-19]。得益于硬件设施的进步，计算机生成全息图技术作为全息成像技术的一个子领域在近几年得到快速的发展。不同于传统的全息成像技术，计算机生成全息图技术不需要专门的全息记录材料，而是利用空间光调制器加载由计算机生成的全息图[20]。正因如此，该技术带来了对波前信息前所未有的灵活控制能力，也可以生成并非真实存在的物体的全息图[21-25]。

在目前的计算机生成全息图领域中，空间光调制器的种类有微机电系统调制器(Microelectromechanical Systems Spatial Light Modulators)[26-28]与液晶空间光调制器(Liquid-Crystal Spatial Light Modulators)[29- 31]等，其中液晶空间光调制器为目前主流的设备，能够提供理想的相位调制能力。由于在实际应用中，绝大多数可用的空间光调制设备只能有效地调制光波的相位或者振幅之一[32]，因此需要生成的全息图只包含相位信息或振幅信息，而不能是两者皆有[33]。使用两个空间光调制器分别调制振幅与相位是一个可行的解决办法，但是这种方法的实验装置十分复杂且昂贵[34-35]。另外，由于使用空间光调制器会让全息图衍射为三部分：物体像、共轭物体像以及零阶(Object Image，Conjugate Object Image，and Zero Order)，大大降低了衍射效率，且由于相较于纯振幅空间光调制器，纯相位空间光调制器拥有理论上的更高衍射效率，因此纯相位全息图是当前计算机生成全息图的主流编码方式[36-39]。然而，这种纯相位的编码使得对于全息图生成问题，并不存在一个简单准确的直接解，而是要通过近似去取得最优解[40]；而且由于空间光调制器的分辨率及其每个像素点调制取值范围的限制，全息图在加载时也需要进行离散化与量化，所以找出量化误差最小的最优数值近似也是全息图计算问题之一[41]。

过去的几十年间，计算机生成纯相位全息图算法层出不穷，其核心就是纯相位全息图优化问题：给定一个复振幅全息图(Complex-Amplitude Hologram)，将其编码成为一个纯相位全息图(Phase-Only Hologram)，使得用该纯相位全息图进行光学重建所得到的图像要尽可能还原原始图像。这些方法主要分为3类：迭代方法、非迭代方法与其他方法。迭代算法通常由一个对目标全息图的近似出发，经过一系列的重复操作不断优化这个近似全息图，直到该近似所得到的重建图像满足一定的误差要求；非迭代算法不需要重复的大量优化计算，会根据指定步骤一次性给出近似解。由于较低的计算负荷，非迭代算法更符合实时全息显示的要求，而代价是这类方法的重建质量不如迭代算法；其他方法种类繁多，各有特点。本文将总结目前主要的纯相位全息图生成的迭代方法、非迭代方法以及其他方法。

2 迭代性算法

2.1 Gerchberg-Saxton类算法

在计算机生成全息显示场景中，给定任意二维或三维图像，首先利用计算机生成全息图算法在全息图平面生成一幅全息图[42-44]，再利用空间光调制器加载这幅全息图，之后通过激光照射，在全息图上发生衍射形成衍射图案，便可以在重建图像平面对原始图像进行光学重建(图1)。

图1 计算机生成全息图的重建Fig.1 Reconstruction of a computer-generated hologram

可以生成纯相位全息图的迭代算法中，迭代傅立叶变换算法(Iterative Fourier Transform Algorithm)是一种比较具有代表性的算法，该类算法的特点是通过傅立叶变换在两个平面中的反复传递[45-49]。迭代傅立叶变换算法，或称误差减少算法(Error Reduction Algorithm)在20世纪70年代早期被作为数字全息的一种算法而提出，后来被Gerchberg与Saxton修改并运用在相位提取领域，成为了迭代算法中最著名也可能是被运用最多的方法——Gerchberg-Saxton(GS)算法[50]。该算法中，根据全息图平面与重建图像平面的振幅分布，通过迭代进行正逆向的光波传递以及施加在两个平面上的限制条件(Constraint)，进而求得全息图平面中光场的相位信息(图2)。该方法在计算纯相位全息图场景中十分适用，可以使用菲涅尔变换或者傅立叶变换来进行光场传播的计算。以用傅立叶变换的GS算法为例，首先对相位分布进行一个估计φ(0)，之后算法的每次迭代包含以下步骤：

图2 Gerchberg-Saxton算法流程图Fig.2 Flowchart of Gerchberg-Saxton algorithm

(1)

(2)限制条件：以所要求的对象光场振幅分布替换第一步中传递至图像重建平面的光场的振幅分布:

(2)

Atarget为目标图像振幅。

(3)计算第二步中光场由物体图像平面至全息图平面的传递:

(3)

(4)限制条件：将第三步中传递至全息图平面的光场振幅设为单位1，得到纯相位全息图P(n+1)

(4)

P(n+1)=exp(iφ(n+1)).

(5)

在GS算法的基础上有很多改进版本[51-52]。加权GS算法(Gerchberg-Saxton Algorithm with Weight Coefficients)会先进行数轮GS算法迭代，之后会将重建图像平面中的限制条件替换为目标图像的振幅乘以一个分数形式的权重系数[53]，然后继续运算直到满足一定的误差条件。以原始图像与重建图像间的归一化标准差(NSTD)作为评判标准，加权GS算法比GS算法取得了一定程度的提升[54-55]，且收敛速率会有所提高。然而，加权GS算法有时会出现无法收敛的问题，而自适应加权GS方法(Adaptive Weighted GS Method)用指数形式的权重系数替代分数形式的权重系数可以更好地解决收敛性问题[56]。此外，基于并行结构的相位恢复算法会以多个初始值为起点进行并行运算来对GS算法进行加速，因此在收敛速率方面与针对灰阶图像的重建质量方面也有提高[57]。GS算法也被改进为一系列迭代映射算法，如连续GS算法(Sequential GS Method)[58]，也称菲涅尔乒乓算法(Fresnel Ping-Pong Algorithm)[59]，以及全局GS算法(Global GS Method)[60]，这两种算法可被用于计算能够进行多深度平面图像重建的纯相位全息图。此外，GS算法还被改进为可以用于处理倾斜空间光调制器(Tilted SLM)的算法[61]以及用于处理三维对象的算法[62-64]。

在GS算法的基础之上，Fienup提出了Fienup算法以提高算法的收敛速率[65]，该方法与GS算法类似，只是在重建图像平面上的限制条件有所不同，不再是将该平面上的光波振幅直接限制为目标图像振幅，而是设为上次迭代结果与原始图像振幅的一个函数与上次迭代结果之和。在Fienup算法基础上，研究者还提出自适应加法算法(Adaptive-Additive Method)，该方法在重建图像平面上的限制条件是将振幅分布设为原始图像与上次迭代结果的线性组合。相较于GS算法与GSW算法，Fienup算法与AA算法的重建图像可以取得更高的准确度，收敛速率也更快，但是所需的计算资源也会更多一些[54](表1)。

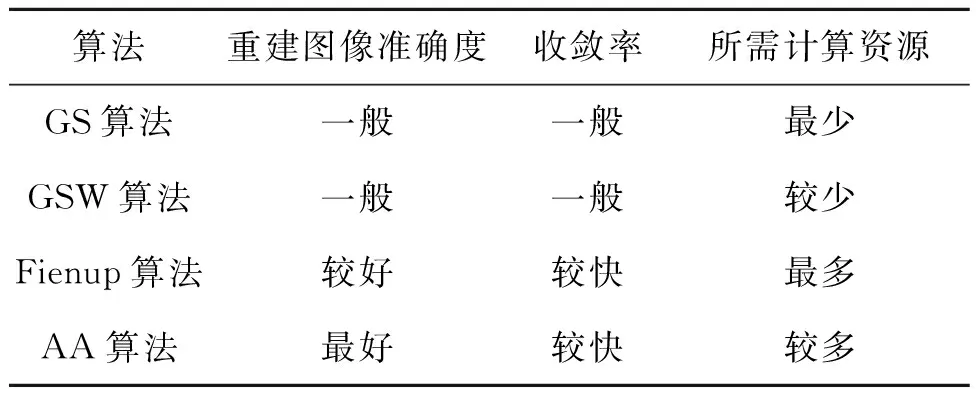
表1 GS算法、GSW算法、Fienup算法与AA算法比较

在GS算法中，初始条件的设定对于算法收敛速度和结果质量有至关重要的影响，因此以往不少研究针对迭代初始条件进行了优化[66-75]。通常，这些算法会在原始图像之上加一层随机相位来使其光场变得分散，避免在全息图上过度聚集，但是这种方法又会带来斑点噪声。为了消除斑点噪声，有些方法会使用非随机相位如二次、线性、常数或锥形相位作为迭代时的初始相位，另一些方法基于物体图像适应性设计初始相位[46]。近些年，出现了使用了双限制(Double Constraints)进行斑点噪声去除的GS算法[76-79]，这种方法在菲涅尔衍射区域可以取得很好的重建结果，而由Pang改进的采用了基于对象的二次相位(Object-Dependent Quadratic Phase Distribution)的迭代算法可以在远场衍射区域取得很好的噪声消除效果[80]。此外，还有一些结合了其他优化技术的GS迭代算法，比如在最初几次迭代中用直方图(Histogram)调整图像替代约束条件的直方图补偿算法(Histogram Compensation Algorithm)，该方法可以增强全息图对过亮或过暗像素点的重建质量[81]；其他例子包括运用了自定成本函数与非凸优化的三维全息图生成算法[82]，运用了最速下降与加权的混合类GS算法(Hybrid Gerchberg-Saxton-like Algorithm)[83]，可以对重建图像进行缩放的方法[84]，运用了压缩感知理论的傅立叶全息图计算方法[85]，针对圆柱形全息图进行斑点噪声减少的自衍射算法(Self-Diffraction Method)[86]，以及运用了基于自动控制PID原理的误差跟踪控制减少算法(Error Tracking-Control-Reduction Algorithm)来提高衍射效率，并减少量化误差与斑点噪声的算法[87]。

2.2 误差扩散算法

误差扩散算法(Error Diffusion Method)是另一种类型的迭代算法，该算法是在全息图平面的各个像素之间依次迭代，而不是在全息图平面与物体图像平面间迭代[88-95]。误差扩散算法与GS类算法的第二个不同在于误差扩散算法不需要物体图像的任何信息，只需要复振幅全息图本身，便可直接在其上操作并计算出一个纯相位全息图。

该方法原理：当复振幅全息图的振幅信息被直接移除时，每个像素点都会产生误差，

E(ui,vj)=H(ui,vj)-P(ui,vj)，

(6)

其中：H(ui,vj)为点(ui,vj)的复振幅像素值，P(ui,vj)为该点舍弃振幅信息后的纯相位像素值，E(ui,vj)为所产生的误差。而误差扩散算法将逐行从左向右依次扫描每个像素点，并将每个像素点的误差按照一定的比重向尚未扫描到的像素点扩散(图3(a))。双向误差扩散算法的奇数行与偶数行的扫描方向是相反的(图3(b))，这种双向扫描方式会抵消部分由单向扫描所带来的相关性误差，进而取得更高的重建准确度[96](图4)。通常，误差扩散方法中的权重参数是经验性地按照Floyd-Steinberg系数设置的[97]，然而在一些问题上这样的权重设置并非最优解。双系数误差扩散在抑制斑点噪声方面取得了不错的提高[98]，另外由Yang改进地运用了遗传算法的误差扩散方法，其权重参数可以根据不同的全息图自适应性地调整，在重建准确度上取得了进一步的提高[99]。由周婷婷改进的结合了分层角谱算法的误差扩散算法可以生成三维对象的纯相位全息图，即首先利用分层角谱算法计算三维物体的复振幅光场，再利用误差扩散算法计算纯相位全息图，取得了不错的重建质量[100]。近期，Liu提出的方法在误差公式中的第二项前加入了一个调制因子，使得振幅信息被移除时所带来的误差可以针对不同图像适应性地调整。通过找到最佳调制因子，该方法可以提高纯相位全息图的重建质量[101]。

图3 (a)误差从左向右扫描扩散；(b)误差与从右向左扫描的扩散。Fig.3 (a)Error diffusion from left to right; (b) Error diffusion from right to left.

图4 利用双向误差扩散方法进行纯相位全息图生成及仿真全息图像重建。(a)原始图像；(b)重建图像。Fig.4 Generation of phase-only hologram and simulated reconstruction using bi-directional error diffusion. (a) Original image; (b) Reconstructed image.

3 非迭代性算法

3.1 随机相位方法

相较于迭代算法，非迭代算法的特点是无需任何优化过程、仅用一步计算得到所要的全息图，正因如此，非迭代算法的运算速度更快、更符合实时显示的需求，但是其重建图像的质量通常不如迭代算法。最简单直接的一种纯相位全息图生成方法是振幅信息移除(Direct Amplitude Truncation)，即直接移除由原始图像生成的复全息图中的振幅部分，然而这种方法会导致极大的误差。同时，由于纯相位全息图实际上是一种高频滤波器，重建图像只是原始图像的边界与线条部分[102]。因此需要引入随机相位掩膜(Random Phase Mask)使原始图像的波前分散至整幅全息图以提高重建质量[103-108]，如一步相位提取方法(One-Step Phase retrieval)中，在生成全息图之前会先在原图像前加一个随机相位掩膜，之后仅保留该全息图的相位部分用以重建图像[109-110]。该方法很快速，但是重建图像的线条和边缘参差不齐，而且随机相位掩膜的使用又会导致斑点噪声的产生[111]。

图5显示了随机相位在纯相位全息图重建中的作用。图5(a)是原始图像；图5(b)是不使用随机相位的重建场景，其中黄色平面代表原始图像，该平面发出的光场夹角很小，很难被全息图记录到，因此下面的重建图像中很难看清原始图像的轮廓；图5(c)显示的是使用随机相位的重建场景，由于叠加了随机相位，原始图像平面发出的光场得以分散，重建图像质量也有了很大提升，然而随之而来的斑点噪声也十分明显。为了减少这种斑点噪声，近期有一种新的随机相位方法，该方法会针对不同的图像，引入具有不同频率的随机相位掩膜以进一步减少信息损失、提高重建质量[112]。

图5 随机相位对纯相位全息图重建结果的作用示例。(a)原始图像；(b)未添加随机相位掩膜；(c)添加随机相位掩膜。Fig.5 Effect of using random phase on reconstruction of phase-only hologram. (a)Original image; (b)Reconstruction without random phase; (c) Reconstruction with random phase.

3.2 采样类方法

除了随机相位掩膜方法以外，还有很多可以用于减少斑点噪声的非迭代方法，如采用下采样的采样纯相位全息图(Sampled-Phase-only Hologram)方法[113-116]，该方法首先会以一个均匀网格对物体的振幅分布进行下采样，然后生成复全息图的相位值将被保留作为纯相位全息图。该方法可以保证重建图像的质量，但下采样过程本身会造成原物体图像的信息损失，导致一定程度的质量减损。该下采样掩膜的部分如图6所示，其中黑色点表示的是采样点，白色点表示的是非采样点。

图6 下采样点示意图Fig.6 Illustration of down-sampling

另一种采样方法是互补纯相位全息图(Complementary phase-only hologram)[117]，该方法通过在两个不同的下采样网格中快速切换，可以进一步提高重建质量，然而该方法使得计算量翻倍，且对SLM切换全息图的速度有很高的要求。该方法的互补采样点如图7所示，左侧的两幅采样点图可以合成为等式右侧的采样点图，其中黑点为采样点，白点为非采样点。类似采用SLM高速切换显示不同全息图来进行图像重建的方法还有时分复用方法(Time-Division Multiplexing

图7 互补采样点示意图Fig.7 Illustration of complementary sampling

Method)[118-121]，然而这类方法都需要高性能的SLM，因此在动态实时全息显示的场景下并不十分适用。此外，还可以采用自适应性下采样掩膜(Adaptive Down-Sampling Mask)，该方法会在图片中的平缓区域进行稀疏采样，而在图像边界等快速变化的区域进行密集采样[122]。

3.3 模式化掩膜与二次相位掩膜方法

模式化相位掩膜(Patterned Phase-Only Hologram)方法可以在有限计算量下提高重建质量[123]，该方法在原始图像上填加了一层由一致的相位模式区块(Phase Pattern Block)拼接而成的相位掩膜，这种重复拼接的相位掩膜会使光场振幅趋于均匀。由于原始图像中均匀分布的每个局部区域都被加上了相同的相位模式，重建图像中将呈现出有规律的像素化噪声。还有一些非迭代方法会采用二次相位掩膜(Quadratic Phase)与快速傅立叶变换，由于没有使用随机相位掩膜，该类方法可以取得较低的斑点噪声与较高的峰值信号噪声比(PSNR)[124-126]。

3.4 双相位方法

其他能够减少斑点噪声的非迭代纯相位全息图生成算法还有双相位方法(Double-Phase Method)[127-134]。该方法首先将原始图像的振幅信息编码为两个纯相位值，然后使用两个棋盘形状的互补二元滤波器将这两个相位分布组合为一个纯相位全息图[135]，之后通过闪耀光栅来将未被衍射光波从重建图像中分离出去，以达到减少噪声的目的[136]。然而，采用二维棋盘状函数会导致能量的大量损失[137]，而采用一维光栅函数编码则能大幅提高一级衍射分量所携带的能量[138]。另一种减少噪声的方法是通过使用带宽限制函数(Band-Limiting Function)的双相位算法，带宽限制函数可以有效地移除复振幅双相位化时产生的噪声[139]。

3.5 非随机相位方法

为了减少斑点噪声，不使用随机相位掩膜的方法(Random Phase-Free Method)也有很多[140-145]。该方法旨在用可控的相位处理光波，如同心球面波(Spherical Concentric Wave)，替代随机相位掩膜，这种收敛的光波可以将原始图像的光波均匀地扩散至整幅全息图，然而这种方法更适用于纯振幅全息图，若用于生成纯相位全息图则需要与误差扩散算法结合[146]。

4 其他算法

4.1 直接算法

除了迭代算法与非迭代算法，有一种直接算法可以用于计算纯相位全息图。假设纯相位全息图有M×N个像素，每个像素点的相位值有Q种可能取值，则纯相位全息图生成问题的搜索空间为M×N×Q，目标是找到重建图像与原始图像误差最小的全息图所有像素值。直接算法主要有3类：直接搜索算法(Direct Search Algorithm)、模拟退火算法(Simulated Annealing Algorithm)以及遗传算法(Genetic Algorithm)。

直接搜索算法会随机选取一个全息图像素点，然后改变其相位值，若改变后得全息图重建准确度更高则保留，否则放弃这次改变。这种方法十分简单易操作，然而它所计算出的结果只是局部最优解[147-151]。模拟退火算法采用的是随机搜索办法，该方法计算量大且耗时很长，但是其优点是可以得到接近全局最优解的结果[152-153]。遗传算法采用了全局搜索(Crossover)和局部搜索(Mutation)，需要极大的储存空间，而该方法的优点是它可以与其他算法很好地结合，并且是一种并行算法[154-156]。这3种方法的优缺点总结如表2所示。直接算法相比于迭代法和非迭代法，总体上计算成本明显更高。

表2 三种直接算法的比较Tab.2 Comparison of three direct methods

4.2 迭代与非迭代结合类算法

还有一种新的纯相位全息图生成算法于近年被提出，该类方法处于迭代算法与非迭代算法两种分类之间。2018年，Alejandro提出了一种简单有效的算法，该算法利用传统的GS迭代，首先针对一个光学系统的分辨率、像素点尺寸以及对象尺寸去计算出该系统一个最优化的相位掩膜(Optimized Random Phase，ORAP)，之后再用该系统与其对应的最优化掩膜去计算其他任意对象图像的纯相位全息图而不再需要迭代[157]。相较于GS算法，该算法的缺陷在于需要知道对象图像的尺寸及分辨率信息，然而该方法节省了大量的计算时间，同时保持着较高的重建准确度，因此十分适合全息电影或动态实时显示等应用。

在该方法的基础之上，Alejandro将其改进为可以生成三维场景全息图的算法。首先，通过菲涅尔迭代算法计算出一个最优随机相位板(Optimized Random Phase Tile)，之后，该随机相位板将会像在模式化相位掩膜方法(PPOH)中一样被拼接成一个掩膜，用于生成全息图。该方法相比于ORAP方法与PPOH方法可以取得更高的重建质量，并且可以减少斑点噪声以及周期性的模式化噪声[158]。

由Alejandro提出的这类算法通常会先迭代性地计算出一个最优相位掩膜，然后再用非迭代算法去生成全息图[125,159-160]。该类方法后续产生了许多衍生算法，比如非迭代多平面全息图算法(Noniterative Multiplane Hologram)会使用一步连续GS算法(One-Step Sequential GS Method)和一个混合相位及复限制条件(Mixed Phase and Complex Constraint)，该限制条件含有一个参数C，经过实验会得到一个最优的C值[161-162]，之后可以用这个C的取值进行迭代计算。最终结果显示该类结合迭代与非迭代的方法在衍射平面数目较多时，在部分平面上可以取得比传统的迭代性连续GS算法更好的重建质量，同时该类方法会具有更快的收敛速率以及更高的衍射效率[40]。

4.3 基于深度学习的计算全息算法

近年来快速发展的深度学习方法也被用于全息图压缩[163,164]以及生成全息图[165-166]。Horisaki于2018年提出的基于深度学习的纯相位全息图生成算法，使得光场反向传递过程可以由计算生成的斑点数据集回归而得出[167]。由Lee等提出的训练方法在数据集中混入特定几何形状，可以极大地提高所生成复振幅全息图的质量[168]。由Eybposh等人提出的DeepCGH方法可以用训练出来的卷积神经网络生成一个复振幅全息图可行解，之后再对该可行解的光场反向传递进行模拟来计算出全息图平面的纯相位全息图[169]。2020年，由Khan等提出的GAN-HOLO运用了生成对抗网络，取得了不错的实验结果[170]；另外由Peng等人提出了一个高质量实时计算机生成纯相位全息图算法，该算法基于最速下降法(Steepest-Gradient-Descent Method)，并且运用了Camera-In-The-Loop(CITL)技术。在每次循环中，CITL技术可以直接捕捉到全息图的光学而非数字模拟重建结果，并且将该结果用于对全息图的进一步优化；另外，该算法可以训练得出一个光场传递的可解释模型，在此基础之上训练出的HoloNet深度学习模型可以做到全彩、高质量、高分辨率的实时二维全息显示[171]。由Horisaki等人提出的基于卷积神经网络方法所生成的全息图可以进行多个平面的图像重建，对特定种类的三维图像能够取得较高的重建质量[172]。

4.4 基于Wirtinger Flow的相位提取方法

Chakravarthy等人提出的基于维尔丁格流(Wirtinger Flow)的相位提取方法可以将相位提取问题转化为可用一阶优化算法(First-Order Optimization Method)进行优化的二次问题(Quadratic Problem)。该方法可以灵活地使用各种成本函数，包括由深度神经网络训练出的感知损失，并且也可以与随机优化方法结合。运用该相位提取方法进行全息图优化可以使重建质量达到极高的准确度，而计算成本则仅与GS算法相当，并且在进行底层代码以及硬件优化之后，有望实现实时全息显示[173]。

5 结 论

本文以迭代性算法、非迭代性算法以及其他算法作为分类，总结了计算机生成纯相位全息图的主要算法。以Gerchberg-Saxton为代表的迭代性算法的特点是利用傅立叶变换或菲涅尔变换在两个平面间多次变换，并辅以灵活度极高的限制条件，可以取得很好的重建图像准确度。在Gerchberg-Saxton基础之上的一系列改进的迭代算法拥有更高的灵活性，可以更好地消除斑点噪声并取得更高的重建质量，而付出的代价是更高的计算负荷。作为另一种迭代性方法，误差扩散方法所需的计算量会更小一些，而且无需原始图像的信息便可以直接由复振幅全息图生成纯相位全息图，并能取得不错的重建质量，权重参数也给这种方法一定的自由度与提升空间；此外，误差扩散方法与其他算法的结合适用性很强，可以与各种各样的相位掩膜方法结合使用。

作为非迭代性算法，非随机相位方法、采样方法以及双相位方法都能很好地减少斑点噪声，而且计算负荷也很小，十分符合实时全息显示的需求。

其他类的方法中，直接算法需要极大的运算量与储存空间，因此这些方法在实际应用中并不十分常见。而近年提出的作为迭代算法和非迭代算法的结合类算法，则既能在较小的计算量下通过迭代方法算出一个最优相位掩膜，再用这个掩膜去快速地计算出纯相位全息图，同时也能保证较高的重建质量和较高的收敛速率，也十分符合动态实时显示场景的要求。基于深度学习的全息图生成方法也在几年来不断取得突破，CITL技术的引入也使得全息图优化过程中的光学重建结果可以更有效地与深度学习或者最速梯度下降等方法结合，以取得更高的重建质量。另外，深度学习方法可以在固定的计算复杂度内生成高质量的纯相位全息图，并且可以灵活地设定自定义优化目标。最后，基于维尔丁格流的全息图优化方法既可以用与传统GS算法相当的计算量将重建误差减少一个量级，还可以灵活使用不同的成本函数，并且能与各类一阶优化算法结合，具有很大的发展潜力。

目前，传统的迭代与非迭代的纯相位全息图优化算法都已经取得了不错的效果，但需要在计算耗时与重建质量间做出取舍，深度学习、维尔丁格流等新方法的不断出现为解决这一问题带来了新的思路，这些工作都有利于实时、广视场、高质量全息三维显示的早日实现。现有不少算法主要针对由二维物体图像生成的平面纯相位全息图，而由三维物体图像生成曲面纯相位全息图(如柱面全息图和球面全息图)的优化算法值得进一步研究，此外面向数字微镜器件(DMD)等振幅型空间光调制器的全息图优化算法[174-175]还相对偏少，可以借鉴各种纯相位全息图的优化算法进行进一步探索。