基于机翼颤振风洞试验模型的地面颤振模拟试验验证
2021-07-14宋巧治王彬文李晓东
宋巧治,王彬文,李晓东
(中国飞机强度研究所,陕西 西安 710065)
1 引 言
颤振是一种气动弹性不稳定现象,会直接影响飞行器的飞行安全。目前,防止颤振的主要途径是获得颤振边界并设定一定的安全裕度,并以此设计飞行器的飞行包线。地面颤振模拟试验是近年来提出的一种新的颤振测试验证技术,该技术通过重构飞行器的非定常气动力并以激振器的离散力进行模拟施加,实现颤振地面模拟与测试并获得颤振边界,此方法在试验件的安全性、试验周期、成本等方面具有一定的优势。
早在1962年,美国John Hopkins大学应用物理实验室的Kearns研究了地面单点激励颤振模拟技术[1]。1974年,法国的Rajagopal在其博士论文中研究了二自由度舵面模型的地面颤振模拟[2],但是由于缺乏先进的数字计算机技术、成熟的非定常气动力降阶技术以及多输入多输出系统控制技术,无法实现分布非定常气动力模拟,因此地面颤振模拟只能成为一个设想。随着非定常气动力数字计算机技术的进步、非定常气动力模型降阶技术研究及多输入多输出控制理论的发展,地面颤振模拟技术的理念再次受到关注。
2010年5月,美国J Zeng等完成了地面颤振模拟试验的原理性研究和实验室验证试验,并在实验室内实现了矩形平板翼的地面颤振模拟[3]。2007年,俄罗斯的中央空气流体力学研究院(TsAGI)的Karkle等提出了气动弹性的电动机械模拟方法(EMM),实现了真实结构水平尾翼的颤振地面模拟验证,同时对导弹的气动伺服弹性、操纵面非线性气动弹性特性进行了预测[4]。
潘树祥和齐丕骞于上世纪80年代在国内率先研究了地面颤振模拟技术,进行热颤振边界的预测及验证,对该技术进行了初步探索[5]。吴志刚等在非定常气动力重构技术、气动力模拟加载控制等领域进行了研究[6-9]。宋巧治等建立了简单的GFT试验系统,在实验室进行了平板机翼的地面颤振试验技术研究,利用4个激振器模拟非定常气动力,取得了较好的效果[10]。邵崇晖针对壁板极限环运动开展了地面颤振模拟试验技术研究[11]。胡巍等对地面颤振中带有操纵面的结构气动力重构方法进行了研究[12]。
本文对地面颤振模拟试验系统中涉及到的非定常气动力重构、受结构影响的激振器激励力控制方法进行了研究,设计了降低激振器及顶杆附加影响的装置,建立了地面颤振模拟试验系统,并以风洞试验模型开展试验,对地面颤振模拟试验系统进行精度分析及验证。
2 结构颤振特性分析
为了对模型进行气动力模型重构,首先需要对结构和气动力进行建模和分析。为此建立了结构的有限元模型,主承力结构以梁单元模拟,对结构模型进行了分区,对每个分区的质量及惯量进行了分析和评估。在此基础上,建立了有限元模型,并进行了结构振动特性分析及结构振动特性试验,测试了结构前4阶模态的频率、振型和阻尼特性。利用模态试验结果对有限元模型进行了修正,图1为结构有限元模型,表1给出了修正后有限元结果及模态试验测试结果的对比,两者吻合很好(相对误差在3%以内),可以用于后续的颤振分析。
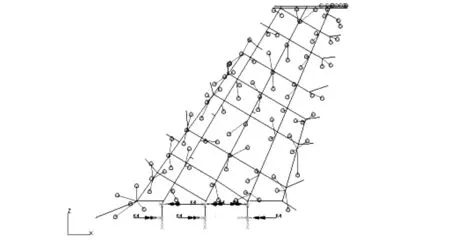
图1 结构有限元模型

表1 有限元仿真结果相对误差
划分了气动网格,建立了样条插值方法,对结构的颤振特性进行了分析,获得了结构的颤振边界,并与风洞测试结果进行了对比分析。图2为本文中使用的气动网格,图3为计算获得的v-g曲线和v-f曲线。
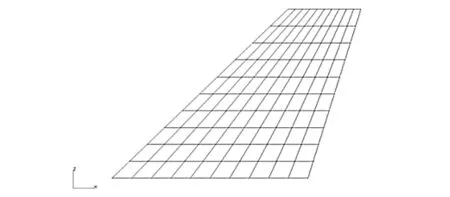
图2 结构气动网格划分
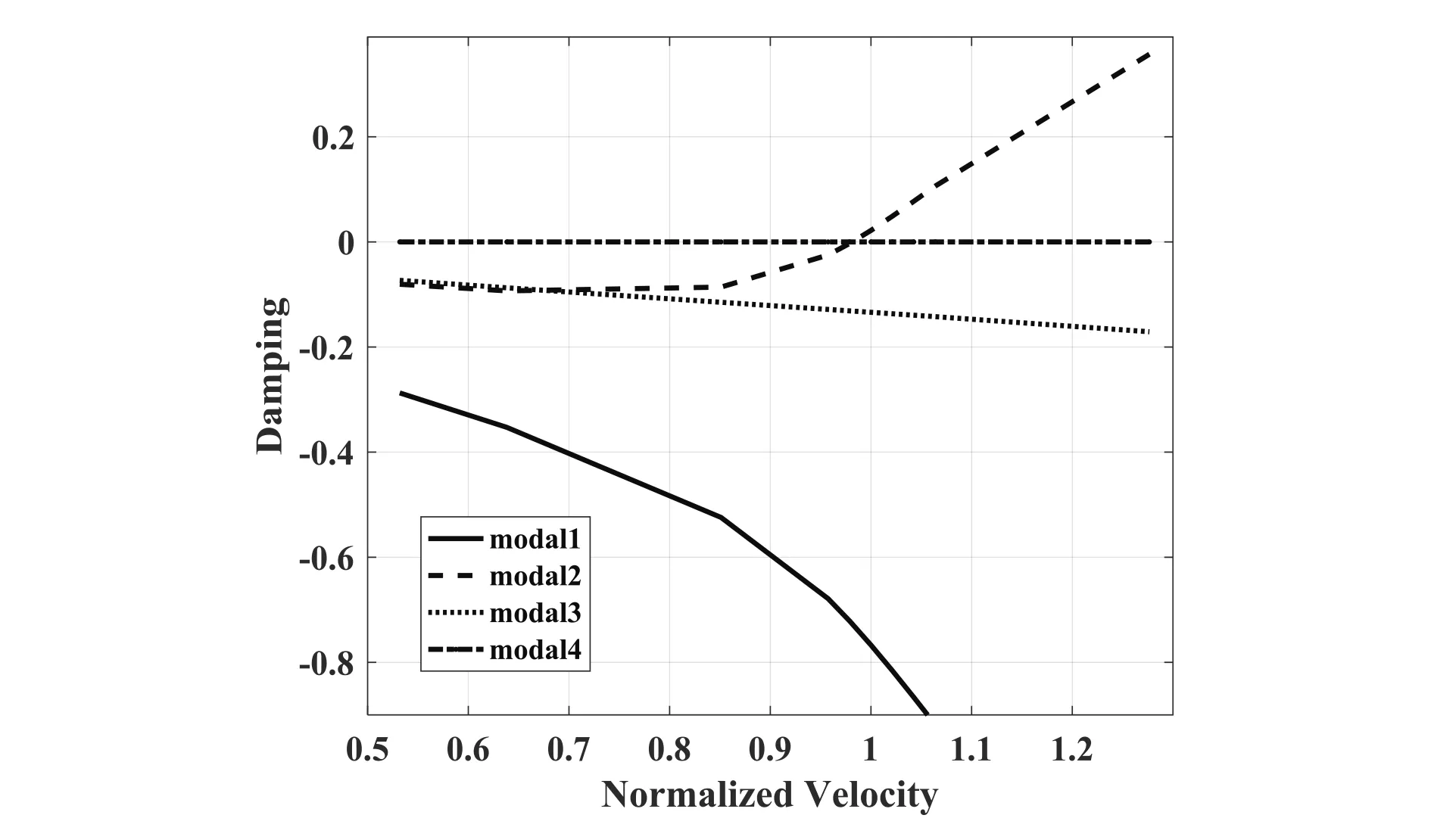
(a)颤振v-g曲线
3 非定常气动力重构
气动弹性系统的运动方程可写为:
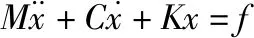
(1)
在式(1)中引入广义坐标q,则有:
x=Φq
(2)
式中,Φ为结构模态矩阵,代入式(1)并前乘ΦT可得:
(3)
式中,Φa为气动节点的模态列阵;fa为气动节点的气动力,对其进行整理,变形为:
(4)
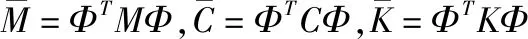
假设减缩后的激振点和拾振点组成的节点集合为s,则减缩后对应的气动弹性方程变为:
(5)
对比式(4)和式(5)可以发现,方程的左边项两者一致,即结构的方程不变。若要保证颤振分析结果的一致性,则需要保证方程的右端项一致,即:
(6)
式中,Δ为等效气动力与真实气动力之间的误差。
利用插值矩阵,根据范数相容性原理可得:
(7)
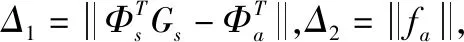
观察Δ1,对其内部进行矩阵转置,仍满足:
(8)
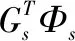
激励点/拾振点的选取,可以通过一定的优化方法实现。优化设计变量为一定数目的离散点,优化目标为系统的气动节点模态振型。频域颤振分析时,各阶模态振型对于系统颤振的贡献量并不相同,定义对颤振贡献量较大的模态为颤振关键模态,优化时对其取较高的关注度。综上对激励点/拾振点的优化目标重新修正,定义为颤振关键模态的振型最优,可记为:
(9)
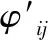
在基于广义力等效的过程中,采用降阶前后结构模态振型在气动网格上插值振型的绝对误差作为优化目标函数,优化变量为激振点的位置(对应每个激振点布置一个拾振点),通过遗传算法进行优化分析。图4给出了优化过程中,优化目标函数值的变化曲线。优化过程中每一代个体数量确定为20个,总计50代,通过优化获得了激振点的位置。优化过程中目标函数不断减小,证明插值后振型与原模型插值振型相似度明显提高。图5为优化后激振点的位置。
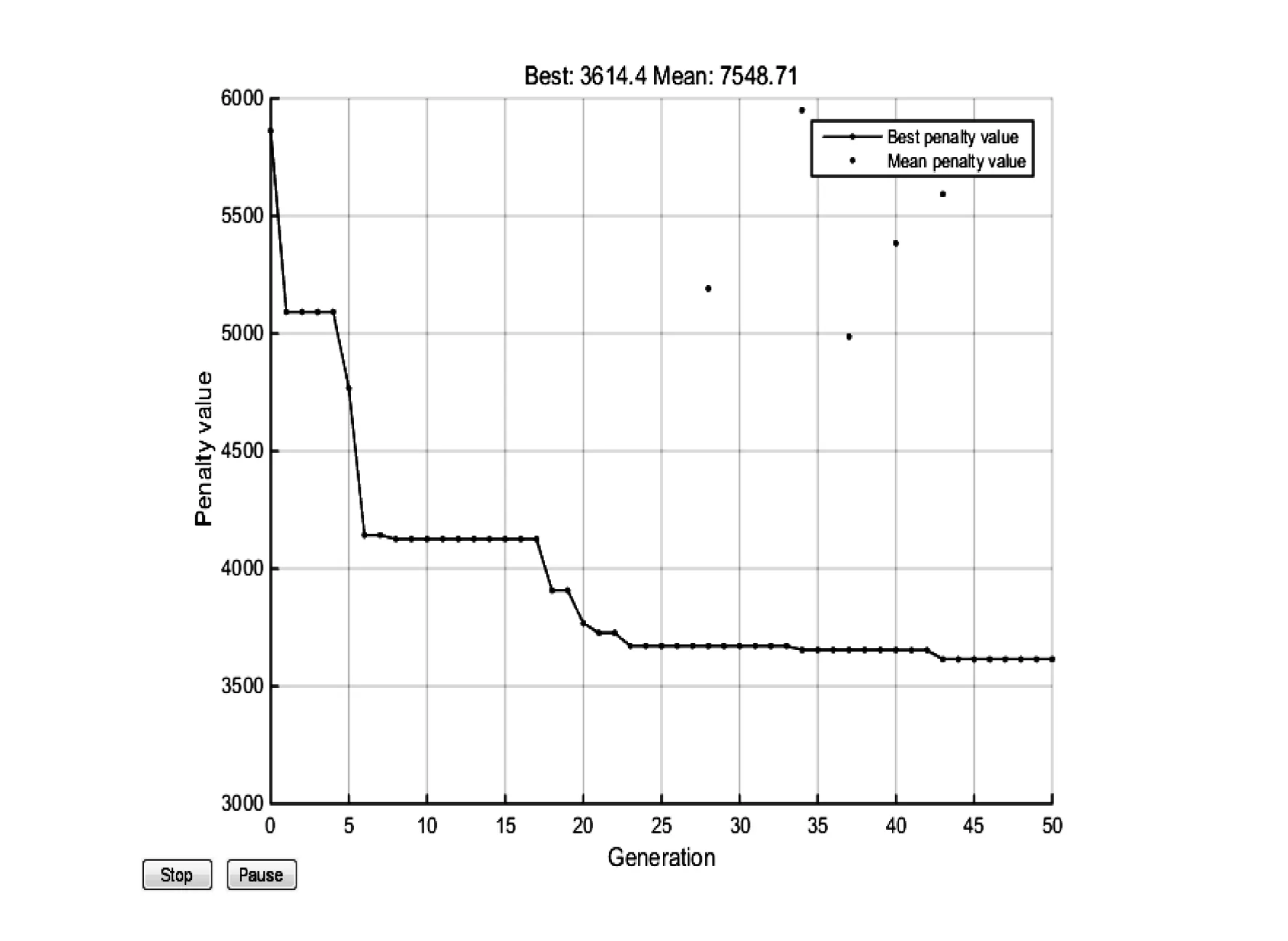
图4 优化目标函数的变化曲线
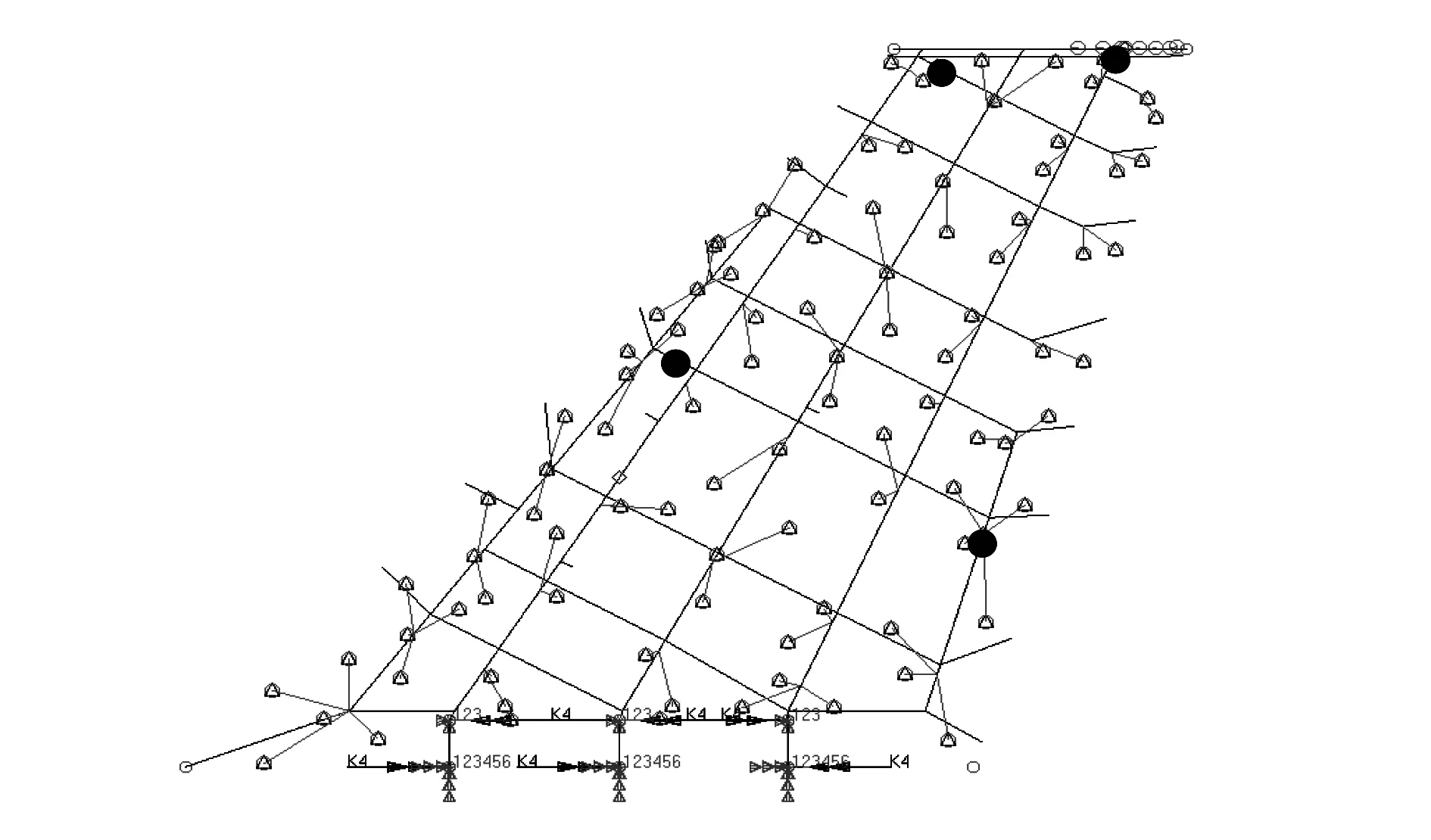
图5 优化后激振点的位置分布
图6给出了插值点优化后系统颤振v-g曲线和v-f曲线,可以看出,两者一致性很好,证明所选择的插值点构成的新的颤振系统能够代表原系统的颤振特性。
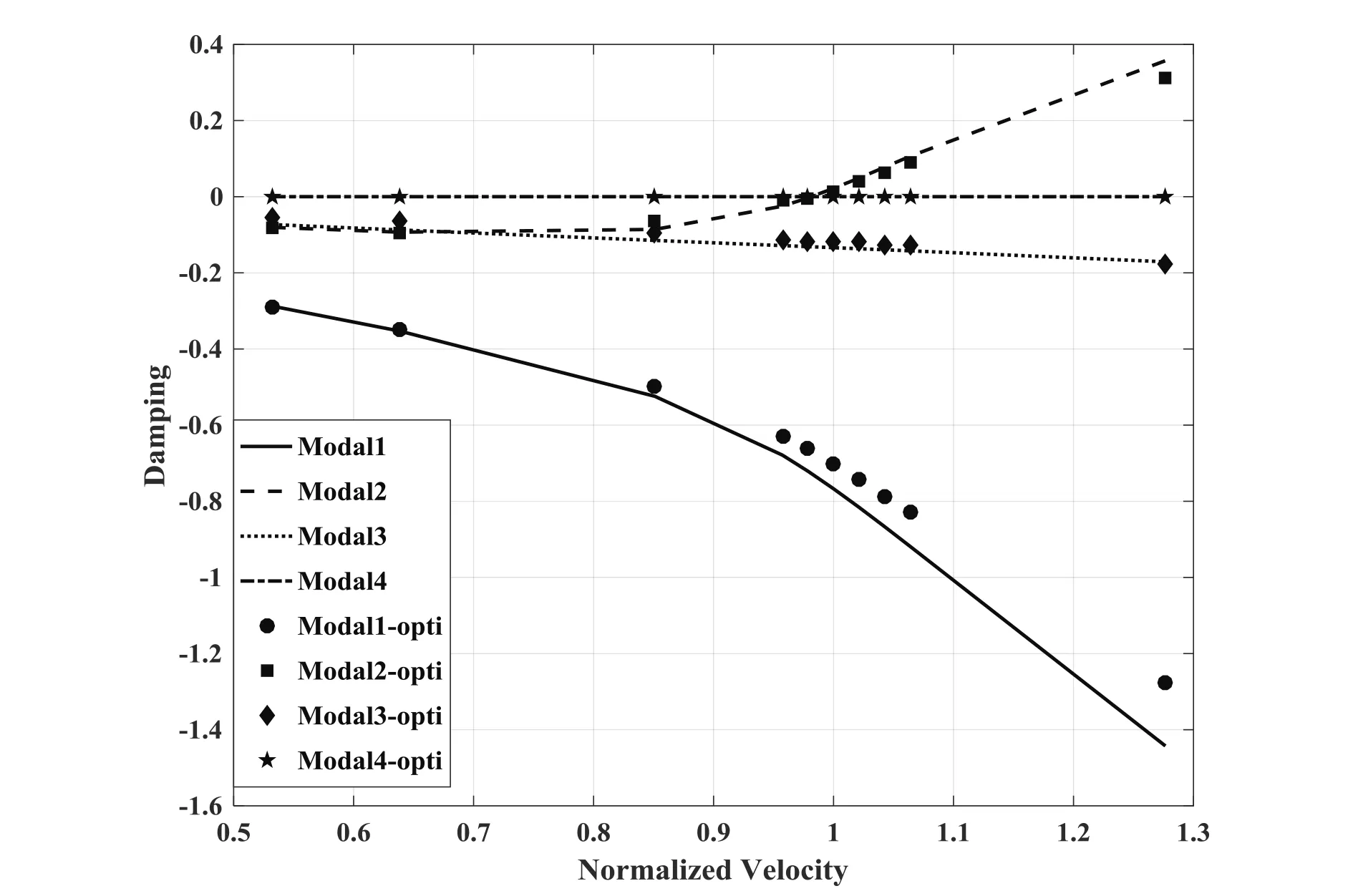
(a)v-g曲线
为了在后续试验中使用气动力模型,需要对气动力模型进行时域拟合(即有理函数拟合)。本次采用最小状态法对频域气动力进行拟合,最小状态法采用式(10)对气动力进行有理函数拟合。
(10)
计算过程中,首先获取在各个减缩频率下的气动力影响系数矩阵,通过有理函数拟合获取气动力模型矩阵,建立气动力状态空间模型。图7为气动力影响系数矩阵有理拟合情况,圆圈为频域气动力影响系数,星号为时域气动力影响系数,可以看出两者吻合很好。
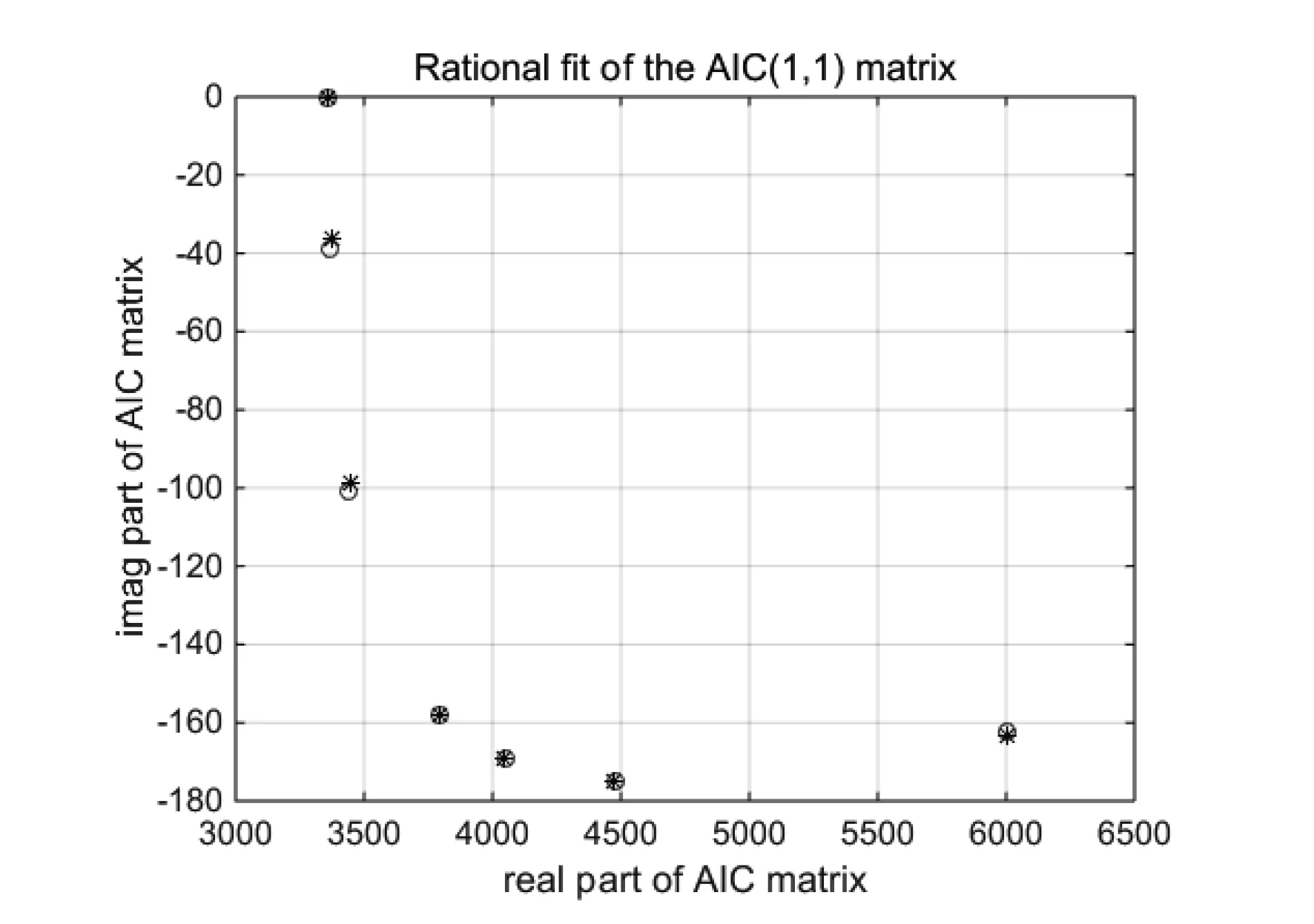
图7 气动力影响系数矩阵有理拟合结果
4 激励力加载控制
为了保证对气动力的精确模拟,本文采用反馈控制的方法对输出进行精确控制。同时,为了避免激振器等众多环节中的不确定性对控制器性能的影响,采用鲁棒控制算法进行控制器设计。进行控制器设计,首先建立了被控系统的状态空间模型。系统建模采用试验建模方式,建模方法采用子空间方法,其中确定性系统的状态空间描述如式(11)所示[13]。
(11)
子空间辨识方法首先构建输入和输出的Hankle矩阵,然后利用斜投影以及奇异值分解方法获得系统可观测矩阵以及系统状态矩阵,系统的状态量可由上述两个矩阵求得。
(12)
(13)
(14)
(15)
(16)
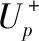
为了对系统的输出力进行控制,采用H∞鲁棒控制算法,标准H∞控制框图如图8所示。同时,为了简化控制器设计,采用混合灵敏度设计方法进行设计。混合灵敏度方法的难点在于加权矩阵的确定[14],本文采用如下方式进行定义。
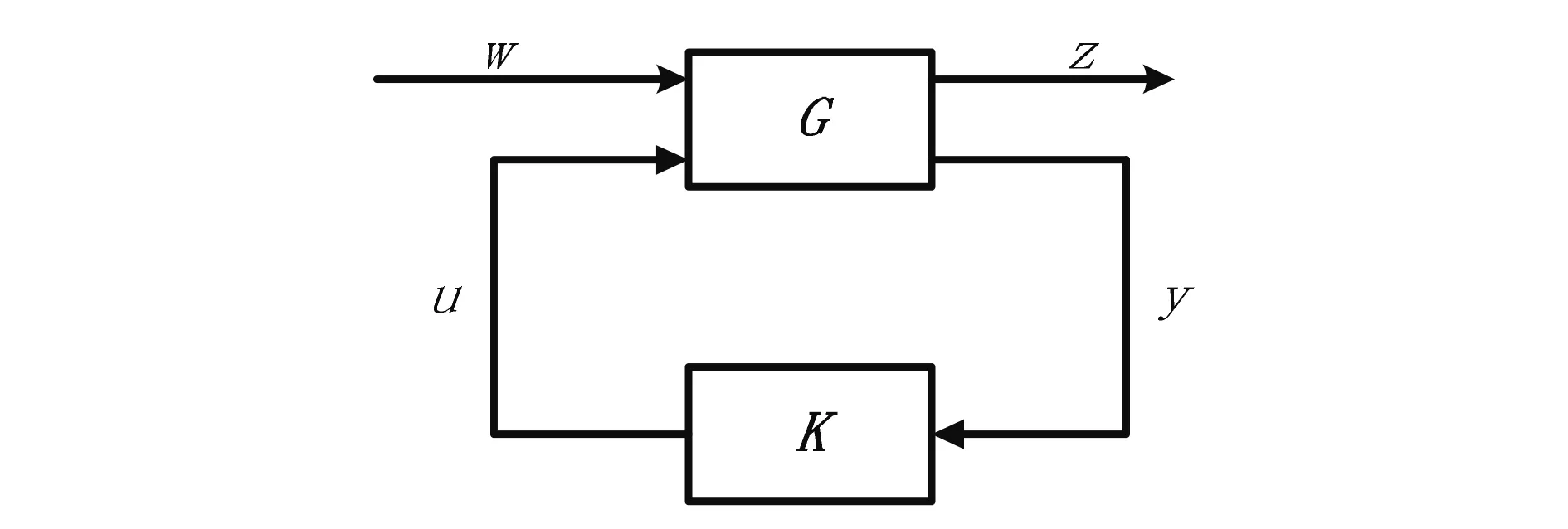
图8 标准H∞控制框图
Wp为系统的性能加权函数矩阵,代表了干扰的频谱特性,反映了对系统的灵敏度函数S的形状要求。通常Wp在控制器设定的工作范围内幅值较大,在工作频段范围外幅值较小,以保证控制器的鲁棒性。由于颤振临界状态附近响应为单频信号,采用ButterWorth带通滤波器,滤波器的带通频率包含颤振频率,滤波器的频率响应特性见图9。
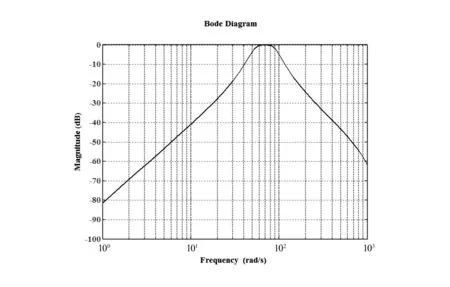
图9 权矩阵Wp频响特性
Wu加权函数矩阵用于对控制器的输出控制电压幅值进行控制,防止出现电压过高引起执行机构过饱和现象,通常选择较大的静态增益。
Wr为系统的鲁棒性加权函数矩阵,由模型的非结构不确定性即高频未建模动态特性和模型参数不确定性所决定。依据本文定义的系统不确定性及其物理含义,Wr选为3阶对角阵,以系统不确定度的近似上界作为Wr,权矩阵和系统不确定度频响特性如图10所示。
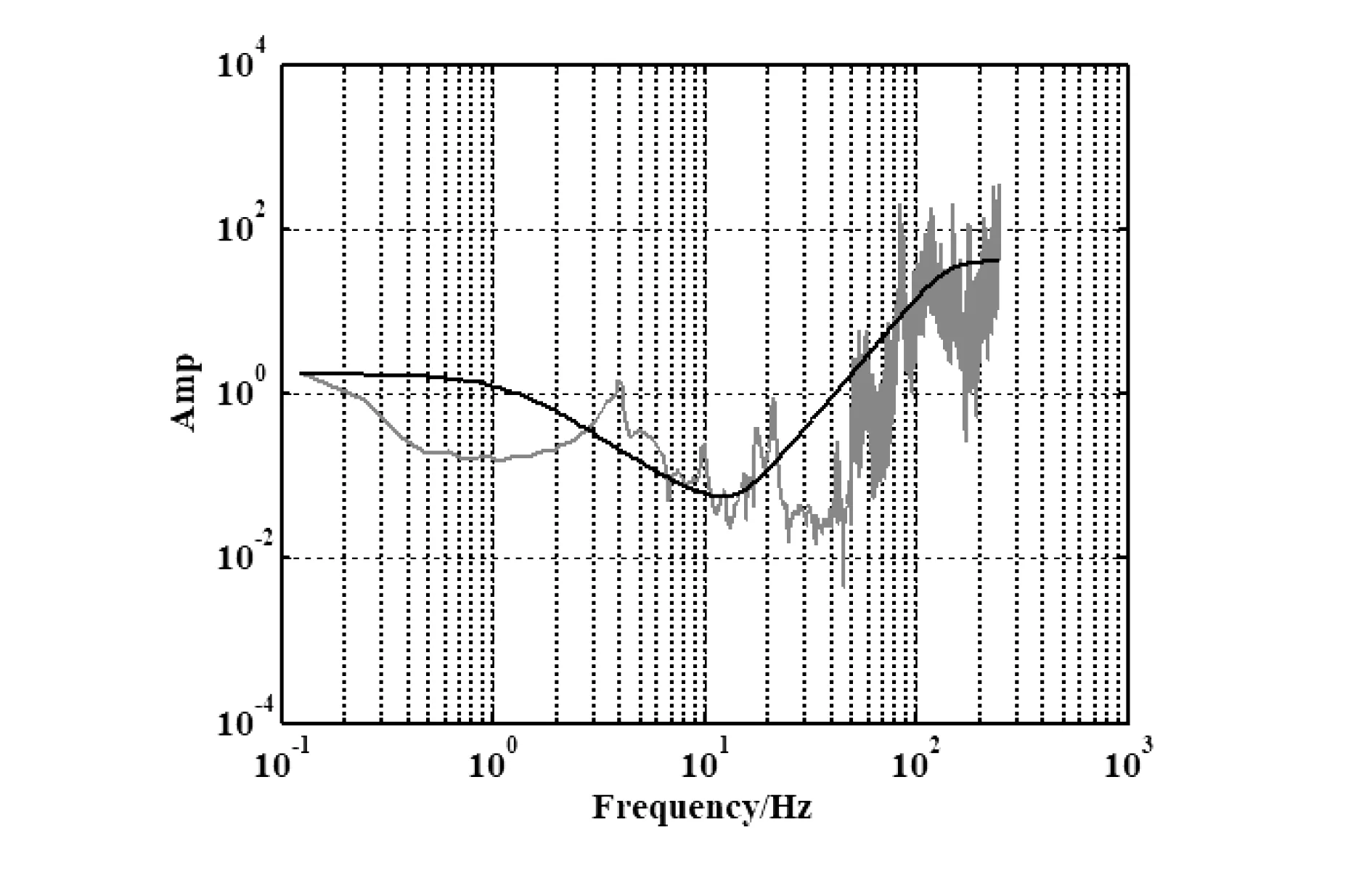
图10 权矩阵Wr与系统不确定度关系
5 地面颤振验证试验
在建立气动力模型和控制器模型的基础上构建了地面颤振模拟试验系统, 并在不同风速条件下进行了系统响应测试与分析。 通过响应的收敛和发散情况对结构的颤振边界进行判断,利用二分法进行测试速度的调节,直至结构响应达到等幅值振荡时, 可认为结构达到了颤振临界点, 此时对应的测试速度和响应的频率为结构的颤振临界速度和频率。在超临界状态下,结构的响应幅值是发散的。当响应达到设定的阀值时,试验终止。
对结构进行了地面颤振试验测试,获得了结构的颤振边界,但是测试获得的颤振速度误差较大(14%)。通过分析可知,颤振速度误差的主要来源在于激振器的附加刚度对结构的动态特性乃至颤振特性的影响。由于在地面颤振模拟试验中,已对结构主运动方向的力进行监测和控制,因此该方向的附加特性影响可忽略不计。但是由于力传感器仅测试轴向力,侧向力以及力矩特性无法进行测试,而模型的刚度较低,侧向力和力矩的影响会对结构的颤振特性产生一定影响。图11给出了激振器顶杆附加力矩对结构振动影响的示意图。
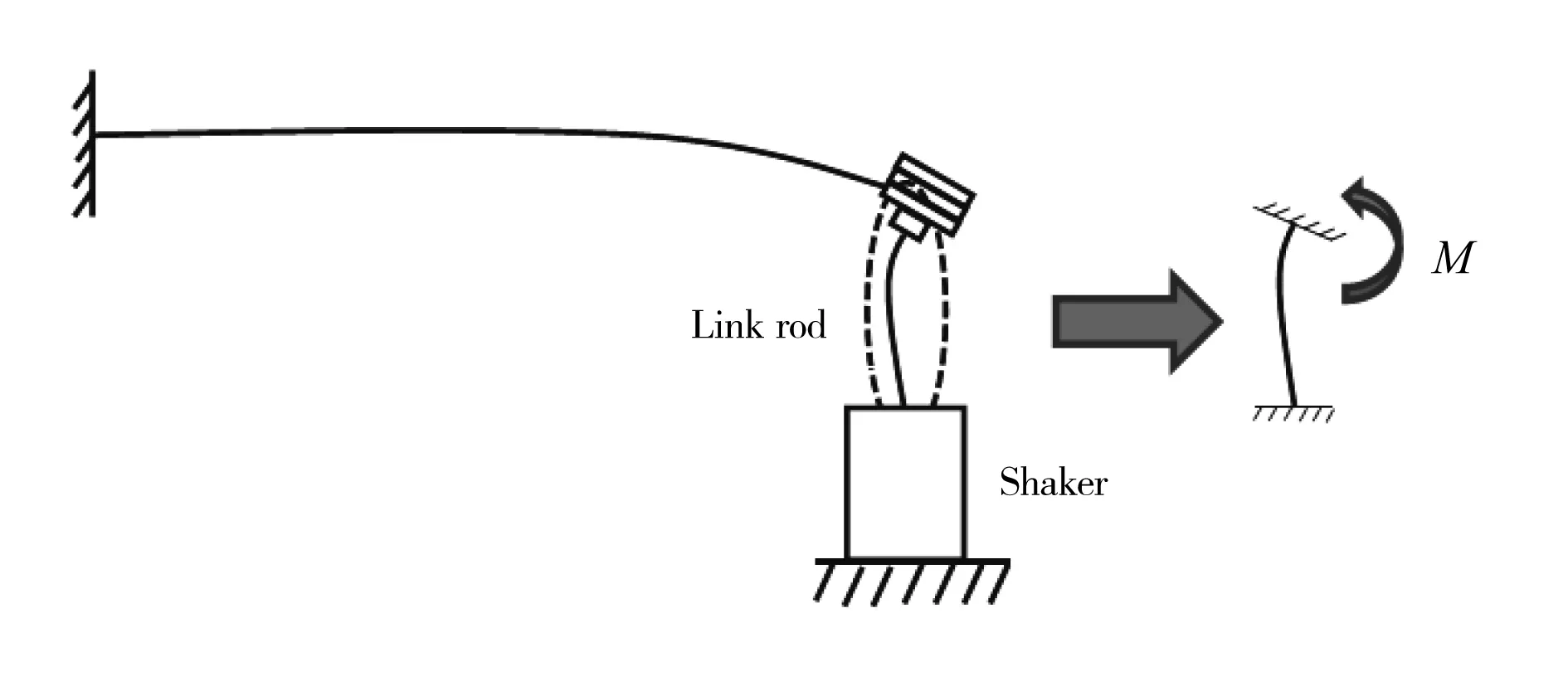
图11 激振器附加刚度对结构动态特性影响
为了尽量消除激振器附加刚度的影响,设计了一种降低附加力矩作用的激振器顶杆装置,并用于地面颤振模拟试验系统。图12为提出的降低激振器顶杆附加力矩效果的方案,该方案通过在顶杆顶端安装球头绞的方式,避免了力矩向结构传递,从而降低顶杆的影响。
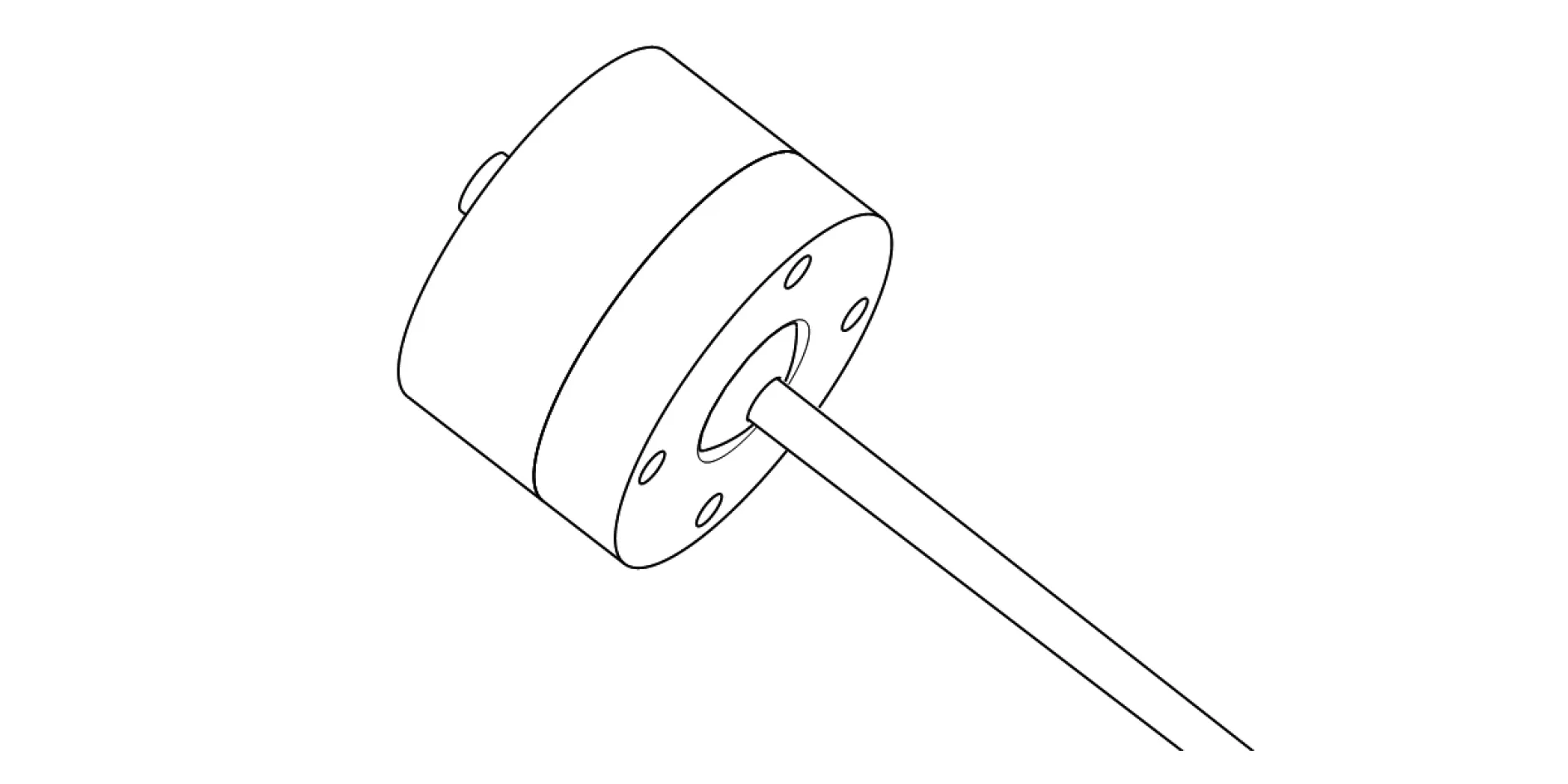
图12 降低附加力矩作用的顶杆
对结构的颤振特性进行了进一步测试,获得了颤振边界。表2给出了分析、风洞试验及地面颤振模拟试验的测试结果,可以看出,地面颤振模拟试验与风洞试验结果相比误差较小,颤振速度误差为6.2%,在工程可接受范围内,证明了方案的可行性。
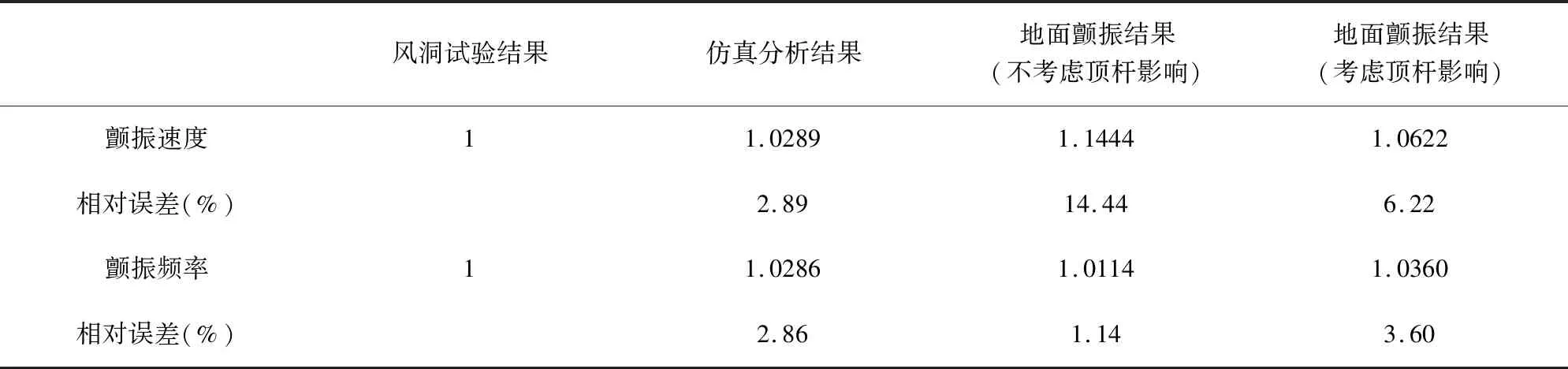
表2 地面颤振模拟试验结果与风洞结果对比
图13为不同测试状态下的结构响应,可以看出,在临界状态下,结构响应幅值不随时间变化,可近似看作等幅振荡,该点对应的测试速度即为颤振临界速度。图14为临界点处的结构响应频谱,从中可以读取结构响应的主频率成分,该主频率即为颤振频率。图15给出了临界条件下力的跟踪效果,可以看出,激励力与重构气动力基本一致,可认为气动力准确施加在结构上。
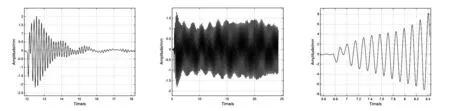
(a) 亚临界状态 (b) 临界状态 (c)超临界状态图13 地面颤振模拟试验结果
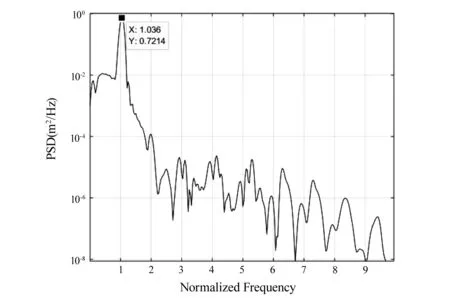
图14 颤振临界点处结构响应功率谱密度
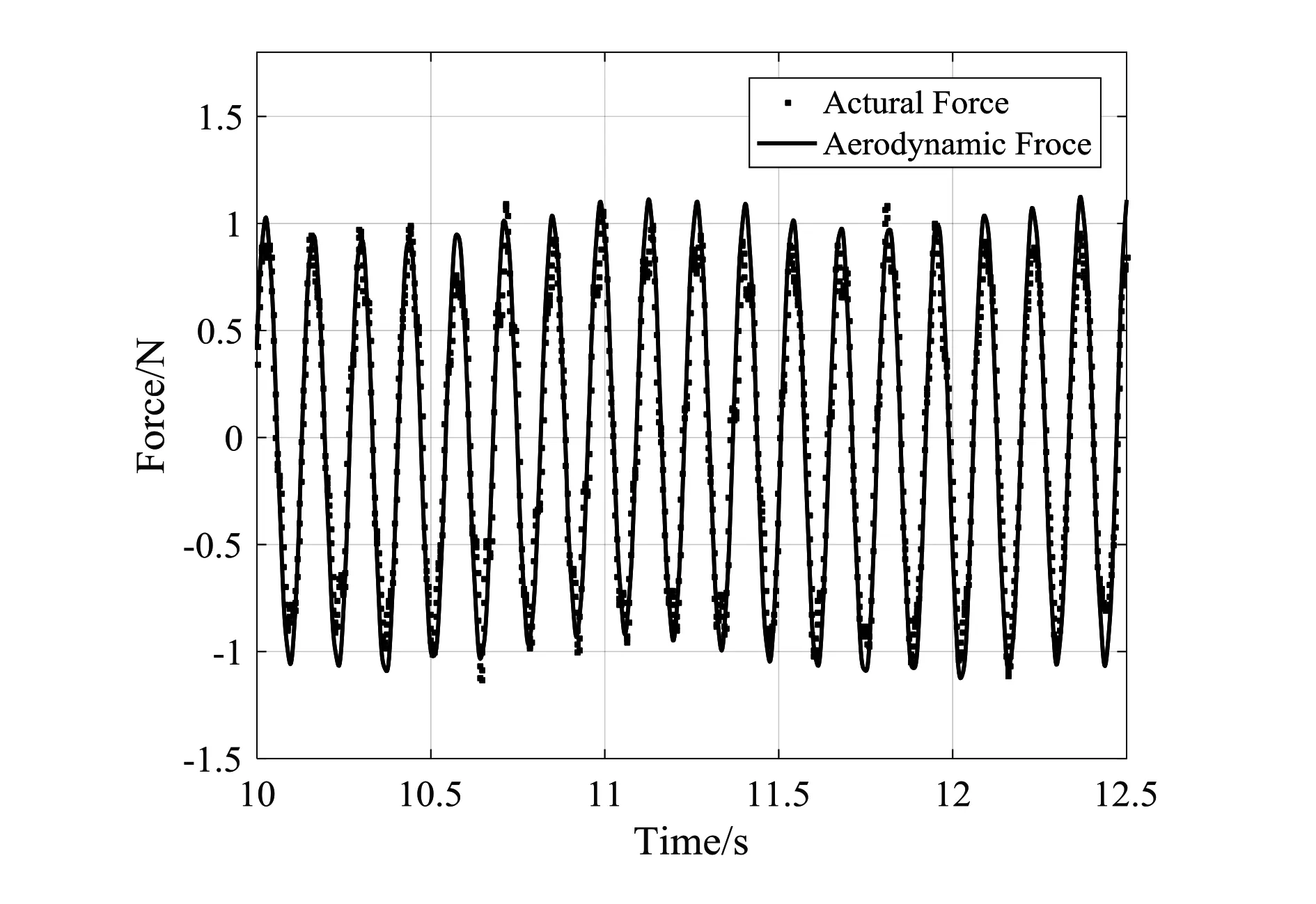
图15 颤振临界状态力控制效果
6 结 论
通过将地面颤振模拟试验测试结果与分析及风洞试验结果进行对比,可以得出以下结论:
(1)地面颤振模拟试验系统可以较为准确地测试结构的颤振边界,测试结果满足工程精度要求;
(2)影响地面颤振模拟试验系统测试精度的主要因素为非定常气动力重构精度,为了提升试验精度,需要研究基于计算流体力学或者风洞试验的非定常气动力建模方法;
(3)激振器以及顶杆对柔性结构的振动特性影响较大,因此在试验过程中必须予以考虑,并尽量降低其影响以降低对颤振边界测试的影响。
