双边初级永磁型游标直线电动机优化设计

2021-07-14杜怿,尹雯

江苏大学学报（自然科学版） 2021年4期

杜怿, 尹雯

(江苏大学电气信息工程学院, 江苏镇江 212013)

直线电动机无需机械传动部件即可直接提供直线推力，故采用直线电动机的直线驱动系统具有结构简单可靠、运行效率高等优点[1-3].文献[4]提出了一种新型双边初级永磁型游标直线(double-sided linear primary permanent magnet vernier, DSLPPMV)电动机，该电动机电枢绕组和永磁体均位于短初级上，而次级仅为设有凸极的铁心，且基于磁场调制原理运行，因此该电动机不仅具有次级结构简单、机械强度高、便于永磁体冷却等优势，还具备低速、大推力等优点，适合诸如电梯驱动等长行程工况.此外，与传统的单边初级永磁游标直线电动机[5]相比，DSLPPMV电动机初级无轭部铁心，降低了电动机初级的质量，从而可以改善系统的动态性能，且降低电动机制造成本.采用双侧平板式结构，可以抵消初级单边磁拉力，降低对滑轨的要求，其模块化结构也可以提供高容错能力.

基于有限元的逐点扫描，可以实现对电动机的高精度优化，但该方法存在计算量庞大、数据处理困难、耗时长等问题，而这些问题将随着电动机结构复杂程度的增加而更为凸出.响应面法(response surface method, RSM)是一种统计和数学技术，用于寻找所研究物理系统的最佳拟合响应[6-8].近年来，将其与有限元等数值模拟方法相结合，已被公认为是电气工程研究的一种有效方法.在RSM中，通常建立拟合回归模型来表示优化目标与设计变量之间的关系.在该模型中，所研究的优化目标是设计变量所表示的函数.这与单纯使用有限元法相比，设计优化过程都更容易，省时省力.因此选择采用RSM方法对DSLPPMV电动机进行优化设计，以满足大推力、高效率的设计要求.

针对电动机的优化设计，笔者分析电动机本身以及产品需求，选取几个优化目标，对电动机模型进行分析，并结合综合敏感度计算以确定优化参数.结合有限元仿真法以及响应面法对电动机进行多目标优化，进行样机试验以验证该优化方法的有效性.

1 电动机结构与运行原理

1.1 DSLPPMV电动机结构

6/2极DSLPPMV电动机的结构如图1所示.

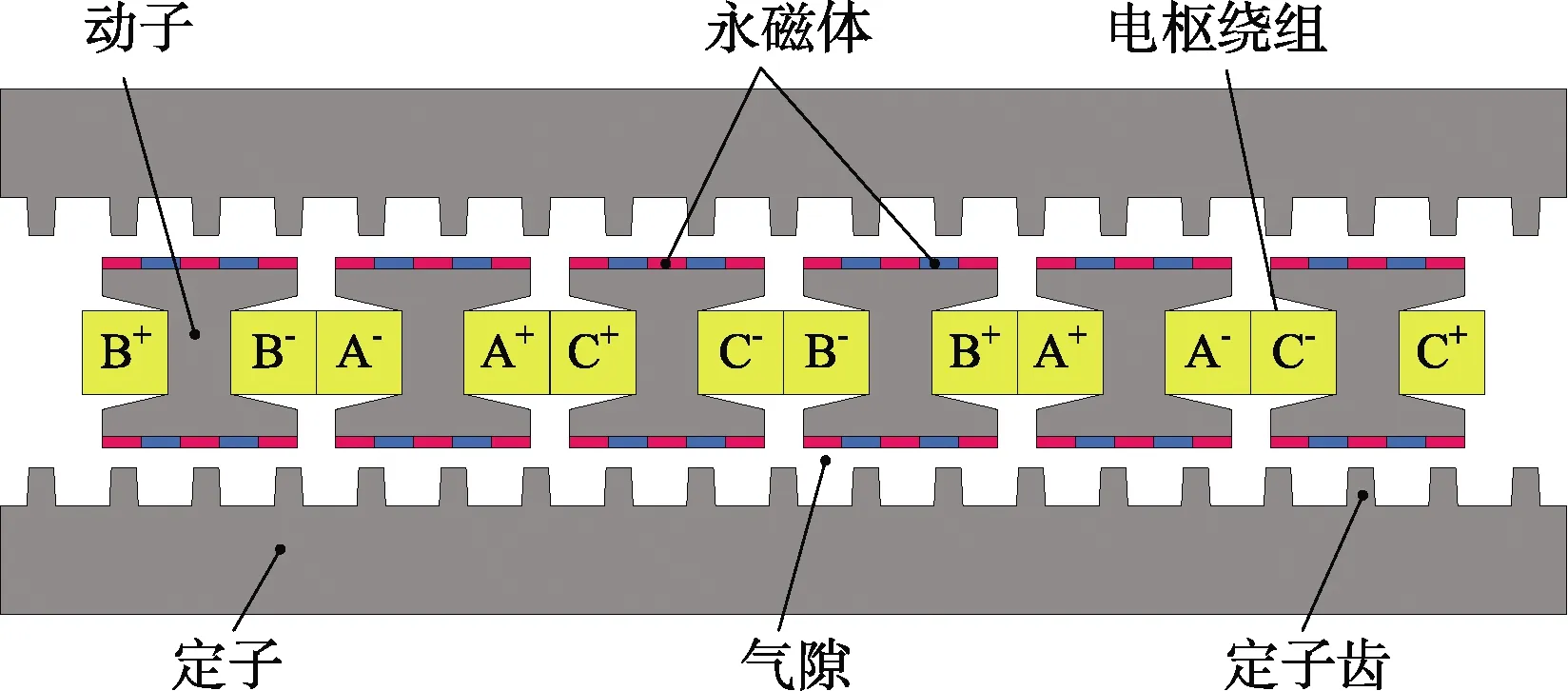
图1 DSLPPMV电动机结构示意图

电动机采用双侧平板结构，为典型的短初级长次级结构，电枢绕组和永磁体都位于短初级上，次级仅由带有凸极齿的硅钢片叠压而成.

初级齿为I型，均匀分散排列，形成初级部分的齿槽结构.永磁体贴装于初级齿表面，每个初级齿同一竖直方向的永磁体充磁方向相同，同一初级齿上相邻永磁体的充磁方向相反.电枢绕组安装于半闭口槽内.电动机次级包括次级轭部和次级凸极，上下两侧的次级为轴对称结构，电动机初级和上下两侧的电动机次级之间均设有气隙.电动机内的磁场通过电动机初级和电动机上下两个次级形成串联闭合回路.

1.2 运行原理分析

DSLPPMV电动机结构上下对称，因此可基于半模型对电动机进行计算与分析，以减少分析和计算的复杂度.首先采用等效磁路法及磁场调制原理[9-10]对电动机的气隙磁通密度进行推导，以说明其运行原理.为了简化推导过程，假设如下：① 忽略漏磁；② 永磁体相对磁导率为1；③ 磁场仅在y方向变化；④ 铁心磁导率为无穷大.

由于NdFeB第二象限的退磁曲线近似为1条直线[4]，因此，永磁体可以等效成1个恒磁动势源FPM和1个恒定内磁导ΛPM串联的磁动势源，由以上4点假设，可以得到等效磁路模型.与此同时，次级磁导模型的傅里叶级数分解为

(1)

式中：Λ0为磁导中的直流分量;Λi为傅里叶系数；Ns为有效次级齿数；La为电动机初级长度;x为气隙位置；x0为次级初始位置.

此外，永磁体产生的磁动势FPM也可以使用傅里叶级数的形式表示为

(2)

式中：j=1,3,…,2n-1;Br为永磁体剩磁；hPM为永磁体厚度；μ0为真空磁导率；pPM为永磁磁场极对数；vc为初级运动速度.

仅考虑式(1)和式(2)的直流以及基波分量，DSLPPMV电动机的空载气隙磁密为

(3)

通过式(3)可以发现，空载气隙磁密Bag由3部分组成：第1部分由永磁体直接产生，由于电枢绕组和永磁体均位于初级，因此永磁体与电枢绕组的相对运动速度为0，所以气隙磁密的第1部分分量无法在电枢绕组中产生感应电势；第2、3部分气隙磁密分量均由初级永磁体所产生的磁场经由次级齿调制产生，因此，这2部分分量均与电枢绕组相对运动，故都能产生感应电动势，进而实现有效的机电能量转换.然而因第3部分的磁密运行速度快且波长长，因此可选其作为电动机的有效谐波分量.由式(3)分析可知，有效谐波磁通极对数pflux和运行速度vflux的关系满足：

pflux=|pPM-Ns|，

(4)

(5)

式中:Gr为有效谐波磁场速度和初级速度之比.

2 优化目标及敏感参数的选择

2.1 优化目标的选择

以电梯直接驱动系统为研究背景，即将DSLPPMV电动机动子直接安装于电梯轿厢，并驱动轿厢沿井道上下运动，因此，大推力特性是确保电梯的提升能力和上升加速度的首要特性.由于直线游标电动机本身推力脉动就比一般电动机小，而该直线电动机又呈对称结构，因此DSLPPMV电动机比传统单边直线游标电动机结构具有更小的推力脉动，其数值几乎可以忽略不计.因此，可以只选择电动机平均推力作为优化目标之一.

此外，高效率、低成本一直是电动机设计所追求的目标.电动机的损耗主要包括由电枢绕组引起的铜耗、由硅钢片引起的铁耗、由永磁体引起的涡流损耗和由摩擦引起的机械损耗以及附加损耗.其中，铁耗是由电动机铁心中磁场的不断变化而产生，受磁齿轮效应的影响，游标电动机气隙磁场的谐波含量往往十分丰富，导致铁耗在游标电动机的总损耗中所占比例较大，降低铁耗是有效改善游标电动机运行效率的有效手段之一，所以选择铁耗作为优化设计的第2个目标.

通过上述分析最终确定了2个优化目标，即平均推力和铁耗.

2.2 敏感参数的选择

一般来说，电动机结构参数对电动机性能均有着显著影响，且不同参数对电动机性能有不同的影响[11-14].当对电动机进行多目标优化设计时，相应的优化过程将会发展成1个高维问题.为了提高优化效率，在优化过程中引入了敏感度分析法，对各个尺寸参数对电动机各性能的影响程度进行评价，并按照不同影响程度将各尺寸参数划分为具有不同敏感等级的参数组.优化过程中，可仅对敏感度较高的参数进行优化，而保留敏感度指数很低参数的原始值，以有效降低电动机优化设计的维度，减少设计复杂度.为实施上述优化设计，首先对DSLPPMV电动机关键参数进行定义，如图2所示，其中: 初级总高度hc=76.00 mm；电动机总高度ha=198.00 mm；电动机有效长度La=680.00 mm；叠片长度Lz=200.00 mm；气隙长度g=3.00 mm；hPM=4.00 mm；永磁体宽度wm=18.00 mm；动子铁心间距wa=13.33 mm；槽高hb=25.00 mm；槽宽ws=38.00 mm；次级齿高ht=20.00 mm；次级轭高he=38.00 mm；次级极距τ=40.00 mm；齿宽Lt=齿根宽Lb=12.00 mm；槽满率sf=0.644.值得一提的是，考虑到次级齿根宽Lb对电动机性能的影响较小，为简化优化设计过程，所以取Lt=Lb.

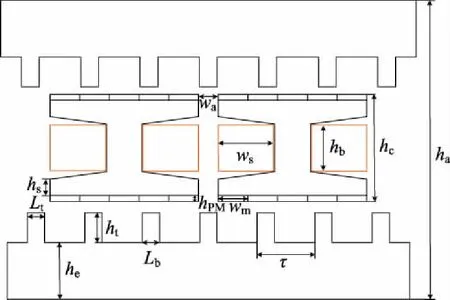
图2 电动机尺寸参数定义

由文献[15]可知,推力密度为

(6)

式中:B和J分别为电动机的磁负荷和电负荷；m为谐波次数.

由式(6)可以看出，电动机的推力与磁负荷和电负荷成正比，而电负荷与电枢电流成正比，所以电枢电流的改变对推力的影响巨大.通过改变初级齿高(同时改变槽高)可改变电枢的安匝数大小，此时推力也会随之变化.因此初级齿高(槽高)需要作为参数来优化.

根据上述分析以及传统电动机的设计经验，选择5个关键结构参数，分别是初级齿高hb、永磁体厚度hPM、永磁体宽度wm、次级齿高ht、次级齿宽Lt，其他参数则保持不变.将选定的结构参数做敏感度分析，如图3所示.

图3 参数敏感度指数图

从图3可以看出，单个参数对各目标影响程度各不相同，很难从全局的角度评价它们的影响.为了解决这一问题，也为了减少计算时间和保证较高的分析精度，因此选择采用计算综合敏感度指数来决定敏感参数分组.相应的灵敏度函数为

S(xi)=λ1HF(xi)+λ2Hloss(xi)，

(7)

式中：λ1和λ2分别为推力和铁耗的权重系数，且λ1、λ2满足方程λ1+λ2=1；HF(xi)和Hloss(xi)分别为推力和铁耗的敏感度指标的值.

表1 敏感度分析

为了提高优化效率，基于表1中列出的综合敏感度结果，参数可以分为2个级别，如表2所示.当|S(xi)|的值小于给定的阈值δ(取δ=0.1)时，认为是极其不敏感参数，可不予以优化；当|S(xi)|不小于阈值δ时，则认为是敏感参数，应着重优化.

表2 参数的敏感度等级

3 设计、仿真及分析

利用RSM建立适当的推力和损耗响应面模型时，通常采用二次近似模型来构造拟合响应面.响应面模型可以写成：

(8)

式中：Y为期望性能的RSM预测值；β0、βi、βii、βij为设计参数x(xi，xj)的回归系数；k为设计参数的数目；ε为随机误差，也称为统计误差.

从第2节的敏感度分析结果，可选定wm、Lt和hb这3个设计参数，由于永磁体、次级齿和初级齿都是呈对称结构，为了方便优化，以上述3个参数的1/2进行建模，即wm/2、Lt/2和hb/2.因此，在RSM中，wm1=wm/2、Lt1=Lt/2和hb1=hb/2是3个设计参数.

采用当前流行的中心组合设计(central compo-site design, CCD)来构造采样点.CCD由3部分组成：① 立方体点，其中因子水平被编码成-1和1；② 从中心点到距离为a的轴点；③ 1个设计中心点[16].各变量范围实际值的标准化值如表3所示，其中a=1.682.根据DSLPPMV电动机结构和3个高敏感度尺寸参数的设计范围，可以得到20个独立的RSM参数组合.

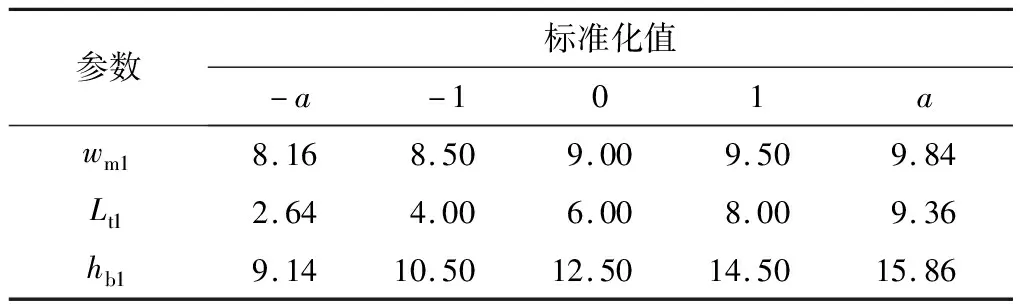
表3 各变量范围实际值的标准化值 mm

然后，建立上述20个参数组合相对应DSLPPMV电动机有限元模型，并进行求解，得出每个模型下的平均推力以及铁耗.根据CCD设计对模型设计变量的实际值进行标准化，设计变量实际值和编码值如表3所示.在每次试验中使用有限元法仿真出平均推力以及铁耗，结果如表4所示.

关系表示概念之间的相互联系，是从概念的外延方面来明确概念的。通过关系的作用，可以体现出概念由具体到抽象，由简单到复杂的发展过程，关系是概念之间的静态关联。概念网络设计了三种关系：父子关系、成员关系和概念场。父子关系就是逻辑学中概念的属种关系，即类与子类、类与分子的关系。种概念具有属概念的本质属性。因此，属概念与种概念之间具有相似性，正如父与子具有相似性一样。属概念是上位概念，种概念是下位概念，并且属种关系具有传递性。属种关系是一般与个别的关系。例如，动物，鸟，布谷鸟。布谷鸟具有鸟的本质属性，鸟具有动物的本质属性。

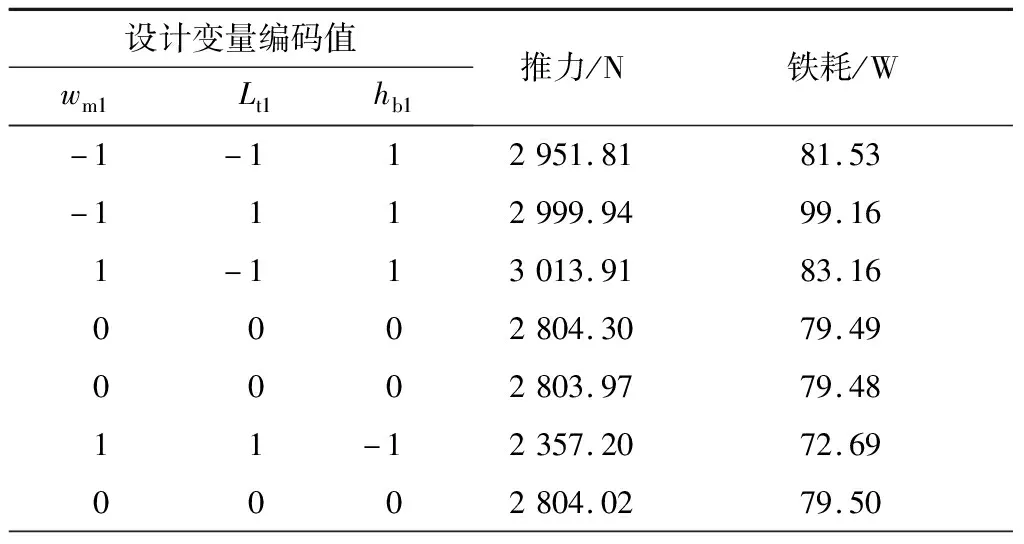
表4 CCD设计的仿真结果

利用20个独立模型的仿真结果和实际设计变量标准化后的编码值，拟合的推力以及铁耗的二阶回归模型为

F=-4 863.7+854.9wm1+97.572Lt1+346.82hb1-

(9)

loss=2.174 5+7.398 4wm1+2.700 72Lt1-

(10)

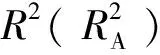
(11)

(12)

式(9)和(10)显示了电动机参数对推力以及铁耗的影响，具有表现形式直观和拟合精度高的优点，并能为电动机优化设计中优化目标的边界确定等工作提供极大的便利，因此，可以较容易地基于该模型进行电动机的设计优化.由回归模型可知，在wm1=8.16 mm，Lt1=2.64 mm，hb1=15.86 mm，即wm=16.32 mm，Lt=5.28 mm，hb=31.72 mm时得到1个最优点.由回归模型(9)和(10)得到的推力为2 958.33 N，铁耗为79.74 W.该参数下的推力不是最大，铁耗也不是最小，但却是在综合考虑到推力和铁耗这2个优化目标之间的平衡后，折中选择一个最优点，即最合理的设计方案之一.相比于原始参数时推力2 264.32 N和铁损76.51 W，推力增加了30.65%，铁损增加了4.22%.

4 DSLPPMV电动机测试

DSLPPMV电动机样机实物图如图4所示，样机主要包括支架，初级模块以及次级模块3部分组成，并通过在次级底板上安装的磁栅尺实现电动机动子位置的测量.

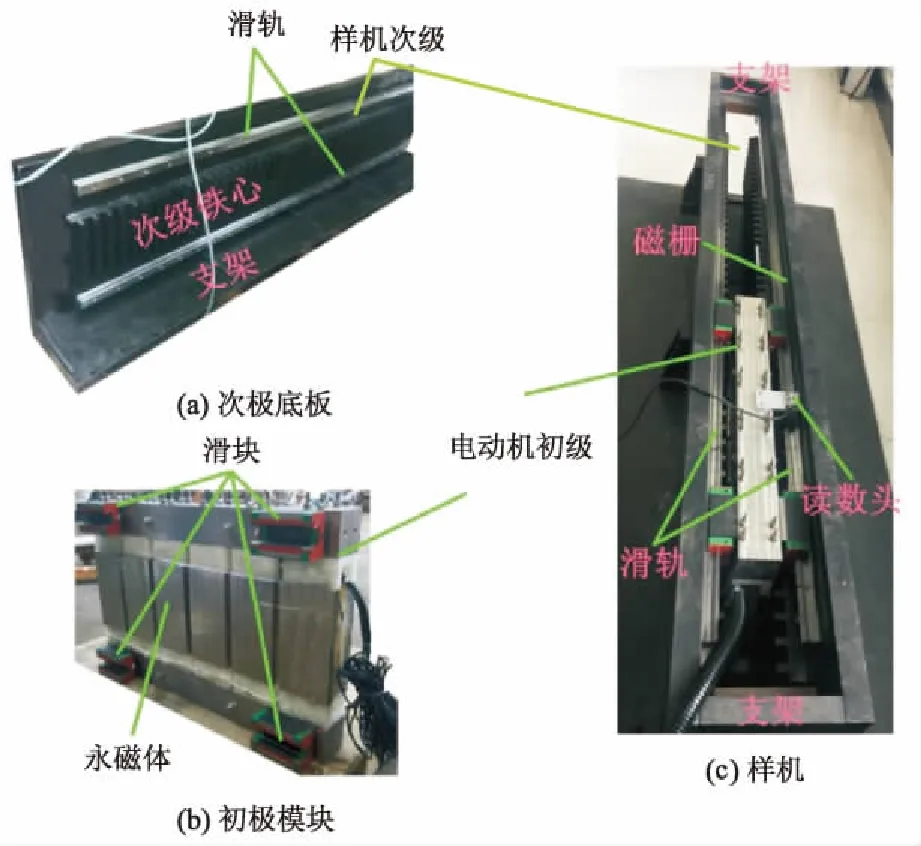
图4 DSLPPMV电动机样机

空载感应电动势实测和仿真波形如图5所示.图5a为DSLPPMV电动机运行速度为0.74 m·s-1时的实测空载感应电动势波形，峰值为67.5 V，为仿真值的96.0%，这是由于二维仿真中忽略了端部漏磁和加工误差等原因所致.

图5 三相空载感应电动势实测和仿真波形

为验证DSLPPMV电动机推力特性，对该电动机的静态推力进行了测试，即将动子通过拉压力传感器固定于某一位置，通过通入相应电流测量此位置时的电磁推力.由于该电动机的三相电感几乎不随动子位置发生变化[4]，因此采用id=0控制策略，即通入q轴电流.如图6所示，当电流比较小时，仿真值与实测值基本一致，且q轴电流与静态推力基本成正比.当电流大于9 A时，实测值逐渐小于仿真值.这是由于随着电流的不断增加，电动机推力也随之变大，使固定电动机动子的机械装置产生较大形变，从而导致动子位置与所施加电流的相位不符.当施加20 A电枢电流时，DSLPPMV电动机推力实测值为2 720 N，约为理论值的91.94%，验证了理论分析的有效性.