一种雷达数字收发机设计
2021-07-14倪文飞
倪文飞,夏 丹,崔 扬
(安徽四创电子股份有限公司,安徽 合肥 230000)
0 引言
数字收发机[1-2]的主要功能是处理模拟下变频通道输出的中频回波信号,同时为雷达设备提供中频激励信号。文献[3]提出了一种基于多通道技术的数字收发单元设计方法,文献[4]阐述了一种多通道高速数字收发设计,文献[5]通过直接数字式频率合成器(Direct Digital Synthesizer,DDS)实现信号合成。综上所述,传统模数转换器(Analog to digital converter,ADC)输出数据传输采用多路并行输出接口,当采样通道数及输出分辨率上升时,将会带来输出接口链路数上升、板级布线复杂等问题。同时DDS量化位数较低,需通过SPI总线模式对DDS内部各种繁琐的功能寄存器进行配置。针对以上问题,本文设计通过JESD204B串行输出接口[6]极大地缩减接口链路数,通过单对传输接口可实现16位量化数据传输,减小设计复杂度并优化电磁兼容等问题。采用国产DAC取代传统DDS,与DDS相比,数字模拟转换器(Digital to Analog Converter,DAC)具有量化位数高、信号可塑度强及逻辑控制简单等优点。
1 数字下变频
1.1 中频信号采样
ADC为国产4通道芯片,量化位数16 bit,采用JESD204B协议。中频输入信号频率为50 MHz且信号最大有效带宽为2 MHz,依据带通采样定理,理想情况下只需将采样频率大于2倍信号带宽即可,由于ADC为非线性器件,ADC工作时将产生谐波失真,因此采样频率过低将造成信号主谱与交调谱[7]难以区分,数字收发机原理框图如图1所示。
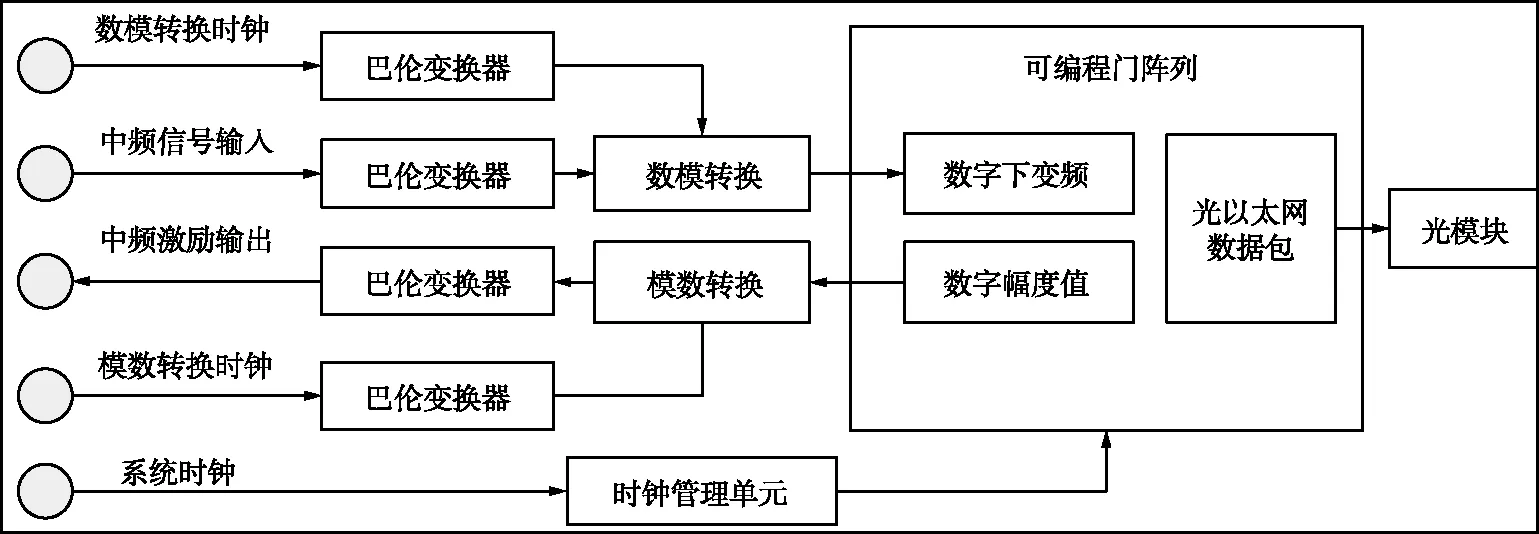
图1 数字收发机原理
以30 MS/s采样率对信号进行采样时,其主谱为10 MHz(60-50 MHz),二次谐波失真谱为10 MHz(100-90 MHz),因此二次谐波失真谱与主谱完全重叠。在选择ADC采样频率时可适当提高采样率以提升主谱识别度,即在可支持条件下尽可能扩展第一奈奎斯特频率区间。实际情况下ADC输出信号的频谱表达式为:
x(f)=xs(fo±fs)+a·xs(2fo±nfs)+
b·xs(3fo±mfs)+…,
(1)
式中,a,b分别为2次谐波失真(HD2)抑制值及3次谐波失真(HD3)抑制值。随着阶次的增加,失真抑制值同样将会逐步增大,一般只考虑2次及3次交调失真。
本文设计中,ADC以120 MS/s采样频率对中频信号进行采样,采样输出频谱分析如表1所示。

表1 ADC输出频谱分析
由表1可以看出,在第一奈奎斯特频率区间内,主谱与失真谱之间不存在交叠,其分布如图2所示。
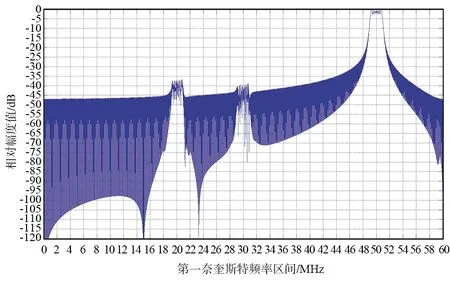
图2 ADC输出频谱
1.2 数字本振
ADC输出信号主谱频率在49~51 MHz,频率依然较高,需要通过数字混频将其转变为零中频信号,并通过滤波抽取以缩小数据率并节约传输带宽,数字下变频原理框图如图3所示。

图3 数字下变频原理
数字下变频[8]第一步是通过混频得到零中频信号,具体实现为:
(2)
(3)
(4)
(5)
(6)
数字本振的功能是产生2路数字混频信号,即式(3)中的nco_i与式(4)中的nco_q,输入信号xs分别与nco_i及nco_q进行相乘而得到初始的I、Q信号。数字本振的一种常用运算方法是利用多次迭代逼近算法实现,可以做到非常高的精度,是一种应用广泛的方法,但是需要占用较多的运算单元:
(7)
由于采样频率为120 MHz,信号中心频率为50 MHz,采样频率可整除信号中心频率,nco_i如式(7)所示,因此nco_i为一组循环数值,如表2所示。
由表2可以看出,I路混频信号只需通过一个12×18 bit的查找表实现,方法简单高效,Q路同理。
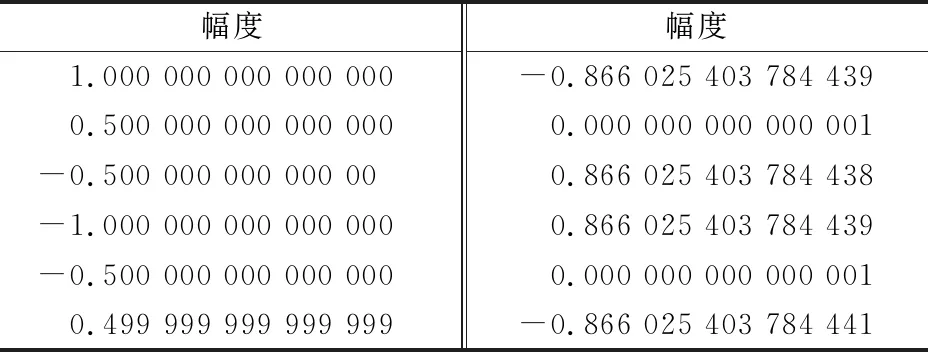
表2 nco_i循环数值
1.3 滤波抽取
信号经过混频将会输出和差信号,差信号便是零中频信号,需保留,其他信号需滤除。IQ最终采样频率为6 MS/s,满足原始信号带宽2 MHz的传输要求,由于原始采样频率为120 MS/s,因此DDC抽取因子为20。CIC[9]是一种高效滤波器,时域结构简单高效,可应用于第1级滤波抽取系统以降速并节约逻辑资源,如图4所示。

图4 CIC结构原理
由图4可知:
x′(n)=x′(n)Z-1+x(n)=x′(n-1)+x(n),
(8)
y(n)=x″(n)-x″(n)Z-1=x″(n)-x″(n-1)。
(9)
由上述表达式可知,CIC抽取滤波器可直接通过加减法实现,无需通过乘法器实现,可极大节约逻辑单元,同时其幅频响应表达式为:
(10)
由上述可知,阻带为12 MHz,远大于信号带宽,由于CIC阻带过大且旁瓣抑制依然不够,需采用第2级抽取滤波器以实现最终效果。滤波器设计是动态过程,大部分滤波函数均可实现所需滤波效果,第2级抽取滤波器采用FIR结构的inverse sinc低通滤波器实现,通带为0.8 MHz,阻带衰减为92 dB。
FIR滤波器的实现形式如下:
y(n)=x(n)*h(n)。
(11)
实际运算中,脉冲信号x(n)的有效长度是固定的,h(n)同样为固定长度脉冲序列,因此经过卷积运算后,y(n)的长度为:
length(y(n))=length(x(n))+length(h(n))-1。
(12)
FIR滤波器是直接通过乘法器实现,乘法运算将使输出结果位宽急速扩展,如果运算速率过大必须慎用乘法器,以免产生时序违例。但是由于信号先经过CIC滤波抽取处理,信号采样率已经降低为12 MS/s,因此信号与脉冲响应序列进行乘积时,可尽量避免时序违例,运算中的建立时间及保持时间[10]也可满足,运算可有序进行。同时由式(12)可知,经过卷积运算后,脉冲序列必定出现时宽失真,因此在进行FIR滤波器设计时,必须尽可能减少冲击响应阶数,灵活选择滤波窗函数。
本文设计中,滤波抽取的思路是先通过灵活高效的CIC抽取滤波器进行降速,而后通过FIR滤波器优化阻带及阻带衰减值。IQ实测频谱图如图5所示。由图5可知,除主谱外,不存在其他干扰。
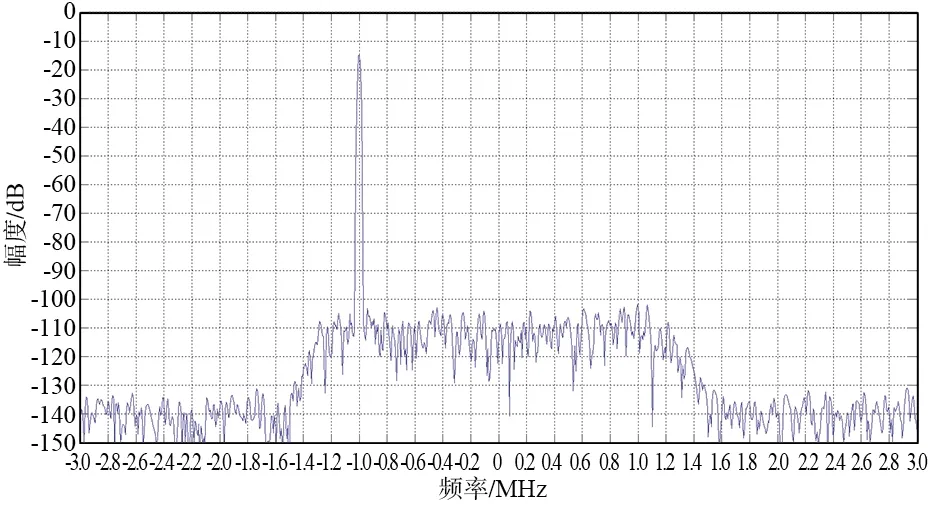
图5 数字下变频IQ输出频谱
2 信号合成
由于信号最高频率为51 MHz,以奈奎斯特采样定理为依据,理想采样频率为102 MHz。为了提高DAC输出信号质量,一般将输出信号频率控制在采样频率40%以内,采用该准则的一个主要原因是DAC输出信号的功率是滚降的,即随着输出信号频率的上升,其对应输出功率将会下降,其次与ADC同理,通过增大第一奈奎斯特频率区间以提高信号分辨度。因此采用240 MHz时钟作为DAC参考频率:
(13)
式(13)是在单重复周期内,输出信号的数学表达式。信号产生的具体过程为在FPGA通过CORDIC算法[11-12]得出数字幅度值,然后DAC芯片依据所接收数字幅度值直接输出模拟信号。CORDIC算法依据数字相位值而产生数字幅度值,由表达式可知,在调频时间内,归一化相位值为:
(14)
式中,fo为49 MHz;fs为240 MHz;B为调频带宽2 MHz;To为调频时间40 μs;n为调频离散时间间隔。
对于DAC而言,改善因子是重要参数,在重复周期T内,脉冲是功率信号,信号功率表达式为:
(15)
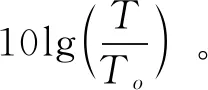
(16)
式中,N为连续波噪声谱密度实测值。
改善因子对比如图6所示。

图6 改善因子对比
3 结束语
本文设计利用国产芯片实现,通过合适的采样方案节约系统逻辑资源,同时分析及阐述了进行数字收发软硬件设计所涉及原则及注意事项,可以将该设计应用到大多数中频收发方案中。
目前模数转换及数模变换均朝着高采样率及多通道集成的方向发展,DAC芯片可直接输出X波段信号,ADC采样带宽也完全可覆盖到C波段。对于传统雷达整机而言,已经面临颠覆性变化,即设备量极大缩减及设备小型化。如今国产芯片正迎头赶上,在不同波段应用领域具有优良应用,不远的将来必将比肩国外。
