基于近似模型某水库帷幕灌浆优化设计研究

李栋梁，杨 慧，贺 苗，王 蒙

(徐州市水利建筑设计研究院， 江苏 徐州 221000)

水库渗流问题是影响水库使用的重要因素，水库渗流严重可导致工程效益降低，甚至出现安全风险。在水库防渗工程中，常用的手段是防渗帷幕，但是，防渗帷幕设计缺少相关规范，设计方法多种多样。目前，防渗帷幕主要是从形态方面进行分析，因此，从形态方面考虑对防渗帷幕设计进行优化。目前，有限元数值模拟方法在防渗帷幕设计中得到了较为广泛的应用，计算速度较高，结果较为可靠[1-3]。然而为了使得防渗帷幕方案达到最优，需要构建多组数值模拟模型，这就加大了设计人员的工作量，降低帷幕设计效率。近似模型是一种利用数学表达式代替数值模拟模型的方法，通过多种数值模拟，建立变量与输出结果之间的关系，之后，利用相关算法获取关系式的最优结果，从而获取最优方案。目前，近似模型在水利工程中得到了较为广泛的使用[4-5]。较为常用的最优值算法包括：遗传算法、粒子群算法、蝙蝠算法等[6-10]。

以某水库坝址区防渗帷幕优化设计工程为实例进行研究分析。水库主要承担防洪、蓄水、灌溉、发电等综合功能。水库设计采用土工膜斜墙坝，初步设计大坝长132.05m，坝高10～15.75m，坝顶宽度4.5m。根据调查，坝址区岩土体结构发育，渗透性较强，需采取相关防渗措施。

1 近似模型基本原理

近似模型主要依据数学的基本原理，任意的函数均可以以多项式的形式进行表达。同时，精度可满足相关设计要求。在进行不确定性分析的研究中，可采用随机展开方式表达计算过程中到的概率统计结果。

近似模型基本原理如下：

z为空间Ω内的不确定模型，计算公式为：

z=Z(x，t)

(1)

式中，x—空间Ω内不确定因素取值，由N组独立变量组成：x=(x1，x2，…，xN)T。

设变量i边缘概率密度为：fi(xi)，则联合概率为：f(x)=f1(x1)f2(x2)…fN(xN)。

式(1)以多项式展开为：

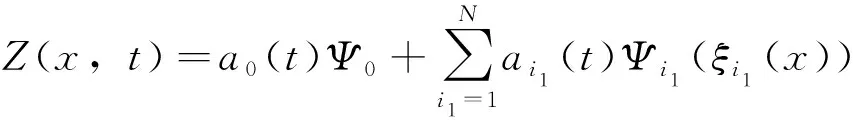
(2)

对式(2)进行简化：

(3)

式中，ξ—满足随机分布的变量；a—确定性系数；Φ—P阶多项式。

多项式展开时，基函数满足正交关系：

(4)

式中，E—数学期望；δ—Kronecher算式。

(5)

前P阶多项式为：

(6)

保留P阶多项式为：

(7)

所有项展开式为：

ai(t)=E[Z(x，t)Φi(ξ)]

(8)

利用混沌系数求各阶矩，计算方法如下：

E[z′(x，t)]=a0

(9)

(10)

使用高斯投影法分配混沌系数：

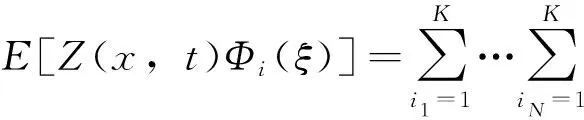
(11)

式中，ξi1—所有变量高斯积分点；ωiN—各变量权重。

2 建立防渗帷幕优化设计近似模型

根据工程经验结合理论分析，防渗帷幕主要受到上覆大坝坝体的自重压力、上下游水压力以及防渗帷幕自身重力。根据初步设计成果和水库勘察成果，水库大坝坝体、坝基以及防渗帷幕材料计算参数见表1。

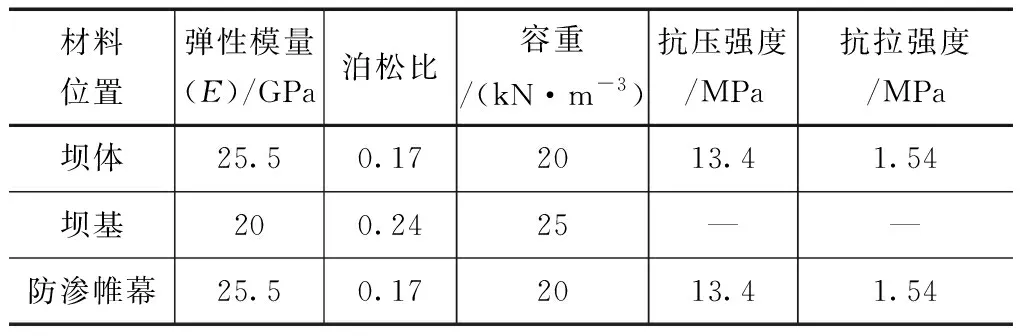
表1 各处材料强度参数

2.1 样本数据选取

近似模型样本点选取对模型精度以及收敛速度有较大的影响。目前，在样本点抽取中常用的方法为Latin hypercube sampling(LHS)法。使用该方法抽取的样本数据具备足够的代表性，同时，人为因素影响较低，以该方法抽取的数据，可实现计算模型的快速收敛。样本点抽取数量需满足以下要求。假设计算变量总数为n，则样本点数量需不少于(n+1)(n+2)/2个。从防渗帷幕形态方面考虑优化设计防渗方案，可从防渗帷幕长、宽、深3个维度进行考虑，因此设计变量为3个，因此，样本点抽取数量不应少于10个。综合考虑，为了计算模型的计算精度，采用LHS法随机选取35组样本数据建立模型，并选取15组数据检验近似模型的计算精度。

2.2 基于L—D—H的防渗帷幕设计近似模型构建

从形态方面考虑，帷幕参数主要由长(L)、宽(D)、深(H)3个变量控制。数值模拟计算选取ANSYS软件，该软件模型建立简单、计算结果准确、接口多，在工程实践中得到了广泛的使用[10-15]。模型建立步骤如下：①根据水库实际情况，建立ANSYS数值模拟模型。②建立多组数值模拟实验。③利用MATLAB软件提取ANSYS数值模拟结果，获取样本数据。④建立关于L-D-H和渗流结果(水力坡降和渗流量)的浸塑模型，利用下式对近似模型的计算精度进行检查，数值越小计算精度越高。

δ1=Max{|fi-f|}(i=1，…，N)

(12)

(13)

式中，δ1、δ2—最大、均方根误差；N—检测点总数。

精度检测结果见表2。

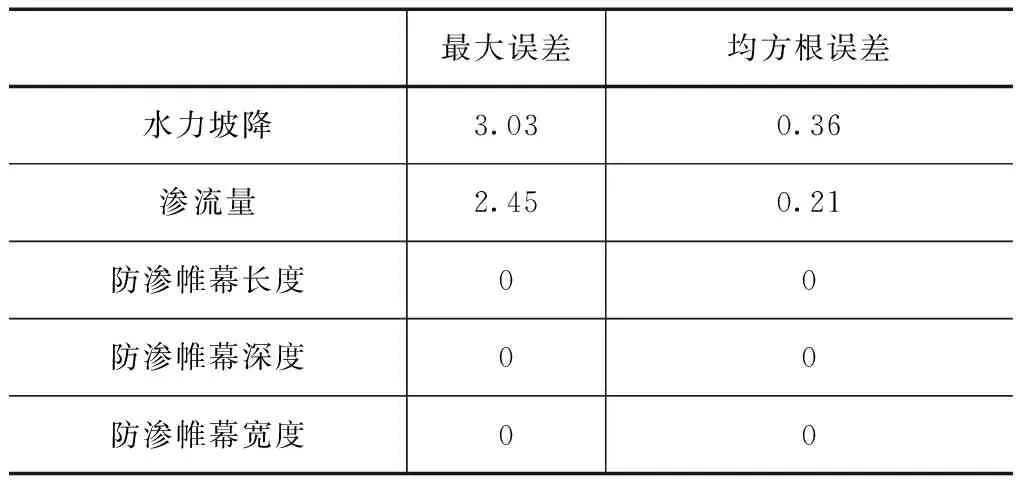
表2 近似模型精度评价结果 单位：%

由表2中的精度检测结果可知，所建立的近似模型计算精度较高，可以满足防渗帷幕优化设计要求，其中水力坡降最大误差为3.03%，均方根误差为0.36%；渗流量最大误差为2.45%，均方根误差为0.21%。因此，可使用建立的近似模型代替ANSYS数值模拟进行水库防渗帷幕优化设计工作。

3 改进粒子群算法

粒子群算法是一种极为常用的最优值算法，基础的粒子群算法易出现计算结果为范围最优值的情况，导致计算结果出现偏差。为了改善这一情况，提出使用交叉因子和动态惯性因子改善基础粒子群算法，从而获取全局最优值。

为避免基础粒子群算法出现局部最优值，引入交叉因子、学习因子和动态惯性因子改进粒子群算法。

3.1 交叉因子

引入交叉因子可获取某粒子i在t时刻的位置Xi，t=1，将位置Xi，t=1与粒子最优位置交叉计算，生成离散的位置Qi，t={qi，t1，qi，t2，…，qi，tD}，计算公式为：

(14)

式中，randj(0，1)—在[0，1]范围的随机数；jrand—[1，D]范围随机整数；p—粒子间交叉的概率。

不断更新粒子最优位置：

(15)

式中，pbestti，t+1j—更新前粒子最优位置；f—自适应函数。

3.2 动态惯性因子

动态惯性因子为粒子进化度和聚合度，计算公式为：

(16)

式中，m、n—粒子进化度、聚合度；Pg，i、Pg，i-1—当前、上一时刻的全局最优值；Ps—粒子群总数。

惯性权重计算公式为：

ω=f(m，l)=ω0-0.6m+0.15n

(17)

式中，ω0—初始惯性权重。

4 防渗帷幕优化设计

4.1 设计变量的选取

采用向量形式表示防渗帷幕设计变量，X=[L，D，H]。

4.2 变量约束条件

X1=[133，10，20]；X2=[180，40， 40]；

I≤1.5；Q≤10L/s

(18)

式中，X1、X2—计算变量的下限、上限；I—水力坡降；Q—渗流量，L/s。

4.3 防渗帷幕优化设计结果

基于改进粒子群算法—近似模型计算，获取最优的防渗帷幕设计方案，见表3。

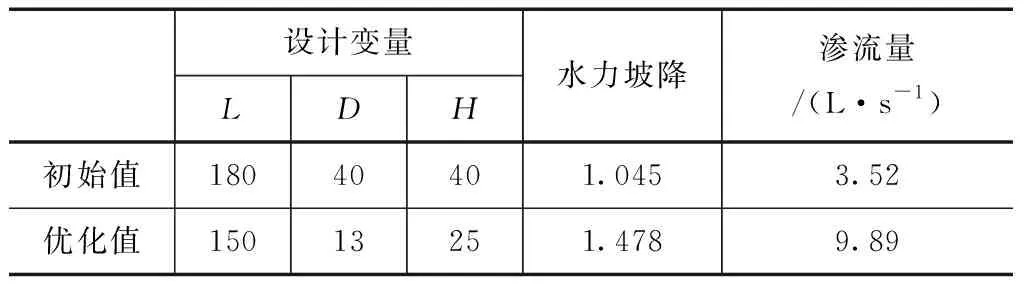
表3 优化设计前后各变量参数

4.4 防渗帷幕优化设计工程效果

从表3可知，经优化设计后，帷幕灌浆量大大减小，水力坡降从1.045变为1.478，渗流量从3.52L/s变为9.89L/s，满足工程要求。利用ANSYS验算优化后的帷幕方案，计算得到渗流量为9.97L/s，两者计算结果基本一致。

5 结论

为了降低某水库防渗帷幕优化设计中数值模拟模型计算量，提出使用近似模型代替数值模拟模型。通过LDS方法抽取样本数据建立近似模型，通过检验近似模型精度较高，可满足设计要求。通过改进粒子群算法获取近似模型最优值，从而获取优化设计后的防渗帷幕规模。通过对比分析，防渗帷幕灌浆量与初始计算值相比大大减小，水力坡降以及渗流量亦可满足相关要求。